از ویکیپدیا، دانشنامه آزاد

 

این مقاله در مورد بخش خط است. برای استخوان، شعاع (استخوان) را ببینید. برای کاربردهای دیگر، شعاع (ابهام‌زدایی) را ببینید .

دایره با محیط C به رنگ سیاه، قطر D به رنگ آبی، شعاع R به رنگ قرمز، و مرکز یا مبدا O به رنگ سبز.

در هندسه کلاسیک ، شعاع دایره یا کره هر یک از پاره خط ها از مرکز آن تا محیط آن است و در استفاده مدرن تر، طول آنها نیز می باشد. این نام از کلمه لاتین radius گرفته شده است که به معنای پرتو و همچنین پره چرخ ارابه است. [1] جمع شعاع می تواند شعاع (از جمع لاتین) یا شعاع جمع انگلیسی معمولی باشد. [2] مخفف معمولی و نام متغیر ریاضی شعاع R یا r است. با گسترش، قطر D به عنوان دو برابر شعاع تعریف می شود: [3]

{\displaystyle d\doteq 2r\quad \Rightarrow \quad r={\frac {d}{2}}.}

اگر جسمی مرکز نداشته باشد، این اصطلاح ممکن است به شعاع محیطی ، شعاع دایره محدود یا کره محصور آن اشاره کند. در هر صورت، شعاع ممکن است بیش از نصف قطر باشد، که معمولاً به عنوان حداکثر فاصله بین هر دو نقطه از شکل تعریف می شود. شعاع یک شکل هندسی معمولاً شعاع بزرگترین دایره یا کره موجود در آن است. شعاع داخلی یک حلقه، لوله یا دیگر جسم توخالی، شعاع حفره آن است.

برای چند ضلعی های منظم ، شعاع همان شعاع محیطی آن است. [4] شعاع چند ضلعی منتظم را آپوتم نیز می‌گویند . در تئوری گراف ، شعاع یک گراف حداقل در تمام رئوس u حداکثر فاصله از u تا هر رأس دیگر گراف است. [5]

شعاع دایره با محیط ( محیط ) C برابر است

{\displaystyle r={\frac {C}{2\pi }}}

 

فهرست

فرمول [ ویرایش ]

برای بسیاری از اشکال هندسی، شعاع رابطه کاملاً مشخصی با سایر معیارهای شکل دارد.

حلقه ها [ ویرایش ]

همچنین ببینید: مساحت دایره

شعاع دایره ای با مساحت A برابر است

{\displaystyle r={\sqrt {\frac {A}{\pi }}}.}

شعاع دایره ای که از سه نقطه غیر خطی P 1 , P 2 , P 3 می گذرد با

{\displaystyle r={\frac {|{\vec {OP_{1}}}-{\vec {OP_{3}}}|}{2\sin \theta }},}

که در آن θ زاویه

 ∠ P 1 P 2 P 3

 است. این فرمول از قانون سینوس ها استفاده می کند . اگر سه نقطه با مختصات آنها ( x 1 , y 1 ) , ( x 2 , y 2 ) و ( x 3 , y 3 ) داده شوند، شعاع را می توان به صورت بیان کرد.

{\displaystyle r={\frac {\sqrt {[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}][(x_{2) }-x_{3})^{2}+(y_{2}-y_{3})^{2}][(x_{3}-x_{1})^{2}+(y_{3} -y_{1})^{2}]}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3 }-x_{2}y_{1}-x_{3}y_{2}|}}.}

چند ضلعی های منظم [ ویرایش ]

همچنین ببینید: دایره محدود

nR n
30.577 350...
40.707 106...
50.850 650...
61.0
71.152 382...
81.306 562...
91.461 902...
101.618 033...

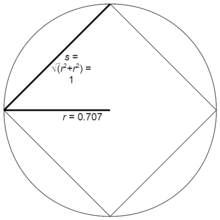
برای مثال یک مربع ( n =4)

شعاع r یک چندضلعی منتظم با n ضلع به طول s با r = R n s به دست می آید که در آن{\displaystyle R_{n}=1\left/\left(2\sin {\frac {\pi }{n}}\right)\right..} مقادیر R n برای مقادیر کوچک n در جدول آورده شده است. اگر s = 1 باشد، این مقادیر نیز شعاع چند ضلعی های منظم مربوطه هستند.

 

هایپرمکعب [ ویرایش ]

شعاع یک ابر مکعب d بعدی با ضلع s است

r={\frac {s}{2}}{\sqrt {d}}.

استفاده در سیستم های مختصات [ ویرایش ]

مختصات قطبی [ ویرایش ]

نوشتار اصلی: سیستم مختصات قطبی

سیستم مختصات قطبی یک سیستم مختصات دو بعدی است که در آن هر نقطه از یک صفحه با فاصله از یک نقطه ثابت و یک زاویه از یک جهت ثابت تعیین می شود.

نقطه ثابت (مشابه با مبدأ سیستم دکارتی ) قطب نامیده می شود و پرتوی از قطب در جهت ثابت محور قطبی است . فاصله از قطب را مختصات شعاعی یا شعاع می گویند و زاویه را مختصات زاویه ای ، زاویه قطبی یا آزیموت می نامند . [6]

مختصات استوانه ای [ ویرایش ]

نوشتار اصلی: سیستم مختصات استوانه‌ای

در سیستم مختصات استوانه ای، یک محور مرجع انتخابی و یک صفحه مرجع انتخابی عمود بر آن محور وجود دارد. مبدأ سیستم نقطه‌ای است که هر سه مختصات را می‌توان صفر داد. این محل تقاطع بین صفحه مرجع و محور است.

این محور را به‌طور متفاوتی محور استوانه‌ای یا طولی می‌نامند تا آن را از محور قطبی متمایز کند ، که پرتویی است که در صفحه مرجع قرار دارد و از مبدا شروع می‌شود و در جهت مرجع قرار می‌گیرد.

فاصله از محور ممکن است فاصله شعاعی یا شعاع نامیده شود ، در حالی که مختصات زاویه ای گاهی اوقات به عنوان موقعیت زاویه ای یا به عنوان آزیموت نامیده می شود . شعاع و آزیموت با هم مختصات قطبی نامیده می شوند ، زیرا با یک سیستم مختصات قطبی دوبعدی در صفحه از طریق نقطه، موازی با صفحه مرجع مطابقت دارند. مختصات سوم ممکن است ارتفاع یا ارتفاع (اگر صفحه مرجع افقی در نظر گرفته شود)، موقعیت طولی ، [7] یا موقعیت محوری نامیده می شود . [8]

مختصات کروی [ ویرایش ]

نوشتار اصلی: سیستم مختصات کروی

در یک سیستم مختصات کروی، شعاع فاصله یک نقطه از یک مبدأ ثابت را توصیف می کند. موقعیت آن اگر بیشتر با زاویه قطبی اندازه گیری شده بین جهت شعاعی و جهت اوج ثابت، و زاویه آزیموت، زاویه بین برآمدگی متعامد جهت شعاعی بر روی صفحه مرجعی که از مبدا می گذرد و متعامد به نقطه اوج است، تعریف شود. و یک جهت مرجع ثابت در آن صفحه.

همچنین مشاهده کنید [ ویرایش ]

منبع 

https://en.wikipedia.org/wiki/Radius