می‌توانیم این سری‌ها را طوری ضرب کنیم که انگار سری‌های متناهی هستند. ما ضرایب را جمع آوری می کنیم:

  • جمله ثابت 1 است .

  • ترم درجه اول 1 + 1 = 2 است.

  • ترم درجه دوم 1 + 1 + 1/2 = 5/2 است.

  • ترم درجه سوم 1 + 1 + 1/2 + 1/6 = 8/3 است

  • ترم درجه چهارم 1 + 1 + 1/2 + 1/6 + 1/24 = 65/24 است.

ما می‌توانیم این فرآیند را به‌طور نامحدود ادامه دهیم، یا بهتر است از رایانه برای تولید شرایط استفاده کنیم.

سریال است

                      5 8 65
        1 + x +        x 2   +         x 3   +            x 4   + ...
                      2 3 24     
 

 

تقسیم بندی سری های قدرت

فرض کنید می‌خواهیم نمایش سری توانی را  در مخرج ضرب کنیم و ضرایب را برابر کنیم:         (c 0 + c 1 x + c 2 x 2 + ...)(1 + x + x 2 /2 + x 3 /6 + x 4 /24 + ...) = (x - x 3 /3 + x 5 /5- x 7/7 + ...)

        


 

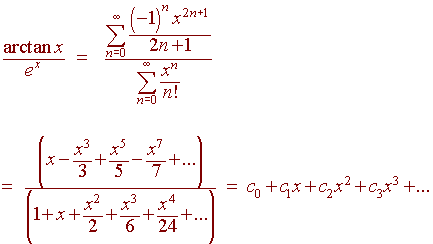
  • ضریب ثابت به ما  c 0 = 0 می دهد .

  • عبارت درجه اول به ما c 0 + c 1 = 1 می دهد. بنابراین c 1 = 1 .

  • جمله درجه دوم 1 + c 2 = 0 به ما می دهد . بنابراین c 2 = -1 .

  • عبارت درجه سوم 1/2 - 1 + c 3 = -1/3 به ما می دهد . بنابراین c 3 = 1 - 1/2 - 1/3 = 1/6 .

و غیره  

منبع

https://ltcconline.net/greenl/courses/107/Series/taylrser.htm