ریاضیات

از آنجا که

انتگرال آن دارای نمایش سری قدرت است

بیایید حد نسبت های مطلق این سری را پیدا کنیم:

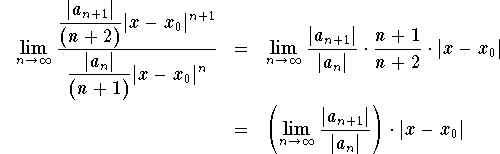
اما توجه داشته باشید که این دقیقاً همان عبارتی است که هنگام محاسبه حد نسبتهای مطلق سری تیلور از f ( x ) به آن برخورد می کنیم. بنابراین هر دو سری شعاع همگرایی یکسانی دارند!

سری تیلور و چند جمله ای ها

سری تیلور چند جمله ای چیست؟

سری تیلور با مرکز  یک چند جمله ای خود چند جمله ای است! (این را با چند جمله ای مورد علاقه خود بررسی کنید و از فرمول سری تیلور با مرکز استفاده کنید!)

اگر مرکز 0 نباشد چه؟ سپس شخص واقعاً چند جمله ای را بازنویسی می کند و  به جای استفاده از آن  به عنوان "بلوک های سازنده" آن استفاده می کند.

در اینجا یک مثال آورده شده است: سری تیلور را با مرکز  چند جمله ای پیدا کنید. بیایید مشتقات آن را بگیریم و وصل کنیم :

بنابراین p (-1)=1+3+5=9.

p '( x )=2 x -3، بنابراین p '(-1)=-2-3=-5.

p ''( x )=2، بنابراین p ''(-1)=2.

تمام مشتقات بالاتر 0 هستند، بنابراین سری تیلور خاتمه می یابد!

با استفاده از فرمول ما به دست می آوریم:

از این رو، فهمیدن اینکه یک تابع دارای سری پایانی تیلور است، سخت نیست، اگر و فقط اگر تابع چند جمله ای باشد.

ضرب سری تیلور در چند جمله ای

بیایید سعی کنیم بسط سری تیلور  با مرکز را پیدا کنیم .

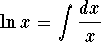برای پیدا کردن سری تیلور برای ، از آن استفاده کنید . شما بسط را بدست می آورید:

همانطور که در مثال بالا می توانیم بازنویسی کنیم

سپس هر دو عبارت را ضرب می کنیم:

بدون وارد شدن به جزئیات فنی: اگر اولین عبارت های این سری را بنویسید، می توانید قدرت های مربوط به ( x -1) را با هم ترکیب کنید تا شروع سری تیلور را برای f ( x ) بدست آورید:

خودت آن را امتحان کن!

تقریباً چندان پیچیده نیست: نمایش سری تیلور را با مرکز  برای پیدا کنید.

منبع

http://www.sosmath.com/calculus/tayser/tayser05/tayser05.html