اثر داپلر نسبیتی برای صدا و نور
[ ویرایش ]
شکل 10. فرمول تغییر داپلر نسبیتی هم برای صوت و هم برای نور قابل استفاده است.
کتابهای درسی فیزیک سال اول تقریباً همیشه تغییر داپلر را برای صوت بر حسب سینماتیک نیوتنی تجزیه و تحلیل میکنند، در حالی که تغییر داپلر برای نور و پدیدههای الکترومغناطیسی را از نظر سینماتیک نسبیتی تحلیل میکنند. این تصور نادرست را ایجاد می کند که پدیده های صوتی نیاز به تحلیل متفاوتی نسبت به نور و امواج رادیویی دارند.
تجزیه و تحلیل سنتی اثر داپلر برای صدا نشان دهنده یک تقریب سرعت پایین به تجزیه و تحلیل دقیق و نسبیتی است. آنالیز کاملا نسبیتی صوت در واقع به همان اندازه برای پدیده های صوت و الکترومغناطیسی قابل استفاده است.
نمودار فضازمان را در شکل 10 در نظر بگیرید. خطوط جهانی برای یک چنگال تنظیم (منبع) و یک گیرنده هر دو در این نمودار نشان داده شده اند. چنگال تنظیم و گیرنده از O شروع می شود، در این نقطه، چنگال تنظیم شروع به ارتعاش می کند، امواج منتشر می کند و در امتداد محور منفی x حرکت می کند در حالی که گیرنده شروع به حرکت در امتداد محور x مثبت می کند. چنگال تنظیم تا رسیدن به A ادامه مییابد، در این مرحله امواج را متوقف میکند: بنابراین یک بسته موج تولید شده است و تمام امواج در بسته موج توسط گیرنده دریافت میشود و آخرین موج به آن در B میرسد. زمان مناسب برای مدت زمان بسته در چارچوب مرجع چنگال تنظیم طول OA است در حالی که زمان مناسب برای مدت زمان بسته موج در چارچوب گیرنده مرجع طول OB است. اگرn








معادله 9:
اگر


اگر سرعت انتشار سیگنال 



تجزیه و تحلیل نمودار فضازمان در شکل 10 فرمولی کلی برای حرکت منبع و گیرنده به طور مستقیم در امتداد خط دید خود، یعنی در حرکت خطی به دست داد.
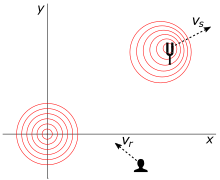
شکل 11. یک منبع و گیرنده در جهات و سرعت های مختلف در یک قاب حرکت می کنند که سرعت صوت مستقل از جهت است.
شکل 11 یک سناریو را در دو بعد نشان می دهد. منبع با سرعت حرکت می کند



نسبت بین فرکانس های مناسب برای منبع و گیرنده است
نسبت پیشرو به شکل اثر داپلر کلاسیک است، در حالی که عبارت جذری نشان دهنده تصحیح نسبیتی است. اگر زوایا را نسبت به قاب منبع در نظر بگیریم، پس






 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.