نسبیت خاص
خط جهان: نمایش نموداری فضازمان
نشان می دهد

پایه ها

نشان می دهد

عواقب

نشان می دهد

فضا-زمان

نشان می دهد

دینامیک

نشان می دهد
نشان می دهد

مردم

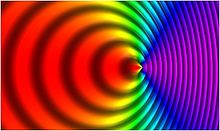
شکل 1. منبعی از امواج نوری که به سمت راست حرکت می کنند، نسبت به ناظران، با سرعت 0.7 c . فرکانس برای ناظران سمت راست بیشتر و برای ناظران سمت چپ کمتر است.

اثر نسبیتی داپلر تغییر در فرکانس ، طول موج و دامنه [ 1 ] نور است که ناشی از حرکت نسبی منبع و ناظر است (مانند اثر داپلر کلاسیک ، اولین بار توسط کریستین داپلر در سال 1842 [ 2 ] ارائه شد ). هنگام در نظر گرفتن اثرات توصیف شده توسط نظریه نسبیت خاص .

اثر داپلر نسبیتی با اثر داپلر غیر نسبیتی متفاوت است زیرا معادلات شامل اثر اتساع زمانی نسبیت خاص است و محیط انتشار را به عنوان نقطه مرجع در بر نمی گیرد. آنها تفاوت کل در فرکانس های مشاهده شده را توصیف می کنند و دارای تقارن لورنتس مورد نیاز هستند .

اخترشناسان سه منبع انتقال به سرخ / آبی را می شناسند : جابجایی داپلر. جابجایی های قرمز گرانشی (به دلیل خروج نور از میدان گرانشی)؛ و گسترش کیهانی (جایی که خود فضا امتداد می یابد). این مقاله فقط به تغییرات داپلر مربوط می شود.

خلاصه نتایج عمده

[ ویرایش ]

در جدول زیر فرض شده است که برای{\displaystyle \beta =v/c>0}گیرنده{\displaystyle r}و منبع {\displaystyle s}از یکدیگر دور می شوند،{\displaystyle v}سرعت نسبی و{\displaystyle c}سرعت نور و{\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}}.

سناریوفرمولیادداشت ها

اثر داپلر طولی نسبیتی		{\displaystyle {\frac {\lambda _{r}}{\lambda _{s}}}={\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+ \بتا {1-\بتا }}}}
اثر داپلر عرضی،
نزدیکترین رویکرد هندسی		{\displaystyle f_{r}=\گاما f_{s}}Blueshift
اثر داپلر عرضی،
نزدیکترین رویکرد بصری		{\displaystyle f_{r}={\frac {f_{s}}{\gamma }}}انتقال به قرمز
TDE، گیرنده در
حرکت دایره ای در اطراف منبع		{\displaystyle f_{r}=\گاما f_{s}}Blueshift
TDE، منبع در
حرکت دایره ای اطراف گیرنده		{\displaystyle f_{r}={\frac {f_{s}}{\gamma }}}انتقال به قرمز
TDE، منبع و گیرنده
در حرکت دایره ای در اطراف
مرکز مشترک		{\displaystyle {\frac {f'}{f}}=\left({\frac {c^{2}-R^{2}\omega ^{2}}{c^{2}-R'^ {2}\omega ^{2}}}\right)^{1/2}}بدون تغییر داپلر
زمانی که "{\displaystyle R=R'}
حرکت در جهت دلخواه
در قاب گیرنده اندازه گیری می شود		{\displaystyle f_{r}={\frac {f_{s}}{\gamma \left(1+\beta \cos \theta _{r}\right)}}}
حرکت در جهت دلخواه
در قاب منبع اندازه گیری می شود		{\displaystyle f_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)f_{s}}

اشتقاق

[ ویرایش ]

اثر داپلر طولی نسبیتی

[ ویرایش ]

تغییر داپلر نسبیتی برای حالت طولی، با منبع و گیرنده در حال حرکت مستقیم به سمت یا دور از یکدیگر، اغلب به عنوان پدیده کلاسیک مشتق می‌شود، اما با افزودن عبارت اتساع زمانی اصلاح می‌شود . [ 3 ] [ 4 ] این رویکردی است که در کتاب‌های درسی فیزیک یا مکانیک سال اول مانند کتاب‌های فاینمن [ 5 ] یا مورین استفاده می‌شود. [ 6 ]

به دنبال این رویکرد برای استخراج اثر داپلر طولی نسبیتی، فرض کنید گیرنده و منبع با سرعت نسبی از یکدیگر دور می شوند.v{\displaystyle v\,}همانطور که توسط یک ناظر بر روی گیرنده یا منبع اندازه گیری می شود (قرارداد نشانه ای که در اینجا به تصویب رسید این استv{\displaystyle v\,}اگر گیرنده و منبع به سمت یکدیگر حرکت کنند منفی است ).

مشکل را در چارچوب مرجع منبع در نظر بگیرید.

فرض کنید یک جبهه موج به گیرنده برسد. جبهه موج بعدی در یک فاصله است{\displaystyle \lambda _{s}=c/f_{s}\,}دور از گیرنده (جایی که{\displaystyle \lambda _{s}\,}طول موج است ،{\displaystyle f_{s}\,}فرکانس امواجی است که منبع ساطع می کند و{\displaystyle c\,}سرعت نور است ).

جبهه موج با سرعت حرکت می کند{\displaystyle c\,}، اما در عین حال گیرنده با سرعت دور می شود{\displaystyle v}در طول یک زمان {\displaystyle t_{r,s}}، که دوره برخورد امواج نور به گیرنده است، همانطور که در قاب منبع مشاهده می شود. بنابراین،

{\displaystyle \lambda _{s}+vt_{r,s}=ct_{r,s}\Longleftrightarrow \lambda _{s}=ct_{r,s}(1-v/c)\longftrightarrow t_{r ,s}={\frac {1}{f_{s}(1-\beta )}},}

که{\displaystyle \beta =v/c\,}سرعت گیرنده بر حسب سرعت نور است. مربوطه{\displaystyle f_{r,s}}فرکانس برخورد جبهه‌های موج به گیرنده در کادر منبع، برابر است با{\displaystyle f_{r,s}=1/t_{r,s}=f_{s}(1-\بتا).}

تا کنون، معادلات با معادلات اثر داپلر کلاسیک با یک منبع ثابت و یک گیرنده متحرک یکسان بوده است.

با این حال، به دلیل اثرات نسبیتی، ساعت‌های گیرنده نسبت به ساعت‌های منبع گشاد زمان هستند:{\displaystyle t_{r}=t_{r,s}/\gamma }، که{\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}}عامل لورنتس است . برای اینکه بدانیم کدام زمان گشاد شده است، آن را به یاد می آوریم {\displaystyle t_{r,s}}زمانی در قاب است که منبع در آن استراحت می کند. گیرنده فرکانس دریافتی را اندازه گیری می کند

{\displaystyle f_{r}=f_{r,s}\gamma }{\displaystyle ={\frac {1-\beta }{\sqrt {1-\beta ^{2}}}}f_{s}}{\displaystyle ={\sqrt {\frac {1-\beta }{1+\beta }}}\,f_{s}.}