ز ویکیپدیا، دانشنامه آزاد
بخشی از یک سریال در
مکانیک کلاسیک
قانون دوم حرکت
- تاریخ
- جدول زمانی
- کتاب های درسی
نشان می دهد
شاخه ها
نشان می دهد
مبانی
پنهان شدن
فرمولاسیون
قوانین حرکت نیوتن
- مکانیک تحلیلی
- مکانیک لاگرانژی
- مکانیک هامیلتونی
- مکانیک روتین
- معادله همیلتون-ژاکوبی
- معادله حرکت اپل
- مکانیک کوپمن-فون نیومن
نشان می دهد
موضوعات اصلی
نشان می دهد
چرخش
نشان می دهد
دانشمندان
پورتال فیزیک
دسته بندی
- v
- تی
- ه
جوزف-لوئیس لاگرانژ (1736-1813)
در فیزیک ، مکانیک لاگرانژی فرمول بندی مکانیک کلاسیک است که بر اساس اصل کنش ساکن (همچنین به عنوان اصل کمترین عمل شناخته می شود) بنا شده است. این توسط ریاضیدان و ستاره شناس ایتالیایی-فرانسوی جوزف-لوئیس لاگرانژ در اثر خود در سال 1788، مکانیک تحلیلی معرفی شد . [1]
مکانیک لاگرانژی یک سیستم مکانیکی را به صورت یک جفت توصیف می کند
اصل عمل ثابت مستلزم آن است که عملکرد عملکرد سیستم از آن ناشی شود
مقدمه [ ویرایش ]
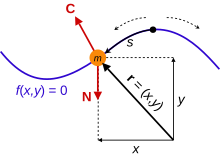
مهره برای حرکت روی سیم بدون اصطکاک محدود شده است. سیم یک نیروی واکنش C بر روی مهره وارد می کند تا آن را روی سیم نگه دارد. نیروی غیر محدودیتی N در این حالت گرانش است. توجه داشته باشید که موقعیت اولیه سیم می تواند منجر به حرکات مختلفی شود.
آونگ ساده. از آنجایی که میله صلب است، موقعیت باب مطابق با معادله f ( x , y ) = 0 محدود می شود، نیروی محدودیت C کشش در میله است. باز هم نیروی غیر محدود N در این مورد گرانش است.
فرض کنید مهرهای وجود دارد که روی یک سیم میچرخد، یا یک آونگ ساده در حال چرخش . اگر هر یک از اجسام عظیم (مهره، باب آونگ) را به عنوان یک ذره ردیابی کنیم، محاسبه حرکت ذره با استفاده از مکانیک نیوتنی نیاز به حل نیروی محدودیت متغیر با زمان لازم برای نگه داشتن ذره در حرکت محدود (نیروی واکنش) دارد. اعمال شده توسط سیم بر روی مهره، یا کشش در میله آونگ). برای همین مسئله با استفاده از مکانیک لاگرانژی، به مسیری که ذره می تواند طی کند نگاه می کند و مجموعه ای مناسب از مختصات تعمیم یافته مستقل را انتخاب می کند. که کاملاً حرکت احتمالی ذره را مشخص می کند. این انتخاب نیاز به نیروی محدودیت برای ورود به سیستم معادلات حاصل را از بین می برد. معادلات کمتری وجود دارد زیرا کسی مستقیماً تأثیر محدودیت بر ذره را در یک لحظه معین محاسبه نمی کند.
برای طیف گسترده ای از سیستم های فیزیکی، اگر اندازه و شکل یک جسم عظیم ناچیز باشد، ساده سازی آن به عنوان یک ذره نقطه ای ساده است . برای سیستمی از ذرات نقطه ای N با جرم m 1 , m 2 , ..., m N , هر ذره دارای یک بردار موقعیت است که به r 1 , r 2 , ..., r N نشان داده می شود . مختصات دکارتی اغلب کافی است، بنابراین r 1 = ( x 1 , y 1 , z 1)، r 2 = ( x 2 , y 2 , z 2 ) و غیره. در فضای سه بعدی ، هر بردار موقعیت به سه مختصات نیاز دارد تا مکان یک نقطه را به طور یکتا تعریف کند، بنابراین 3 N مختصات برای تعریف منحصر به فرد پیکربندی سیستم وجود دارد. همه اینها نقاط خاصی در فضا برای تعیین مکان ذرات هستند. یک نقطه کلی در فضا r = ( x , y , z ) نوشته می شود. سرعت هر ذره سرعت حرکت ذره در مسیر حرکت خود است و مشتق زمانی است .از موقعیت خود، بنابراین
∑اف=مترد2دتی2
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.