هندسه اقلیدسی [ ویرایش ]

یک مثلث در هواپیما

در مورد هواپیمای اقلیدسی ، گروه تقارن گروه حرکات اقلیدسی است ، محصول نیمه کاره گروه ترجمه دو بعدی توسط گروه چرخش است. [44] ژئودزیک خطوط مستقیمی است و هندسه در فرمول های ابتدایی مثلثات مانند قانون کسین برای یک مثلث با دو طرف A ، b ، c و زاویه های α ، β ، γ رمزگذاری می شود :

c ^ {2} = a ^ {2} + b ^ {2} -2ab \، \ cos \ gamma.

Tori Flat را می توان با گرفتن قطعه R 2 توسط یک شبکه ، یعنی زیر گروه Abelian رایگان از درجه 2 بدست آورد. این سطوح بسته هیچ اختلافی ایزومتریک در E 3 ندارند . با این وجود ، آنها جابجایی های ایزومتریک در E 4 را می پذیرند . در ساده ترین حالت این از این واقعیت ناشی می شود که توروس محصولی از دو دایره است و هر دایره می تواند به صورت ایزومتریک در E 2 تعبیه شود . [45]

هندسه کروی [ ویرایش ]

همچنین ببینید: مثلثات کروی و مثلث کروی

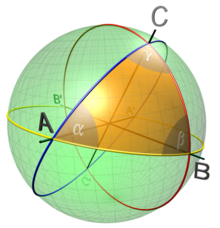
مثلث کروی

مساحت مثلث کروی در کره واحد α + β + γ - π است .

گروه ایزومتری واحد واحد S 2 در E 3 گروه متعامد O (3) است ، با گروه چرخش SO (3) به عنوان زیر گروه ایزومتری ها که جهت گیری را حفظ می کنند. این محصول مستقیم است SO (3) با نقشه واقع در طرف مقابل ، ارسال X به - X . [46] گروه SO (3) بطور گذرا بر روی S 2 عمل می کند . زیر گروه تثبیت کننده بردار یکه (0،0،1) را می توان با شناسایی SO (2) ، به طوری که S 2 = SO (3) / SO (2) .

ژئودزیک بین دو نقطه در کره ، قوس های دایره ای بزرگ با این نقاط انتهایی داده شده است. اگر نقاط ضد پاد نباشند ، کوتاهترین ژئودزیکی منحصر به فرد بین نقاط وجود دارد. این ژئودزیک نیز می تواند به صورت تئوری به صورت گروهی توصیف شود: هر ژئودزیکی از طریق قطب شمال (0/0،1) مدار زیر گروه چرخش های مربوط به یک محور از طریق نقاط ضد پاد در استوا است.

مثلث کروی یک مثلث متشکل از سطوح هندسی در کره است. توسط نقاط A ، B ، C بر روی کره با طرفین BC ، CA ، AB تعریف شده است که از قوسهای دایره بزرگی به طول کمتر از π تشکیل شده است . اگر طول ضلع ها a ، b ، c و زوایای بین طرفین α ، β ، γ باشد ، پس قانون کسین کروی بیان می کند که

\ cos c = \ cos a \، \ cos b + \ sin a \، \ sin b \، \ cos \ gamma.

مساحت مثلث توسط

مساحت = α + β + γ - π .

با استفاده از طرح ریزی استریوگرافی از قطب شمال ، کره را می توان با هواپیمای پیچیده C ∪ {∞ identified مشخص کرد . نقشه صریح توسط داده شده است

\ pi (x ، y ، z) = x + iy \ over 1-z} \ equiv u + iv.

تحت این مکاتبات ، هر چرخش S 2 با یک تغییر Möbius در SU (2) مطابقت دارد ، که منحصر به فرد برای ثبت نام است. [47] با توجه به مختصات ( u ، v ) در صفحه پیچیده ، متریک کروی تبدیل می شود [48]

ds ^ {2} = {4 (du ^ {2} + dv ^ {2}) \ over (1 + u ^ {2} + v ^ {2}) ^ {2}}.

کره واحد سطح منحصر به فرد با جهت گیری بسته منحنی با انحنای ثابت 1+ است. مقدار SO (3) / O (2) را می توان با هواپیمای واقعی پروژکتور شناسایی کرد . این غیر جهت گرا است و می تواند به عنوان قطعه S 2 توسط نقشه ضد پاد (ضرب با − 1) توصیف شود. کره به سادگی به هم متصل است ، در حالی که هواپیمای پروژکتور واقعی دارای گروه اساسی Z 2 است . زیر گروه متناهی از SO (3) ، مربوط به زیر گروه متناهی از O (2) و گروه های تقارن اجسام افلاطونی ، آزادانه در عمل نمی S 2 ، به طوری که خارج قسمت مربوطه 2-منیفولدهای، فقط orbifolds.

هندسه قند خون [ ویرایش ]

همچنین ببینید: مثلث هایپربولیک و هندسه هایپربولی

هنری پینکاره (1912-1994)

هندسه غیر اقلیدسی [49] برای اولین بار در نامه های گاوس مورد بحث قرار گرفت ، که محاسبات گسترده ای را در اواخر قرن نوزدهم انجام داد که اگرچه به صورت خصوصی به گردش در آمد ، وی تصمیم گرفت تا چاپ نکند. در سال 1830 لوباچفسکی و بطور مستقل در سال 1832 بولیوی ، پسر یکی از خبرنگاران گاوس ، نسخه های مصنوعی از این هندسه جدید را منتشر کرد ، که برای آنها مورد انتقاد شدید قرار گرفت. با این حال ، تا سال 1868 نگذشته بود که بلترامی ، به دنبال آن کلین در 1871 و Poincaré در 1882 ، مدلهای تحلیلی بتنی را برای آنچه کلین لقب هندسه هذلولی هذلولی ارائه داد . چهار مدل هندسه هایپربولیک دو بعدی که پدیدار شدند:

مدل اول ، مبتنی بر دیسک ، این مزیت را دارد که ژئودزیک در واقع قطعه خط است (یعنی تقاطع خطوط اقلیدسی با دیسک واحد باز). مدل آخر این مزیت را دارد که ساختاری را ارائه می دهد که کاملاً موازی با حوزه واحد در فضای 3 بعدی اقلیدسی است. به دلیل کاربرد آنها در تجزیه و تحلیل پیچیده و هندسه ، مدلهای Poincaré بیشترین کاربرد را دارند: به لطف تحولات Mbibius بین دیسک و نیم صفحه بالایی قابل تعویض هستند.

اجازه دهید

D = \ {z \، \ col | z | <1 \

شود دیسک پوانکاره در صفحه مختلط با متریک پوانکاره

ds ^ {2} = {4 (dx ^ {2} + dy ^ {2}) \ over (1-x ^ {2} -y ^ {2}) ^ {2}}.

در مختصات قطبی ( r ، θ ) متریک توسط داده می شود

ds ^ {2} = {4 (dr ^ {2} + r ^ {2} \، d \tata ^ {2}) \ over (1-r ^ {2}) ^ {2}.

طول منحنی γ : [ a ، b ] → D توسط فرمول داده می شود

\ ell (\ gamma) = \ int _ {a} ^ {b} {2 | \ gamma ^ {\ Prime (t) | \، dt \ over 1- | \ gamma (t) | ^ {2} .

گروه G = SU (1،1) داده شده توسط

G = \ سمت چپ \ {{\ شروع {pmatrix} \ alpha & \ beta \\ over \ overline {\ beta}} & {\ overline {\ alpha}} \ end {pmatrix}}: \ alpha، \ beta \ in \ mathbf {C} ، \، | \ alpha | ^ {2} - | \ beta | ^ {2} = 1 \ Right \

بطور گذرا با تحولات Möbius روی D عمل می کند و زیر گروه تثبیت کننده 0 گروه چرخش است

K = \ سمت چپ \ {{\ شروع {pmatrix} \ zeta & 0 \\ 0 & {\ overline {\ zeta}} \ end {pmatrix}}: \ zeta \ in \ mathbf {C}، \، | \ zeta | = 1 \ درست \

گروه سود SU (1،1) / ± I گروه ایزومتری های حفظ جهت گیری D است . هر دو نقطه z ، w در D توسط یک ژئودزیک منحصر به فرد ، توسط بخشی از دایره یا خط مستقیم که از Z و W عبور می کند و به صورت دایره مرزی به دایره مرزی داده می شود ، پیوسته است. فاصله بین z و w توسط داده شده است

\ displaystyle d (z، w) = 2 \ tanh ^ {- 1} {\ frac {| zw |} {| 1 - {\ overline {w}} z |}}.

به طور خاص d (0 ، r ) = 2 tanh -1 r و c ( t ) =1/2tanh t از لحاظ ژئودزیکی از طریق 0 در امتداد محور واقعی ، پارامتر شده توسط arcl طول است.

توپولوژی تعریف شده توسط این متریک معادل توپولوژی معمولی اقلیدسی است ، اگرچه به عنوان یک فضای متریک ( D ، D ) کامل است.

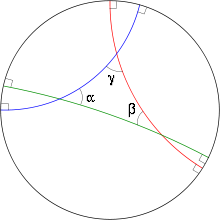
مثلث هذلولی در مدل دیسک Poincaré

مثلث هذلولی یک مثلث متشکل از سطوح هندسی برای این اندازه گیری است: هر سه نقطه در D رئوس یک مثلث هذلولی هستند. اگر ضلع ها دارای طول a ، b ، c با زاویه های مربوطه α ، β ، γ باشند ، بنابراین قاعده کسین کربن بیان می کند که

\ cosh c = \ cosh a \، \ cosh b- \ sinh a \، \ sinh b \، \ cos \ gamma.

مساحت مثلث هایپربولیک توسط [50] داده شده است

مساحت = π - α - β - γ .

دیسک واحد و نیم صفحه فوقانی

H = \ {w = x + iy \، \ colon \، y> 0 \

با تحولات Möbius مطابقتاً معادل دارند

w = i {1 + z \ over 1-z}، \، \، z = i wi \ over w + i.

بر اساس این مکاتبات عمل SL (2، R) توسط تحولات موبیوس در H مربوط به آن از SU (1،1) در D . متریک در H می شود

ds ^ {2} = {dx ^ {2} + dy ^ {2} \ over y ^ {2}.

از آنجا که خطوط یا دایره ها تحت دگرگونی های Möbius حفظ می شوند ، ژئودزیک دوباره توسط خطوط یا دایره هایی به صورت متعامد به محور واقعی توصیف می شود.

دیسک واحد با متریک Poincaré منیفولد ریمانیایی دو بعدی به سادگی متمرکز با منحنی ثابت −1 است. هر سطح بسته بسته M با این خاصیت دارای D است به عنوان فضای پوشش جهانی آن. آن گروه اساسی را می توان با concompact زیر گروه رایگان چرخش شناسایی Γ از SU (1،1) ، در چنین راهی که

م = \ گاما \ برگشت به لبه G / K.

در این حالت Γ یک گروه کاملاً ارائه شده است . ژنراتورها و روابط در یک چند ضلعی ژئودزیک بنیادی محدب محور جغرافیایی در D (یا H ) متناظر هندسی با ژئودزیک بسته در M کدگذاری می شوند .

نمونه .

یکنواختی [ ویرایش ]

همچنین ببینید: قضیه یکسان سازی

با توجه به سطح بسته M جهت دار با انحنای K گاوسی ، متریک روی M می تواند با مقیاس بندی آن توسط یک عامل e 2 u مطابق با هم تغییر کند . سپس انحنای جدید گاوسی K ′ داده می شود

K ^ {\ Prime (x) = e ^ {- 2u} (K (x) - \ Delta u) ،

که در آن Δ لاپلاسیان برای متریک اصلی است. بنابراین نشان می دهد که یک سطح معادل با یک معیار با انحنای ثابت K معادل است. برای حل نوع زیر معادله لیویل کافی است :

\ Delta u = K ^ {\ Prime} e ^ {2u} + K (x).

هنگامی که M دارای مشخصه اویلر 0 است ، به همان نسبت یک گورخا تفاوت دارد ، K ′ 0 ، بنابراین این مقدار در حل است

\ Delta u = K (x).

با تئوری بیضوی استاندارد ، این امکان پذیر است زیرا انتگرال K بر M صفر است با قضیه گاوس-بنت. [51]

وقتی M دارای خصوصیات منفی اویلر باشد ، K ′ = −1 ، بنابراین معادله قابل حل است:

\ Delta u = -e ^ {2u} + K (x).

با استفاده از استمرار نقشه نمایی در فضای سوابولف به دلیل نیل ترودینجر ، این معادله غیر خطی همیشه قابل حل است. [52]

سرانجام در مورد 2 حوزه ، K ′ = 1 و معادله می شود:

\ Delta u = e ^ {2u} + K (x).

تاکنون این معادله غیر خطی به طور مستقیم مورد تجزیه و تحلیل قرار نگرفته است ، اگرچه نتایج کلاسیک مانند نظریه ریمان-روچ دلالت بر این دارد که همیشه راه حل دارد. [53] روش جریان ریچی ، که توسط ریچارد اس. همیلتون ساخته شده است ، اثبات دیگری بر وجود مبتنی بر معادلات دیفرانسیل جزئی غیر خطی برای اثبات وجود دارد. [54] در حقیقت ، جریان Ricci بر روی اندازه های کنفورماسی در S 2 در توابع u ( x ، t ) تعریف شده است.

u_ {t} = 4 \ pi -K '(x، t) = 4 \ pi -e ^ {- 2u} (K (x) - \ Delta u).

پس از زمان محدود ، چو نشان داد که K K مثبت می شود. نتایج قبلی از همیلتون می تواند مورد استفاده قرار گیرد تا نشان دهد K K به 1+ تبدیل می شود. [55] پیش از این نتایج در مورد جریان ریچی ، اسگود ، فیلیپس و سارناک (1988) رویکردی جایگزین و تکنیکی ساده تر برای یکنواختی را بر اساس جریان در معیارهای ریمانی g تعریف شده توسط log det Δ g ارائه داده بودند .

یک اثبات ساده با استفاده از تنها عملگرهای بیضوی کشف شده در 1988 می توان در دینگ یافت (2001) . اجازه دهید G باشد تابع گرین در S 2 رضایت Δ G = 1 + 4π δ P ، که در آن δ P اندازه گیری نقطه در یک نقطه ثابت است P از S 2 . معادله Δ v = 2 K - 2 ، یک راه حل v صاف دارد ، زیرا سمت راست دارای 0 انتساب توسط قضیه گاوس-بنت است. بنابراین φ = 2 G + v برآورده می کندΔ φ = 2 K از P فاصله دارد . از این رو نتیجه می گیرد که g 1 = e φ g یک متریک کامل از انحنای ثابت 0 بر روی مکمل P است ، بنابراین از نظر هواپیما ایزومتریک است. آهنگسازی با طرح stereographic ، آن را زیر است که یک تابع صاف وجود دارد تو که الکترونیکی 2 تو گرم است گاوسی در مکمل انحنای 1 P . عملکرد تو به طور خودکار بر روی یک عملکرد صاف در کل S 2 گسترش می یابد . [ج]

منبع

https://en.wikipedia.org/wiki/Differential_geometry_of_surfaces