خواص [ ویرایش ]

لم تقسیم می گوید که اگر توالی دقیق کوتاه

{\displaystyle 0\to A\;{\xrightarrow {\ f\ }}\;B\;{\xrightarrow {\ g\ }}\;C\to 0}

اذعان ریخت تی  : B → به طوری که تی ∘ F هویت است یا ریخت تو : C → B به طوری که گرم ∘ تو هویت است C ، پس از آن B است مجموع مستقیم از و C (برای غیر گروه های جابه جایی، این یک محصول نیمه مستقیم است ). یکی می گوید که چنین توالی دقیق کوتاهی تقسیم می شود .

مار لم نشان می دهد که چگونه یک نمودار جابجایی با دو ردیف دقیق افزایش می دهد به یک توالی طولانی تر دقیق. نه لم یک مورد خاص است.

پنج لم شرایطی که تحت آن نقشه وسط در یک نمودار جابجایی با ردیف دقیق طول 5 ریخت است می دهد. کوتاه پنج لم یک مورد خاص آن استفاده به توالی دقیق کوتاه است.

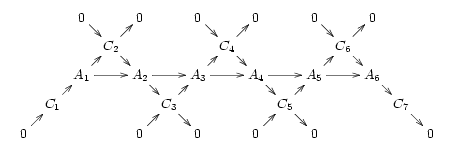
اهمیت توالی‌های دقیق کوتاه با این واقعیت مشخص می‌شود که هر دنباله دقیق از «بافته شدن» چندین سکانس دقیق کوتاه با هم تداخل دارند. به عنوان مثال دنباله دقیق را در نظر بگیرید

A_{1}\به A_{2}\به A_{3}\به A_{4}\به A_{5}\به A_{6}

که به این معنی است که اشیاء C k در این دسته وجود دارد به طوری که

C_{k}\cong \ker(A_{k}\to A_{k+1})\cong \operatorname {im} (A_{k-1}\to A_{k}).

علاوه بر این، فرض کنید هم‌شکلی هر مورفیسم وجود داشته باشد و با تصویر مورفیسم بعدی در دنباله هم‌شکل باشد:

C_{k}\cong \operatorname {coker} (A_{k-2}\to A_{k-1})

(این درست است برای تعدادی از دسته های جالب، از جمله هر دسته آبلی مانند گروه های abelian است؛ اما این درست برای همه مقوله های است که اجازه می دهد توالی دقیق نیست، و به طور خاص است درست است برای نه دسته از گروه ، که در آن کوکر ( ج ): G → H است H / IM ( F ) امH/{\left\langle \operatorname {im} f\right\rangle }^{H}ضریب H با بسته شدن مزدوج im( f ).) سپس یک نمودار جابجایی به دست می آوریم که در آن تمام قطرها دنباله های دقیق کوتاه هستند:

توالی های دقیق کوتاه طولانی.png

تنها بخشی از این نمودار که به شرایط کوکرنل بستگی دارد شی است {\textstyle C_{7}} و جفت نهایی مورفیسم {\textstyle A_{6}\to C_{7}\to 0}. اگر شیئی وجود داردA_{{k+1}} و مورفیسم {\displaystyle A_{k}\to A_{k+1}} به طوری که }{\displaystyle A_{k-1}\to A_{k}\to A_{k+1}} دقیق است، سپس دقت {\displaystyle 0\to C_{k}\to A_{k}\to C_{k+1}\to 0}تضمین شده است. مجدداً مقوله گروه‌ها را مثال می‌زنیم، این واقعیت که im( f ) هسته برخی هم‌مورفیسم‌ها در H است، نشان می‌دهد که آن یک زیرگروه عادی است که با بسته شدن مزدوج آن منطبق است. بنابراین کوکر( f ) با تصویر H /im( f ) شکل بعدی هم شکل است.

برعکس، با توجه به هر فهرستی از توالی‌های دقیق کوتاه که همپوشانی دارند، عبارت‌های میانی آنها یک دنباله دقیق را به همان شیوه تشکیل می‌دهند.

کاربرد توالی های دقیق [ ویرایش ]

در تئوری دسته‌بندی‌های آبلی، توالی‌های دقیق کوتاه اغلب به‌عنوان زبانی مناسب برای صحبت درباره اشیاء فرعی و عاملی استفاده می‌شوند.

مشکل پسوند است که در اصل این پرسش که "با توجه به شرایط پایان و C از یک توالی دقیق کوتاه، چه احتمالات را برای حد وسط وجود داشته باشد ب ؟" در دسته گروه ها، این معادل این سوال است که کدام گروه B دارای A به عنوان زیرگروه نرمال و C به عنوان گروه عامل مربوطه هستند؟ این مشکل در طبقه بندی گروه ها حائز اهمیت است . گروه اتومورفیسم بیرونی را نیز ببینید .

توجه داشته باشید که در دنباله دقیق، ترکیب F من 1 ∘ F من نقشه من به 0 در من 2 ، بنابراین هر توالی دقیق است زنجیره ای پیچیده . علاوه بر این، فقط f i -تصاویر عناصر A i با f i +1 به 0 نگاشت می‌شوند ، بنابراین همسانی این مجموعه زنجیره بی‌اهمیت است. به طور خلاصه تر:

توالی های دقیق دقیقاً مجموعه های زنجیره ای هستند که غیر حلقوی هستند .

بنابراین، با توجه به هر مجموعه زنجیره ای، همسانی آن را می توان به عنوان معیاری برای میزان دقیق بودن آن در نظر گرفت.

اگر مجموعه‌ای از دنباله‌های دقیق کوتاه را که توسط کمپلکس‌های زنجیره‌ای به هم مرتبط شده‌اند در نظر بگیریم (یعنی دنباله‌ای دقیق کوتاه از مجتمع‌های زنجیره‌ای، یا از دیدگاهی دیگر، مجموعه‌ای زنجیره‌ای از توالی‌های دقیق کوتاه)، آن‌گاه می‌توانیم از این یک نتیجه دقیق طولانی استخراج کنیم. دنباله (یعنی یک دنباله دقیق نمایه شده توسط اعداد طبیعی) در همسانی با استفاده از لم زیگزاگ . آن را در توپولوژی جبری در مطالعه همسانی نسبی می آید . توالی مایر Vietoris مثال دیگری است. توالی های دقیق طولانی القا شده توسط توالی های دقیق کوتاه نیز مشخصه تابع های مشتق شده هستند .

functors دقیق هستند functors که تبدیل توالی دقیق را به توالی دقیق.

منبع

https://en.wikipedia.org/wiki/Exact_sequence