معادله دیراک

توسط علی رضا نقش نیلچی | جمعه بیست و ششم خرداد ۱۴۰۲ | 14:11

معادله دیراک

برای ادامه به سمت یک نظریه میدان برای الکترون ها و کوانتیزه کردن میدان دیراک، ما می خواهیم یک لاگرانژی اسکالر پیدا کنیم که معادله دیراک را به دست می دهد. از مطالعه کوواریانس‌های لورنتس می‌دانیم که یک اسکالر است و می‌توانیم از حاصلضرب نقطه‌ای دو بردار 4 مانند لاگرانژی زیر یک اسکالر تشکیل دهیم. لاگرانژی نمی تواند به طور صریح به مختصات وابسته باشد. 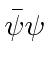$\bgroup\color{black}$\bar{\psi}\psi$\egroup$

$\begin{displaymath}\bgroup\color{black} {\cal L}=-c\hbar\bar{\psi}\gamma_\mu{\partial\over\partial x_\mu}\psi-mc^2\ نوار{\psi}\psi \egroup\end{displaymath}$

(می‌توانیم یک جمله تانسور هم اضافه کنیم اما برای بدست آوردن معادله دیراک نیازی نیست.) فیلدهای مستقل 4 جزء $\bgroup\color{black}$\psi$\egroup$ و چهار جزء $\bgroup\color{black}$\bar{\psi}$\egroup$ . معادله اویلر -لاگرانژ با استفاده از میدان‌های مستقل ساده است زیرا هیچ مشتقی از آن در لاگرانژ $\bgroup\color{black}$\bar{\psi}$\egroup$ وجود ندارد . $\bgroup\color{black}$\bar{\psi}$\egroup$

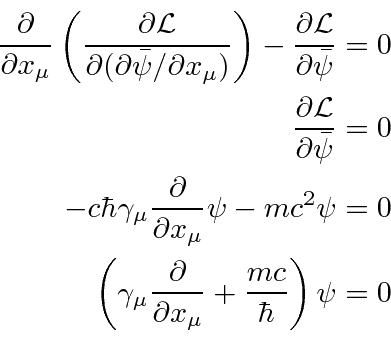
$\begin{eqnarray*} {\partial\over\partial x_\mu}\left({\partial{\cal L}\over\part... ...\mu{\partial\over\partial x_\mu }+{mc\over\hbar}\right)\psi=0 \\ \end{eqnarray*}$

این معادله دیراک را به ما می دهد که نشان می دهد این لاگرانژی درست است. معادله اویلر-لاگرانژ که با استفاده از فیلدها به دست می آید ، معادله الحاقی دیراک $\bgroup\color{black}$\psi$\egroup$ است .

چگالی همیلتونی ممکن است از لاگرانژ به روش استاندارد گرفته شود و کل همیلتون با ادغام در فضا محاسبه شود. توجه داشته باشید که چگالی همیلتونی همان چگالی همیلتونی است که مستقیماً از معادله دیراک مشتق شده است.

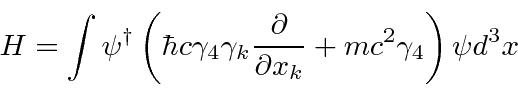
$\begin{displaymath}\bgroup\color{black} H=\int\psi^\dagger\left(\hbar c\gamma_4\... ...\partial\over\partial x_k}+mc^2\gamma_4 \right)\psi d^3x \egroup\end{displaymath}$

ما ممکن است $\bgroup\color{black}$\psi$\egroup$ در امواج صفحه گسترش پیدا کنیم تا همیلتونی را به عنوان مجموع نوسانگرها درک کنیم.

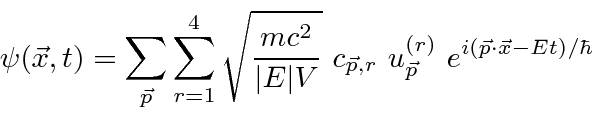
$\begin{displaymath}\bgroup\color{black} \psi(\vec{x},t)=\sum\limits_{\vec{p}}\su... ... u^{(r)} _{\vec{p}} e^{i(\vec{p}\cdot\vec{x}-Et)/\hbar} \egroup\end{displaymath}$

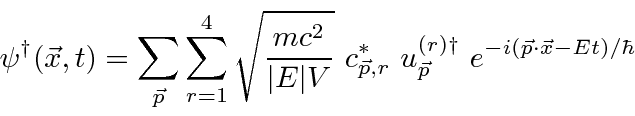
$\begin{displaymath}\bgroup\color{black} \psi^\dagger(\vec{x},t)=\sum\limits_{\ve... ...خنجر}_{\vec{p}} e^{-i(\vec{p}\cdot\vec{x}-Et)/\hbar} \egroup\end{displaymath}$

با نوشتن همیلتونی بر حسب این فیلدها ، فرمول را می توان با بازدهی ساده کرد

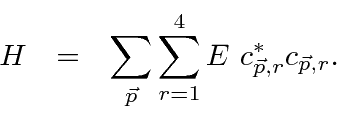
$\begin{eqnarray*} H&=&\sum\limits_{\vec{p}}\sum\limits_{r=1}^4 E c_{\vec{p},r}^*c_{\vec{p },r}. \\ \پایان{eqnarray*}$

با قیاس با الکترومغناطیس، می‌توانیم ضرایب فوریه را برای امواج صفحه دیراک توسط عملگرها جایگزین کنیم.

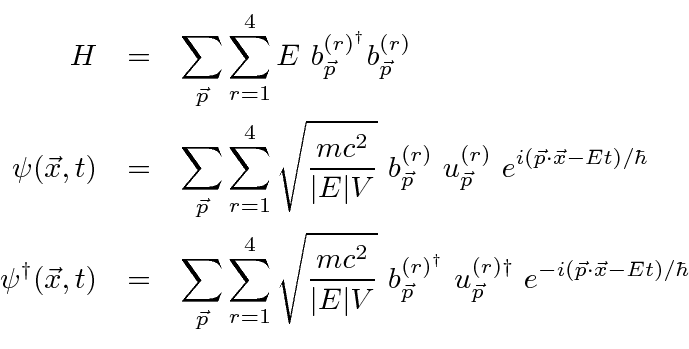
$\begin{eqnarray*} H&=&\sum\limits_{\vec{p}}\sum\limits_{r=1}^4 E b^{(r)^\dagger... ...{(r )\dagger}_{\vec{p}} e^{-i(\vec{p}\cdot\vec{x}-Et)/\hbar} \\ \end{eqnarray*}$

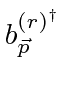
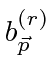
ایجاد عملگرهای نابودی و برآوردن روابط ضد کموتاسیون . $\bgroup\color{black}$b^{(r)^\dagger}_{\vec{p}}$\egroup$ $\bgroup\color{black}$b^{(r)}_{\vec{p}}$\egroup$

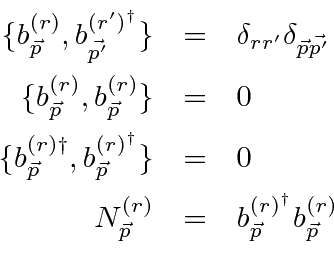
$\{begin{eqnarray*} \{b^{(r)}_{\vec{p}},b^{(r')^\dagger}_{\vec{p'}}\}&=&\ delta_{rr... ...{(r)}_{\vec{p}}&=&b^{(r)^\dagger}_{\vec{p}}b^{(r)}_ {\vec{p}} \\ \end{eqnarray*}$

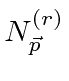$\bgroup\color{black}$N^{(r)}_{\vec{p}}$\egroup$ اپراتور شماره شغل است. روابط ضد جابجایی تعداد اشغال را 1 یا 0 محدود می کند .

اکنون میدان دیراک و همیلتونین را می‌توان بر حسب میدان‌های الکترونی و پوزیترونی بازنویسی کرد که انرژی برای آنها همیشه مثبت است، با جایگزین کردن عملگر برای از بین بردن یک "حالت انرژی منفی" با یک عملگر برای ایجاد یک حالت پوزیترون با تکانه مناسب و چرخش.

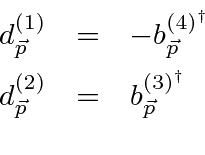
$\begin{eqnarray*} d^{(1)}_{\vec{p}}&=&-b^{(4)^\dagger}_{\vec{p}} \\ d^{(2 )}_{\vec{p}}&=&b^{(3)^\dagger}_{\vec{p}} \\ \end{eqnarray*}$

این ضد رفت و آمد با هر چیز دیگری به استثنای اینکه

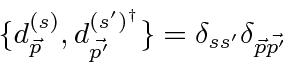
$\begin{displaymath}\bgroup\color{black} \{d^{(s)}_{\vec{p}},d^{(s')^\dagger}_{\vec{p'}} \}=\delta_{ss'}\delta_{\vec{p}\vec{p'}} \egroup\end{displaymath}$

حالا فیلدها و همیلتونین را بازنویسی کنید.

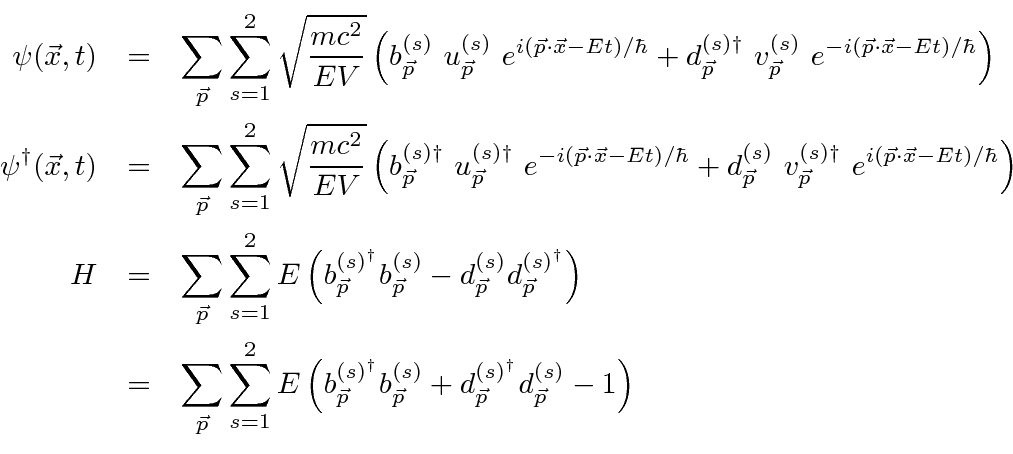
$\begin{eqnarray*} \psi(\vec{x},t)&=&\sum\limits_{\vec{p}}\sum\limits_{s=1}^2\sqr... ... vec{p}} +d^{(s)^\dagger}_{\vec{p}}d^{(s)}_{\vec{p}}-1\right) \\ \end{eqnarray *}$

تمام انرژی های این حالت ها مثبت است .

یک انرژی ثابت (بی نهایت) مشابه اما دارای علامت مخالف با میدان EM کوانتیزه شده وجود دارد که باید آن را اضافه کنیم تا حالت خلاء انرژی صفر داشته باشد. توجه داشته باشید که اگر از اپراتورهای رفت و آمد (بوز-اینشتین) به جای ضد رفت و آمد استفاده می کردیم، کمترین حالت پایه انرژی وجود نداشت، بنابراین این تفریق انرژی ممکن نبود. آمار فرمی دیراک برای ذراتی که معادله دیراک را برآورده می کنند مورد نیاز است .

از آنجایی که عملگرهایی که حالت‌های فرمیونی را ایجاد می‌کنند ضد جابه‌جایی هستند ، حالت‌های فرمیونی باید تحت مبادله ضد متقارن باشند. فرض کنید $\bgroup\color{black}$b_r^\dagger$\egroup$ و $\bgroup\color{black}$b_r$\egroup$ عملگرهای ایجاد و نابودی فرمیون ها هستند و آنها ضد رفت و آمد هستند.

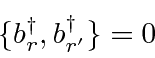
$\begin{displaymath}\bgroup\color{black} \{b_r^\dagger,b_{r'}^\dagger\}=0 \egroup\end{displaymath}$

سپس این حالت ها تحت تبادل جفت فرمیون ها ضد متقارن هستند.

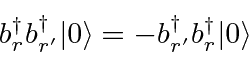
$\begin{displaymath}\bgroup\color{black} b_r^\dagger b_{r'}^\dagger \vert\rangle = -b_{r'}^\dagger b_{r}^\dagger \vert\rangle \ egroup\end{displaymath}$

نشان دادن اینکه عدد اشغال حالت های فرمیونی صفر است یا یک کار سختی نیست .

توجه داشته باشید که اسپینورها معادلات کمی متفاوت زیر را برآورده می کنند .

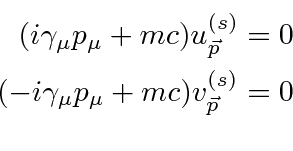
$\begin{eqnarray*} (i\gamma_\mu p_\mu+mc)u^{(s)}_{\vec{p}}=0 \\ (-i\gamma_\mu p_\mu+mc) v^{(s)}_{\vec{p}}=0 \\ \end{eqnarray*}$

منبع

https://quantummechanics.ucsd.edu/ph130a/130_notes/node46.html

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی