​

در فیزیک اتمی ، یک عدد کوانتومی مغناطیسی یک عدد کوانتومی است که برای تشخیص حالت‌های کوانتومی یک الکترون یا ذره دیگر با توجه به تکانه زاویه‌ای آن در امتداد یک محور معین در فضا استفاده می‌شود. عدد کوانتومی مغناطیسی مداری ( ml یا m [ a ] ) اوربیتال‌های موجود در یک زیر پوسته معین از یک اتم را متمایز می‌کند. این مولفه تکانه زاویه‌ای مداری را مشخص می‌کند که در امتداد یک محور معین قرار دارد، که معمولاً محور نامیده می‌شود ، بنابراین جهت مدار را در فضا توصیف می‌کند. عدد کوانتومی مغناطیسی اسپین m s مولفه محور تکانه زاویه ای اسپین را برای ذره ای با عدد کوانتومی اسپین s مشخص می کند . برای یک الکترون، s 1 ⁄ 2 است و m s یا + 1 ⁄ 2 یا − 1⁄ 2 است که اغلب «spi-up» و «spi-dow» یا α و β نامیده می شود. [ 1 ] [ 2 ] اصطلاح مغناطیسی در نام به گشتاور دوقطبی مغناطیسی مرتبط با هر نوع تکانه زاویه ای اشاره دارد، بنابراین حالت هایی که اعداد کوانتومی مغناطیسی متفاوتی دارند، انرژی را در یک میدان مغناطیسی مطابق با اثر زیمن تغییر می دهند . [ 2 ]

چهار عدد کوانتومی که معمولاً برای توصیف حالت کوانتومی یک الکترون در یک اتم استفاده می‌شود، عدد کوانتومی اصلی ، عدد کوانتومی آزیموتال (اوربیتال) است. {\displaystyle \ell }و اعداد کوانتومی مغناطیسی m l و m s . الکترون‌ها در یک لایه فرعی از یک اتم (مانند s، p، d یا f) با مقادیری از{\displaystyle \ell }(0، 1، 2، یا 3). عدد کوانتومی مغناطیسی مداری مقادیر صحیح را در محدوده از{\displaystyle -\ell }به{\displaystyle +\ell }از جمله صفر. [ 3 ] بنابراین زیر پوسته های s، p، d و f هر کدام شامل 1، 3، 5 و 7 اوربیتال هستند. هر یک از این اوربیتال ها می توانند حداکثر دو الکترون (با اسپین های مخالف) را در خود جای دهند که اساس جدول تناوبی را تشکیل می دهند .

سایر اعداد کوانتومی مغناطیسی نیز به طور مشابه تعریف می‌شوند، مانند mj برای جزء محور ، تکانه زاویه‌ای الکترونیکی j ، [ 1 ] و mI برای اسپین هسته‌ای I. [ 2 ] اعداد کوانتومی مغناطیسی برای نشان دادن مجموع یک سیستم از ذرات، مانند ML یا mL برای کل تکانه زاویه‌ای مداری محور همه الکترون‌های یک اتم، با حروف بزرگ نوشته می‌شوند. [ 2 ]

اشتقاق

[ ویرایش ]

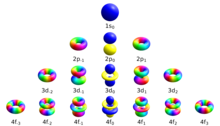
این اوربیتال ها دارای اعداد کوانتومی مغناطیسی هستند{\displaystyle m_{l}=-\ell ,\ldots ,\ell }از چپ به راست به ترتیب صعودی این{\displaystyle e^{m_{l}i\phi }}وابستگی مولفه آزیموتال را می توان به عنوان یک گرادیان رنگ تکراری مشاهده کرد{\displaystyle m_{l}}بار حول محور عمودی

مجموعه ای از اعداد کوانتومی مرتبط با حالت های انرژی اتم وجود دارد. چهار عدد کوانتومی{\displaystyle n}،{\displaystyle \ell }،{\displaystyle m_{l}}، و{\displaystyle m_{s}}حالت کوانتومی کامل یک الکترون را در یک اتم مشخص کنید که تابع موج یا مدار آن نامیده می شود. معادله شرودینگر برای تابع موج یک اتم با یک الکترون یک معادله دیفرانسیل جزئی قابل تفکیک است . (این مورد برای اتم هلیوم خنثی یا اتم های دیگر با الکترون های متقابل متقابل نیست ، که به روش های پیچیده تری برای حل نیاز دارند [ 4 ] ). شعاع، زاویه همپوشانی (یا قطبی) و آزیموت: [ 5 ]

{\displaystyle \psi (r,\theta,\phi )=R(r)P(\theta )F(\phi )}

معادله دیفرانسیل برای{\displaystyle F}در قالب قابل حل است {\displaystyle F(\phi )=Ae^{\lambda \phi }}. زیرا مقادیر زاویه آزیموت{\displaystyle \phi }با 2 تفاوت دارد{\displaystyle \pi } رادیان (360 درجه) نشان دهنده همان موقعیت در فضا و قدر کلی استاف{\displaystyle F}با بزرگی خودسرانه رشد نمی کند{\displaystyle \phi }همانطور که برای یک توان حقیقی، ضریب{\displaystyle \lambda }باید به مضرب عدد صحیح کوانتیزه شود{\displaystyle i}، تولید یک توان مختلط :{\displaystyle \lambda =im_{l}}. [ 6 ] این اعداد صحیح اعداد کوانتومی مغناطیسی هستند. همان ثابت در معادله colatitude ظاهر می شود، جایی که مقادیر بزرگتر از{\displaystyle {m_{l}}^{2}}تمایل به کاهش قدر،{\displaystyle P(\theta)،}و ارزش های{\displaystyle m_{l}}بزرگتر از عدد کوانتومی ازیموتال{\displaystyle \ell }اجازه هیچ راه حلی برای.{\displaystyle P(\theta ).}

رابطه بین اعداد کوانتومی

مداریارزش هاتعداد مقادیر برای{\displaystyle m_{l}}[ 7 ]الکترون در هر زیر پوسته

{\displaystyle \ell =0,\quad m_{l}=0}

{\displaystyle \ell =1,\quad m_{l}=-1,0,+1}

{\displaystyle \ell =2,\quad m_{l}=-2,-1,0,+1,+2}

{\displaystyle \ell =3,\quad m_{l}=-3,-2,-1,0,+1,+2,+3}

{\displaystyle \ell =4,\quad m_{l}=-4,-3,-2,-1,0,+1,+2,+3,+4}

به عنوان جزئی از تکانه زاویه ای

[ ویرایش ]

تصویر تکانه زاویه ای مداری مکانیکی کوانتومی. مخروط ها و صفحه جهت گیری های احتمالی بردار تکانه زاویه ای را نشان می دهند{\displaystyle \ell =2}و{\displaystyle m_{l}=-2,-1,0,1,2}. حتی برای ارزش های افراطی{\displaystyle m_{l}}،{\displaystyle z}- مولفه این بردار کمتر از قدر کل آن است.

محور مورد استفاده برای مختصات قطبی در این تحلیل به صورت دلخواه انتخاب می شود. عدد کوانتومی{\displaystyle m_{l}}اشاره به طرح تکانه زاویه ای در این جهت دلخواه انتخاب شده، که به طور معمول به نام{\displaystyle z}- جهت یا محور کوانتیزاسیون{\displaystyle L_{z}}، بزرگی تکانه زاویه ای در{\displaystyle z}جهت، با فرمول داده می شود: [ 7 ]

{\displaystyle L_{z}=m_{l}\hbar }.

این جزئی از تکانه زاویه ای مداری کل الکترون اتمی است{\displaystyle \mathbf {L} }، که قدر آن به عدد کوانتومی آزیموتال زیر پوسته آن مربوط می شودتوسط معادله:

{\displaystyle L=\hbar {\sqrt {\ell (\ell +1)}}}،

که{\displaystyle \hbar }ثابت پلانک کاهش یافته است . توجه داشته باشید که این{\displaystyle L=0}بر{\displaystyle \ell =0}و تقریبی است{\displaystyle L=\left(\ell +{\tfrac {1}{2}}\right)\hbar }برای بالا{\displaystyle \ell }. اندازه گیری تکانه زاویه ای الکترون در هر سه محور به طور همزمان امکان پذیر نیست. این ویژگی ها اولین بار در آزمایش استرن-گرلاخ توسط اتو استرن و والتر گرلاخ نشان داده شد . [ 8 ]

تاثیر در میدان های مغناطیسی

[ ویرایش ]

عدد کوانتومی{\displaystyle m_{l}}به طور ضعیف به جهت بردار تکانه زاویه ای اشاره دارد . عدد کوانتومی مغناطیسی{\displaystyle m_{l}}تنها در صورتی بر انرژی الکترون تأثیر می گذارد که در یک میدان مغناطیسی باشد زیرا در غیاب آن، همه هارمونیک های کروی مربوط به مقادیر دلخواه مختلف{\displaystyle m_{l}}معادل هستند. عدد کوانتومی مغناطیسی تغییر انرژی یک اوربیتال اتمی را به دلیل میدان مغناطیسی خارجی ( اثر زیمن ) تعیین می‌کند - از این رو به آن عدد کوانتومی مغناطیسی می‌گویند . با این حال، گشتاور دوقطبی مغناطیسی حقیقی یک الکترون در یک اوربیتال اتمی نه تنها از تکانه زاویه‌ای الکترون، بلکه از اسپین الکترون نیز ناشی می‌شود که در عدد کوانتومی اسپین بیان می‌شود.

از آنجایی که هر الکترون دارای یک گشتاور مغناطیسی در یک میدان مغناطیسی است، در معرض گشتاوری خواهد بود که تمایل به ایجاد بردار دارد.L{\displaystyle \mathbf {L} }به موازات میدان، پدیده ای به نام پیشروی لارمور شناخته می شود .

همچنین ببینید

[ ویرایش ]

  • عدد کوانتومی
    • عدد کوانتومی آزیموتالی
    • عدد کوانتومی اصلی
    • عدد کوانتومی را بچرخانید
    • عدد کوانتومی تکانه زاویه ای کل
  • پوسته الکترونی
  • مکانیک کوانتومی پایه
  • اتم بور
  • معادله شرودینگر

    https://en.wikipedia.org/wiki/Magnetic_quantum_number#Effect_in_magnetic_fields

​