مکانیک آماری
نشان می دهد

آمار ذرات

نشان می دهد

مجموعه های ترمودینامیکی

نشان می دهد

مدل ها

نشان می دهد

پتانسیل ها

نشان می دهد

دانشمندان

در فیزیک ، anon نوعی شبه ذره است که تاکنون فقط در سیستم‌های دو بعدی مشاهده شده است . در سیستم های سه بعدی ، تنها دو نوع ذرات بنیادی دیده می شود: فرمیون ها و بوزون ها . Anyon ها دارای ویژگی های آماری واسط بین فرمیون ها و بوزون ها هستند. [ 1 ] به طور کلی، عملیات مبادله دو ذره یکسان ، اگرچه ممکن است باعث تغییر فاز جهانی شود، نمی تواند بر روی قابل مشاهده ها تأثیر بگذارد . Anyon ها به طور کلی به عنوان abelian یا non abelian طبقه بندی می شوند . آنیون های آبلی، که توسط دو آزمایش در سال 2020 شناسایی شدند، [ 2 ] نقش مهمی در اثر هال کوانتومی کسری دارند .

مقدمه

[ ویرایش ]

مکانیک آماری سیستم های بزرگ چند بدنه از قوانینی پیروی می کند که توسط آمار ماکسول-بولتزمن توضیح داده شده است . آمار کوانتومی به دلیل رفتارهای متفاوت دو نوع ذره مختلف به نام فرمیون ها و بوزون ها پیچیده تر است . اما در سیستم های دو بعدی، نوع سومی از ذرات وجود دارد که آنیون نامیده می شود.

در دنیای سه بعدی که ما در آن زندگی می کنیم، تنها دو نوع ذره وجود دارد: "فرمیون ها" که یکدیگر را دفع می کنند و "بوزون ها" که دوست دارند به هم بچسبند. فرمیون رایج، الکترون است که الکتریسیته را حمل می کند. و یک بوزون رایج، فوتون است که نور را حمل می کند. اما در دنیای دو بعدی، نوع دیگری از ذره به نام آنیون وجود دارد که مانند فرمیون یا بوزون رفتار نمی کند.

-  "در نهایت، هر کسی ویژگی های کوانتومی عجیب و غریب خود را آشکار می کند"، بیانیه مطبوعاتی دانشگاه آلتو، آوریل 2020 [ 3 ]

در دنیای دوبعدی، دو آنیون یکسان با جابه‌جایی مکان‌ها به روش‌هایی که در فیزیک سه‌بعدی اتفاق نمی‌افتد، تابع موج خود را تغییر می‌دهند:

در دو بعد، تبادل ذرات یکسان دو بار معادل رها کردن آنها نیست. عملکرد موج ذرات پس از دو بار تعویض مکان ممکن است با حالت اولیه متفاوت باشد. ذرات با چنین آمار مبادله غیرعادی به عنوان آنیون شناخته می شوند. در مقابل، در سه بعد، تبادل ذرات دو بار نمی تواند تابع موج آنها را تغییر دهد، و تنها دو احتمال را برای ما باقی می گذارد: بوزون ها، که تابع موج آنها حتی پس از یک تبادل واحد ثابت می ماند، و فرمیون ها، که مبادله آنها فقط علامت تابع موج آنها را تغییر می دهد.

-  کریل شتنگل، "خانه ای برای هر کسی؟"، فیزیک طبیعت [ 4 ]

این فرآیند مبادله ذرات یکسان، یا چرخش یک ذره به دور ذره دیگر، به عنوان " بافندگی " نامیده می شود. قیطان دو نفره یک رکورد تاریخی از رویداد ایجاد می کند، زیرا عملکردهای موج تغییر یافته آنها تعداد بافته ها را ثبت می کند. [ 5 ]

مایکروسافت در تحقیقات مربوط به هر کسی به عنوان مبنایی بالقوه برای محاسبات کوانتومی توپولوژیکی سرمایه گذاری کرده است . [ 6 ] آنها ممکن است در محاسبات کوانتومی به عنوان شکلی از حافظه مفید باشند. [ 6 ] هرکسی که دور همدیگر بچرخد ("بافندگی") اطلاعات را به روشی قوی تر از سایر فناوری های محاسباتی کوانتومی بالقوه رمزگذاری می کند . [ 7 ] با این حال، بیشتر سرمایه‌گذاری در محاسبات کوانتومی بر اساس روش‌هایی است که از هیچ‌کس استفاده نمی‌کنند. [ 7 ]

تاریخچه

[ ویرایش ]

مانند بسیاری از ایده های عمیق در فیزیک، زیربنای توپولوژیکی هر فرد را می توان به دیراک ردیابی کرد .

-  Biedenharn و همکاران، The Ancestry of the Anyon [ 8 ]

در سال 1977، دو فیزیکدان نظری که در دانشگاه اسلو کار می‌کردند ، Jon Magne Leinaas و Jan Myrheim ، نشان دادند که طبقه‌بندی سنتی ذرات به‌عنوان فرمیون یا بوزون، اگر محدود به حرکت در دو بعد باشند، اعمال نمی‌شود . [ 9 ] ذرات فرضی که نه بوزون هستند و نه فرمیون، انتظار می رود طیف متنوعی از خواص غیرمنتظره قبلی را از خود نشان دهند. در سال 1982، فرانک ویلچک دو مقاله منتشر کرد که در آن آمار کسری شبه ذرات را در دو بعد بررسی می کرد و نام "anyons" را به آنها داد تا نشان دهد که تغییر فاز پس از جایگشت می تواند هر مقداری داشته باشد. [ 10 ]

دانیل تسوئی و هورست استورمر در سال 1982 اثر هال کوانتومی کسری را کشف کردند . [ 11 ] فرانک ویلچک، دن آرواس و رابرت شریفر این بیانیه را در سال 1985 با یک محاسبات صریح که پیش‌بینی می‌کرد ذرات موجود در این سیستم‌ها در واقع همه هستند، تأیید کردند. [ 12 ] [ 13 ]

آنیون آبلیان

[ ویرایش ]

در مکانیک کوانتومی و برخی از سیستم‌های تصادفی کلاسیک، ذرات غیرقابل تمایز این ویژگی را دارند که حالات ذره i را با ذره j مبادله کنند (به طور نمادین {\displaystyle \psi _{i}\leftrightarrow \psi _{j}{\text{ for }}i\neq j}) منجر به حالت چند بدنی متفاوتی نمی شود.

به عنوان مثال، در یک سیستم مکانیک کوانتومی، سیستمی با دو ذره غیر قابل تشخیص، با ذره 1 در حالت ⁠{\displaystyle \psi _{1}}و ذره 2 در حالت{\displaystyle \psi _{2}}، حالت دارد{\displaystyle \left|\psi _{1}\psi _{2}\right\rangle }به علامت دیراک . حال فرض کنید حالات دو ذره را با هم رد و بدل کنیم، آنگاه وضعیت سیستم به این صورت خواهد بود .{\displaystyle \left|\psi _{2}\psi _{1}\right\rangle }. ​این دو حالت نباید یک تفاوت قابل اندازه گیری داشته باشند، بنابراین باید بردار یکسان باشند، تا ضریب فاز :

{\displaystyle \left|\psi _{1}\psi _{2}\right\rangle =e^{i\theta }\left|\psi _{2}\psi _{1}\right\rangle . }

اینجا ،θ{\displaystyle e^{i\theta }}فاکتور فاز است. در فضای سه بعدی یا بیشتر ضریب فاز ⁠ است1{\displaystyle 1}یا​​-1{\displaystyle -1}. ​بنابراین، ذرات بنیادی یا فرمیون هستند که فاکتور فاز آنها ⁠ است-1{\displaystyle -1}یا بوزون هایی که ضریب فاز آنها ⁠ است1{\displaystyle 1}. ​این دو نوع رفتار آماری متفاوتی دارند . فرمیون ها از آمار فرمی دیراک پیروی می کنند ، در حالی که بوزون ها از آمار بوز-انیشتین پیروی می کنند . به طور خاص، فاکتور فاز این است که چرا فرمیون ها از اصل طرد پائولی پیروی می کنند : اگر دو فرمیون در یک حالت باشند، آنگاه داریم

{\displaystyle \left|\psi \psi \right\rangle =-\left|\psi \psi \right\rangle .}

بردار حالت باید صفر باشد، به این معنی که قابل نرمال سازی نیست، بنابراین غیر فیزیکی است.

با این حال، در سیستم‌های دو بعدی، شبه ذرات را می‌توان مشاهده کرد که به طور مداوم از آمارهای فرمی دیراک و بوز-انیشتین تبعیت می‌کنند، همانطور که برای اولین بار توسط Jon Magne Leinaas و Jan Myrheim از دانشگاه اسلو در سال 1977 نشان داده شد. [ 14 ] در مورد دو ذره را می توان به صورت بیان کرد

{\displaystyle \left|\psi _{1}\psi _{2}\right\rangle =e^{i\theta }\left|\psi _{2}\psi _{1}\right\rangle , }

که{\displaystyle e^{i\theta }}می تواند مقادیر دیگری غیر از فقط باشد{\displaystyle -1}یا​​{\displaystyle 1}. ​توجه به این نکته ضروری است که در این عبارت کوتاه، سوء استفاده جزئی از علامت گذاری وجود دارد ، زیرا در واقع این تابع موج می تواند چند ارزشی باشد و معمولاً چند مقدار است. این عبارت در واقع به این معنی است که وقتی ذره 1 و ذره 2 در فرآیندی مبادله می شوند که در آن هر یک از آنها یک نیمه چرخش خلاف جهت عقربه های ساعت در مورد دیگری انجام می دهد، سیستم دو ذره به تابع موج کوانتومی اولیه خود باز می گردد مگر اینکه در واحد هنجار پیچیده ضرب شود. فاکتور فاز e iθ . برعکس، نیم چرخش در جهت عقربه های ساعت باعث ضرب تابع موج در e - iθ می شود . چنین نظریه ای بدیهی است که فقط در دو بعدی معنا پیدا می کند، جایی که جهت عقربه های ساعت و خلاف جهت عقربه های ساعت به وضوح مشخص شده اند.

در مورد θ = π ، آمار فرمی- دیراک ( e iπ = -1 ) و در مورد θ = 0 (یا θ = 2 π ) آمار بوز-اینشتین ( e 2 πi = 1 ) را بازیابی می‌کنیم. در این بین ما چیز متفاوتی داریم. فرانک ویلچک در سال 1982 رفتار چنین شبه ذرات را مورد بررسی قرار داد و اصطلاح "هر" را برای توصیف آنها ابداع کرد، زیرا آنها می توانند هر فازی را در هنگام تعویض ذرات داشته باشند. [ 15 ] بر خلاف بوزون ها و فرمیون ها، هریون ها دارای خاصیت عجیبی هستند که وقتی دو بار به طور یکسان تعویض می شوند (مثلاً اگر هر کدام 1 و هر 2 در خلاف جهت عقربه های ساعت با نیم دور به دور یکدیگر می چرخیدند تا مکان خود را تغییر دهند و سپس در خلاف جهت عقربه های ساعت می چرخیدند. با نیم چرخش در اطراف یکدیگر دوباره به مکان های اصلی خود بازگردند)، تابع موج لزوماً یکسان نیست، بلکه به طور کلی در مقداری پیچیده ضرب می شود. فاز ( در این مثال توسط e 2 iθ ).

همچنین ممکن است از θ = 2 πs با عدد کوانتومی اسپین ذره s استفاده کنیم ، که s برای بوزون‌ها عدد صحیح و برای فرمیون‌ها عدد نیم صحیح است ، به طوری که

{\displaystyle e^{i\theta }=e^{2i\pi s}=(-1)^{2s}،}

یا

{\displaystyle |\psi _{1}\psi _{2}\rangle =(-1)^{2s}|\psi _{2}\psi _{1}\rangle .}

در یک لبه، هر یونهای اثر هال کوانتومی کسری محدود به حرکت در یک بعد فضایی هستند. مدل های ریاضی آنیون های یک بعدی پایه ای از روابط کموتاسیون نشان داده شده در بالا را ارائه می دهند.

در یک فضای موقعیت سه بعدی، عملگرهای آماری فرمیون و بوزون (به ترتیب -1 و 1) فقط نمایش های 1 بعدی از گروه جایگشت (S N ذرات غیر قابل تشخیص N ) هستند که روی فضای توابع موج عمل می کنند. به همین ترتیب، در فضای موقعیت دوبعدی، عملگرهای آماری هریونیک آبلی ( e iθ) فقط نمایش‌های 1 بعدی از گروه قیطان (BN از N ذرات غیر قابل تشخیص) هستند که روی فضای توابع موج عمل می‌کنند. آمارهای هریونیک غیرآبلین، نمایش‌های بعدی بالاتر از گروه قیطان هستند. آمارهای آنیونیک را نباید با آمارهای فراآماری اشتباه گرفت ، که آمار ذرات را توصیف می‌کند که توابع موج آن‌ها نمایش‌هایی با ابعاد بالاتر از گروه جایگشت هستند. [ 16 ] : 22 

هم ارزی توپولوژیکی

[ ویرایش ]

این واقعیت که کلاس‌های هموتوپی مسیرها (یعنی مفهوم هم ارزی روی قیطان‌ها ) اشاره‌ای به بینش ظریف‌تری دارد. از انتگرال مسیر فاینمن نشات می گیرد که در آن همه مسیرها از نقطه اولیه تا پایانی در فضازمان با یک فاکتور فاز مناسب کمک می کنند . انتگرال مسیر فاینمن را می توان از گسترش انتشار دهنده با استفاده از روشی به نام برش زمانی، [ 17 ] که در آن زمان گسسته می شود، انگیزه داد.

در مسیرهای غیر همتوپی، نمی توان از هر نقطه در یک برش زمانی به نقطه دیگری در برش زمانی بعدی رسید. این به این معنی است که می‌توانیم کلاس هم‌ارزی مسیرها را دارای فاکتورهای وزنی متفاوتی در نظر بگیریم . [ 18 ]

بنابراین می توان دریافت که مفهوم توپولوژیکی هم ارزی از مطالعه انتگرال مسیر فاینمن ناشی می شود . [ 16 ] : 28 

برای شفاف‌تر دیدن اینکه مفهوم هم‌ارزی «درست» است، به اثر آهارونوف-بوم مراجعه کنید .

آزمایش کنید

[ ویرایش ]

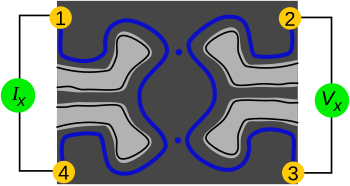
میکروگراف الکترونی روبشی تداخل سنج شبه ذره لافلین یک دستگاه نیمه هادی . چهار منطقه خاکستری روشن، دروازه های طلا و تیتانیم از الکترون های تخلیه نشده هستند . منحنی‌های آبی کانال‌های لبه‌ای از هم‌پتانسیل‌های این الکترون‌های تخلیه نشده هستند. منحنی‌های خاکستری تیره، ترانشه‌های حکاکی شده‌ای هستند که از الکترون‌ها تهی شده‌اند، نقاط آبی، اتصالات تونلی ، نقاط زرد، تماس‌های اهمی هستند . الکترون های دستگاه در یک صفحه 2 بعدی محدود می شوند. [ 19 ]

در سال 2020، دو تیم از دانشمندان (یکی در پاریس، دیگری در پوردو) شواهد تجربی جدیدی را برای وجود هریون اعلام کردند. هر دو آزمایش در شماره سالانه "وضعیت علم" مجله دیسکاور در سال 2020 ارائه شد . [ 2 ]

در آوریل 2020، محققان دانشگاه École normale supérieure (پاریس) و مرکز علوم نانو و فناوری نانو (C2N) نتایج یک "برخورد کننده ذرات" کوچک را برای هر کسی گزارش کردند. آن‌ها ویژگی‌هایی را شناسایی کردند که با پیش‌بینی‌های تئوری برای هر کسی مطابقت داشت. [ 1 ] [ 20 ] [ 21 ]

در ژوئیه 2020، دانشمندان دانشگاه پردو هر فردی را با استفاده از تنظیمات متفاوت شناسایی کردند. تداخل سنج این تیم الکترون ها را از طریق یک نانوساختار حکاکی شده پیچ و خم مانند ساخته شده از گالیم آرسنید و گالیم آرسنید آلومینیوم هدایت می کند . او گفت: «در مورد هر کسی ما، فاز تولید شده توسط قیطان 2π/3 بود. "این با آنچه قبلاً در طبیعت دیده شده متفاوت است." [ 22 ] [ 23 ]

از سال 2023، این حوزه تحقیقاتی فعال باقی مانده است. هوش مصنوعی کوانتومی گوگل با استفاده از یک پردازنده ابررسانا، در مقاله‌ای در arXiv توسط اندرسن و همکارانش، اولین بافته شدن ذرات غیرآبلی را گزارش کرد . در اکتبر 2022، [ 24 ] بعداً در Nature منتشر شد. [ 25 ] در مقاله‌ای در arXiv که در می 2023 منتشر شد، Quantinuum در مورد قیطاندن غیرآبلین با استفاده از یک پردازنده یون به دام افتاده گزارش داد. [ 26 ]

افراد غیر ابلی

[ ویرایش ]

مسئله حل نشده در فیزیک :

آیا نظم توپولوژیکی در دمای غیر صفر پایدار است ؟

(مسائل حل نشده بیشتر در فیزیک)

در سال 1988، Jürg Fröhlich نشان داد که تحت قضیه آمار اسپین معتبر است که مبادله ذرات یکنوید باشد (آمار غیرآبلی). [ 27 ] به طور خاص، این می تواند زمانی به دست آید که سیستم مقداری انحطاط را نشان دهد، به طوری که چندین حالت متمایز از سیستم دارای پیکربندی یکسانی از ذرات باشند. سپس تبادل ذرات می تواند نه تنها به تغییر فاز کمک کند، بلکه می تواند سیستم را با همان پیکربندی ذرات به حالتی متفاوت بفرستد. تبادل ذرات سپس با یک تبدیل خطی در این زیرفضای حالات منحط مطابقت دارد. وقتی انحطاط وجود ندارد، این زیرفضا یک بعدی است و بنابراین همه این تبدیل های خطی جابجا می شوند (زیرا آنها فقط ضرب در یک فاکتور فاز هستند). وقتی انحطاط وجود داشته باشد و این زیرفضا بعد بالاتری داشته باشد، این تبدیل های خطی نیازی به جابجایی ندارند (همانطور که ضرب ماتریس ندارد).

گرگوری مور ، نیکلاس رید و شیائو گانگ ون اشاره کردند که آمار غیر آبلی را می توان در اثر هال کوانتومی کسری (FQHE) درک کرد. [ 28 ] [ 29 ] در حالی که در ابتدا هرانیون های غیرآبلین عموماً یک کنجکاوی ریاضی در نظر گرفته می شدند، فیزیکدانان زمانی که الکسی کیتایف نشان داد که هرانیون های غیرآبلین را می توان برای ساخت یک کامپیوتر کوانتومی توپولوژیکی استفاده کرد، به سمت کشف خود حرکت کردند . از سال 2012، هیچ آزمایشی وجود هریون غیرآبلین را به طور قطعی نشان نداده است، اگرچه نکات امیدوارکننده‌ای در مطالعه وضعیت ν = 5/2 FQHE در حال ظهور است. [ نیاز به به روز رسانی ] [ 30 ] [ 31 ] شواهد تجربی از افراد غیرآبلین، اگرچه هنوز قطعی نیست و در حال حاضر مورد بحث قرار گرفته است، [ 32 ] در اکتبر 2013 ارائه شد . نظم توپولوژیکی abelian و anyons روی یک پردازنده یونی به دام افتاده [ 26 ] و نمایش بافته شدن غیر آبلی رئوس نمودار در یک پردازنده ابررسانا [ 25 ]

تلفیقی از هر کسی

[ ویرایش ]

تقریباً به همان شکلی که دو فرمیون (مثلاً هر دو اسپین 1/2) را می توان با هم به عنوان یک بوزون مرکب (با اسپین کل در برهم نهی 0 و 1) مشاهده کرد ، دو یا چند آنیون با هم یک هریون مرکب را تشکیل می دهند. احتمالاً یک بوزون یا فرمیون). گفته می شود که کامپوزیت anyon حاصل آمیختگی اجزای آن است.

اگر​ن{\displaystyle N}هریک از افراد آبلیان یکسان با آمارهای فردیα{\displaystyle \alpha }( یعنی سیستم یک فاز را انتخاب می کندهمنα{\displaystyle e^{i\alpha }}هنگامی که دو فرد منفرد تحت مبادله آدیاباتیک در خلاف جهت عقربه‌های ساعت قرار می‌گیرند) همه با هم ترکیب می‌شوند، با هم آماری دارند .ن2α{\displaystyle N^{2}\alpha }. ​این را می‌توان با توجه به این نکته مشاهده کرد که با چرخش خلاف جهت عقربه‌های ساعت دو آنیون مرکب در اطراف یکدیگر، ⁠ن2{\displaystyle N^{2}}جفت آنیون انفرادی (یکی در هر انیون مرکب اول، یکی در هرییون مرکب دوم) که هر کدام یک فاز دارند .همنα{\displaystyle e^{i\alpha }}. ​یک تحلیل مشابه برای ادغام آنیون های آبلی غیر یکسان اعمال می شود. آمار هر کامپوزیت به طور منحصر به فردی توسط آمار اجزای آن تعیین می شود.

افراد غیر آبلی روابط همجوشی پیچیده تری دارند. به عنوان یک قاعده، در یک سیستم با هریون های غیرآبلین، یک ذره مرکب وجود دارد که برچسب آماری آن به طور منحصر به فرد توسط برچسب های آماری اجزای آن تعیین نمی شود، بلکه به عنوان یک برهم نهی کوانتومی وجود دارد (این کاملا مشابه دو فرمیون شناخته شده است. برای داشتن اسپین 1/2 با هم در برهم نهی کوانتومی اسپین کل 1 و 0 هستند). اگر آمار کلی از همجوشی همه آنیون ها مشخص باشد، هنوز ابهام در ترکیب برخی از زیر مجموعه های آن آنیون ها وجود دارد و هر احتمال یک حالت کوانتومی منحصر به فرد است. این حالت‌های چندگانه فضای هیلبرت را فراهم می‌کنند که محاسبات کوانتومی را می‌توان روی آن انجام داد. [ 34 ]

مبنای توپولوژیکی

[ ویرایش ]

چرخش خلاف جهت عقربه های ساعت

چرخش در جهت عقربه های ساعت

تبادل دو ذره در فضازمان 2+1 با چرخش. چرخش‌ها نامتعادل هستند، زیرا نمی‌توان یکی را به دیگری تغییر شکل داد (بدون خروج خطوط جهان از هواپیما، در فضای دو بعدی غیرممکن است).

در بیش از دو بعد، قضیه آمار اسپین بیان می‌کند که هر حالت چندذره‌ای از ذرات غیرقابل تشخیص باید از آمار بوز-انیشتین یا فرمی دیراک تبعیت کند. برای هر d > 2، گروه های Lie SO( d ,1) (که گروه لورنتس را تعمیم می دهد ) و پوانکاره( d ,1) Z 2 را به عنوان اولین گروه هموتوپی خود دارند . از آنجا که گروه حلقوی Z 2 از دو عنصر تشکیل شده است، تنها دو احتمال باقی می ماند. (جزئیات بیشتر از این درگیر هستند، اما این نکته بسیار مهم است.)

وضعیت در دو بعد تغییر می کند. در اینجا اولین گروه هموتوپی SO(2،1)، و همچنین پوانکاره (2،1)، Z (دوره ای بی نهایت) است. این بدان معنی است که Spin(2,1) پوشش جهانی نیست : به سادگی متصل نیست . به طور جزئی، نمایش‌هایی از گروه متعامد خاص SO(2،1) وجود دارد که از نمایش‌های خطی SO(2،1) یا پوشش دوگانه آن ، گروه اسپین (2،1) ناشی نمی‌شوند . Anyon ها به طور مساوی نمایش های مکمل قطبش اسپین توسط یک ذره باردار هستند.

این مفهوم در مورد سیستم های غیر نسبیتی نیز صدق می کند. بخش مربوطه در اینجا این است که گروه چرخش فضایی SO(2) دارای یک گروه هموتوپی اول بی نهایت است.

این واقعیت همچنین مربوط به گروه های قیطانی است که در نظریه گره شناخته شده اند . این رابطه زمانی قابل درک است که این واقعیت را در نظر بگیریم که در دو بعد، گروه جایگشت دو ذره دیگر گروه متقارن S 2 (با دو عنصر) نیست ، بلکه گروه قیطان B2 ( با تعداد نامتناهی عنصر) است. نکته اساسی این است که یک قیطان می‌تواند به دور دیگری بپیچد، عملیاتی که می‌تواند به دفعات بی‌نهایت و در جهت عقربه‌های ساعت و همچنین در خلاف جهت عقربه‌های ساعت انجام شود.

یک رویکرد بسیار متفاوت برای مسئله پایداری-ناپیوستگی در محاسبات کوانتومی ، ایجاد یک کامپیوتر کوانتومی توپولوژیکی با آنیون‌ها، شبه ذرات مورد استفاده به عنوان رشته‌ها و تکیه بر نظریه braid برای تشکیل گیت‌های منطقی کوانتومی پایدار است . [ 35 ] [ 36 ]

تعمیم به ابعاد بالاتر

[ ویرایش ]

برانگیختگی های تکه تکه شده به عنوان ذرات نقطه ای می توانند بوزون، فرمیون یا هریون در ابعاد فضا-زمان 2+1 باشند. مشخص است که ذرات نقطه ای فقط می توانند بوزون یا فرمیون در ابعاد فضازمان 3+1 و بالاتر باشند. با این حال، برانگیختگی‌های حلقه‌ای (یا رشته‌ای) یا غشایی، اشیاء گسترده‌ای هستند که می‌توانند آماری جزئی داشته باشند.

تحقیقات کنونی نشان می‌دهد که برانگیختگی‌های حلقه‌ای و ریسمانی برای نظم‌های توپولوژیکی در فضازمان بعدی ۳+۱ وجود دارد، و آمارهای چند حلقه‌ای/رشته‌بافندگی آن‌ها نشانه‌های کلیدی برای شناسایی نظم‌های توپولوژیکی ۳+۱ بعدی است. [ 37 ] [ 38 ] [ 39 ] آمارهای چند حلقه/رشته بافته نظم های توپولوژیکی 3+1 بعدی را می توان با تغییر ناپذیر پیوند نظریه های میدان کوانتومی توپولوژیکی خاص در 4 بعد فضا-زمان بدست آورد. [ 39 ] به روش محاوره‌ای توضیح داده شده، اجسام گسترش‌یافته (حلقه، رشته، یا غشاء و غیره) می‌توانند به طور بالقوه هر یونیک در ابعاد فضا-زمان 3+1 و بالاتر در سیستم‌های درهم‌تنیده دوربرد باشند .

https://en.wikipedia.org/wiki/Anyon