3-اتساع زمان
اشتقاق و فرمول
[ ویرایش ]
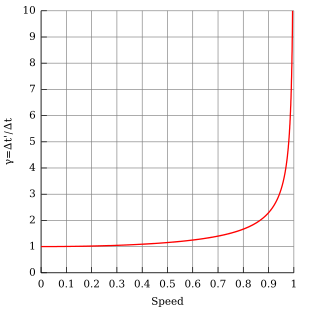
عامل لورنتس به عنوان تابعی از سرعت (در واحدهای طبیعی که c = 1). توجه کنید که برای سرعت های کوچک (از آنجایی که v به صفر میل می کند)، γ تقریباً 1 است.
علاوه بر ساعت نور استفاده شده در بالا، فرمول اتساع زمان را می توان به طور کلی از بخش زمانی تبدیل لورنتس استخراج کرد . [ 28 ] بگذارید دو رویداد وجود داشته باشد که ساعت متحرک آن را نشان می دهد

از آنجایی که ساعت در قاب اینرسی خود در حالت سکون باقی می ماند، به دنبال آن است

که در آن Δt فاصله زمانی بین دو رویداد همزمان (یعنی در یک مکان اتفاق میافتد) برای یک ناظر در یک قاب اینرسی است (مثلاً تیکهای ساعتش) که به عنوان زمان مناسب شناخته میشود ، Δ t' فاصله زمانی بین همان رویدادها، همانطور که توسط ناظر دیگری اندازه گیری شد، به طور اینرسی با سرعت v نسبت به ناظر قبلی حرکت می کند، v سرعت نسبی بین ناظر و ساعت متحرک است، c سرعت نور است، و فاکتور لورنتس (که به طور معمول با حرف یونانی گاما یا γ نشان داده می شود) عبارت است از:
بنابراین مدت زمان چرخه ساعت یک ساعت متحرک افزایش یافته است: اندازه گیری می شود که "آهسته کار می کند". دامنه چنین واریانس هایی در زندگی معمولی، جایی که v≪c ، حتی با در نظر گرفتن سفر فضایی ، به اندازه کافی بزرگ نیست که اثرات اتساع زمانی به راحتی قابل تشخیص باشد و چنین اثرات ناپدید کننده کوچکی را می توان با خیال راحت برای بیشتر اهداف نادیده گرفت. به عنوان یک آستانه تقریبی، اتساع زمانی ممکن است زمانی مهم شود که یک جسم به سرعتی در حدود 30000 کیلومتر بر ثانیه (1/10 سرعت نور) نزدیک شود. [ 29 ]
حرکت هایپربولیک
[ ویرایش ]
نوشتار اصلی: حرکت هایپربولیک (نسبیت)
در نسبیت خاص، اتساع زمانی در شرایطی که سرعت نسبی بدون تغییر است، به سادگی توصیف میشود. با این وجود، معادلات لورنتس به فرد اجازه میدهد زمان و حرکت مناسب در فضا را برای حالت ساده یک سفینه فضایی که با نیرویی در واحد جرم، نسبت به جسم مرجع در حرکت یکنواخت (یعنی سرعت ثابت)، معادل g در سرتاسر زمین اعمال میشود، محاسبه کند. دوره اندازه گیری
اجازه دهید t زمان در یک قاب اینرسی باشد که متعاقباً قاب استراحت نامیده می شود. اجازه دهید x یک مختصات فضایی باشد و اجازه دهید جهت شتاب ثابت و همچنین سرعت سفینه فضایی (نسبت به قاب استراحت) موازی با محور x باشد . با فرض اینکه موقعیت سفینه فضایی در زمان t = 0 x = 0 باشد و سرعت آن v 0 باشد و مخفف زیر را تعریف کنید:
فرمول های زیر برقرار است: [ 30 ]
موقعیت:
سرعت:
زمان مناسب به عنوان تابع زمان مختصات:
در موردی که v (0) = v 0 = 0 و τ (0) = τ 0 = 0، انتگرال را می توان به عنوان یک تابع لگاریتمی یا به طور معادل، به عنوان یک تابع هذلولی معکوس بیان کرد :
به عنوان توابع زمان مناسبτ
موقعیت:
سرعت:
هماهنگ کردن زمان به عنوان تابع زمان مناسب:
فرضیه ساعت
[ ویرایش ]
فرضیه ساعت این فرض است که سرعت یک ساعت تحت تأثیر اتساع زمانی به شتاب آن بستگی ندارد بلکه فقط به سرعت آنی آن بستگی دارد. این معادل بیان این است که یک ساعت در یک مسیر حرکت می کند
فرضیه ساعت به طور ضمنی (اما نه به طور صریح) در فرمول اولیه نسبیت خاص انیشتین در سال 1905 گنجانده شد. از آن زمان، این یک فرض استاندارد شده است و معمولاً در بدیهیات نسبیت خاص گنجانده شده است، به ویژه در پرتو تأیید تجربی تا شتاب های بسیار بالا در شتاب دهنده های ذرات . [ 32 ] [ 33 ]
اتساع زمان ناشی از گرانش یا شتاب
[ ویرایش ]
مقاله اصلی: اتساع زمان گرانشی
اتساع زمان توضیح می دهد که چرا دو ساعت کار پس از شتاب های مختلف زمان های متفاوتی را گزارش می دهند. برای مثال، زمان در ایستگاه فضایی بینالمللی کندتر میشود و به ازای هر 12 ماه زمینی که میگذرد، تقریباً 0.01 ثانیه تأخیر دارد. برای اینکه ماهوارههای جیپیاس کار کنند، باید خمشهای مشابه فضازمان را تنظیم کنند تا بهدرستی با سیستمهای روی زمین هماهنگ شوند. [ 2 ]
همانطور که در مورد اجرام عظیم (مانند زمین) مشاهده می شود، زمان با سرعت بیشتری از مرکز ثقل می گذرد.
اتساع زمان گرانشی توسط ناظری تجربه میشود که در ارتفاع معینی در یک چاه پتانسیل گرانشی، متوجه میشود که ساعتهای محلی آنها زمان سپری شده کمتری نسبت به ساعتهای یکسانی که در ارتفاع بالاتر قرار دارند (و در نتیجه در پتانسیل گرانشی بالاتری هستند) اندازهگیری میکنند.
اتساع زمان گرانشی به عنوان مثال برای فضانوردان ایستگاه فضایی بین المللی. در حالی که سرعت نسبی فضانوردان زمان آنها را کاهش می دهد، کاهش نفوذ گرانشی در مکان آنها سرعت آن را افزایش می دهد، هرچند به میزان کمتر. همچنین، زمان یک کوهنورد از نظر تئوری در بالای یک کوه در مقایسه با افراد در سطح دریا کمی سریعتر می گذرد. همچنین محاسبه شده است که به دلیل اتساع زمانی، هسته زمین 2.5 سال جوانتر از پوسته است . [ 34 ] "ساعتی که برای زمانبندی چرخش کامل زمین استفاده میشود، روز را تقریباً 10 ns/روز بیشتر برای هر کیلومتر از ارتفاع بالای ژئوئید مرجع اندازهگیری میکند." [ 35 ] سفر به مناطقی از فضا که در آن اتساع زمان گرانشی شدید اتفاق میافتد، مانند نزدیک (اما نه فراتر از افق رویداد ) یک سیاهچاله ، میتواند نتایج تغییر زمان مشابه نتایج سفرهای فضایی با سرعت نزدیک به نور را به همراه داشته باشد.
بر خلاف اتساع زمان سرعت، که در آن هر دو ناظر دیگری را با پیری کندتر اندازه گیری می کنند (یک اثر متقابل)، اتساع زمان گرانشی متقابل نیست. این بدان معناست که با اتساع زمان گرانشی، هر دو ناظر موافق هستند که ساعت نزدیکتر به مرکز میدان گرانشی سرعت کمتری دارد، و آنها بر روی نسبت اختلاف توافق دارند.














 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.