3-میدانهای متناهی GF(2^ n )
جدول 4.7 محاسبه معکوس ضربی ( x 7 + x + 1) mod ( x 8 + x 4 + x 3 + x + 1) را نشان می دهد. نتیجه این است که ( x 7 + x + 1) 1 = ( x 7 ). یعنی ( x 7 + x + 1) ( x 7 )
|
ملاحظات محاسباتی
یک چند جمله ای f ( x ) در GF( 2n )
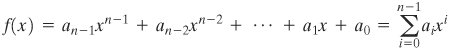
را می توان به طور منحصر به فرد با n ضرایب باینری آن ( a n 1 a n 2 ... a 0 ) نشان داد. بنابراین، هر چند جمله ای در GF( 2n ) را می توان با یک عدد n بیتی نشان داد.
[صفحه 125]
جداول 4.5 و 4.6 جداول جمع و ضرب را برای GF(2 3 ) مدول m ( x ) = ( x 3 + x + 1) نشان می دهد. جدول 4.5 از نمایش باینری و جدول 4.6 از نمایش چند جمله ای استفاده می کند. |
اضافه شدن
دیدیم که جمع چندجمله ای ها با جمع ضرایب متناظر انجام می شود و در مورد چندجمله ای های بیش از Z 2 جمع فقط عمل XOR است. بنابراین، جمع دو چند جمله ای در GF( 2n ) مربوط به عملیات XOR بیتی است.
دو چند جمله ای را در GF(2 8 ) از مثال قبلی ما در نظر بگیرید: f ( x ) = x 6 + x 4 + x 2 + x + 1 و g ( x ) = x 7 + x + 1.
|
ضرب
هیچ عملیات XOR ساده ای وجود ندارد که ضرب را در GF(2 n ) انجام دهد، با این حال، یک تکنیک نسبتاً ساده و به راحتی قابل پیاده سازی در دسترس است. ما این تکنیک را با ارجاع به GF(2 8 ) با استفاده از m ( x ) = x 8 + x 4 + x 3 + x + 1 مورد بحث قرار خواهیم داد، که میدان محدود مورد استفاده در AES است. این تکنیک به راحتی به GF( 2n ) تعمیم می یابد.
این تکنیک بر اساس مشاهده است که
معادله 4-8
![]()
[صفحه 126]
یک لحظه فکر باید شما را متقاعد کند که معادله (4.8) درست است. اگر نه، آن را تقسیم کنید. به طور کلی، در GF(2 n ) با یک چند جمله ای درجه n ام p ( x )، x n mod p ( x ) = [ p ( x ) x n ] داریم.
حال، چند جمله ای را در GF(2 8 ) در نظر بگیرید که به شکل f ( x ) = b 7 x 7 + b 6 x 6 + b 5 x 5 + b 4 x 4 + b 3 x 3 + b 2 x 2 است. + b 1 x + b 0 . اگر در x ضرب کنیم، داریم
معادله 4-9
![]()
اگر b 7 = 0، نتیجه یک چند جمله ای با درجه کمتر از 8 است که در حال حاضر به شکل کاهش یافته است و نیازی به محاسبه بیشتر نیست. اگر b 7 = 1، مدول کاهش m ( x ) با استفاده از رابطه (4.8) به دست می آید:
x x f ( x ) = ( b 6 x 7 + b 5 x 6 + b 4 x 5 + b 3 x 4 + b 2 x 3 +
b 1 x 2 + b 0 x ) + ( x 4 + x 3 + x + 1)
نتیجه می شود که ضرب در x (یعنی 00000010) می تواند به صورت یک شیفت چپ 1 بیتی و به دنبال آن یک XOR بیتی شرطی با (00011011) پیاده سازی شود که نشان دهنده ( x 4 + x 3 + x + 1) است. به طور خلاصه،
معادله 4-10
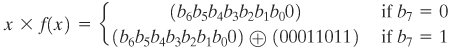
ضرب در توان بالاتر x را می توان با اعمال مکرر معادله (4.10) به دست آورد. با افزودن نتایج میانی، ضرب در هر ثابت در GF(2 8 ) میتوان به دست آورد.
در مثال قبلی نشان دادیم که برای f ( x ) = x 6 + x 4 + x 2 + x + 1، g ( x ) = x 7 + x + 1، و m ( x ) = x 8 + x 4 + x 3 + x + 1، f ( x ) x g ( x ) mod m ( x ) = x 7+ x 6 + 1. با انجام مجدد این کار در حساب باینری، باید (01010111) x (10000011) را محاسبه کنیم. ابتدا نتایج حاصل از ضرب در توان های x را تعیین می کنیم : (01010111) x (00000001) = (10101110) (01010111) x (00000100) = (01011100) (01010111) x (00001000) = (10001110) (01010111) x (00010000) = (00011100) (01010111) x (00100000) = (00001110) (01010111) x (01000000) = (00011100) (01010111) x (10000000) = (00111000) بنابراین، (01010111) x (10000011) = (01010111) x [(00000001) x (00000010) x (10000000)] = (01010111) که معادل x 7 + x 6 + 1 است. |
[صفحه 127]
استفاده از ژنراتور
یک تکنیک معادل برای تعریف یک میدان محدود به شکل GF( 2n ) با استفاده از همان چند جملهای تقلیلناپذیر، گاهی راحتتر است. برای شروع، ما به دو تعریف نیاز داریم: یک مولد g از یک میدان محدود F مرتبه q (شامل عناصر q ) عنصری است که اولین قدرتهای q 1 آن تمام عناصر غیر صفر F را تولید می کند. یعنی عناصر F از 0 تشکیل شده است. , g 0 , g 1 ,..., g q 2 . یک فیلد F را در نظر بگیرید که با یک چند جمله ای f ( x ) تعریف شده است. عنصر b موجود در F ریشه نامیده می شوداز چند جمله ای اگر f ( b ) = 0 باشد. در نهایت، می توان نشان داد که یک ریشه g از یک چند جمله ای تقلیل ناپذیر، مولد میدان متناهی است که روی آن چند جمله ای تعریف شده است.
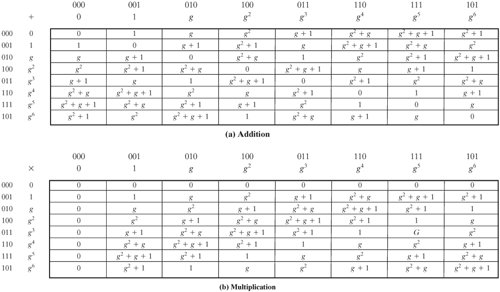
اجازه دهید میدان محدود GF(23) را در نظر بگیریم ، که بر روی چند جمله ای تقلیل ناپذیر x 3 + x + 1 تعریف شده است، که قبلاً بحث شد. بنابراین، مولد g باید f ( x ) = g 3 + g + 1 = 0 را برآورده کند. همانطور که قبلاً بحث شد، به خاطر داشته باشید که ما نیازی به یافتن یک راه حل عددی برای این برابری نداریم. بلکه با حساب چند جمله ای سروکار داریم که در آن محاسبات بر روی ضرایب مدول 2 انجام می شود. بنابراین، راه حل برابری قبلی g 3 = g 1 = g است.+ 1. اکنون نشان می دهیم که g در واقع همه چند جمله ای های درجه کمتر از 3 را تولید می کند. موارد زیر را داریم: g 4 = g ( g 3 ) = g ( g + 1) = g 2 + g g 5 = g ( g 4 ) = g ( g 2 + g ) = g 3 + g 2 = g 2 + g + 1 g 6 = g ( g 5 ) = g ( g 2 + g + 1 ) = g 3 + g 2 + g = g 2 + g + g + 1 = g 2 + 1 g 7 = g ( g 6 ) = g ( g 2 + 1) = g 3 + g = g + g + 1 = 1 = g 0 می بینیم که توان های g همه چند جمله ای های غیر صفر را در GF(2 3 ) تولید می کنند. همچنین، باید واضح باشد که g k = g k mod 7 برای هر عدد صحیح k . جدول 4.8 نمایش توان و همچنین نمایش های چند جمله ای و باینری را نشان می دهد.
این نمایش قدرت ضرب را آسان می کند. برای ضرب در نماد قدرت، نماهای مدول 7 را اضافه کنید. به عنوان مثال، g 4 x g 6 = g (10 mod 7) = g 3 = g + 1. همین نتیجه با استفاده از حساب چند جمله ای به دست می آید، به صورت زیر: g داریم 4 = g 2 + g و g 6 = g 2 + 1. سپس، ( g 2 + g ) x ( g 2 + 1) = g 4 + g 3+ g 2 + 1. سپس باید ( g 4 + g 3 + g 2 + 1) mod ( g 3 + g + 1) را با تقسیم تعیین کنیم: [صفحه 129]
نتیجه g + 1 را دریافت می کنیم که با نتیجه به دست آمده با استفاده از نمایش قدرت مطابقت دارد. جدول 4.9 جداول جمع و ضرب را برای GF(2 3 ) با استفاده از نمایش توان نشان می دهد. توجه داشته باشید که این نتایج یکسان با نمایش چند جمله ای (جدول 4.6) با تعویض برخی از سطرها و ستون ها به دست می دهد.
جدول 4.9. GF(2 3 ) محاسبات با استفاده از مولد برای چند جمله ای ( x 3 + x + 1) (این مورد در نسخه چاپی صفحه 128 نمایش داده شده است)
|
به طور کلی، برای GF( 2n ) با چند جمله ای تقلیل ناپذیر f ( x )، g n = f ( x ) g n را تعیین کنید. سپس تمام توان های g را از g n +1 تا g 2 n 2 محاسبه کنید. عناصر میدان با توان های g از تا g 2 n 2 به اضافه مقدار 0 مطابقت دارد. برای ضرب دو عنصر در میدان، از برابری g k = g k mod استفاده کنید (2n 1)برای هر عدد صحیحk.
خلاصه
در این بخش نحوه ساخت یک میدان محدود از مرتبه 2 n را نشان دادیم . به طور خاص، ما GF(2 n ) را با ویژگی های زیر تعریف کردیم:
GF(2 n ) از 2 n عنصر تشکیل شده است.
عملیات باینری + و x بر روی مجموعه تعریف می شوند. عملیات جمع، تفریق، ضرب و تقسیم را می توان بدون خروج از مجموعه انجام داد. هر عنصر از مجموعه غیر از 0 دارای یک معکوس ضرب است.
ما نشان دادیم که عناصر GF( 2n ) را می توان به عنوان مجموعه ای از همه چند جمله ای های درجه n 1 یا کمتر با ضرایب باینری تعریف کرد. هر چند جمله ای از این قبیل را می توان با یک مقدار n بیت منحصر به فرد نشان داد. حساب به عنوان مدول حسابی چند جمله ای چند جمله ای غیر قابل تقلیل درجه n تعریف می شود. همچنین دیدهایم که تعریف معادل یک میدان محدود GF( 2n ) از یک مولد استفاده میکند و حساب با استفاده از توانهای مولد تعریف میشود.
https://flylib.com/books/en/3.190.1.50/1/
 1 (mod ( x 4 + x 3 + x + 1)).
1 (mod ( x 4 + x 3 + x + 1)). (10000011)
(10000011) (00011011) = (01000111)
(00011011) = (01000111)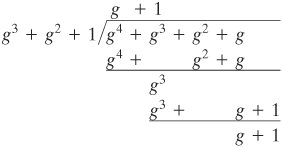
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.