پنهان شدن

فهرست

پنهان شدن

چرخه اتو

      از ویکیپدیا، دانشنامه آزاد

      همچنین ببینید: موتور اتو و موتور چهار زمانه

      ترمودینامیک

      موتور حرارتی کلاسیک کارنو

      نشان می دهد

      شاخه ها

      نشان می دهد

      قوانین

      نشان می دهد

      سیستم های

      نشان می دهد

      خصوصیات سیستم

      نشان می دهد

      خواص مواد

      نشان می دهد

      معادلات

      نشان می دهد

      پتانسیل ها

      نشان می دهد
      • تاریخ
      • فرهنگ
      نشان می دهد

      دانشمندان

      نشان می دهد

      دیگر

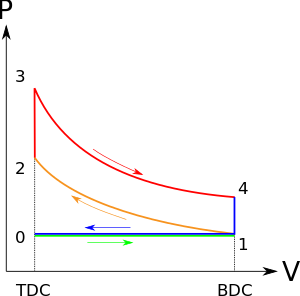
      نمودار فشار-حجم چرخه اتو نمودارهای ایده آل چرخه اتو چهار زمانه هر دو نمودار : سکته ورودی ( 0-1 و سبز رنگی) توسط یک انبساط ایزوباریک انجام می شود و به دنبال آن یک فشار آدیاباتیک ( 1-2 و نارنجی رنگی ) انجام می شود. . از طریق احتراق سوخت، گرما در یک فرآیند حجم ثابت ( فرآیند ایزوکوریک ) (2-3) و به دنبال آن یک روند انبساط آدیاباتیک (3-4 و قرمز رنگی ) اضافه می شود. چرخه با ضربه اگزوز (4-0 و آبی رنگی ) بسته می شود که با خنک سازی ایزوکوریک و فرآیندهای فشرده سازی ایزوباریک مشخص می شود.

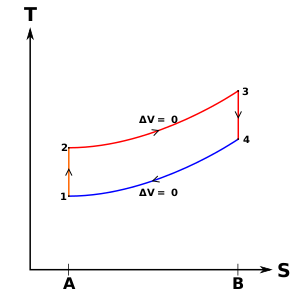
      نمودار دما- آنتروپی

      چرخه اتو یک چرخه ترمودینامیکی ایده آل است که عملکرد یک موتور پیستونی جرقه زنی معمولی را توصیف می کند . این چرخه ترمودینامیکی است که بیشتر در موتورهای خودرو یافت می شود. [1]

      چرخه اتو توصیفی از اتفاقاتی است که برای گاز در اثر تغییرات فشار، دما، حجم، افزودن گرما و حذف گرما روی می دهد. گازی که در معرض آن تغییرات قرار می گیرد سیستم نامیده می شود. سیستم، در این مورد، به عنوان سیال (گاز) درون سیلندر تعریف می شود. با تشریح تغییراتی که در داخل سیستم اتفاق می‌افتد، تأثیر سیستم بر محیط را نیز به صورت معکوس توصیف می‌کند. در مورد چرخه اتو، اثر آن تولید شبکه کافی از سیستم خواهد بود تا خودرو و سرنشینان آن را در محیط به حرکت درآورد.

      چرخه اتو از زیر ساخته شده است:

      بالا و پایین حلقه: یک جفت فرآیند شبه موازی و ایزنتروپیک (بدون اصطکاک، برگشت پذیر آدیاباتیک ).

      سمت چپ و راست حلقه: یک جفت فرآیند ایزوکوریک موازی (حجم ثابت).

      فرآیند ایزنتروپیک تراکم یا انبساط به این معنی است که هیچ ناکارآمدی (از دست دادن انرژی مکانیکی) وجود نخواهد داشت و در طی آن فرآیند انتقال گرما به داخل یا خارج از سیستم وجود نخواهد داشت. سیلندر و پیستون در این مدت در برابر حرارت غیرقابل نفوذ فرض می شوند. کار بر روی سیستم در طول فرآیند فشرده سازی ایزنتروپیک پایین انجام می شود. گرما از طریق فرآیند فشار دادن چپ به چرخه اتو جریان می یابد و مقداری از آن از طریق فرآیند کاهش فشار سمت راست به بیرون جریان می یابد. مجموع کار اضافه شده به سیستم به اضافه گرمای اضافه شده منهای گرمای حذف شده، کار مکانیکی خالص تولید شده توسط سیستم را به همراه دارد.

      فرآیندها [ ویرایش ]

      فرآیندها توسط: [2] شرح داده شده است:

      • فرآیند 0-1 یک توده هوا با فشار ثابت به آرایش پیستون/سیلندر کشیده می شود.
      • فرآیند 1-2 فشرده سازی آدیاباتیک (ایسنتروپیک) بار است که پیستون از نقطه مرگ پایین ( BDC ) به نقطه مرگ بالا ( TDC ) حرکت می کند.
      • فرآیند 2-3 انتقال حرارت با حجم ثابت به گاز در حال کار از یک منبع خارجی است در حالی که پیستون در نقطه مرگ بالا قرار دارد. این فرآیند برای نشان دادن احتراق مخلوط سوخت و هوا و سوختن سریع متعاقب آن در نظر گرفته شده است.
      • فرآیند 3-4 یک انبساط آدیاباتیک (ایسنتروپیک) (سکته قدرتی) است.
      • فرآیند 4-1 چرخه را با یک فرآیند با حجم ثابت تکمیل می کند که در آن گرما از هوا دفع می شود در حالی که پیستون در نقطه مرگ پایین قرار دارد.
      • فرآیند 1-0 جرم هوا در یک فرآیند فشار ثابت به اتمسفر آزاد می شود.

      چرخه اتو شامل فشرده سازی ایزنتروپیک، افزودن گرما در حجم ثابت، انبساط ایزنتروپیک و دفع گرما در حجم ثابت است. در مورد چرخه اتو چهار زمانه، از نظر فنی دو فرآیند اضافی وجود دارد: یکی برای خروج گرمای اتلاف و محصولات احتراق در فشار ثابت (ایزوباریک)، و دیگری برای جذب هوای خنک غنی از اکسیژن نیز در فشار ثابت. ; با این حال، این موارد اغلب در یک تحلیل ساده حذف می شوند. حتی اگر این دو فرآیند برای عملکرد یک موتور واقعی حیاتی هستند، که در آن جزئیات انتقال حرارت و شیمی احتراق مرتبط هستند، برای تجزیه و تحلیل ساده چرخه ترمودینامیکی، راحت‌تر فرض کنیم که تمام گرمای اتلاف در طول یک تغییر حجم حذف می شود.

      تاریخچه [ ویرایش ]

      موتور چهار زمانه برای اولین بار توسط Alphonse Beau de Rochas در سال 1861 به ثبت رسید . [3] قبل از آن، در حدود 1854-1857، دو ایتالیایی ( Eugenio Barsanti و Felice Matteucci ) موتوری را اختراع کردند که شایعه شده بود که بسیار شبیه است، اما حق ثبت اختراع گم شده بود. [ نیازمند منبع ]

      اولین کسی که یک موتور چهار زمانه کار کرد، یک موتور ثابت با استفاده از مخلوط زغال سنگ گاز و هوا برای سوخت (موتور گازی )، مهندس آلمانی نیکلاس اتو بود . [4] به همین دلیل است که اصل چهار زمانه امروزه معمولاً به عنوان چرخه اتو شناخته می شود و موتورهای چهار زمانه با استفاده از شمع اغلب موتورهای اتو نامیده می شوند.

      فرآیندها [ ویرایش ]

      چرخه دارای چهار بخش است: جرمی حاوی مخلوطی از سوخت و اکسیژن توسط پیستون نزولی به داخل سیلندر کشیده می شود، با بالا آمدن پیستون فشرده می شود، جرم توسط جرقه ای مشتعل می شود که انرژی را به شکل گرما آزاد می کند، و در نتیجه آن به وجود می آید. گاز با فشار دادن پیستون به پایین اجازه انبساط پیدا می کند و در نهایت با بالا آمدن پیستون برای بار دوم جرم تخلیه می شود. از آنجایی که پیستون قادر به حرکت در امتداد سیلندر است، حجم گاز با موقعیت آن در سیلندر تغییر می کند. فرآیندهای فشرده‌سازی و انبساط ناشی از حرکت پیستون بر روی گاز به‌عنوان برگشت‌پذیر ایده‌آل می‌شوند، یعنی هیچ کار مفیدی از طریق اغتشاش یا اصطکاک از بین نمی‌رود و در طی این دو فرآیند هیچ گرمایی به گاز یا از گاز منتقل نمی‌شود. پس از اتمام انبساط در سیلندر، حرارت باقیمانده استخراج شده و در نهایت گاز به محیط خارج می شود. کار مکانیکی در طول فرآیند انبساط تولید می شود و مقداری از آن برای فشرده سازی توده هوا در چرخه بعدی استفاده می شود. کار مکانیکی تولید شده منهای مورد استفاده برای فرآیند فشرده سازی، کار خالص به دست آمده است و می تواند برای رانش یا راندن ماشین های دیگر استفاده شود. روش دیگر، کار خالص به دست آمده تفاوت بین گرمای تولید شده و گرمای حذف شده است.

      چرخه اتو

      فرآیند مصرف 0-1 (سایه آبی) [ ویرایش ]

      توده ای از هوا (سیال کار) از 0 تا 1 در فشار اتمسفر (فشار ثابت) از طریق دریچه ورودی باز به داخل سیلندر کشیده می شود، در حالی که دریچه خروجی در طی این فرآیند بسته می شود. دریچه ورودی در نقطه 1 بسته می شود.

      سکته فشرده سازی فرآیند 1-2 ( B در نمودارها) [ ویرایش ]

      پیستون از انتهای میل لنگ (BDC، نقطه مرده پایین و حداکثر حجم) به انتهای سرسیلندر ( TDC ، نقطه مرگ بالا و حداقل حجم) حرکت می کند، زیرا گاز کار با حالت اولیه 1 به صورت ایزنتروپیک به حالت 2، از طریق نسبت تراکم ( V) فشرده می شود. 1 / V 2 ) . از نظر مکانیکی، این فشرده‌سازی ایزنتروپیک مخلوط هوا/سوخت در سیلندر است که به آن ضربه فشرده‌سازی نیز می‌گویند. این فرآیند ایزنتروپیک فرض می‌کند که هیچ انرژی مکانیکی در اثر اصطکاک از بین نمی‌رود و هیچ گرمایی به گاز یا از گاز منتقل نمی‌شود، بنابراین فرآیند برگشت‌پذیر است. فرآیند تراکم مستلزم آن است که کار مکانیکی به گاز کار اضافه شود. به طور کلی نسبت تراکم در حدود 9-10:1 ( V 1 : V 2 ) برای یک موتور معمولی است. [5]

      مرحله احتراق فرآیند 2-3 ( C روی نمودارها) [ ویرایش ]

      پیستون به طور لحظه ای در TDC در حال استراحت است . در طول این لحظه، که به عنوان فاز اشتعال شناخته می شود، مخلوط هوا/سوخت در حجم کمی در بالای حرکت تراکم باقی می ماند. گرما با احتراق سوخت تزریق شده به سیال کار اضافه می شود و حجم آن اساساً ثابت می ماند. فشار افزایش می یابد و نسبت(پ3/پ2){\displaystyle (P_{3}/P_{2})}"نسبت انفجار" نامیده می شود.

      روند گسترش 3-4 ( D در نمودارها) [ ویرایش ]

      افزایش فشار بالا نیرویی به پیستون وارد می کند و آن را به سمت BDC هل می دهد . انبساط سیال عامل به صورت ایزنتروپیک صورت می گیرد و کار توسط سیستم روی پیستون انجام می شود. نسبت حجم{\displaystyle V_{4}/V_{3}}"نسبت انبساط ایسنتروپیک" نامیده می شود. (برای چرخه اتو همان نسبت تراکم است{\displaystyle V_{1}/V_{2}}). از نظر مکانیکی، این انبساط مخلوط گاز داغ در سیلندر است که به عنوان ضربه انبساط (قدرت) شناخته می شود.

      فرآیند 4-1 رد گرمای ایده آل ( A در نمودارها) [ ویرایش ]

      پیستون به طور لحظه ای در BDC در حال استراحت است . فشار گاز کار فوراً از نقطه 4 به نقطه 1 در طول یک فرآیند حجم ثابت کاهش می یابد زیرا گرما به یک سینک خارجی ایده آل که با سرسیلندر در تماس است خارج می شود. در موتورهای احتراق داخلی مدرن، هیت سینک ممکن است هوای اطراف (برای موتورهای کم توان)، یا یک سیال در گردش، مانند مایع خنک کننده باشد. گاز به حالت 1 بازگشته است.

      فرآیند 1-0 ضربه اگزوز [ ویرایش ]

      سوپاپ اگزوز در نقطه 1 باز می شود. همانطور که پیستون از "BDC" (نقطه 1) به "TDC" (نقطه 0) با دریچه اگزوز باز می شود، مخلوط گازی به اتمسفر تخلیه می شود و فرآیند از نو شروع می شود.

      تجزیه و تحلیل چرخه [ ویرایش ]

      در این فرآیند 1-2، پیستون روی گاز کار می کند و در فرآیند 3-4، گاز به ترتیب در طی فرآیندهای فشرده سازی و انبساط ایزنتروپیک روی پیستون کار می کند. فرآیندهای 2-3 و 4-1 فرآیندهای ایزوکوریک هستند. گرما از 2-3 به سیستم و از 4-1 به خارج از سیستم منتقل می شود اما در طی این فرآیندها هیچ کاری روی سیستم انجام نمی شود یا از سیستم استخراج می شود. هیچ کاری در طول یک فرآیند ایزوکوریک (حجم ثابت) انجام نمی شود زیرا اضافه یا حذف کار از یک سیستم مستلزم حرکت مرزهای سیستم است. از این رو، از آنجایی که حجم سیلندر تغییر نمی کند، هیچ شفت کاری به سیستم اضافه یا از آن حذف نمی شود.

      از چهار معادله مختلف برای توصیف آن چهار فرآیند استفاده می شود. با فرض اینکه تغییرات انرژی جنبشی و پتانسیلی که در سیستم اتفاق می‌افتد (جرم گاز) را می‌توان نادیده گرفت و سپس با اعمال قانون اول ترمودینامیک (پایستگی انرژی) بر جرم گاز با تغییر حالت طبق مشخصه، ساده‌سازی انجام می‌شود. توسط دما، فشار و حجم گاز. [2] [ صفحه مورد نیاز ] [6] [ صفحه مورد نیاز ]

      در طی یک چرخه کامل، گاز به حالت اولیه خود یعنی دما، فشار و حجم باز می گردد، بنابراین تغییر انرژی خالص داخلی سیستم (گاز) صفر است. در نتیجه، انرژی (گرما یا کار) اضافه شده به سیستم باید با انرژی (گرما یا کاری) که از سیستم خارج می شود جبران شود. در تجزیه و تحلیل سیستم های ترمودینامیکی، قرارداد این است که انرژی ورودی به سیستم مثبت و انرژی خروجی از سیستم منفی در نظر گرفته شود.

      معادله 1a.

      در طول یک چرخه کامل، تغییر خالص انرژی سیستم صفر است:

      {\displaystyle \Delta E=E_{\text{in}}-E_{\text{out}}=0}

      در بالا بیان می شود که سیستم (جرم گاز) به حالت ترمودینامیکی اولیه ای که در شروع چرخه در آن بود باز می گردد.

      جایی که{\displaystyle E_{\text{in}}}انرژی از 1-2-3 و به سیستم اضافه می شود{\displaystyle E_{\text{out}}}انرژی از سیستم 3-4-1 حذف می شود. از نظر کار و حرارت اضافه شده به سیستم

      معادله 1b:

      {\displaystyle W_{1-2}+Q_{2-3}+W_{3-4}+Q_{4-1}=0}

      هر جمله از معادله را می توان بر حسب انرژی داخلی گاز در هر نقطه از فرآیند بیان کرد:

      {\displaystyle W_{1-2}=U_{2}-U_{1}}

      {\displaystyle Q_{2-3}=U_{3}-U_{2}}

      {\displaystyle W_{3-4}=U_{4}-U_{3}}

      {\displaystyle Q_{4-1}=U_{1}-U_{4}}

      تعادل انرژی معادله 1b می شود

      {\displaystyle W_{1-2}+Q_{2-3}+W_{3-4}+Q_{4-1}=\left(U_{2}-U_{1}\right)+\left( U_{3}-U_{2}\right)+\left(U_{4}-U_{3}\right)+\left(U_{1}-U_{4}\right)=0}

      برای نشان دادن مثال، مقداری [ مشکوک – بحث ] را برای نقاط در تصویر انتخاب می کنیم:

      {\displaystyle U_{1}=1}

      {\displaystyle U_{2}=5}

      {\displaystyle U_{3}=9}

      {\displaystyle U_{4}=4}

      این مقادیر به طور دلخواه اما منطقی [ مشکوک – بحث ] انتخاب شده اند. سپس شرایط کار و گرما را می توان محاسبه کرد.

      انرژی اضافه شده به سیستم به عنوان کار در طول فشرده سازی از 1 تا 2 است

      {\displaystyle \left(U_{2}-U_{1}\right)=\left(5-1\right)=4}

      انرژی اضافه شده به سیستم به عنوان گرما از نقطه 2 تا 3 است

      {\displaystyle \left({U_{3}-U_{2}}\right)=\left(9-5\right)=4}

      انرژی خارج شده از سیستم به عنوان کار در طول انبساط از 3 به 4 است

      {\displaystyle \left(U_{4}-U_{3}\right)=\left(4-9\right)=-5}

      انرژی خارج شده از سیستم به عنوان گرما از نقطه 4 تا 1 است

      {\displaystyle \left(U_{1}-U_{4}\right)=\left(1-4\right)=-3}

      تعادل انرژی است

      {\displaystyle \Delta E=+4+4-5-3=0}

      توجه داشته باشید که انرژی اضافه شده به سیستم به عنوان مثبت و انرژی خروجی از سیستم منفی محاسبه می شود و جمع صفر است همانطور که انتظار می رود برای یک چرخه کامل که سیستم را به حالت اولیه باز می گرداند.

      از تعادل انرژی، کار خارج از سیستم عبارت است از:

      {\displaystyle \sum {\text{Work}}=W_{1-2}+W_{3-4}=\left(U_{2}-U_{1}\right)+\left(U_{4} -U_{3}\right)=4-5=-1}

      انرژی خالص خروجی از سیستم به عنوان کار 1- است، به این معنی که سیستم یک واحد خالص انرژی تولید کرده است که به صورت کار از سیستم خارج می شود.

      گرمای خالص خروجی از سیستم عبارت است از:

      {\displaystyle \sum {\text{Heat}}=Q_{2-3}+Q_{4-1}=\left(U_{3}-U_{2}\right)+\left(U_{1} -U_{4}\right)=4-3=1}

      به عنوان انرژی اضافه شده به سیستم به عنوان گرما مثبت است. از موارد فوق به نظر می رسد که سیستم یک واحد گرما به دست آورده است. این با انرژی تولید شده توسط سیستم به عنوان کار خارج از سیستم مطابقت دارد.

      راندمان حرارتی ضریب کار خالص از سیستم به گرمای اضافه شده به سیستم است. معادله 2:

      {\displaystyle \eta ={\frac {W_{1-2}+W_{3-4}}{Q_{2-3}}}={\frac {\left(U_{2}-U_{1} \right)+\left(U_{4}-U_{3}\right)}{\left(U_{3}-U_{2}\right)}}}

      {\displaystyle \eta =1+{\frac {U_{1}-U_{4}}{\left(U_{3}-U_{2}\right)}}=1+{\frac {(1- 4)}{(9-5)}}=0.25}

      روش دیگر، راندمان حرارتی را می توان با گرمای شدید اضافه شده و گرما رد کرد بدست آورد.

      {\displaystyle \eta ={\frac {Q_{2-3}+Q_{4-1}}{Q_{2-3}}}=1+{\frac {\left(U_{1}-U_{ 4}\right)}{\left(U_{3}-U_{2}\right)}}}

      ارائه ارزش های ساختگی

      {\displaystyle \eta =1+{\frac {1-4}{9-5}}=1+{\frac {-3}{4}}=0.25}

      در چرخه اتو، هیچ انتقال حرارتی در طول فرآیند 1-2 و 3-4 وجود ندارد زیرا آنها فرآیندهای ایزنتروپیک هستند. گرما فقط در طول فرآیندهای حجم ثابت 2-3 تامین می شود و گرما فقط در طول فرآیندهای حجم ثابت 4-1 رد می شود.

      مقادیر فوق مقادیر مطلقی هستند که ممکن است، برای مثال [ مشکوک - بحث ] ، دارای واحدهای ژول باشند (با فرض اینکه سیستم واحدهای MKS استفاده شود) و برای یک موتور خاص با ابعاد خاص کاربرد دارند. در مطالعه سیستم‌های ترمودینامیکی، مقادیر گسترده‌ای مانند انرژی، حجم، یا آنتروپی (در مقابل مقادیر شدید دما و فشار) بر اساس جرم واحد قرار می‌گیرند، و همچنین محاسبات نیز همین‌طور است، که آن‌ها را کلی‌تر و در نتیجه کلی‌تر می‌کند. استفاده کنید. از این رو، هر عبارتی که شامل یک کمیت گسترده است را می توان بر جرم تقسیم کرد و واحدهای ژول/کیلوگرم ( انرژی ویژه )، متر 3 /کیلوگرم (حجم خاص)، یا ژول/(کلوین· کیلوگرم) (آنتروپی خاص، گرما) را به دست داد. ظرفیت) و غیره و با استفاده از حروف کوچک، u، v، s و غیره نشان داده می شود.

      اکنون می توان معادله 1 را با معادله گرمای ویژه برای حجم ثابت مرتبط کرد. گرمای ویژه به ویژه برای محاسبات ترمودینامیکی که شامل مدل گاز ایده آل است مفید هستند .

      {\displaystyle C_{\text{v}}=\left({\frac {\delta u}{\delta T}}\right)_{\text{v}}}

      بازآرایی بازده:

      {\displaystyle \delta u=(C_{\text{v}})(\delta T)}

      درج معادله گرمای ویژه در معادله بازده حرارتی (معادله 2) نتیجه می دهد.

      {\displaystyle \eta =1-\left({\frac {C_{\text{v}}(T_{4}-T_{1})}{C_{\text{v}}(T_{3}- T_{2})}}\راست)}

      پس از تنظیم مجدد:

      {\displaystyle \eta =1-\left({\frac {T_{1}}{T_{2}}}\right)\left({\frac {T_{4}/T_{1}-1}{ T_{3}/T_{2}-1}}\راست)}

      در مرحله بعد، از نمودارها توجه کنید{\displaystyle T_{4}/T_{1}=T_{3}/T_{2}}(به روابط ایزنتروپیک برای گاز ایده آل مراجعه کنید )، بنابراین هر دوی اینها را می توان حذف کرد. سپس معادله به زیر کاهش می یابد:

      معادله 2:

      {\displaystyle \eta =1-\left({\frac {T_{1}}{T_{2}}}\right)}

      از آنجایی که چرخه اتو از فرآیندهای ایزنتروپیک در طول فشرده سازی (فرآیند 1 تا 2) و انبساط (فرایند 3 تا 4) استفاده می کند، می توان از معادلات ایزنتروپیک گازهای ایده آل و روابط فشار/حجم ثابت برای بدست آوردن معادلات 3 و 4 استفاده کرد. [7]

      معادله 3:

      {\displaystyle \left({\frac {T_{2}}{T_{1}}}\right)=\left({\frac {p_{2}}{p_{1}}}\right)^{ (\گاما -1)/{\گاما }}}

      معادله 4:

      {\displaystyle \left({\frac {T_{2}}{T_{1}}}\right)=\left({\frac {V_{1}}{V_{2}}}\right)^{ (\گاما -1)}}

      جایی که

      {\displaystyle {\gamma }=\left({\frac {C_{\text{p}}}{C_{\text{v}}}}\راست)}

      {\displaystyle {\gamma }}نسبت گرمای ویژه است

      اشتقاق معادلات قبلی به ترتیب با حل این چهار معادله به دست می آید (که در آنآر{\displaystyle R}ثابت گاز خاص است ):

      {\displaystyle C_{\text{p}}\ln \left({\frac {V_{1}}{V_{2}}}\right)-R\ln \left({\frac {p_{2} {p_{1}}}\right)=0}

      {\displaystyle C_{\text{v}}\ln \left({\frac {T_{2}}{T_{1}}}\right)-R\ln \left({\frac {V_{2} {V_{1}}}\right)=0}

      {\displaystyle C_{\text{p}}=\left({\frac {\gamma R}{\gamma -1}}\right)}

      {\displaystyle C_{\text{v}}=\left({\frac {R}{\gamma -1}}\right)}

      ساده کردن بیشتر معادله 4، جایی که{\displaystyle r}نسبت تراکم است{\displaystyle (V_{1}/V_{2})}:

      معادله 5:

      {\displaystyle \left({\frac {T_{2}}{T_{1}}}\right)=\left({\frac {V_{1}}{V_{2}}}\right)^{ (\گاما -1)}=r^{(\گاما -1)}}

      از معکوس کردن معادله 4 و درج آن در معادله 2، بازده حرارتی نهایی را می توان به صورت زیر بیان کرد: [ صفحه مورد نیاز ] [6] [ صفحه مورد نیاز ]

      معادله 6:

      {\displaystyle \eta =1-\left({\frac {1}{r^{(\gamma -1)}}}\right)}

      از تجزیه و تحلیل معادله 6 مشهود است که راندمان چرخه اتو مستقیماً به نسبت تراکم بستگی دارد.{\displaystyle r}. از آنجا که{\displaystyle \gamma }برای هوا 1.4 است، افزایش در{\displaystyle r}افزایش در ایجاد خواهد کرد{\displaystyle \eta }. با این حال{\displaystyle \gamma }برای محصولات احتراق مخلوط سوخت/هوا اغلب تقریباً 1.3 گرفته می شود. بحث فوق حاکی از آن است که داشتن نسبت تراکم بالا کارآمدتر است. نسبت استاندارد برای خودروهای معمولی تقریباً 10:1 است. معمولاً به دلیل امکان خود اشتعال یا " کوبش " که حد بالایی را در نسبت تراکم ایجاد می کند، این مقدار زیاد افزایش نمی یابد. [2] [ صفحه مورد نیاز ] در طول فرآیند فشرده سازی 1-2 دما افزایش می یابد، بنابراین افزایش نسبت تراکم باعث افزایش دما می شود. خود اشتعال زمانی اتفاق می افتد که دمای مخلوط سوخت/هوا قبل از اینکه توسط جلوی شعله مشتعل شود بسیار بالا می رود. ضربه فشرده سازی برای فشرده سازی محصولات قبل از مشتعل شدن مخلوط توسط شعله در نظر گرفته شده است. اگر نسبت تراکم افزایش یابد، مخلوط ممکن است قبل از کامل شدن ضربه فشرده‌سازی، خود به خود مشتعل شود و منجر به "کوبش موتور" شود. این می تواند به اجزای موتور آسیب برساند و اسب بخار ترمز موتور را کاهش دهد.

      قدرت [ ویرایش ]

      توان تولید شده توسط چرخه اتو انرژی تولید شده در واحد زمان است. به موتورهای اتو موتورهای چهار زمانه می گویند. کورس ورودی و کورس تراکمی نیاز به یک چرخش میل لنگ موتور دارد. استروک برق و کورس اگزوز نیاز به چرخش دیگری دارد. برای دو چرخش یک ضربه مولد کار وجود دارد..

      از تجزیه و تحلیل چرخه بالا، کار خالص تولید شده توسط سیستم:

      {\displaystyle \sum {\text{ Work}}=W_{1-2}+W_{3-4}=\left(U_{2}-U_{1}\right)+\left(U_{4} -U_{3}\right)=+4-5=-1}

      (دوباره، با استفاده از قرارداد علامت، علامت منهای به معنای خروج انرژی از سیستم به عنوان کار است)

      اگر واحدهای مورد استفاده MKS بودند، سیکل یک ژول انرژی به شکل کار تولید می کرد. برای یک موتور با جابجایی خاص، مانند یک لیتر، جرم گاز سیستم را می توان با فرض اینکه موتور در دمای استاندارد (20 درجه سانتیگراد) و فشار (1 اتمسفر) کار می کند محاسبه کرد. با استفاده از قانون جهانی گاز، جرم یک لیتر گاز در دمای اتاق و فشار سطح دریا است:

      {\displaystyle M={\frac {PV}{RT}}}

      V = 0.001 m3 ، R = 0.286 kJ/(kg·K)، T = 293 K، P = 101.3 kN/ m2

      M = 0.00121 کیلوگرم

      در دور موتور 3000 دور در دقیقه، 1500 ضربه در دقیقه یا 25 ضربه کار در ثانیه وجود دارد.

      {\displaystyle \sum {\text{ Work}}=1\,{\text{J}}/({\text{kg}}\cdot {\text{stroke}})\times 0.00121\,{\text {kg}}=0.00121\،{\text{J}}/{\text{stroke}}}

      توان 25 برابر بیشتر از آن است زیرا 25 ضربه کار در ثانیه وجود دارد

      {\displaystyle P=25\times 0.00121=0.0303\,{\text{J}}/{\text{s}}\;{\text{یا}}\;{\text{W}}}

      اگر موتور از چند سیلندر با جابه‌جایی یکسان استفاده کند، نتیجه در تعداد سیلندرها ضرب می‌شود. این نتایج حاصل ضرب مقادیر انرژی داخلی است که برای چهار حالت سیستم در پایان هر یک از چهار حرکت (دو چرخش) در نظر گرفته شده است. آنها فقط به خاطر تصویرسازی انتخاب شدند و بدیهی است که ارزش کمی دارند. جایگزینی مقادیر واقعی از یک موتور واقعی، نتایجی نزدیک به موتور ایجاد می کند. نتایج آن‌ها بالاتر از موتور واقعی خواهد بود، زیرا فرضیات ساده‌سازی زیادی در تحلیل وجود دارد که ناکارآمدی‌ها را نادیده می‌گیرند. چنین نتایجی توان خروجی را بیش از حد برآورد می کند.

      افزایش قدرت و کارایی [ ویرایش ]

      تفاوت بین فشار و دما اگزوز و ورودی به این معنی است که با استفاده از یک توربوشارژر می توان مقداری راندمان را افزایش داد، بخشی از انرژی باقی مانده را از جریان اگزوز حذف کرد و آن را به جریان ورودی برای افزایش فشار ورودی انتقال داد. یک توربین گازی می تواند انرژی کار مفیدی را از جریان اگزوز استخراج کند و سپس از آن برای تحت فشار قرار دادن هوای ورودی استفاده شود. فشار و دمای گازهای خروجی با انبساط آنها از طریق توربین گاز کاهش می یابد و سپس این کار به جریان گاز ورودی اعمال می شود و فشار و دمای آن افزایش می یابد. انتقال انرژی باعث بهبود راندمان می شود و چگالی توان موتور نیز بهبود می یابد. هوای ورودی معمولاً به گونه‌ای خنک می‌شود که حجم آن کاهش یابد زیرا کار تولید شده در هر ضربه تابع مستقیم مقدار جرم وارد شده به سیلندر است. هوای متراکم تر در هر چرخه کار بیشتری تولید می کند. عملاً دمای توده هوای ورودی نیز باید کاهش یابد تا از اشتعال زودرس در موتورهای بنزینی جلوگیری شود. از این رو، از یک اینترکولر برای حذف مقداری انرژی به عنوان گرما و در نتیجه کاهش دمای ورودی استفاده می شود. چنین طرحی هم کارایی و هم قدرت موتور را افزایش می دهد.

      استفاده از سوپرشارژر که توسط میل لنگ هدایت می شود، توان خروجی (چگالی توان) را افزایش می دهد، اما راندمان را افزایش نمی دهد، زیرا از بخشی از کار خالص تولید شده توسط موتور برای تحت فشار قرار دادن هوای ورودی استفاده می کند و در غیر این صورت انرژی هدر رفته مرتبط با جریان اگزوز در دمای بالا و فشار به محیط.

      منابع [ ویرایش ]

      1. ^ وو، چی. چرخه های ترمودینامیکی: طراحی و بهینه سازی به کمک کامپیوتر . نیویورک: ام. دکر، 2004. صفحه 99
      2. ^ a b cپرش به بالا: موران، مایکل جی. شاپیرو، هوارد ان. (2006). مبانی ترمودینامیک مهندسی: نسخه SI، واحدهای SI (ویرایش پنجم). چیچستر: وایلی. پ. 376. شابک 978-0-470-03037-0.
      3. ^ مایک بوش. "تکنولوژی 150 ساله". هوانوردی ورزشی : 26.
      4. ↑ گانستون، بیل (1999). توسعه موتورهای پیستونی هوا (ویرایش 2). Sparkford، UK: Patrick Stephens Ltd. p. 21. شابک 978-0-7509-4478-6.
      5. ↑ "چرخه های گرما - الکتروپیدیا" . Woodbank Communications Ltd. بازیابی شده در 2011-04-11 .
      6. ^ پرش به بالا:a b گوپتا، HN مبانی احتراق داخلی . دهلی نو: پرنتیس هال، 2006. چاپ.
      7. ↑ رینولدز و پرکینز (1977). ترمودینامیک مهندسی . مک گراو هیل. ص 249 . شابک 978-0-07-052046-2.

      https://en.wikipedia.org/wiki/Otto_cycle