3-هارمونیک های کروی

توسط علی رضا نقش نیلچی | یکشنبه بیستم اسفند ۱۴۰۲ | 15:46

${\begin{aligned}\mathbf {L} ^{2}Y&=\lambda Y\\L_{z}Y&=mY\end{aligned}}$
$L_{-}L_{+}=\mathbf {L} ^{2}-L_{z}^{2}-L_{z}$ نتیجه می شود که

$0=L_{-}L_{+}^{k}Y=(\lambda -(m+k)^{2}-(m+k))Y.$
بنابراین λ = ( + 1) برای عدد صحیح مثبت = m + k .

موارد فوق همه در نمایش مختصات کروی کار شده است، $\langle \theta ,\varphi |lm\rangle =Y_{l}^{m}(\theta ,\varphi )$ اما ممکن است به صورت انتزاعی تر در پایه کت کروی متعارف کامل بیان شود .
نمایش چند جمله ای هارمونیک [ ویرایش ]
همچنین ببینید: § ابعاد بالاتر
هارمونیک‌های کروی را می‌توان به صورت محدودیت در کره واحد توابع چند جمله‌ای خاص بیان کردآ $\mathbb {R} ^{3}\to \mathbb {C}$ . به طور خاص، ما می گوییم که یک تابع چند جمله ای (با ارزش مختلط).
$p:\mathbb {R} ^{3}\to \mathbb {C}$ درجه همگن است $\ell$ اگر
$p(\lambda \mathbf {x} )=\lambda ^{\ell }p(\mathbf {x} )$
برای همه اعداد حقیقی∈آر $\lambda \in \mathbb {R}$ و همه $x\in \mathbb {R} ^{3}$ . ما این را می گوییم
$p$ هارمونیک است اگر
،
$\Delta p=0,$ جایی کهΔ $\Delta$ لاپلاسی است . سپس برای هر کدام $\ell$ ، تعریف می کنیم
آ={چند جمله ای هارمونیک آ که از نظر درجه همگن هستند }.
$\mathbf {A} _{\ell }=\left\{{\text{چندجمله‌ای هارمونیک }}\mathbb {R} ^{3}\to \mathbb {C} {\text{که همگن هستند درجه }}\ell \right\}.$

مثلاً وقتی=1 $\ell =1$ ، $\mathbf {A} _{1}$ فقط فضای 3 بعدی تمام توابع خطی است $\mathbb {R} ^{3}\to \mathbb {C}$ ، زیرا هر تابعی به طور خودکار هارمونیک است. در ضمن وقتی=2 $\ell =2$ ، ما یک فضای 5 بعدی داریم:
$\mathbf {A} _{2}=\operatorname {span} _{\mathbb {C} }(x_{1}x_{2},\,x_{1}x_{3},\,x_ {2}x_{3},\,x_{1}^{2}-x_{2}^{2},\,x_{1}^{2}-x_{3}^{2}).$

برای هر $\ell$ ، فض
به عنوان مثال، برای هرج $c\in \mathbb {C}$ فرمول
$p(x_{1},x_{2},x_{3})=c(x_{1}+ix_{2})^{\ell }$
یک چند جمله ای همگن درجه را تعریف می کند $\ell$ با دامنه و همدامنه A $\mathbb {R} ^{3}\to \mathbb {C}$ ، که اتفاقا مستقل از $x_{3}$ . این چند جمله ای به راحتی هارمونیک دیده می شود. اگر بنویسیم
$p$ در مختصات کروی $(r,\theta,\varphi)$ و سپس محدود به=1 $r=1$ ، ما بدست می آوریم
پ=جگناه⁡(cos⁡+منگناه⁡)،
$p(\theta,\varphi)=c\sin(\theta)^{\ell }(\cos(\varphi)+i\sin(\varphi))^{\ell },$ که می توان آن را بازنویسی کرد
پ=ج(1-cos2⁡)همن.
$p(\theta ,\varphi )=c\left({\sqrt {1-\cos ^{2}(\theta )}}\right)^{\ell }e^{i\ell \varphi }.$ پس از استفاده از فرمول چند جمله ای لژاندر مرتبط پ $P_{\ell }^{\ell }$ ، ممکن است این را به عنوان فرمول هارمونیک کروی تشخیص دهیم. $Y_{\ell }^{\ell }(\theta,\varphi).$ [7] (به بخش زیر در مورد موارد خاص هارمونیک های کروی مراجعه کنید.)

کنوانسیون ها [ ویرایش ]
متعامد و عادی سازی [ ویرایش ]
صحت حقیقی این بخش مورد مناقشه است . بحث مربوطه را ممکن است در صفحه بحث پیدا کنید . لطفاً کمک کنید تا اطمینان حاصل شود که اظهارات مورد مناقشه به طور قابل اعتماد منبع هستند . ( دسامبر 2017 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )
چندین نرمال سازی مختلف برای توابع هارمونیک کروی لاپلاس رایج است $S^{2}\to \mathbb {C}$ . در سراسر بخش، ما از قرارداد استاندارد استفاده می کنیممتر>0 $m>0$ ( چند جمله ای های مرتبط لژاندر را ببینید )
پ-متر=(-1)متر!(+متر)!
$P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^ {m}$ که نرمال سازی طبیعی با فرمول رودریگز است.

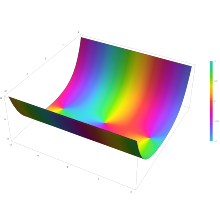
نمودار هارمونیک کروی $Y_{\ell }^{m}(\theta ,\varphi )$ با $\ell =2$ و $m=1$ و= $\varphi =\pi$ در فضای مختلط از $-2-2i$ به $2+2i$ با رنگ های ایجاد شده با تابع Mathematica 13.1 ComplexPlot3D
در آکوستیک ، [8] هارمونیک های کروی لاپلاس به طور کلی به این صورت تعریف می شوند (این قراردادی است که در این مقاله استفاده می شود)

$Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{\frac {(2\ell +1)}{4\pi }}{\frac {(\ell - m)!}{(\ell +m)!}}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }$
در حالی که در مکانیک کوانتومی : [9] [10]

$Y_{\ell }^{m}(\theta ,\varphi )=(-1)^{m}{\sqrt {{\frac {(2\ell +1)}{4\pi }} {\frac {(\ell -m)!}{(\ell +m)!}}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\ ورفی }$

جایی که $P_{\ell }^{m}$ چند جمله ای های لژاندر بدون فاز کاندون-شورتلی (برای جلوگیری از دوبار شمارش فاز) هستند.
در هر دو تعریف، هارمونیک های کروی متعامد هستند

$\int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}\,Y_{\ell '}^ {m'}{}^{*}\,d\Omega =\delta _{\ell \ell '}\,\delta _{mm'}،$
جایی که δ ij دلتای کرونکر است و d Ω = sin( θ ) dφ dθ . این نرمال سازی در مکانیک کوانتومی استفاده می شود زیرا تضمین می کند که احتمال نرمال شده است، به عنوان مثال،

$\int {|Y_{\ell }^{m}|^{2}d\Omega }=1.$

رشته های ژئودزی [11] و تحلیل طیفی استفاده می شود

$Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1)}{\frac {(\ell -m)!}{(\ell + m)!}}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }$

که دارای توان واحد هستند

${\frac {1}{4\pi }}\int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^ {m}\,Y_{\ell '}^{m'}{}^{*}d\Omega =\delta _{\ell \ell '}\,\delta _{mm'}.$

در مقابل، جامعه مغناطیسی [11] از هارمونیک های نیمه نرمال شده اشمیت استفاده می کند

$Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {\frac {(\ell -m)!}{(\ell +m)!}}}\,P_{ \ell }^{m}(\cos {\theta })\,e^{im\varphi }$

که عادی سازی را دارند

$\int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}\,Y_{\ell '}^ {m'}{}^{*}d\Omega ={\frac {4\pi }{(2\ell +1)}}\delta _{\ell \ell '}\,\delta _{mm' }.$

در مکانیک کوانتومی، گاهی اوقات از این نرمال‌سازی نیز استفاده می‌شود و پس از Giulio Racah ، نرمال‌سازی Racah نامیده می‌شود .

می توان نشان داد که همه توابع هارمونیک کروی نرمال شده بالا راضی کننده هستند

${\displaystyle Y_{\ell }^{m}{}^{*}(\theta ,\varphi )=(-1)^{-m}Y_{\ell }^{-m}(\theta ,\ ورفی )$

که در آن بالانویس * نشان دهنده صرف مختلط است. متناوبا، این معادله از رابطه توابع هارمونیک کروی با ماتریس D ویگنر ناشی می شود .

فاز کاندون-شورتلی [ ویرایش ]

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی