3-طرح ریزی سه بعدی

توسط علی رضا نقش نیلچی | جمعه چهاردهم بهمن ۱۴۰۱ | 12:36

طرح ریزی چشم انداز [ ویرایش ]

همچنین ببینید: پرسپکتیو (گرافیکی) ، ماتریس تبدیل ، و ماتریس دوربین

چشم انداز یک جامد هندسی با استفاده از دو نقطه ناپدید شدن. در این حالت، نقشه جامد (برآمدگی متعامد) در زیر پرسپکتیو ترسیم می شود، گویی صفحه زمین را خم می کند.

طرح آکسونومتری طرحی که عناصر مربوطه یک پرسپکتیو صفحه تصویر عمودی را نمایش می دهد. نقطه ایستاده (PS) روی صفحه زمین π قرار دارد و نقطه دید (PV) درست بالای آن قرار دارد. PP نمایش آن بر روی صفحه تصویر α است. LO و LT افق و خطوط زمین هستند ( linea d'orizzonte و linea di terra ). خطوط پررنگ s و q روی π قرار می گیرند و α را به ترتیب در Ts و Tq قطع می کنند. خطوط موازی از طریق PV (قرمز) LO را در نقاط ناپدید Fs و Fq قطع می کنند.: بنابراین می توان برآمدگی های s′ و q′ و همچنین تقاطع R′ آنها را روی R رسم کرد .

طرح ریزی پرسپکتیو یا تبدیل پرسپکتیو یک طرح ریزی خطی است که در آن اجسام سه بعدی بر روی یک صفحه تصویر نمایش داده می شوند. این تأثیری دارد که اجسام دور کوچکتر از اجسام نزدیکتر به نظر می رسند.

همچنین به این معنی است که خطوطی که در طبیعت موازی هستند (یعنی در نقطه بینهایت به هم می رسند) به نظر می رسد در تصویر ارائه شده قطع می شوند. برای مثال، اگر راه‌آهن‌ها با پرسپکتیو تصویر شوند، به نظر می‌رسد که به سمت یک نقطه به نام نقطه ناپدید شدن همگرا می‌شوند . لنزهای عکاسی و چشم انسان به یک شکل عمل می کنند، بنابراین طرح ریزی پرسپکتیو واقعی ترین به نظر می رسد. [5] پرسپکتیو معمولاً به پرسپکتیو یک نقطه‌ای ، دو نقطه‌ای و سه نقطه‌ای تقسیم می‌شود ، بسته به جهت‌گیری صفحه نمایش به سمت محورهای جسم تصویر شده. [6]

روش های طرح ریزی گرافیکی بر دوگانگی بین خطوط و نقاط تکیه دارند، به موجب آن دو خط مستقیم یک نقطه را تعیین می کنند در حالی که دو نقطه یک خط مستقیم را تعیین می کنند. برآمدگی متعامد نقطه چشم بر روی صفحه تصویر، نقطه ناپدید شدن اصلی نامیده می شود (PP در طرح سمت چپ، از اصطلاح ایتالیایی punto principale ، که در دوران رنسانس ابداع شد). [7]

دو نقطه مربوط به یک خط عبارتند از:

تقاطع آن با صفحه تصویر، و
نقطه ناپدید شدن آن، در تقاطع بین خط موازی از نقطه چشم و صفحه تصویر یافت می شود.

نقطه ناپدید شدن اصلی، نقطه ناپدید شدن تمام خطوط افقی عمود بر صفحه تصویر است. نقاط ناپدید شدن همه خطوط افقی روی خط افق قرار دارند. اگر همانطور که اغلب اتفاق می افتد، صفحه تصویر عمودی است، تمام خطوط عمودی به صورت عمودی ترسیم می شوند و نقطه ناپدید شدن محدودی در صفحه تصویر ندارند. روش های گرافیکی مختلفی را می توان به راحتی برای نمایش صحنه های هندسی در نظر گرفت. به عنوان مثال، خطوط ترسیم شده از نقطه چشم در 45 درجه تا صفحه تصویر، دومی را در امتداد دایره ای که شعاع آن فاصله نقطه چشم از صفحه است قطع می کنند، بنابراین ردیابی آن دایره به ساخت تمام نقاط ناپدید 45 درجه کمک می کند. خطوط؛ به طور خاص، تقاطع آن دایره با خط افق از دو نقطه فاصله تشکیل شده است. آنها برای ترسیم کف تخته شطرنج که به نوبه خود برای مکان یابی پایه اشیاء در صحنه مفید هستند. در پرسپکتیو یک جامد هندسی در سمت راست، پس از انتخاب نقطه ناپدید اصلی - که خط افق را تعیین می کند - نقطه ناپدید شدن 45 درجه در سمت چپ نقاشی، توصیف دیدگاه (به همان اندازه دور) را کامل می کند. دو خط از برآمدگی متعامد هر راس، یکی در 45 درجه و دیگری در 90 درجه به صفحه تصویر کشیده شده است. پس از تقاطع خط زمین، آن خطوط به سمت نقطه فاصله (برای 45 درجه) یا نقطه اصلی (برای 90 درجه) می روند. تقاطع جدید آنها نمایانگر نقشه را مشخص می کند. ارتفاعات طبیعی بالای خط زمین اندازه‌گیری می‌شوند و سپس به همان روش پیش‌بینی می‌شوند تا زمانی که به عمودی از روی نقشه برسند.

در حالی که طرح املایی چشم انداز را نادیده می گیرد تا امکان اندازه گیری دقیق را فراهم کند، طرح ریزی پرسپکتیو اجسام دور را کوچکتر نشان می دهد تا واقع گرایی بیشتری ارائه دهد.

فرمول ریاضی [ ویرایش ]

طرح‌ریزی پرسپکتیو در مقایسه با پیش‌بینی‌های املایی نیاز به تعریف درگیرتری دارد. یک کمک مفهومی برای درک مکانیک این طرح این است که تصویر دوبعدی را به گونه‌ای تصور کنید که گویی شیء(ها) از طریق منظره یاب دوربین مشاهده می‌شوند. موقعیت، جهت گیری و میدان دید دوربین ، رفتار تبدیل طرح ریزی را کنترل می کند. متغیرهای زیر برای توصیف این تبدیل تعریف شده اند:

${\mathbf {a}}_{{x,y,z}}$ – موقعیت سه بعدی نقطه A که قرار است پیش بینی شود.
${\mathbf {c}}_{{x,y,z}}$ - موقعیت سه بعدی نقطه C که نشان دهنده دوربین است.
${\mathbf {\theta }}_{{x,y,z}}$ - جهت دوربین (که با زوایای Tait–Bryan نشان داده شده است ).
${\mathbf {e}}_{{x,y,z}}$ - موقعیت سطح نمایشگر نسبت به سوراخ دوربین C. [8]

اکثر قراردادها از مقادیر z مثبت استفاده می کنند (صفحه در جلوی سوراخ سوزن قرار دارد)، با این حال مقادیر z منفی از نظر فیزیکی صحیح تر هستند، اما تصویر هم به صورت افقی و هم به صورت عمودی معکوس می شود. که منجر به:

${\mathbf {b}}_{{x,y}}$ - طرح ریزی دو بعدی ازآ. $\mathbf {a}.$

چه زمانی ، ${\mathbf {c}}_{{x,y,z}}=\langle 0,0,0\rangle ,$ و ${\mathbf {\theta }}_{{x,y,z}}=\langle 0,0,0\rangle ,$ بردار سه بعدی〈1،2،0〉 $\langle 1,2,0\rangle$ به بردار دوبعدی پیش بینی می شود〈1،2〉 $\langle 1,2\rangle$ .

در غیر این صورت، برای محاسبه ${\mathbf {b}}_{{x,y}}$ ابتدا یک بردار را تعریف می کنی ${\mathbf {d}}_{{x,y,z}}$ به عنوان موقعیت نقطه A نسبت به سیستم مختصاتی که توسط دوربین تعریف شده است، با مبدا C و چرخش توسط دوربین $\mathbf {\theta }$ با توجه به سیستم مختصات اولیه این با تفریق حاصل می شود ج $\mathbf {c}$ از جانبآ $\mathbf {a}$ و سپس اعمال چرخش توسط- $-{\mathbf {\theta }}$ به نتیجه این تبدیل اغلب a نامیده می شودتبدیل دوربین ، و می تواند به صورت زیر بیان شود، چرخش را بر حسب چرخش در موردx، yوzمی کند (این محاسبات فرض می کنند که محورها به عنوان یکچپگرد از): [9] [10 ] ]

${\begin{bmatrix}\mathbf {d} _{x}\\\mathbf {d} _{y}\\\mathbf {d} _{z}\end{bmatrix}}={\begin {bmatrix}1&0&0\\0&\cos(\mathbf {\theta } _{x})&\sin(\mathbf {\theta } _{x})\\0&-\sin(\mathbf {\theta } _ {x})&\cos(\mathbf {\theta } _{x})\end{bmatrix}}{\begin{bmatrix}\cos(\mathbf {\theta } _{y})&0&-\sin( \mathbf {\theta } _{y})\\0&1&0\\\sin(\mathbf {\theta } _{y})&0&\cos(\mathbf {\theta } _{y})\end{bmatrix} }{\begin{bmatrix}\cos(\mathbf {\theta } _{z})&\sin(\mathbf {\theta } _{z})&0\\-\sin(\mathbf {\theta } _ {z})&\cos(\mathbf {\theta } _{z})&0\\0&0&1\end{bmatrix}}\left({{\begin{bmatrix}\mathbf {a} _{x}\\ \mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}-{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c } _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}}\right)$

این نمایش مربوط به چرخش با سه زاویه اویلر (به طور صحیح تر، زوایای Tait-Bryan )، با استفاده از قرارداد xyz است که می تواند به صورت "چرخش حول محورهای بیرونی (محورهای صحنه ) به ترتیب z ، y ، x تفسیر شود. (خواندن از راست به چپ)" یا "حول محورهای ذاتی (محورهای دوربین ) به ترتیب x، y، z (خواندن از چپ به راست)". توجه داشته باشید که اگر دوربین نچرخد ${\mathbf {\theta }}_{{x,y,z}}=\langle 0,0,0\rangle$ ، سپس ماتریس ها خارج می شوند (به عنوان هویت)، و این به یک تغییر ساده کاهش می یابد:. ${\mathbf {d}}={\mathbf {a}}-{\mathbf {c}}.$

متناوبا، بدون استفاده از ماتریس (اجازه دهید جایگزین کنیم $a_{x}-c_{x}$ با $\mathbf {x}$ و غیره و به اختصار $\cos \left(\theta _{\alpha }\right)$ به $c_{\alpha }$ و $\sin \left(\theta _{\alpha }\right)$ به $s_{\alpha }$ ): [ توضیح لازم است ]

${\begin{aligned}\mathbf {d} _{x}&=c_{y}(s_{z}\mathbf {y} +c_{z}\mathbf {x} )-s_{y} \mathbf {z} \\\mathbf {d} _{y}&=s_{x}(c_{y}\mathbf {z} +s_{y}(s_{z}\mathbf {y} +c_{ z}\mathbf {x} ))+c_{x}(c_{z}\mathbf {y} -s_{z}\mathbf {x} )\\\mathbf {d} _{z}&=c_{ x}(c_{y}\mathbf {z} +s_{y}(s_{z}\mathbf {y} +c_{z}\mathbf {x} ))-s_{x}(c_{z}\ mathbf {y} -s_{z}\mathbf {x} )\end{تراز شده}}$

سپس این نقطه تبدیل شده را می توان با استفاده از فرمول روی صفحه دوبعدی پیش بینی کرد (در اینجا x / y به عنوان صفحه نمایش استفاده می شود؛ ادبیات همچنین ممکن است از x / z استفاده کند ): [11]

${\begin{aligned}\mathbf {b} _{x}&={\frac {\mathbf {e} _{z}}{\mathbf {d} _{z}}}\mathbf {d } _{x}+\mathbf {e} _{x}،\\[5pt]\mathbf {b} _{y}&={\frac {\mathbf {e} _{z}}{\mathbf { d} _{z}}}\mathbf {d} _{y}+\mathbf {e} _{y}.\end{تراز شده}}$

یا به صورت ماتریسی با استفاده از مختصات همگن ، سیستم

${\begin{bmatrix}\mathbf {f} _{x}\\\mathbf {f} _{y}\\\mathbf {f} _{w}\end{bmatrix}}={\begin {bmatrix}1&0&{\frac {\mathbf {e} _{x}}{\mathbf {e} _{z}}}\\0&1&{\frac {\mathbf {e} _{y}}{\mathbf {e} _{z}}}\\0&0&{\frac {1}{\mathbf {e} _{z}}}\end{bmatrix}}{\begin{bmatrix}\mathbf {d} _{x }\\\mathbf {d} _{y}\\\mathbf {d} _{z}\end{bmatrix}}$

در ارتباط با استدلال با استفاده از مثلث های مشابه، منجر به تقسیم با مختصات همگن می شود و

${\begin{aligned}\mathbf {b} _{x}&=\mathbf {f} _{x}/\mathbf {f} _{w}\\\mathbf {b} _{y} &=\mathbf {f} _{y}/\mathbf {f} _{w}\end{تراز شده}}$

فاصله بیننده از سطح نمایشگر، $\mathbf{e}_z$ ، مستقیماً به میدان دید مربوط می شود که در آن $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ زاویه دید است (توجه: این فرض را بر این می گذارد که نقاط (-1،-1) و (1،1) را در گوشه های سطح دید خود ترسیم کنید)

معادلات فوق را می توان به صورت زیر نیز بازنویسی کرد:

${\begin{aligned}\mathbf {b} _{x}&=(\mathbf {d} _{x}\mathbf {s} _{x})/(\mathbf {d} _{z }\mathbf {r} _{x})\mathbf {r} _{z}،\\\mathbf {b} _{y}&=(\mathbf {d} _{y}\mathbf {s} _ {y})/(\mathbf {d} _{z}\mathbf {r} _{y})\mathbf {r} _{z}.\end{تراز شده}}$

که در آن، ${\mathbf {s}}_{{x,y}}$ اندازه نمایشگر است،، ${\mathbf {r}}_{{x,y}}$ اندازه سطح ضبط ( CCD یا فیلم عکاسی )، ${\mathbf {r}}_{z}$ فاصله سطح ضبط تا مردمک ورودی ( مرکز دوربین )، ${\mathbf {d}}_{z}$ فاصله، از نقطه 3 بعدی در حال نمایش، تا مردمک ورودی است.

عملیات برش و مقیاس بندی بعدی ممکن است برای نگاشت صفحه دوبعدی بر روی هر رسانه نمایشی خاصی ضروری باشد.

پرسپکتیو ضعیف [ ویرایش ]

یک نمایش پرسپکتیو «ضعیف» از همان اصول طرح‌ریزی املایی استفاده می‌کند، اما نیاز به تعیین ضریب مقیاس‌بندی دارد، بنابراین اطمینان حاصل می‌شود که اجسام نزدیک‌تر در طرح‌ریزی بزرگ‌تر به نظر می‌رسند و بالعکس. می توان آن را به عنوان ترکیبی بین یک طرح املایی و یک پرسپکتیو مشاهده کرد و یا به عنوان یک طرح ریزی پرسپکتیو با عمق نقطه منفرد توصیف کرد. $Z_{i}$ با یک عمق ثابت متوسط جایگزین می شود $Z_{\text{ave}}$ ، [12] یا به سادگی به عنوان یک طرح املایی به اضافه یک مقیاس بندی. [13]

بنابراین، مدل با چشم‌انداز ضعیف، در حالی که از یک مدل ساده‌تر، شبیه به چشم‌انداز املایی خالص (غیر مقیاس‌شده) استفاده می‌کند، پیش‌بینی پرسپکتیو را تقریب می‌کند. زمانی که عمق جسم در امتداد خط دید در مقایسه با فاصله از دوربین کم باشد و میدان دید کم باشد، تقریبی منطقی است. با این شرایط می توان فرض کرد که تمام نقاط یک جسم سه بعدی در یک فاصله قرار دارند $Z_{\text{ave}}$ از دوربین بدون خطاهای قابل توجه در طرح ریزی (در مقایسه با مدل پرسپکتیو کامل).

معادله

${\begin{aligned}&P_{x}={\frac {X}{Z_{\text{ave}}}}\\[5pt]&P_{y}={\frac {Y}{Z_{ \text{ave}}}}\end{تراز شده}}$

با فرض فاصله کانونی=1 $f=1$ .

نمودار [ ویرایش ]

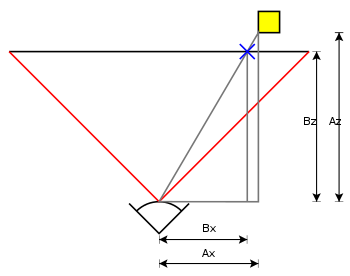
برای تعیین اینکه کدام صفحه x -coordinate مربوط به یک نقطه است $A_{x}، A_{z}$ ضرب مختصات نقطه در:

$B_{x}=A_{x}{\frac {B_{z}}{A_{z}}}$

جایی که

$B_x$ مختصات صفحه نمایش x است

$تبر$ مختصات مدل x است

$B_z$ فاصله کانونی -فاصله محوری از مرکز دوربین تا صفحه تصویر است

$A_z$ فاصله موضوع است.

از آنجایی که دوربین سه بعدی است، همین امر برای مختصات صفحه نمایش y کار می کند و در نمودار و معادله بالا y را جایگزین x می کند.

می‌توانید از آن برای انجام تکنیک‌های برش استفاده کنید، و متغیرها را با مقادیر نقطه‌ای که خارج از زاویه FOV و نقطه داخل Camera Matrix هستند جایگزین کنید.

این تکنیک که با نام «دوربین معکوس» نیز شناخته می‌شود، یک حساب پرسپکتیو پرتاب‌کن با مقادیر شناخته‌شده برای محاسبه آخرین نقطه در زاویه مرئی است که از نقطه نامرئی، پس از اتمام تمام تبدیل‌های مورد نیاز، پرتاب می‌شود.

همچنین ببینید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/3D_projection

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی