تابع دلتا دیراک

تابع دلتا دیراک تابعی است که در سال 1930 توسط PAM دیراک در کتاب اصلی خود در زمینه مکانیک کوانتومی معرفی شد. [1] یک مدل فیزیکی که یک تابع دلتا را به تصویر می‌کشد، توزیع جرمی از جرم کل محدود M - انتگرال بر توزیع جرم است. هنگامی که توزیع کوچکتر و کوچکتر می شود، در حالی که M ثابت است، توزیع جرم به یک جرم نقطه ای منقبض می شود که طبق تعریف وسعت آن صفر است و در عین حال دارای یک انتگرال با ارزش محدود برابر با جرم کل M است. در حد یک جرم نقطه ای توزیع به تابع دلتای دیراک تبدیل می شود.

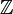
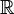
از نظر اکتشافی، تابع دلتای دیراک را می‌توان به‌عنوان بسط دلتای کرونکر از شاخص‌های انتگرال (عناصر ) به شاخص‌های واقعی (عناصر از ) مشاهده کرد. توجه داشته باشید که دلتای کرونکر به عنوان یک "فیلتر" در یک جمع بندی عمل می کند: $\mathbb{Z}$ $\mathbb{R}$

$\sum_{i=m}^n \; f_i\; \delta_{ia} = \begin{cases} f_a & \quad\hbox{if}\quad a\in[m,n] \sub\mathbb{Z} \\ 0 & \quad \hbox{if}\quad a \notin [m,n]. \پایان{موارد}$

در قیاس، تابع دلتای دیراک δ( x - a ) با (جایگزین i با x و جمع بر i با انتگرال روی x ) تعریف می‌شود.

$\int_{a_0}^{a_1} f(x) \delta(xa) \mathrm{d}x = \begin{cases} f(a) & \quad\hbox{if}\quad a\in[a_0، a_1] \sub\mathbb{R}، \\ 0 و \quad \hbox{if}\quad a \notin [a_0,a_1]. \پایان{موارد}$

تابع دلتای دیراک یک نقشه معمولی با رفتار خوب نیست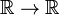 $\mathbb{R} \rightarrow \mathbb{R}$ ، بلکه یک توزیع است که به عنوان یک تابع نامناسب یا تعمیم یافته نیز شناخته می شود . فیزیکدانان ویژگی خاص آن را با بیان اینکه تابع دلتای دیراک تنها به عنوان عاملی در یک انتگرال ("زیر انتگرال") معنا می یابد، بیان می کنند. ریاضیدانان می گویند که تابع دلتا یک تابع خطی در فضایی از توابع آزمایشی است.

فهرست

[ ویرایش ]خواص

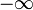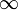معمولاً در تعریف تابع دلتا، کران پایینی و بالایی را به ترتیب برابر با $-\infty$ و $\کوچک$ می گیریم. از اینجا به بعد این کار انجام خواهد شد.

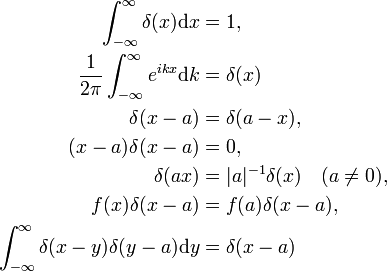
$\begin{align} \int_{-\infty}^{\infty} \delta(x)\mathrm{d}x &= 1, \\ \frac{1}{2\pi}\int_{-\infty }^{\infty} e^{ikx} \mathrm{d}k &= \delta(x) \\ \delta(xa) &= \delta(ax), \\ (xa)\delta(xa) & = 0، \\ \delta(ax) &= |a|^{-1} \delta(x) \quad (a \ne 0)، \\ f(x) \delta(xa) &= f(a ) \delta(xa), \\ \int_{-\infty}^{\infty} \delta(xy)\delta(ya)\mathrm{d}y &= \delta(xa) \end{align}$

اثبات این خصوصیات توسط فیزیکدان با ایجاد جانشینی مناسب در انتگرال و استفاده از قوانین معمولی حساب انتگرال انجام می شود. تابع دلتا به عنوان تبدیل فوریه تابع واحد f ( x ) = 1 (ویژگی دوم) در زیر ثابت خواهد شد. آخرین ویژگی قیاس ضرب دو ماتریس هویت است .

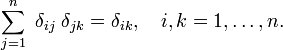
$\sum_{j=1}^n \;\delta_{ij}\;\delta_{jk} = \delta_{ik}, \quad i,k=1,\ldots, n.$

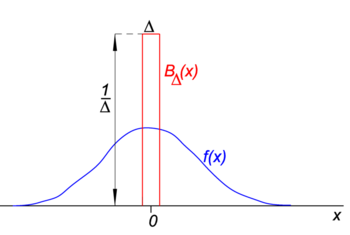
شکل 1. تابع بلوک ("boxcar") (قرمز) ضرب در تابع منظم f ( x ) (آبی).

[ ویرایش ]دنباله های همگرا دلتا

خانواده هایی از توابع منظم F α ( x ) وجود دارد که اعضای خانواده با مقدار یک پارامتر واحد تفاوت دارند. نمونه ای از چنین خانواده ای توسط خانواده توابع گاوسی F α ( x ) = exp(-α x² ) تشکیل شده است، که در آن مقادیر مختلف پارامتر واحد α اعضای مختلف را متمایز می کند. وقتی همه اعضا به صورت خطی نرمال پذیر باشند، یعنی انتگرال زیر بدون توجه به α محدود است،

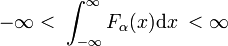
$-\infty < \; \int_{-\infty}^{\infty} F_\alpha(x) \mathrm{d}x \; < \infty$

و همه اعضا در حدود x = 0 به اوج می رسند ، سپس خانواده ممکن است یک دنباله همگرا دلتا را تشکیل دهند .

[ ویرایش ]توابع بلوک کردن

ساده ترین مثال از یک دنباله همگرا دلتا توسط خانواده توابع بلوک تشکیل شده است که با Δ مثبت مشخص می شود.

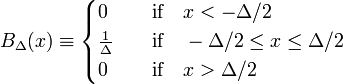
$B_\Delta(x)\equiv \begin{cases} 0 &\quad\hbox{if}\quad x< -\Delta/2 \\ \frac{1}{\Delta} &\quad\hbox{if} \quad -\Delta/2 \le x\le \Delta/2 \\ 0 &\quad\hbox{if}\quad x> \Delta/2 \\ \end{موارد}$

در شکل 1 تابع بلوک B Δ به رنگ قرمز نشان داده شده است. واضح است که مساحت (عرض ضربدر ارتفاع) زیر منحنی قرمز بدون توجه به مقدار Δ برابر است با واحد،

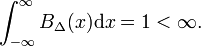
$\int_{-\infty}^{\infty} B_\Delta(x) \mathrm{d}x = 1 < \infty.$

اجازه دهید تابع دلخواه f ( x ) (آبی در شکل 1) پیوسته (بدون جهش) و محدود در همسایگی x = 0 باشد. وقتی Δ بسیار کوچک می شود و تابع بلوک بسیار باریک (و لزوماً بسیار زیاد است زیرا عرض ضربدر ارتفاع ثابت است) حاصل ضرب f ( x ) B Δ ( x ) تقریباً برابر با f (0) B Δ ( x ) می شود. . هرچه بلوک باریکتر باشد تقریب بهتری خواهد داشت. بنابراین برای Δ به صفر می‌رسد،

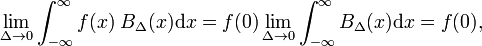
$\lim_{\Delta\rightarrow0} \int_{-\infty}^{\infty} f(x)\;B_\Delta(x) \mathrm{d}x = f(0)\lim_{\Delta\rightarrow0 } \int_{-\infty}^{\infty} B_\Delta(x) \mathrm{d}x = f(0)،$

که ممکن است با تعریف تابع دلتا مقایسه شود،

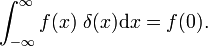
$\int_{-\infty}^{\infty} f(x)\;\delta(x) \mathrm{d}x = f(0) .$

این نشان می دهد که خانواده توابع بلوک برای کاهش پارامتر Δ به تابع دلتای دیراک همگرا می شوند. خانواده یک دنباله همگرا دلتا را تشکیل می دهد :

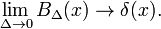
$\lim_{\Delta \rightarrow 0}B_\Delta(x) \rightarrow \delta(x).$

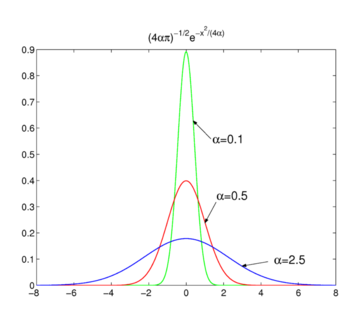
شکل 2. توابع گاوسی.

توجه : ما در کل محور واقعی یکپارچه شدیم. بدیهی است که این ضروری نیست، ما می‌توانستیم بال‌های صفر تابع بلوک را کنار بگذاریم و فقط روی قوز در وسط، از -Δ/2 تا +Δ/2 ادغام کنیم. در متون ریاضی، به عنوان مثال Ref. [2] ، این اصلاح در حدود ادغام در تعریف دنباله همگرا دلتا گنجانده شده است. یعنی لازم است که انتگرال های روی دو بال در حد ناپدید شوند. از آنجایی که توالی‌های همگرای دلتا که در کاربردهای فیزیکی با آن مواجه می‌شوند، معمولاً این شرایط را برآورده می‌کنند، ما تعریف دقیق‌تر ریاضی را حذف می‌کنیم.

[ ویرایش ]توابع گاوسی

خانواده را در نظر بگیرید،

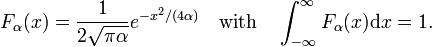
$F_\alpha(x) = \frac{1}{2\sqrt{\pi\alpha}} e^{-x^2/(4\alpha)}\quad\hbox{with}\quad \int_{- \infty}^\infty F_\alpha(x)\mathrm{d} x = 1.$

همانطور که در شکل 2 نشان داده شده است، توابع در حدود x = 0 اوج می گیرند و برای کاهش α باریکتر می شوند. از این رو خانواده توابع گاوسی یک دنباله همگرای دلتا را تشکیل می دهند.

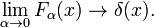
$\lim_{\alpha \rightarrow 0} F_\alpha (x) \rightarrow \delta(x).$

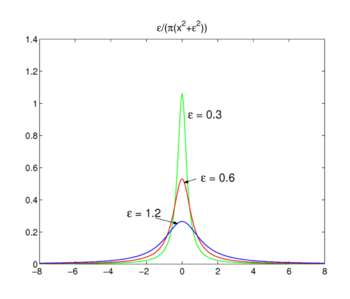
شکل 3. توابع لورنتس-کوشی

[ ویرایش ]توابع لورنتس-کوشی

خانواده توابع نشان داده شده در شکل 3

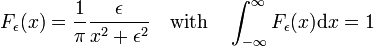
$F_\epsilon(x) = \frac{1}{\pi}\frac{\epsilon}{x^2+\epsilon^2}\quad\hbox{with}\quad \int_{-\infty}^{ \infty} F_\epsilon(x)\mathrm{d}x = 1$

یک دنباله دلتا همگرا تشکیل می دهد،

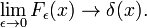
$\lim_{\epsilon \rightarrow 0} F_\epsilon(x) \rightarrow \delta(x).$

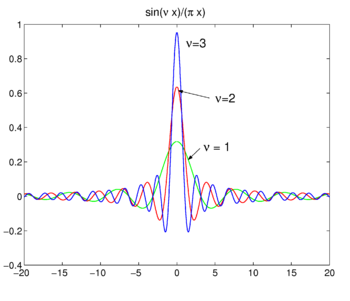
شکل 4. توابع سینک.

[ ویرایش ]توابع سینک

خانواده توابع (که اغلب توابع sinc نامیده می شوند) نشان داده شده در شکل 4 هستند

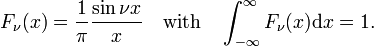
$F_\nu(x) = \frac{1}{\pi} \frac{\sin\nu x}{x}\quad\hbox{with}\quad \int_{-\infty}^{\infty} F_ \nu(x)\mathrm{d}x = 1.$

این خانواده برای افزایش ν به تابع دلتا همگرا می شود

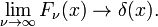
$\lim_{\nu \rightarrow \infty} F_\nu(x) \rightarrow \delta(x).$

این حد به راحتی به نمایش انتگرال فوریه تابع دلتا منتهی می شود:

$\int^\nu_{-\nu} e^{ikx} \mathrm{d}k = \frac{1}{ix} \left[ e^{ikx} \right]_{-\nu}^{\ nu} = \frac{2\sin \nu x}{x}،$

به طوری که

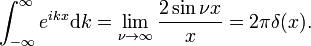
$\int^\infty_{-\infty} e^{ikx} \mathrm{d}k = \lim_{\nu \rightarrow \infty } \frac{2\sin \nu x}{x} = 2\pi\ دلتا (x).$

تابع دلتای دیراک تبدیل فوریه تابع واحد f ( x ) = 1 است.

[ ویرایش ]مشتقات تابع دلتا

یک تابع متمایز f ( x ) را در نظر بگیرید که در بی نهایت به اضافه و منهای ناپدید می شود. ادغام با قطعات

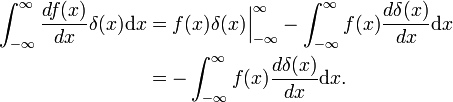
$\begin{align} \int_{-\infty}^{\infty} \frac{df(x)}{dx} \delta(x) \mathrm{d}x &= f(x)\delta(x) \Big|_{-\infty}^{\infty} - \int_{-\infty}^{\infty} f(x) \frac{d \delta(x)}{dx} \mathrm{d}x \\ &= - \int_{-\infty}^{\infty} f(x) \frac{d \delta(x)}{dx} \mathrm{d}x. \پایان{تراز}$

همانطور که قانون گردش و هرمیتیسیته عملگر تکانه مکانیکی کوانتومی را اثبات می 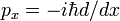$p_x = -i\hbar d/dx$ کنیم، در اینجا نشان دادیم که d/d x ضد هرمیت است.

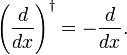
$\left(\frac{d}{dx}\right)^\dagger = - \frac{d}{dx}.$

در واقع، وقتی انتگرال را به عنوان یک محصول درونی می نویسیم ، از یکپارچگی جزئی و ناپدید شدن f ( x ) در حدود انتگرال نتیجه می شود که

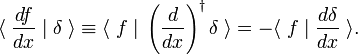
$\langle\; \frac{df}{dx}\; |\; \delta \;\rangle \equiv \langle\; f\;|\; \left(\frac{d}{dx}\right)^\dagger \delta \; \rangle = - \langle\; f\;|\; \frac{d\delta}{dx} \; \رنگ .$

این قانون گردش به عنوان تعریف مشتق تابع دلتا استفاده می شود.

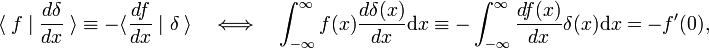
$\langle\; f\;|\; \frac{d\delta}{dx} \; \rangle \equiv - \langle \frac{df}{dx}\; |\; \delta \;\rangle \quad\Longleftrightarrow\quad \int_{-\infty}^{\infty} f(x) \frac{d \delta(x)}{dx} \mathrm{d}x \equiv - \int_{-\infty}^{\infty} \frac{df(x)}{dx} \delta(x) \mathrm{d}x = - f'(0)،$

که در آن عدد اول اولین مشتق f (x) را نشان می دهد. با توجه به تعریف تابع دلتا، اولین مشتق با x = 0 ارزیابی می شود. با استفاده از m ضربدر قانون گردش، نتیجه می شود که m مشتق تابع دلتا با تعریف می شود.

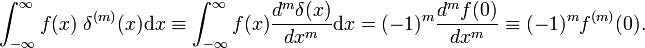
$\int_{-\infty}^{\infty} f(x)\; \delta^{(m)}(x) \mathrm{d}x \equiv \int_{-\infty}^{\infty} f(x) \frac{d^m \delta(x)}{dx^ m} \mathrm{d}x = (-1)^m \frac{d^mf(0)}{dx^m} \equiv (-1)^mf^{(m)}(0).$

[ ویرایش ]خواص مشتق

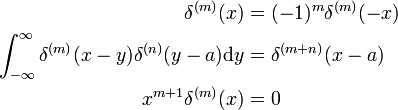
$\begin{align} \delta^{(m)}(x) &= (-1)^m \delta^{(m)}(-x)\\ \int_{-\infty}^\infty \delta ^{(m)}(xy)\delta^{(n)}(ya)\mathrm{d}y &= \delta^{(m+n)}(xa) \\ x^{m+1} \delta^{(m)}(x)&= 0\\ \end{تراز کردن}$

این نتایج را می توان با جایگزینی x → − x و استفاده از قانون گردش برای d/d x اثبات کرد (به بالا مراجعه کنید).

[ ویرایش ]اولیه

همانطور که در اینجا نشان داده شده است ، ابتدایی (همچنین به عنوان ضد مشتق، یا انتگرال نامشخص شناخته می شود) دلتای دیراک، تابع گام Heaviside H ( x ) است.

$H'(x) \equiv \frac{d H(x)}{dx} = \delta(x).$

به وضوح،

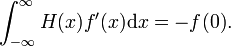
$\int_{-\infty}^{\infty} H(x) f'(x) \mathrm{d}x = -f(0).$

[ ویرایش ]تابع دلتای دیراک در سه بعدی

تابع دلتا را در فضای سه بعدی به صورت δ( r ) بنویسید، با r = ( x ، y ، z )، و تعریف کنید،

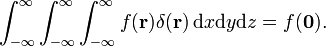
$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\mathbf{r})\delta(\mathbf{ r})\، \mathrm{d}x \mathrm{d}y\mathrm{d}z = f(\mathbf{0}).$

که از آن به طور کلی تر می آید،

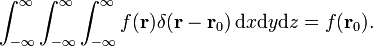
$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\mathbf{r} )\delta(\mathbf{ r}-\mathbf{r}_0)\، \mathrm{d}x \mathrm{d}y\mathrm{d}z = f(\mathbf{r}_0).$

تابع دلتای سه بعدی را می توان فاکتور گرفت

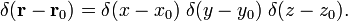
$\delta(\mathbf{r}-\mathbf{r}_0) = \delta(x-x_0)\; \delta(y-y_0)\;\delta(z-z_0).$

در مختصات قطبی کروی

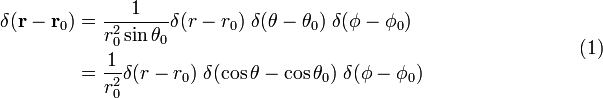
$\begin{align} \delta(\mathbf{r}-\mathbf{r}_0) &= \frac{1}{r_0^2\sin\theta_0} \delta(r-r_0)\; \delta(\theta-\theta_0)\;\delta(\phi-\phi_0) \\ &= \frac{1}{r_0^2} \delta(r-r_0)\; \delta(\cos\theta-\cos\theta_0)\;\delta(\phi-\phi_0) \\ \end{align} \qquad\qquad\qquad\qquad (1)$

اثبات معادله (1)

نوشتن

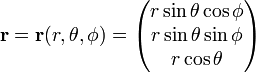
$\mathbf{r} = \mathbf{r}(r,\theta, \phi) = \begin{pmatrix} r\sin\theta\cos\phi \\ r\sin\theta\sin\phi \\ r\ cos\theta \\ \end{pmatrix}$

ژاکوبین ( جذاب ژاکوبی) این تبدیل از مختصات دکارتی به مختصات قطبی کروی است.

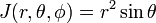
$J(r,\theta,\phi) = r^2\sin\theta \,$

در نظر گرفتن

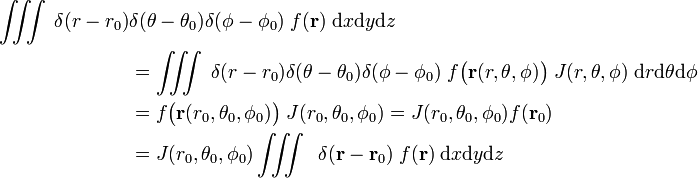
$\begin{alignat}{2} \iiint\; \delta(r-r_0)&\delta(\theta-\theta_0)\delta(\phi-\phi_0)\;f(\mathbf{r})\; \mathrm{d}x \mathrm{d}y\mathrm{d}z \\ &= \iiint\; \delta(r-r_0)\delta(\theta-\theta_0)\delta(\phi-\phi_0)\;f\big(\mathbf{r}(r,\theta,\phi)\big)\; J(r,\theta,\phi)\;\mathrm{d}r \mathrm{d}\theta\mathrm{d}\phi \\ &= f\big(\mathbf{r}(r_0,\theta_0 ,\phi_0)\big)\; J(r_0،\theta_0،\phi_0) = J(r_0،\theta_0،\phi_0) f(\mathbf{r}_0)\\ &= J(r_0،\theta_0،\phi_0) \iiint\; \;\delta(\mathbf{r}-\mathbf{r}_0)\;f(\mathbf{r})\; \mathrm{d}x \mathrm{d}y\mathrm{d}z \end{alignat}$

به طوری که

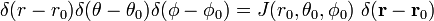
$\delta(r-r_0)\delta(\theta-\theta_0)\delta(\phi-\phi_0) = J(r_0،\theta_0،\phi_0)\; \delta(\mathbf{r}-\mathbf{r}_0)\,$

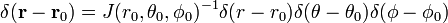
$\delta(\mathbf{r}-\mathbf{r}_0) = J(r_0,\theta_0,\phi_0)^{-1} \delta(r-r_0)\delta(\theta-\theta_0)\delta (\phi-\phi_0) \,$

آخرین خط در معادله (1) از قانون زنجیره پیروی می کند.

ویژگی مفید و پرکاربرد زیر در اینجا ثابت شده است .

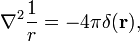
$\nabla^2\frac{1}{r} = - 4\pi \delta(\mathbf{r})،$

که در آن ∇ 2 عملگر لاپلاس در مختصات دکارتی سه بعدی و r طول r است.

منبع

https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/wiki/Dirac_delta_function.html

+ نوشته شده در جمعه بیست و سوم اردیبهشت ۱۴۰۱ ساعت 13:45 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی