از ویکیپدیا، دانشنامه آزاد

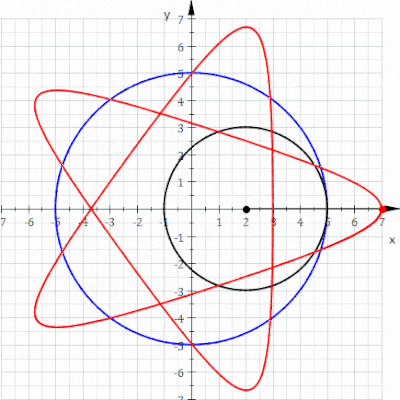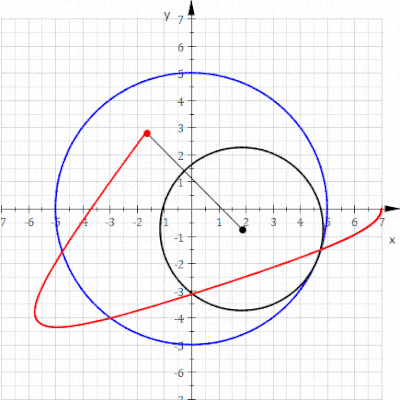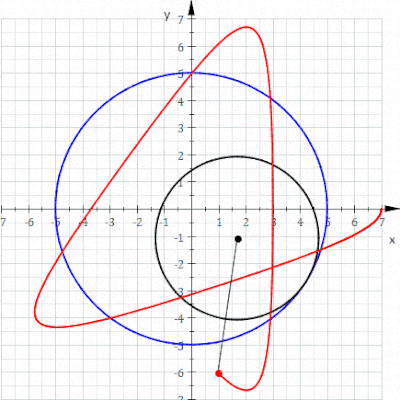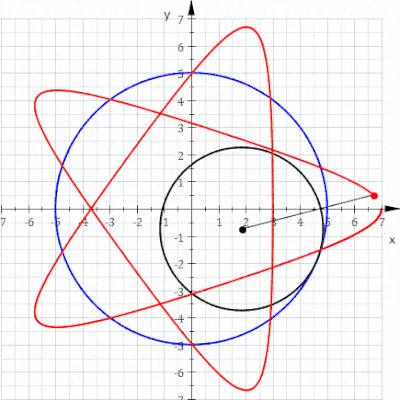
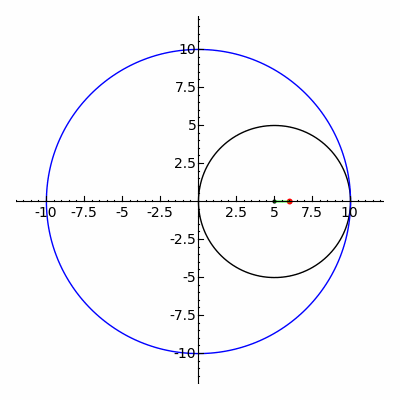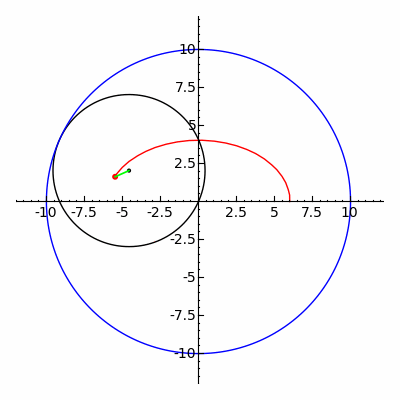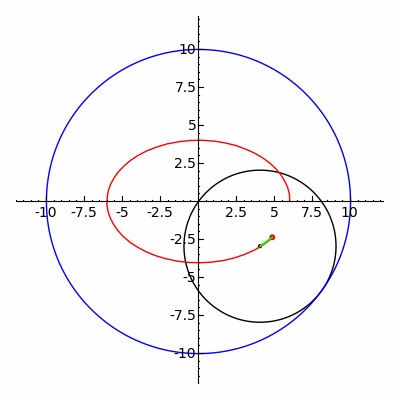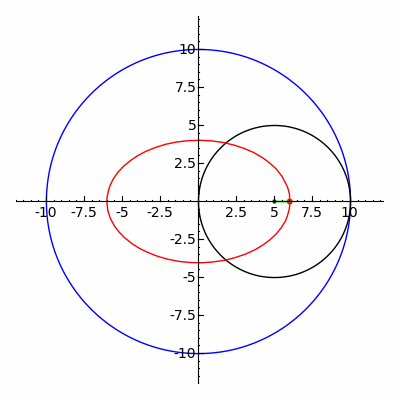
          منحنی قرمز یک هیپوتروکوئید است که زمانی که دایره سیاه کوچکتر در داخل دایره آبی بزرگتر می چرخد ​​ترسیم می شود (پارامترها R = 5، r = 3، d = 5 هستند ).

          در هندسه ، هیپوتروکوئید رولتی است که توسط نقطه ای متصل به دایره ای با شعاع r که به دور داخل یک دایره ثابت با شعاع R می چرخد، ردیابی می شود ، جایی که نقطه فاصله ای d از مرکز دایره داخلی است.

          معادلات پارامتریک هیپوتروکوئید عبارتند از: [1]

          {\displaystyle {\begin{aligned}&x(\theta )=(Rr)\cos \theta +d\cos \left({Rr \over r}\theta \right)\\&y(\theta )=(Rr )\sin \theta -d\sin \left({Rr \over r}\theta \right)\end{تراز شده}}}

          که در آن θ زاویه تشکیل شده توسط افقی و مرکز دایره غلتشی است (اینها معادلات قطبی نیستند زیرا θ زاویه قطبی نیست). هنگامی که در رادیان اندازه گیری می شود، θ مقادیری از 0 تا را می گیرد{\displaystyle 2\pi \times {\tfrac {\operatorname {LCM} (r,R)}{R}}}(که در آن LCM کمترین مضرب مشترک است ).

          موارد خاص شامل هیپوسایکلوئید با d = r و بیضی با R = 2 r و d ≠ r است . [2] خروج از مرکز بیضی است

          {\displaystyle e={\frac {2{\sqrt {d/r}}}{1+(d/r)}}}

          تبدیل شدن به 1 وقتی {\displaystyle d=r}(نگاه کنید به زوج طوسی ).

          بیضی (به رنگ قرمز کشیده شده) ممکن است به عنوان یک مورد خاص از هیپوتروکوئید، با R = 2 r ( زوج طوسی ) بیان شود. در اینجا R = 10، r = 5، d = 1 .

          اسباب بازی کلاسیک اسپیروگراف منحنی های هیپوتروکوئید و اپی تروکوئید را مشخص می کند .

          هیپوتروکوئیدها پشتیبانی از مقادیر ویژه برخی از ماتریس های تصادفی را با همبستگی چرخه ای توصیف می کنند. [3]

          همچنین ببینید [ ویرایش ]

          منابع [ ویرایش ]

          1. ↑ جی. دنیس لارنس (1972). کاتالوگ منحنی های صفحه ویژه . انتشارات دوور. صص 165-168 . شابک 0-486-60288-5.
          2. ↑ گری، آلفرد (29 دسامبر 1997). هندسه دیفرانسیل مدرن منحنی ها و سطوح با ریاضیات (ویرایش دوم). مطبوعات CRC. پ. 906. شابک 9780849371646.
          3. ^ آسیتونو، پاو ویلیملیس؛ راجرز، تیم؛ شومروس، هنینگ (16-07-2019). "قانون هیپوتروکوئیدی جهانی برای ماتریس های تصادفی با همبستگی چرخه ای" . بررسی فیزیکی E. 100 (1): 010302. arXiv : 1812.07055 . Bibcode : 2019PhRvE.100a0302A . doi : 10.1103/PhysRevE.100.010302 . PMID 31499759 . S2CID 119325369 .

          https://en.wikipedia.org/wiki/Hypotrochoid