از ویکیپدیا، دانشنامه آزاد

این مقاله در مورد گراف 3 منظم است. برای گراف مرتبط با یک گروه کوکستر، گراف کوکستر را ببینید .

نباید با گراف توت-کوکستر اشتباه گرفته شود .

گراف کاکستر

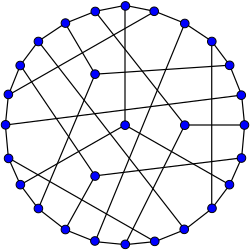
گراف کوکستر

به نامHSM کوکستر

رگه ها28

لبه ها42

شعاع4

قطر4

بند7

اتومورفیسم ها336 ( PGL 2 (7))

عدد کروماتیک3

شاخص رنگی3

ضخامت کتاب3

شماره صف2

خواصفاصله متقارن
-
فاصله منظم-مکعب
هیپوهامیلتونین
متعدی

جدول گرافها و پارامترها

در زمینه ریاضی نظریه گراف ، گراف کاکستر یک گراف 3 منظم با 28 راس و 42 یال است. [1] این یکی از 13 گراف منتظم فاصله مکعبی شناخته شده است . [2] این نام از هارولد اسکات مک دونالد کاکستر گرفته شده است .

خواص [ ویرایش ]

گراف کوکستر دارای عدد کروماتیک 3، شاخص رنگی 3، شعاع 4، قطر 4 و دور 7 است. همچنین یک گراف 3-متصل به رأس و یک گراف متصل به لبه است . دارای ضخامت کتاب 3 و صف شماره 2 است . [3]

گراف کاکستر هیپوهامیلتونی است : خود چرخه همیلتونی ندارد اما هر گرافی که با حذف یک رأس از آن شکل می‌گیرد، همیلتونی است. دارای شماره تقاطع مستطیلی 11 است و کوچکترین گراف مکعبی با آن عدد تلاقی [4] است (توالی A110507 در OEIS ).

ساخت و ساز [ ویرایش ]

ساده ترین ساخت گراف کاکستر از هواپیمای فانو است . 7 C 3 = 35 3 ترکیب ممکن روی 7 شی را در نظر بگیرید . 7 سه قلو که مطابق با خطوط هواپیمای فانو هستند را دور بیندازید و 28 سه قلو باقی بمانید. اگر دو سه قلو ناهمگون هستند پیوند دهید. نتیجه گراف کوکستر است. ( تصویر را ببینید .) این ساختار گراف کوکستر را به عنوان یک زیرگراف القایی از گراف فرد O 4 نشان می دهد که به عنوان گراف Kneser KG 7,3 نیز شناخته می شود .

گراف کوکستر همچنین ممکن است از گراف هیوود منتظم با فاصله کوچکتر با ساخت یک راس برای هر 6 چرخه در گراف هیوود و یک یال برای هر جفت مجزا از 6 چرخه ساخته شود. [5]

گراف کوکستر ممکن است از گراف هافمن-سینگلتون مشتق شده باشد . هر رأس v را در گراف هافمن-سینگلتون در نظر بگیرید. یک مجموعه مستقل از سایز 15 وجود دارد که شامل v . 7 همسایه v و کل مجموعه مستقل از جمله v را حذف کنید و گراف کوکستر را پشت سر بگذارید.

ویژگی های جبری [ ویرایش ]

گروه اتومورفیسم گراف کاکستر یک گروه از مرتبه 336 است . بنابراین، گراف کوکستر یک گراف متقارن است . دارای اتومورفیسم هایی است که هر راس را به هر راس دیگری و هر یال را به هر یال دیگری می برد. طبق سرشماری فاستر ، گراف کاکستر که به عنوان F28A ارجاع داده شده است، تنها گراف متقارن مکعبی در 28 راس است. [7]

گراف کوکستر نیز به طور منحصر به فرد توسط طیف گراف آن ، مجموعه مقادیر ویژه گراف ماتریس مجاورت آن تعیین می شود . [8]

به عنوان یک گراف راس گذرا متصل محدود که شامل چرخه همیلتونی نیست ، گراف کاکستر نمونه ای متضاد برای گونه ای از حدس لوواس است ، اما فرمول متعارف حدس یک مسیر همیلتونی را می خواهد و توسط گراف کاکستر تأیید می شود.

تنها پنج نمونه از گراف رأس گذرا بدون چرخه هامیلتونی شناخته شده است: گراف کامل K2 ، گراف پترسن ، گراف کاکستر و دو گراف مشتق شده از گرافهای پترسن و کاکستر با جایگزینی هر راس با یک مثلث . [9]

چند جمله ای مشخصه گراف کاکستر است(x-3)(x-2)^{8}(x+1)^{7}(x^{2}+2x-1)^{6}. این تنها گراف با این چند جمله ای مشخص است که آن را به گرافی تبدیل می کند که توسط طیف آن تعیین می شود.

گالری [ ویرایش ]

طرح بندی [ ویرایش ]

اینها نمایش های متفاوتی از گراف کوکستر با استفاده از برچسب های رأس یکسان هستند. چهار رنگ و هفت رأس هر رنگ وجود دارد.
هر رأس قرمز، سبز یا آبی با دو راس همرنگ (لبه های نازک 7 چرخه) و یک راس سفید (لبه های ضخیم) متصل است.

هفت ضلعی قرمز ، هپتاگرام حاد سبز و آبی
سمت چپ: تقارن چرخشی 7 برابر

در 24 گون
تقارن چرخشی 3 برابر

تقارن دو وجهی 3 برابری
( نوعی را با رئوس صفحه فانو مقایسه کنید )

در تقارن آینه هشت ضلعی

خواص [ ویرایش ]

گراف به دست آمده توسط هر برش لبه از کوکستر به همیلتون متصل است.

عدد رنگی گراف کاکستر 3 است.

عدد متقاطع مستطیلی گراف کوکستر 11 است.

منابع [ ویرایش ]

  1. ↑ وایستاین، اریک دبلیو. "کوکستر Graph" . دنیای ریاضی .
  2. ^ بروور، AE; کوهن، AM; و Neumaier، A. گرافهای فاصله-منظم. نیویورک: Springer-Verlag، 1989.
  3. ^ ولز، جسیکا؛ مهندسی طرح های خطی با SAT. پایان نامه کارشناسی ارشد، دانشگاه توبینگن، 2018
  4. ^ هایتورپ، مایکل؛ نیوکمب، الکس (2018)، هیچ گراف مکعبی روی 26 رأس با شماره 11 وجود ندارد ، arXiv : 1804.10336
  5. ↑ Dejter، Italo J. (2011) ، "From the کوکستر graph to the Klein graph"، Journal of Graph Theory ، 70 : 1–9، arXiv : 1002.1960 ، doi : 10.1002/jgt.20597 ، S44ID81 . .
  6. ^ داده های Royle, G. F028A [ پیوند مرده دائمی ]
  7. ↑ Conder, M. and Dobcsányi, P. "گرافهای متقارن سه ظرفیتی تا ۷۶۸ راس." جی. ترکیب. ریاضی. ترکیب کنید. محاسبه کنید. 40، 41-63، 2002.
  8. ↑ ER van Dam و WH Haemers، خصوصیات طیفی برخی از گرافهای منظم فاصله. ج. ترکیب جبری. 15، صفحات 189-202، 2003
  9. ↑ رویل، جی. "گرافهای متقارن مکعبی (سرشماری فاستر)." بایگانی شده در 12-09-2015 در ماشین Wayback
  • کوکستر، HSM "گراف i." Proc. ریاضی لندن. Soc. 46، 117-136، 1983.

https://en.wikipedia.org/wiki/Coxeter_graph