از ویکی پدیا، دانشنامه آزاد

نمودار هیوود
به نام	پرسی جان هیوود
رگه ها	14
لبه ها	21
شعاع	3
قطر	3
بند	6
اتومورفیسم ها	336 ( PGL 2 (7) )
عدد کروماتیک	2
شاخص رنگی	3
جنس	1
ضخامت کتاب	3
شماره صف	2
خواص	قفس مکعبی دو قسمتی فاصله-گذرا فاصله-منظم حلقوی همیلتونی متقارن شرقی ساده
جدول نمودارها و پارامترها

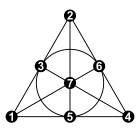
در زمینه ریاضی نظریه گراف ، گراف هیوود یک گراف بدون جهت با 14 راس و 21 یال است که به نام پرسی جان هیوود نامگذاری شده است . [1]

خواص ترکیبی [ ویرایش ]

نمودار مکعبی است و تمام چرخه های نمودار دارای شش یا بیشتر یال هستند. هر نمودار مکعبی کوچک‌تر چرخه‌های کوتاه‌تری دارد، بنابراین این نمودار قفس 6 ، کوچک‌ترین نمودار مکعبی دور 6 است. این یک نمودار گذرای فاصله است (به سرشماری فاستر مراجعه کنید ) و بنابراین فاصله منظم است . [2]

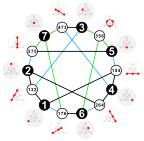
24 تطابق کامل در نمودار هیوود وجود دارد . برای هر تطابق، مجموعه یال‌هایی که مطابقت ندارند، یک چرخه همیلتونی را تشکیل می‌دهند . به عنوان مثال، شکل، رئوس نمودار را نشان می دهد که روی یک چرخه قرار گرفته است، با قطرهای داخلی چرخه که یک تطابق را تشکیل می دهند. با تقسیم لبه‌های چرخه به دو تطابق، می‌توانیم نمودار هیوود را به سه تطابق کامل (یعنی 3 رنگ کردن لبه‌های آن ) به هشت روش مختلف تقسیم کنیم. [2] هر دو تطابق کامل، و هر دو چرخه همیلتونی، می‌توانند توسط یک تقارن نمودار به یکدیگر تبدیل شوند. [3]

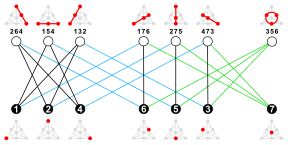
28 چرخه شش رأسی در نمودار هیوود وجود دارد. هر 6 چرخه دقیقاً از سه 6 چرخه دیگر جدا است. در بین این سه 6 چرخه، هر یک تفاوت متقارن دو چرخه دیگر است. نمودار با یک گره در هر 6 چرخه، و یک یال برای هر جفت مجزا از 6 چرخه، نمودار Coxeter است . [4]

خواص هندسی و توپولوژیکی [ ویرایش ]

نمودار هیوود یک گراف حلقوی است . یعنی می توان آن را بدون عبور از روی چنبره جاسازی کرد . یک تعبیه از این نوع، رئوس و لبه های خود را در فضای اقلیدسی سه بعدی به عنوان مجموعه رئوس و لبه های یک چندوجهی غیر محدب با توپولوژی یک چنبره، چند وجهی Szilassi قرار می دهد . تعبیه دیگر موارد زیر است: هواپیما را با استفاده از شش ضلعی معمولی کاشی کنید و آنها را به صورت دوره ای با 7 رنگ رنگ کنید. برای هر رنگی، شش ضلعی های این رنگ یک شبکه مثلثی تشکیل می دهند. در این شبکه می توان متوازی الاضلاع را با مرکز در وسط شش ضلعی های رنگ انتخابی گرفت. با تا کردن این متوازی الاضلاع، با استفاده از نمودار هیوود (مانند تصویر در گالری زیر، اما با مربع) یک چنبره با 7 شش ضلعی کاشی‌کاری شده است.

این نمودار از نام پرسی جان هیوود نامگذاری شده است که در سال 1890 ثابت کرد که در هر تقسیم بندی چنبره به چند ضلعی، مناطق چند ضلعی را می توان حداکثر با هفت رنگ رنگ آمیزی کرد. [5] [6] نمودار هیوود یک بخش فرعی از چنبره را با هفت ناحیه مجاور متقابل تشکیل می‌دهد که نشان می‌دهد این کران تنگ است.

صفحه فانو و دو نمایش گراف لوی آن (در زیر به عنوان یک گراف دو بخشی )

گراف هیوود، نمودار لوی صفحه فانو است ، نموداری که نمایانگر انقباضات بین نقاط و خطوط در آن هندسه است. با این تفسیر، 6 چرخه در نمودار هیوود با مثلث های صفحه فانو مطابقت دارد. همچنین، نمودار هیوود، ساختمان Tits از گروه SL 3 (F 2 ) است .

نمودار هیوود دارای شماره تقاطع 3 است و کوچکترین نمودار مکعبی با آن عدد متقاطع است (توالی A110507 در OEIS ). با احتساب نمودار هیوود، 8 نمودار مجزا از مرتبه 14 با شماره تقاطع 3 وجود دارد.

نمودار هیوود کوچکترین نمودار مکعبی با گراف کالین دو وردیر ثابت μ = 6 است . [7]

گراف هیوود یک نمودار فاصله واحد است : می توان آن را در صفحه جاسازی کرد به طوری که رئوس مجاور دقیقاً در فاصله یک فاصله از هم قرار داشته باشند، بدون اینکه دو راس در یک نقطه و هیچ راسی در نقطه ای در یک یال قرار نگیرد. [8]

ویژگی های جبری [ ویرایش ]

گروه اتومورفیسم گراف هیوود به گروه خطی پرتابی PGL 2 (7)، یک گروه از مرتبه 336 هم شکل است. بنابراین، نمودار هیوود یک نمودار متقارن است . دارای اتومورفیسم هایی است که هر راس را به هر راس دیگری و هر یال را به هر یال دیگری می برد. به‌طور قوی‌تر، نمودار هیوود 4 قوس متعدی است . [10] طبق سرشماری فاستر ، نمودار هیوود، که به عنوان F014A ارجاع شده است، تنها نمودار متقارن مکعبی در 14 راس است. [11] [12]

دارای ضخامت کتاب 3 و صف شماره 2 است . [13]

چند جمله ای مشخصه نمودار هیوود است(ایکس-3)(ایکس+3)(ایکس2-2)6. این تنها نمودار با این چند جمله ای مشخص است که آن را به نموداری تبدیل می کند که توسط طیف آن تعیین می شود.

گالری [ ویرایش ]

• 

  گذرگاه شماره 3

• 

  شاخص رنگی 3

• 

  عدد رنگی 2

• 

  تعبیه شده در یک چنبره ( نشان داده شده به صورت مربع )

• 

  تعبیه شده در یک torus (مقایسه ویدیو )

• 

  چند وجهی سیلاسی

منابع [ ویرایش ]

1. ↑ وایستاین، اریک دبلیو. "Heawood Graph" . دنیای ریاضی .
2. ^ a bپرش به بالا: Brouwer, Andries E. "Heawood graph" . اضافات و اصلاحات کتاب نمودارهای فاصله-منظم (بروور، کوهن، نویمایر؛ اسپرینگر؛ 1989)
3. ^ آبرو، م. آلدرد، REL; فانک، ام. جکسون، بیل؛ لبات، دی. Sheehan, J. (2004)، "نمودارها و نمودارها با همه 2 عامل ایزومورفیک"، مجله نظریه ترکیبی، سری B ، 92 (2): 395-404، doi : 10.1016/j.jctb.2004.09.004 ، M. 2099150 .
4. ↑ Dejter، Italo J. (2011) ، "From the Coxeter graph to the Klein graph"، Journal of Graph Theory ، 70 : 1–9، arXiv : 1002.1960 ، doi : 10.1002/jgt.20597 ، S44ID81 . .
5. ↑ براون، ازرا (2002). "اسامی متعدد از (7،3،1)" (PDF) . مجله ریاضی . 75 (2): 83-94. doi : 10.2307/3219140 . JSTOR 3219140 . بایگانی شده از نسخه اصلی (PDF) در 2012-02-05 . بازیابی 2006-10-27 .
6. ^ هیوود، پی جی (1890). "قضیه های رنگ آمیزی نقشه". فصلنامه ریاضی . سری اول. 24 : 322-339.
7. ↑ هاین وان در هولست (2006). "نمودارها و موانع در چهار بعد" (PDF) . مجله تئوری ترکیبی، سری B. 96 (3): 388-404. doi : 10.1016/j.jctb.2005.09.004 .
8. ↑ گربراخت، ابرهارد اچ.-آ. (2009). "یازده واحد تعبیه فاصله گراف هیوود". arXiv : 0912.5395 . Bibcode : 2009arXiv0912.5395G . {{cite journal}}: مجله استناد نیاز به |journal=( کمک ) دارد .
9. ^ باندی، جی . مورتی، ایالات متحده آمریکا (1976). نظریه گراف با کاربردها نیویورک: هلند شمالی. پ. 237 . شابک 0-444-19451-7. بایگانی شده از نسخه اصلی در 2010-04-13 . بازیابی شده 2019-12-18 .
10. ^ کاندر، مارستون؛ مورتون، مارگارت (1995). "طبقه بندی نمودارهای متقارن سه ظرفیتی مرتبه کوچک" (PDF) . مجله ترکیبیات استرالیایی . 11 : 146.
11. ↑ رویل، جی. "نمودارهای متقارن مکعبی (سرشماری فاستر)." بایگانی شده در 2008-07-20 در Wayback Machine
12. ↑ Conder, M. and Dobcsányi, P. "نمودارهای متقارن سه ظرفیتی تا ۷۶۸ راس." جی. ترکیب. ریاضی. ترکیب کنید. محاسبه کنید. 40، 41-63، 2002.
13. ^ جسیکا وولز، مهندسی طرح‌بندی‌های خطی با SAT . پایان نامه کارشناسی ارشد، دانشگاه توبینگن، 2018

https://en.wikipedia.org/wiki/Heawood_graph