رنگ آمیزی نمودار-

 

Graph Coloring فرایندی است که رنگها را به رئوس یک نمودار اختصاص می دهد

 

به گونه ای که به هیچ دو راس مجاور آن یک رنگ اختصاص داده نشده است.

 

  • Graph Coloring به رنگ Vertex Coloring نیز گفته می شود .
  • این تضمین می کند که هیچ لبه ای در نمودار وجود ندارد که رئوس انتهایی آن با همان رنگ رنگی باشد.
  • از چنین گرافی به عنوان نمودار رنگی مناسب نام برده می شود .

 

نمودار رنگ آمیزی نمودار-

 

نمودار زیر مثالی از نمودار به درستی رنگی است -

 

 

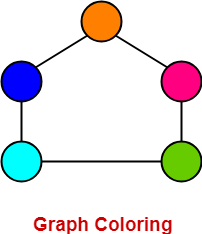
در این نمودار ،

  • هیچ دو راس مجاور با یک رنگ رنگی نیستند.
  • بنابراین ، یک نمودار رنگی مناسب است.

 

برنامه های رنگ آمیزی نمودار-

 

برخی از کاربردهای مهم رنگ آمیزی نمودار به شرح زیر است:

  • رنگ آمیزی نقشه
  • برنامه ریزی وظایف
  • تهیه جدول زمانی
  • وظیفه
  • حل تعارض
  • سودوکو

 

شماره رنگی-

 

Chromatic Number حداقل رنگ مورد نیاز برای رنگ آمیزی صحیح هر نمودار است.

 

یا

Chromatic Number حداقل رنگ مورد نیاز برای رنگ آمیزی هر نمودار است

به گونه ای که به هیچ دو راس مجاور آن یک رنگ اختصاص داده نشده است.

 

شماره اعداد رنگی-

 

نمودار زیر را در نظر بگیرید-

 

 

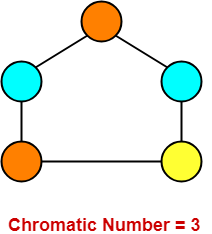
در این نمودار ،

  • هیچ دو راس مجاور با یک رنگ رنگی نیستند.
  • حداقل رنگ مورد نیاز برای رنگ آمیزی صحیح رئوس = 3.
  • بنابراین ، تعداد رنگی این نمودار = 3 است.
  • ما نمی توانیم این نمودار را به درستی با کمتر از 3 رنگ رنگ کنیم.

 

 

تعداد رنگی نمودارها-

 

تعداد رنگی برخی از انواع معمول نمودارها به شرح زیر است -

 

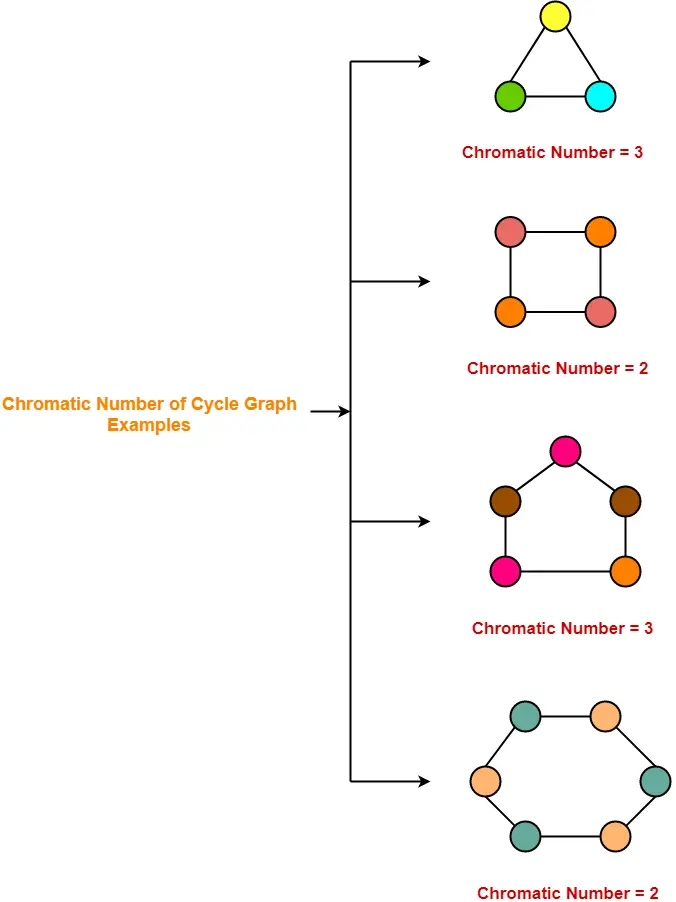
1. نمودار چرخه-

 

  • یک نمودار ساده از رئوس 'n' (n> = 3) و 'n' لبه های تشکیل دهنده یک چرخه طول 'n' به عنوان نمودار چرخه نامیده می شود.
  • در نمودار چرخه ، همه رئوس درجه 2 هستند.

 

شماره رنگی

  • اگر تعداد رئوس در نمودار چرخه زوج باشد ، عدد رنگی آن = 2 است.
  • اگر تعداد رئوس نمودار چرخه فرد باشد ، عدد رنگی آن = 3 است.

 

مثال ها-

 

 

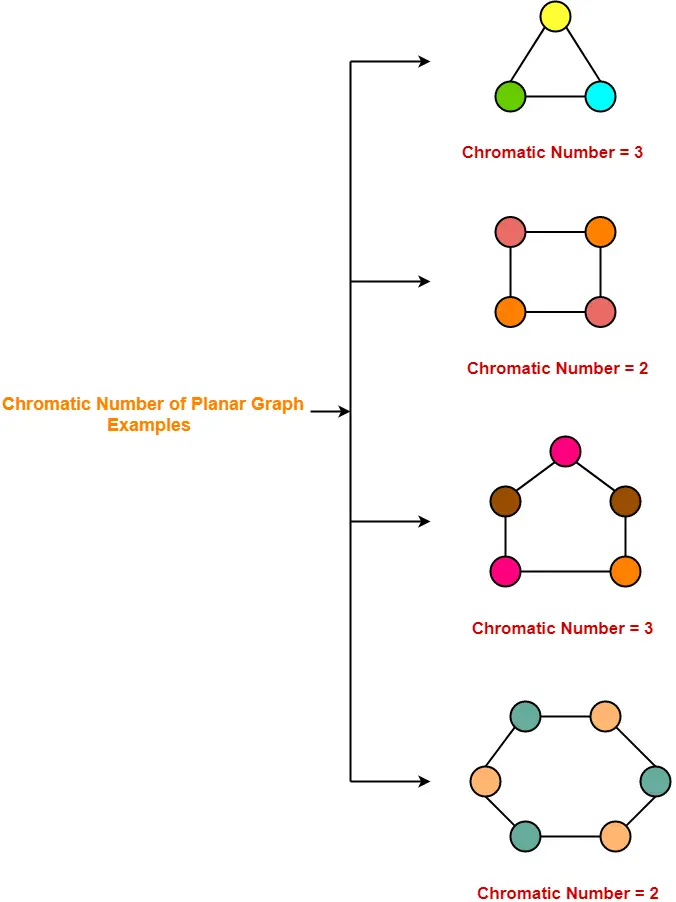
2. نمودارهای مسطح-

 

مسطح گراف یک گراف است که می توان در یک صفحه رسم کرد به طوری که هیچ یک از لبه های آن  یک دیگر قطع نمی کنند.

 

شماره رنگی

تعداد رنگی هر نمودار مسطح

= کمتر یا برابر با 4

 

مثال ها-

 

  • تمام نمودارهای چرخه فوق نیز نمودار مسطحی هستند.
  • تعداد رنگی هر نمودار کمتر یا برابر با 4 است.

 

 

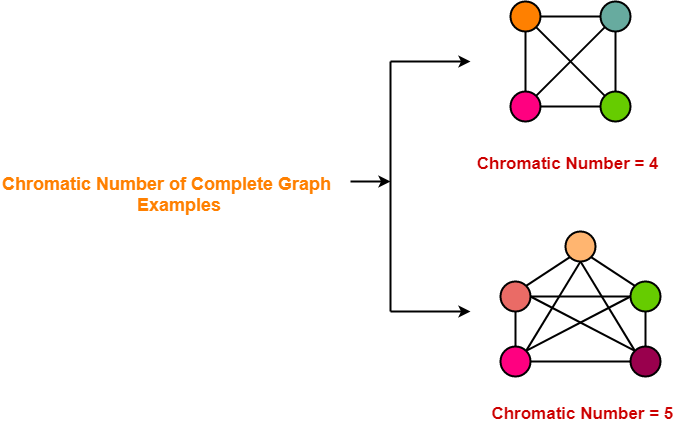
3. نمودارهای کامل-

 

  • نمودار كامل نموداري است كه در آن هر دو راس مشخص با دقيقاً يك لبه به هم متصل شوند.
  • در یک نمودار کامل ، هر راس با هر راس دیگر مرتبط است.
  • بنابراین برای درست کردن آن ، به همان تعداد رئوس رنگ مختلف در نمودار  نیاز است.

 

شماره رنگی

تعداد رنگی نمودار کامل

= تعداد رئوس آن نمودار کامل

 

مثال ها-

 

 

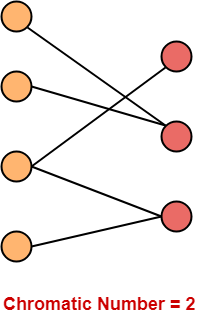
4. نمودارهای دو طرفه

 

  • دوبخشی نمودار شامل دو مجموعه از رئوس X و Y
  • لبه ها فقط رئوس X را به رئوس Y متصل می کنند ، نه راس درون یک مجموعه.

 

شماره رنگی

تعداد رنگی هر نمودار دو بخشی

= 2

 

مثال-

 

 

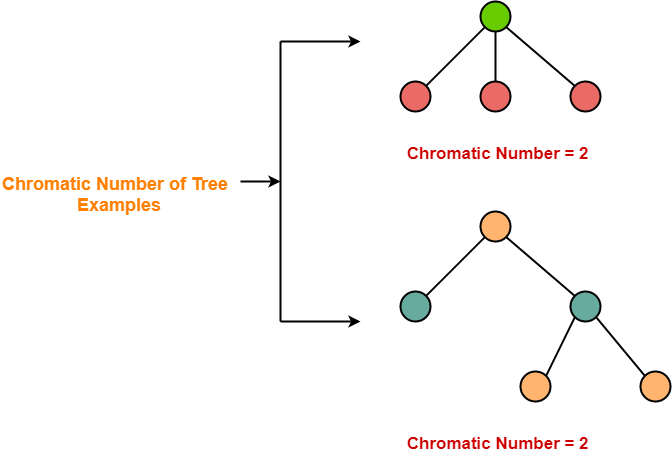
5. درختان-

 

  • درخت نوع خاصی از گراف همبند که در آن هیچ مدار وجود ندارد.
  • هر درخت یک نمودار دو بخشی است.
  • بنابراین ، تعداد رنگی یک درخت با هر تعداد راس = 2.

 

شماره رنگی

تعداد رنگی هر درخت

= 2

 

مثال ها-

 

 

خلاصه

رنگ آمیزی نمودار در تئوری نمودار | تعداد رنگی نمودارها

نام مقاله

رنگ آمیزی نمودار در تئوری نمودار | تعداد رنگی نمودارها

شرح

نمودار رنگ آمیزی در تئوری نمودار - رنگ آمیزی نمودار فرآیندی برای تعیین رنگ به رئوس است به طوری که هیچ دو راس مجاور یک رنگ نیست. Chromatic Number of a Graph حداقل تعداد رنگهای مورد نیاز برای رنگ آمیزی صحیح نمودار است.

نویسنده

آکشی سینگال

نام ناشر

دروازه ویدیالی

آرم ناشر

منبع

https://www.gatevidyalay.com/graph-coloring-chromatic-number/