تئوری گراف - تطبیق ها
نمودار منطبق ، یک زیر نمودار از نمودار است که در آن هیچ لبه مجاور یکدیگر وجود ندارد. به سادگی ، نباید هیچ راس مشترکی بین دو لبه وجود داشته باشد.
تطابق
بگذارید 'G' = (V ، E) یک نمودار باشد. به یک زیرگراف M (G) مطابق گفته می شود ، اگر هر راس G با حداکثر یک لبه در M اتفاق بیفتد ، به عنوان مثال ،
deg (V) ≤ 1 ∀ V ∈ G
این بدان معناست که در نمودار مطابق M (G) ، رئوس باید درجه 1 یا 0 داشته باشند ، جایی که لبه ها باید از نمودار G اتفاق بیفتند.
علامت گذاری - M (G)
مثال
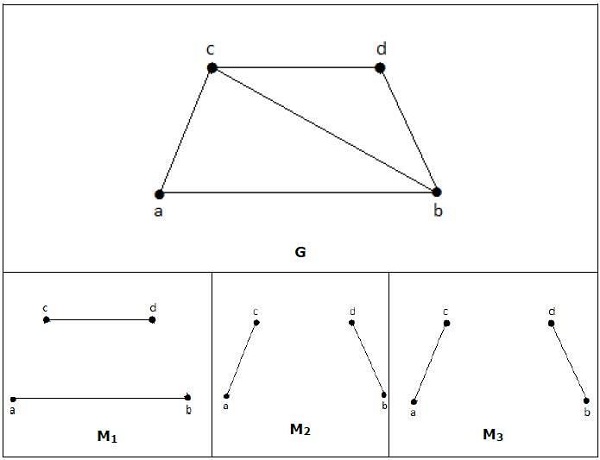
در یک تطبیق ،
اگر deg (V) = 1 ، سپس (V) گفته می شود که مطابقت دارد
اگر deg (V) = 0 ، پس از آن (V) مطابقت ندارد.
در یک تطبیق ، هیچ دو لبه مجاور نیستند. به این دلیل که اگر هر دو لبه در مجاورت یکدیگر باشند ، در این صورت درجه راس که به آن دو لبه می پیوندد دارای درجه 2 خواهد بود که قانون تطبیق را نقض می کند.
تطبیق حداکثر
اگر هیچ لبه دیگری از "G" به M اضافه نشود ، یک M منطبق از نمودار "G" به حداکثر گفته می شود .
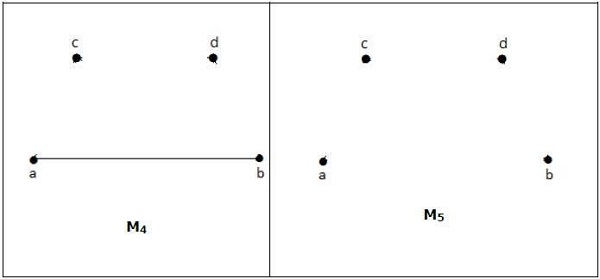
مثال
M1 ، M2 ، M3 از نمودار بالا حداکثر مطابقت G است.
حداکثر تطبیق
همچنین به عنوان بزرگترین تطبیق حداکثر شناخته می شود. حداکثر تطبیق به عنوان حداکثر تطبیق با حداکثر تعداد لبه ها تعریف می شود.
به تعداد لبه ها در حداکثر تطبیق "G" عدد مطابقت آن گفته می شود .
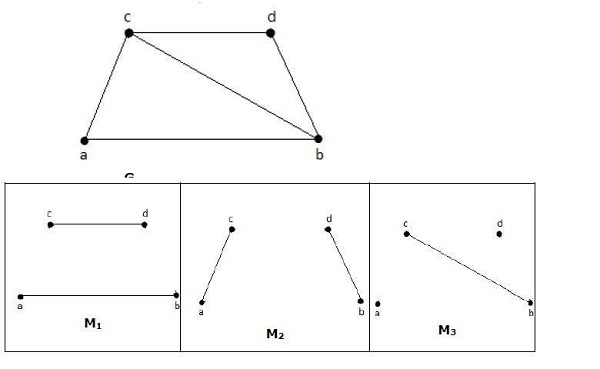
مثال
برای نمودار ارائه شده در مثال فوق ، M1 و M2 حداکثر مطابقت "G" و عدد مطابقت آن 2 است. از این رو با استفاده از نمودار G ، ما فقط می توانیم زیرگرافها را فقط با حداکثر 2 لبه تشکیل دهیم. از این رو عدد تطبیق را دو داریم.
تطبیق کامل
مطابقت (M) نمودار (G) مطابقت کامل دارد ، اگر هر راس نمودار g (G) دقیقاً به یک لبه مطابقت (M) برخورد کند ، به عنوان مثال ،
deg (V) = 1 V
درجه هر راس در زیرگراف باید درجه 1 باشد.
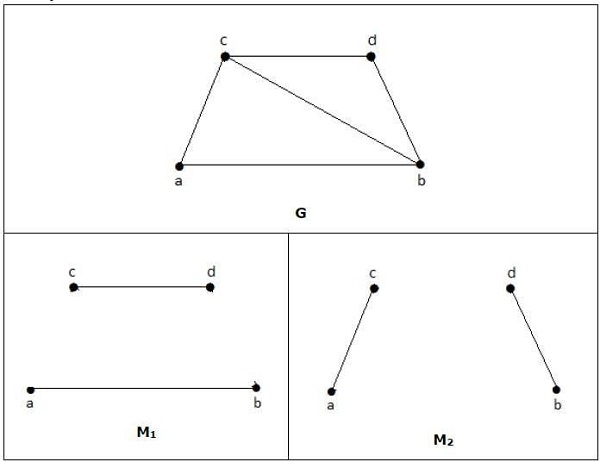
مثال
در نمودارهای زیر ، M1 و M2 نمونه هایی از مطابقت کامل G است.
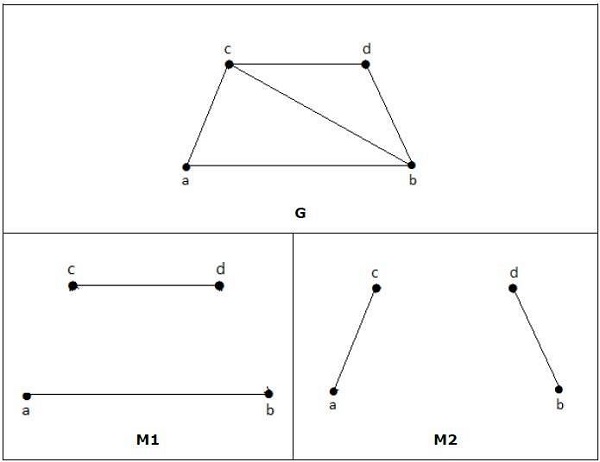
توجه - هر تطبیق کامل نمودار همچنین یک تطبیق حداکثر نمودار است ، زیرا هیچ فرصتی برای اضافه کردن یک لبه دیگر در یک نمودار تطبیق کامل وجود ندارد.
حداکثر مطابقت نمودار لازم نیست کامل باشد. اگر نمودار 'G' مطابقت کامل داشته باشد ، تعداد رئوس | V (G) | یکنواخت است اگر فرد باشد ، آخرین راس با راس دیگر جفت می شود و در آخر یک راس واحد باقی می ماند که نمی تواند با هیچ راس دیگری که درجه آن صفر است جفت شود. این کاملاً منطبق بر اصل تطبیق کامل است
مثال
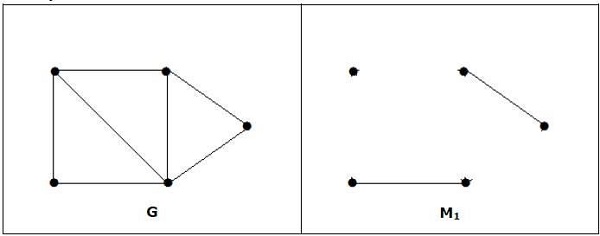
توجه - معکوس جمله فوق الذکر صحیح نیست. اگر G دارای راسهای زوج باشد ، M1 نیازی به کامل بودن ندارد.
مثال
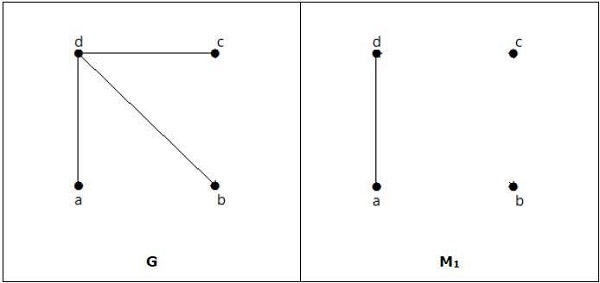
مطابقت دارد ، اما مطابقت کاملی ندارد ، حتی اگر تعداد راسهای زوجی داشته باشد.
منبع
https://www.tutorialspoint.com/graph_theory/graph_theory_matchings.htm
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.