ریاضیات

مسئله های  عملی مبتنی بر راه رفتن در تئوری گراف -

مسئله -01:

نمودار زیر را در نظر بگیرید-

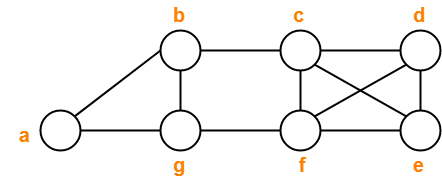
تصمیم بگیرید که کدام یک از توالی های رئوس زیر راه رفتن را تعیین می کند.

برای کسانی که پیاده روی هستند ، تصمیم بگیرید که این یک مدار است ، یک مسیر ، یک چرخه یا یک مسیر.

1. a ، b ، g ، f ، c ، b
2. b ، g ، f ، c ، b ، g ، a
3. c ، e ، f ، c
4. c ، e ، f ، c ، e
5. a ، b ، f ، a
6. f ، d ، e ، c ، b

راه حل-

1. دنباله
2. راه رفتن
3. چرخه
4. راه رفتن
5. پیاده روی نیست
6. مسیر

مسئله 02:

نمودار زیر را در نظر بگیرید-

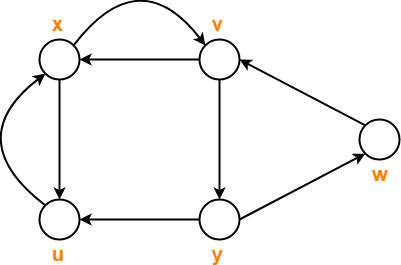
دنباله های زیر راس ها را در نظر بگیرید و به س questionsالات زیر پاسخ دهید

1. x ، v ، y ، w ، v
2. x ، u ، x ، u ، x
3. x ، u ، v ، y ، x
4. x ، v ، y ، w ، v ، u ، x

1. کدام یک از توالی های فوق الذکر پیاده روی کارگردانی هستند؟
2. طول پیاده روی های مستقیم چند است؟
3. کدام پیاده روی های مستقیم مسیرهای هدایت شده ای نیز هستند؟
4. کدام پیاده روی های مستقیم نیز چرخه های کارگردانی هستند؟

راه حل-

قسمت 01:

• فقط (A) و (B) پیاده روی های مستقیم هستند.
• (C) یک پیاده روی مستقیم نیست زیرا هیچ قوسی از راس u به راس v وجود ندارد.
• (D) یک پیاده روی مستقیم نیست زیرا هیچ قوسی از راس v به راس u وجود ندارد.

قسمت 02:

طول هر دو مسیر (A) و (B) دارای طول = 4 هستند.

قسمت 03:

• نه (A) و نه (B) مسیرهای هدایت شده ای نیستند.
• این به این دلیل است که رئوس در هر دو تکرار می شوند.
• Vertex v در Walk (A) و vertex u در Walk (B) تکرار می شود.

قسمت 04:

• هیچ یک از آنها چرخه های کارگردانی نیستند.
• Walk (A) چرخه مستقیمی را نشان نمی دهد زیرا رئوس شروع و پایان آن یکسان نیستند.
• Walk (B) چرخه مستقیمی را نشان نمی دهد زیرا رئوس / لبه ها را تکرار می کند.

مسئله -03:

نمودار زیر را در نظر بگیرید-

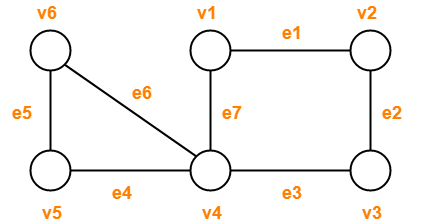
توالی های داده شده را مشاهده کنید و ماهیت پیاده روی را در هر مورد پیش بینی کنید -

1. v1e1v2e2v3e2v2
2. v4e7v1e1v2e2v3e3v4e4v5
3. v1e1v2e2v3e3v4e4v5
4. v1e1v2e2v3e3v4e7v1
5. v6e5v5e4v4e3v3e2v2e1v1e7v4e6v6

راه حل-

1. پیاده روی باز
2. دنباله (مسیر نیست زیرا vertex v4 تکرار می شود)
3. مسیر
4. چرخه
5. مدار (چرخه نیست زیرا vertex v4 تکرار می شود)