​

مقادیر ویژه و توابع ویژه عملگرهای دیفرانسیل

[ ویرایش ]

مقاله اصلی: توابع ویژه

تعاریف مقدار ویژه و بردارهای ویژه یک تبدیل خطی T حتی اگر فضای برداری زیربنایی یک فضای بی‌بعد هیلبرت یا باناخ باشد، معتبر باقی می‌ماند . دسته‌ای از تبدیل‌های خطی پرکاربرد که بر روی فضاهای بی‌بعدی عمل می‌کنند، عملگرهای دیفرانسیل در فضاهای تابعی هستند . فرض کنید D یک عملگر دیفرانسیل خطی در فضای C ∞ از توابع حقیقی بی نهایت متفاوت یک آرگومان حقیقی t باشد . معادله مقدار ویژه برای D معادله دیفرانسیل است

{\displaystyle Df(t)=\lambda f(t)}

توابعی که این معادله را برآورده می کنند بردارهای ویژه D هستند و معمولاً به آنها توابع ویژه می گویند .

مثال عملگر مشتق

[ ویرایش ]

عملگر مشتق را در نظر بگیرید{\displaystyle {\tfrac {d}{dt}}}با معادله ارزش ویژه

{\displaystyle {\frac {d}{dt}}f(t)=\lambda f(t).}

این معادله دیفرانسیل را می توان با ضرب هر دو طرف در dt / f ( t ) و ادغام حل کرد . راه حل آن، تابع نمایی

{\displaystyle f(t)=f(0)e^{\lambda t},}تابع ویژه عملگر مشتق است. در این مورد، تابع ویژه خود تابعی از مقدار ویژه مرتبط با آن است. به طور خاص، برای λ = 0، تابع ویژه f ( t ) یک ثابت است.

مقاله تابع اصلی مثال‌های دیگری ارائه می‌کند.

تعریف کلی

[ ویرایش ]

مفهوم مقادیر ویژه و بردارهای ویژه به طور طبیعی به تبدیل های خطی دلخواه در فضاهای برداری دلخواه گسترش می یابد. فرض کنید V یک فضای برداری بر روی یک میدان K از اسکالرها باشد ، و اجازه دهید T یک تبدیل خطی باشد که V را به V نگاشت ،{\displaystyle T:V\to V.}

ما می گوییم که یک بردار غیرصفر v ∈ V بردار ویژه T است اگر و فقط در صورتی که یک عدد اسکالر λ ∈ K وجود داشته باشد به طوری که

{\displaystyle T(\mathbf {v} )=\lambda \mathbf {v}.} ( 5 )

این معادله معادله مقدار ویژه برای T نامیده می شود و λ اسکالر مقدار ویژه T مربوط به بردار ویژه v است . T ( v ) نتیجه اعمال تبدیل T به بردار v است ، در حالی که λ v حاصلضرب λ اسکالر با v است . [ 37 ] [ 38 ]

فضاهای ویژه، کثرت هندسی و پایه ویژه

[ ویرایش ]

با توجه به مقدار ویژه λ ، مجموعه را در نظر بگیرید

{\displaystyle E=\left\{\mathbf {v} :T(\mathbf {v} )=\lambda \mathbf {v} \راست\}،}

که اتحاد بردار صفر با مجموعه تمام بردارهای ویژه مرتبط با λ است . E فضای ویژه یا فضای مشخصه T مرتبط با λ نامیده می شود . [ 39 ]

با تعریف تبدیل خطی

{\displaystyle {\begin{aligned}T(\mathbf {x} +\mathbf {y})&=T(\mathbf {x})+T(\mathbf {y})،\\T(\alpha \ mathbf {x} )&=\alpha T(\mathbf {x})،\end{تراز شده}}}

برای x , y ∈ V و α ∈ K . بنابراین، اگر u و v بردارهای ویژه T مرتبط با مقدار ویژه λ ، یعنی u ، v ∈ E باشند ، آنگاه

{\displaystyle {\begin{aligned}T(\mathbf {u} +\mathbf {v} )&=\lambda (\mathbf {u} +\mathbf {v})،\\T(\alpha \mathbf { v} )&=\lambda (\alpha \mathbf {v}).\end{تراز شده}}}

بنابراین، u + v و α v یا صفر هستند یا بردارهای ویژه T مرتبط با λ ، یعنی u + v ، α v ∈ E ، و E تحت جمع و ضرب اسکالر بسته است. بنابراین فضای ویژه E مرتبط با λ یک زیرفضای خطی از V است . [ 40 ] اگر آن زیرفضا بعد 1 داشته باشد، گاهی اوقات به آن خط ویژه می گویند . [ 41 ]

تعدد هندسی γT ( λ ) یک مقدار ویژه λ بعد فضای ویژه مرتبط با λ است ، یعنی حداکثر تعداد بردارهای ویژه مستقل خطی مرتبط با آن مقدار ویژه. [ 9 ] [ 26 ] [ 42 ] با تعریف مقادیر ویژه و بردارهای ویژه، γT ( λ ) ≥ 1 است زیرا هر مقدار ویژه حداقل یک بردار ویژه دارد.

فضاهای ویژه T همیشه یک جمع مستقیم را تشکیل می دهند . در نتیجه، بردارهای ویژه مقادیر ویژه مختلف همیشه به صورت خطی مستقل هستند. بنابراین، مجموع ابعاد فضاهای ویژه نمی تواند از بعد n فضای برداری که T روی آن عمل می کند بیشتر شود و نمی تواند بیش از n مقدار ویژه مجزا وجود داشته باشد. [ د ]

هر زیرفضایی که توسط بردارهای ویژه T قرار گرفته باشد ، یک زیرفضای غیرمتغیر T است و محدودیت T به چنین زیرفضایی قابل قطریابی است. علاوه بر این، اگر کل فضای برداری V را بتوان توسط بردارهای ویژه T در بر گرفت ، یا به طور معادل اگر مجموع مستقیم فضاهای ویژه مرتبط با تمام مقادیر ویژه T کل فضای برداری V باشد، می توان مبنایی از V به نام پایه ویژه ایجاد کرد. از بردارهای ویژه مستقل خطی T تشکیل شده است . وقتی T یک پایه ویژه را می پذیرد، T قابل قطری است.

نظریه طیفی

[ ویرایش ]

مقاله اصلی: نظریه طیفی

اگر λ یک مقدار ویژه از T باشد ، عملگر ( T - λI ) یک به یک نیست و بنابراین معکوس آن ( T - λI )^-1 وجود ندارد. این عکس برای فضاهای برداری با ابعاد محدود صادق است، اما برای فضاهای برداری بی‌بعدی صادق نیست. به طور کلی، عملگر ( T - λI ) ممکن است معکوس نداشته باشد حتی اگر λ یک مقدار ویژه نباشد.

به همین دلیل، در تحلیل تابعی، مقادیر ویژه را می توان به طیف یک عملگر خطی T به عنوان مجموعه ای از همه اسکالرهای λ تعمیم داد که عملگر ( T - λI ) هیچ معکوس محدودی ندارد . طیف یک عملگر همیشه شامل تمام مقادیر ویژه آن است اما محدود به آنها نیست.

جبرهای انجمنی و نظریه نمایش

[ ویرایش ]

مقاله اصلی: وزن (نظریه نمایش)

می‌توان شی جبری را که روی فضای برداری عمل می‌کند تعمیم داد، و یک عملگر منفرد را که روی یک فضای برداری عمل می‌کند با یک نمایش جبری - یک جبر انجمنی که روی یک مدول عمل می‌کند، جایگزین کرد . مطالعه چنین اقداماتی حوزه نظریه نمایش است .

مفهوم تئوریک نمایش وزن، آنالوگ مقادیر ویژه است، در حالی که بردارهای وزن و فضاهای وزنی به ترتیب آنالوگ بردارهای ویژه و فضاهای ویژه هستند.

هکه شیف ویژه یک تانسور چندگانه از خودش است و در مکاتبات لنگ لاندز در نظر گرفته می شود .

معادلات دینامیک

[ ویرایش ]

ساده ترین معادلات تفاوت شکل دارند

{\displaystyle x_{t}=a_{1}x_{t-1}+a_{2}x_{t-2}+\cdots +a_{k}x_{tk}.}

حل این معادله برای x بر حسب t با استفاده از معادله مشخصه آن به دست می آید

{\displaystyle \lambda ^{k}-a_{1}\lambda ^{k-1}-a_{2}\lambda ^{k-2}-\cdots -a_{k-1}\lambda -a_{ k}=0،}

که با چیدن در ماتریس مجموعه ای از معادلات متشکل از معادله تفاوت فوق و معادلات k – 1 پیدا می شود.

{\displaystyle x_{t-1}=x_{t-1},\ \dots ,\ x_{t-k+1}=x_{t-k+1},}یک سیستم k بعدی مرتبه اول در بردار متغیر انباشته داده می شود

{\displaystyle {\begin{bmatrix}x_{t}&\cdots &x_{t-k+1}\end{bmatrix}}}بر حسب مقدار یک بار تاخیر آن و با در نظر گرفتن معادله مشخصه ماتریس این سیستم. این معادله k ریشه مشخصه می دهدλ1،…،λک،{\displaystyle \lambda _{1},\,\ldots ,\,\lambda _{k},}برای استفاده در معادله حل

{\displaystyle x_{t}=c_{1}\lambda _{1}^{t}+\cdots +c_{k}\lambda _{k}^{t}.}

یک روش مشابه برای حل یک معادله دیفرانسیل از فرم استفاده می شود

{\displaystyle {\frac {d^{k}x}{dt^{k}}}+a_{k-1}{\frac {d^{k-1}x}{dt^{k-1} }}+\cdots +a_{1}{\frac {dx}{dt}}+a_{0}x=0.}

محاسبه

[ ویرایش ]

مقاله اصلی: الگوریتم مقدار ویژه

محاسبه مقادیر ویژه و بردارهای ویژه موضوعی است که در آن نظریه، همانطور که در کتاب های درسی جبر خطی ابتدایی ارائه شده است، اغلب از عمل بسیار دور است.

روش کلاسیک

[ ویرایش ]

روش کلاسیک این است که ابتدا مقادیر ویژه را پیدا کنید و سپس بردارهای ویژه را برای هر مقدار ویژه محاسبه کنید. از چند جهت برای محاسبات غیردقیق مانند ممیز شناور مناسب نیست .

مقادیر ویژه

[ ویرایش ]

مقادیر ویژه یک ماتریس{\displaystyle A}را می توان با یافتن ریشه های چند جمله ای مشخصه تعیین کرد. این برای ×ماتریس، اما دشواری به سرعت با اندازه ماتریس افزایش می یابد.

در تئوری، ضرایب چند جمله ای مشخصه را می توان دقیقاً محاسبه کرد، زیرا آنها مجموع حاصل از عناصر ماتریس هستند. و الگوریتم‌هایی وجود دارند که می‌توانند تمام ریشه‌های یک چند جمله‌ای با درجه دلخواه را با دقت لازم پیدا کنند . [ 43 ] با این حال، این رویکرد در عمل قابل دوام نیست زیرا ضرایب توسط خطاهای گرد کردن اجتناب ناپذیر آلوده می شوند ، و ریشه های یک چند جمله ای می توانند تابع بسیار حساس ضرایب باشند (همانطور که در چند جمله ای ویلکینسون نشان داده شده است ). [ 43 ] حتی برای ماتریس هایی که عناصر آنها اعداد صحیح هستند، محاسبه غیر ضروری می شود، زیرا مجموع آن ها بسیار طولانی است. جمله ثابت تعیین کننده است که برای یک{\displaystyle n\times n}ماتریس مجموع است{\displaystyle n!}ضربهای مختلف [ e ]

فرمول‌های جبری صریح برای ریشه‌های یک چند جمله‌ای تنها در صورتی وجود دارند که درجه باشند {\displaystyle n}4 یا کمتر است. طبق قضیه آبل-روفینی هیچ فرمول جبری کلی، صریح و دقیقی برای ریشه های یک چند جمله ای با درجه 5 یا بیشتر وجود ندارد. (کلییت مهم است زیرا هر چند جمله ای با درجهn{\displaystyle n}چند جمله ای مشخصه برخی از ماتریس های مرتبه استn{\displaystyle n}.) بنابراین، برای ماتریس های مرتبه 5 یا بیشتر، مقادیر ویژه و بردارهای ویژه را نمی توان با یک فرمول جبری صریح به دست آورد، بنابراین باید با روش های عددی تقریبی محاسبه شوند . حتی فرمول دقیق برای ریشه های یک چند جمله ای درجه 3 از نظر عددی غیر عملی است.

بردارهای ویژه

[ ویرایش ]

هنگامی که مقدار (دقیق) یک مقدار ویژه مشخص شد، بردارهای ویژه مربوطه را می توان با یافتن جواب های غیرصفر معادله مقدار ویژه یافت، که تبدیل به سیستمی از معادلات خطی با ضرایب شناخته شده می شود. به عنوان مثال، زمانی که مشخص شد 6 یک مقدار ویژه ماتریس است

{\displaystyle A={\begin{bmatrix}4&1\\6&3\end{bmatrix}}}

با حل معادله می توانیم بردارهای ویژه آن را پیدا کنیم

{\displaystyle Av=6v}، یعنی

{\displaystyle {\begin{bmatrix}4&1\\6&3\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}=6\cdot {\begin{bmatrix}x\\y\ پایان{bmatrix}}}

این معادله ماتریسی معادل دو معادله خطی است

{\displaystyle \left\{{\begin{aligned}4x+y&=6x\\6x+3y&=6y\end{aligned}}\right.} یعنی

{\displaystyle \left\{{\begin{aligned}-2x+y&=0\\6x-3y&=0\end{aligned}}\right.}

هر دو معادله به یک معادله خطی کاهش می یابد

{\displaystyle y=2x}. بنابراین، هر بردار از فرم

{\displaystyle {\begin{bmatrix}a&2a\end{bmatrix}}^{\textsf {T}}}، برای هر عدد حقیقی غیر صفر{\displaystyle a}، بردار ویژه ای از{\displaystyle A}با ارزش ویژه

{\displaystyle \lambda =6}.

ماتریس {\displaystyle A}بالا یک مقدار ویژه دیگر دارد{\displaystyle \lambda =1}. یک محاسبه مشابه نشان می دهد که بردارهای ویژه مربوطه، راه حل های غیر صفر هستند{\displaystyle 3x+y=0}، یعنی هر بردار فرم{\displaystyle {\begin{bmatrix}b&-3b\end{bmatrix}}^{\textsf {T}}}، برای هر عدد حقیقی غیر صفر {\displaystyle b}.

روش های تکراری ساده

[ ویرایش ]

مقاله اصلی: تکرار قدرت

رویکرد معکوس، یعنی ابتدا جستجوی بردارهای ویژه و سپس تعیین هر مقدار ویژه از بردار ویژه آن، برای کامپیوترها بسیار قابل قبول تر است. ساده ترین الگوریتم در اینجا شامل انتخاب یک بردار شروع دلخواه و سپس ضرب مکرر آن با ماتریس (به طور اختیاری عادی سازی بردار برای حفظ عناصر آن در اندازه معقول) است. این باعث می شود که بردار به سمت یک بردار ویژه همگرا شود. یک تغییر این است که در عوض بردار را در ضرب کنیم

{\displaystyle (A-\mu I)^{-1}}; این باعث می شود که به بردار ویژه نزدیکترین مقدار ویژه همگرا شود

{\displaystyle \mu \in \mathbb {C} }.

اگرv{\displaystyle \mathbf {v} }(تقریبی خوب از) بردار ویژه است{\displaystyle A}، سپس مقدار ویژه مربوطه را می توان به صورت محاسبه کرد

{\displaystyle \lambda ={\frac {\mathbf {v} ^{*}A\mathbf {v} }{\mathbf {v} ^{*}\mathbf {v} }}}

که{\displaystyle \mathbf {v} ^{*}}نشان دهنده جابجایی مزدوج است{\displaystyle \mathbf {v} }.

روش های مدرن

[ ویرایش ]

روش‌های کارآمد و دقیق برای محاسبه مقادیر ویژه و بردارهای ویژه ماتریس‌های دلخواه تا زمانی که الگوریتم QR در سال 1961 طراحی شد، شناخته نشده بود . [ نیاز به منبع ] برای ماتریس‌های پراکنده هرمیتی بزرگ ، الگوریتم لانکزوس یکی از نمونه‌های روش تکراری کارآمد برای محاسبه مقادیر ویژه و بردارهای ویژه، در میان چندین احتمال دیگر است. [ 43 ]

اکثر روش‌های عددی که مقادیر ویژه یک ماتریس را محاسبه می‌کنند، مجموعه‌ای از بردارهای ویژه متناظر را نیز به عنوان ضرب فرعی محاسبه تعیین می‌کنند، اگرچه گاهی اوقات پیاده‌کننده‌ها تصمیم می‌گیرند که اطلاعات بردار ویژه را به محض اینکه دیگر مورد نیاز نباشد، کنار بگذارند.

برنامه های کاربردی

[ ویرایش ]

تحولات هندسی

[ ویرایش ]

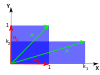
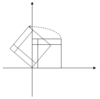
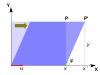
بردارهای ویژه و مقادیر ویژه می توانند برای درک تبدیل خطی اشکال هندسی مفید باشند. جدول زیر چند نمونه تبدیل در صفحه را به همراه ماتریس های 2×2، مقادیر ویژه و بردارهای ویژه آنها ارائه می دهد.

مقادیر ویژه تبدیلات هندسی

مقیاس بندیمقیاس بندی نابرابرچرخش برش افقیچرخش هایپربولیک

تصویرسازیمقیاس بندی برابر (همسانی)انقباض عمودی و کشش افقی یک مربع واحد.چرخش 50 درجه

نقشه برداری برشی افقی

ماتریس{\displaystyle {\begin{bmatrix}k&0\\0&k\end{bmatrix}}}{\displaystyle {\begin{bmatrix}k_{1}&0\\0&k_{2}\end{bmatrix}}}{\displaystyle {\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}{\displaystyle {\begin{bmatrix}1&k\\0&1\end{bmatrix}}}{\displaystyle {\begin{bmatrix}\cosh \varphi &\sinh \varphi \\\sinh \varphi &\cosh \varphi \end{bmatrix}}}


چند جمله ای مشخصه{\displaystyle \ (\lambda -k)^{2}}{\displaystyle (\lambda -k_{1})(\lambda -k_{2})}{\displaystyle \lambda ^{2}-2\cos(\theta )\lambda +1}

{\displaystyle \ (\lambda -1)^{2}}{\displaystyle \lambda ^{2}-2\cosh(\varphi )\lambda +1}

مقادیر ویژه،{\displaystyle \lambda _{i}}{\displaystyle \lambda _{1}=\lambda _{2}=k}{\displaystyle {\begin{aligned}\lambda _{1}&=k_{1}\\\lambda _{2}&=k_{2}\end{aligned}}}{\displaystyle {\begin{aligned}\lambda _{1}&=e^{i\theta }\\&=\cos \theta +i\sin \theta \\\lambda _{2}&=e^ {-i\theta }\\&=\cos \theta -i\sin \theta \end{aligned}}}{\displaystyle \lambda _{1}=\lambda _{2}=1}{\displaystyle {\begin{aligned}\lambda _{1}&=e^{\varphi }\\&=\cosh \varphi +\sinh \varphi \\\lambda _{2}&=e^{- \varphi }\\&=\cosh \varphi -\sinh \varphi \end{تراز شده}}}

مولتی جبری ،
{\displaystyle \mu _{i}=\mu (\lambda _{i})}{\displaystyle \mu _{1}=2}{\displaystyle {\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}}{\displaystyle {\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}}{\displaystyle \mu _{1}=2}{\displaystyle {\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}}

مولتی هندسی ،
{\displaystyle \gamma _{i}=\gamma (\lambda _{i})}{\displaystyle \gamma _{1}=2}{\displaystyle {\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}}{\displaystyle {\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}}{\displaystyle \gamma _{1}=1}{\displaystyle {\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}}

بردارهای ویژه همه بردارهای غیر صفر{\displaystyle {\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\0\end{bmatrix}}\\\mathbf {u} _{2}&={ \begin{bmatrix}0\\1\end{bmatrix}}\end{تراز شده}}}{\displaystyle {\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\-i\end{bmatrix}}\\\mathbf {u} _{2}&= {\begin{bmatrix}1\\+i\end{bmatrix}}\end{aligned}}}{\displaystyle \mathbf {u} _{1}={\begin{bmatrix}1\\0\end{bmatrix}}}{\displaystyle {\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\1\end{bmatrix}}\\\mathbf {u} _{2}&={ \begin{bmatrix}1\\-1\end{bmatrix}}\end{تراز شده}}}

معادله مشخصه یک چرخش یک معادله درجه دوم با تفکیک است

{\displaystyle D=-4(\sin \theta )^{2}}، که هرگاه θ مضرب صحیح 180 درجه نباشد یک عدد منفی است . بنابراین، به جز این موارد خاص، دو مقدار ویژه اعداد مختلط هستند.

{\displaystyle \cos \theta \pm i\sin \theta }; و همه بردارهای ویژه دارای ورودی های غیر حقیقی هستند. در واقع، به جز موارد خاص، یک چرخش جهت هر بردار غیر صفر را در صفحه تغییر می دهد.

یک تبدیل خطی که یک مربع را به یک مستطیل از همان ناحیه می برد ( نگاشت فشرده ) دارای مقادیر ویژه متقابل است.

تجزیه و تحلیل مؤلفه های اصلی

[ ویرایش ]

PCA توزیع گاوسی چند متغیره با محوریت{\displaystyle (1،3)}با انحراف استاندارد 3 در تقریبا{\displaystyle (0.878,0.478)}جهت و از 1 در جهت متعامد. بردارهای نشان داده شده بردارهای ویژه واحدی از ماتریس کوواریانس (متقارن، مثبت-نیمه معین) هستند که با جذر مقدار ویژه مربوطه مقیاس شده اند. همانطور که در حالت تک بعدی، جذر گرفته می شود زیرا انحراف معیار به راحتی قابل مشاهده است تا واریانس .

مقاله اصلی: تحلیل مؤلفه های اصلی

همچنین ببینید: ماتریس نیمه معین مثبت و تحلیل عاملی

تجزیه ویژه یک ماتریس نیمه معین مثبت متقارن (PSD) مبنایی متعامد از بردارهای ویژه را به دست می دهد که هر کدام دارای یک مقدار ویژه غیرمنفی هستند. تجزیه متعامد یک ماتریس PSD در تجزیه و تحلیل چند متغیره استفاده می شود ، که در آن ماتریس های کوواریانس نمونه PSD هستند. این تجزیه متعامد در آمار، آنالیز مؤلفه اصلی (PCA) نامیده می شود. PCA روابط خطی بین متغیرها را مطالعه می کند. PCA بر روی ماتریس کوواریانس یا ماتریس همبستگی (که در آن هر متغیر برای داشتن واریانس نمونه آن برابر با یک مقیاس بندی می شود) انجام می شود . برای ماتریس کوواریانس یا همبستگی، بردارهای ویژه با مؤلفه های اصلی و مقادیر ویژه به واریانس توضیح داده شده توسط مؤلفه های اصلی مطابقت دارند. تجزیه و تحلیل مؤلفه اصلی ماتریس همبستگی یک مبنای متعامد برای فضای داده‌های مشاهده‌شده فراهم می‌کند: بر این اساس، بزرگترین مقادیر ویژه مربوط به مؤلفه‌های اصلی است که با بیشتر هم‌واریایی‌پذیری در میان تعدادی از داده‌های مشاهده‌شده مرتبط است.

تجزیه و تحلیل مؤلفه های اصلی به عنوان ابزاری برای کاهش ابعاد در مطالعه مجموعه داده های بزرگ ، مانند آنهایی که در بیوانفورماتیک با آن مواجه می شوند، استفاده می شود . در روش Q ، مقادیر ویژه ماتریس همبستگی، قضاوت روش‌شناس Q را در مورد اهمیت عملی تعیین می‌کند (که با اهمیت آماری آزمون فرضیه متفاوت است ؛ معیارهای تعیین تعداد عوامل را رجوع کنید ). به طور کلی، تحلیل مؤلفه های اصلی می تواند به عنوان روشی برای تحلیل عاملی در مدل سازی معادلات ساختاری استفاده شود .

​