ماتریس هرمیتین یا خود الحاقی

توسط علی رضا نقش نیلچی | یکشنبه بیست و یکم خرداد ۱۴۰۲ | 1:58

ماتریس هرمیتین یا خود الحاقی

در این پست متوجه خواهید شد که ماتریس هرمیتی چیست که به عنوان ماتریس خود الحاقی نیز شناخته می شود. نمونه‌هایی از ماتریس‌های هرمیتی، تمام خواص و فرمول آن را خواهید یافت. در نهایت، نحوه تجزیه هر ماتریس مختلط را به مجموع یک ماتریس هرمیتی به اضافه یک ماتریس اریب-هرمیتی توضیح می دهیم.

فهرست مطالب

ماتریس هرمیتین (یا خود الحاقی) چیست؟
نمونه هایی از ماتریس های هرمیتی
خواص ماتریس هرمیت
فرمول ماتریس هرمیتی
تجزیه یک ماتریس مختلط به یک ماتریس هرمیتی و یک ماتریس کج-هرمیتی

ماتریس هرمیتین (یا خود الحاقی) چیست؟

تعریف ماتریس هرمیتی به شرح زیر است:

ماتریس هرمیتی یا ماتریس خود الحاقی نیز نامیده می شود، ماتریس مربعی با اعداد مختلط است که مشخصه برابری با ترانهاده مزدوج آن را دارد. بنابراین، همه ماتریس های هرمیت دارای شرایط زیر هستند:

A=A^H

جایی که A H ترانهاده مزدوج ماتریس A است.

ببینید: چگونه می توان ترانهاده مزدوج مختلط یک ماتریس را پیدا کرد.

جالب اینجاست که این نوع ماتریس به افتخار چارلز هرمیت، ریاضیدان فرانسوی قرن نوزدهم که تحقیقات مهمی در ریاضیات، به ویژه در زمینه جبر خطی انجام داد، نامگذاری شده است.

دلیل نامگذاری این ماتریس این بود که او نشان داد که مقادیر ویژه این ماتریس های عجیب و غریب همیشه اعداد حقیقی هستند، اما در زیر در ویژگی های ماتریس های هرمیتی به تفصیل توضیح خواهیم داد.

نمونه هایی از ماتریس های هرمیتی

هنگامی که معنای ماتریس هرمیتی (یا ماتریس خود الحاقی) را دیدیم، بیایید چند نمونه از ماتریس های هرمیتی با ابعاد مختلف را ببینیم:

نمونه ای از ماتریس هرمیتی با ابعاد 2×2

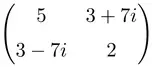
نمونه ای از یک ماتریس هرمیتی با ابعاد 2x2

نمونه ای از ماتریس هرمیتی با ابعاد 3×3

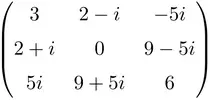
نمونه ای از ماتریس هرمیتی با ابعاد 3x3

نمونه ای از ماتریس هرمیتی با ابعاد 4×4

نمونه ای از ماتریس هرمیتی با ابعاد 4*4

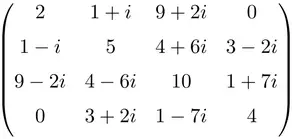
همه این ماتریس ها هرمیتی هستند زیرا ترانهاده مزدوج هر ماتریس برابر با خود هر ماتریس است.

خواص ماتریس هرمیت

ماتریس های هرمیت دارای ویژگی های زیر هستند:

هر ماتریس هرمیتی یک ماتریس معمولی است. اگرچه همه ماتریس های نرمال ماتریس هرمیتی نیستند.

هر ماتریس هرمیتی با یک ماتریس واحد قابل قطریابی است. همچنین، ماتریس قطری به دست آمده فقط شامل عناصر حقیقی است.

بنابراین، مقادیر ویژه یک ماتریس هرمیتی همیشه اعداد حقیقی هستند. این ویژگی توسط چارلز هرمیت کشف شد و به همین دلیل او را با نامیدن این ماتریس بسیار خاص هرمیتیان مفتخر کرد.

یک ماتریس هرمیتی دارای بردارهای ویژه متعامد برای مقادیر ویژه مختلف است. و این نوع ماتریس ها همیشه دارای یک مبنای متعارف از $\mathbb{C}^ n$ بردارهای ویژه ماتریس هستند.

هر ماتریس متقارن حقیقی نیز هرمیتی است. به عنوان مثال ماتریس هویت 2×2.

یک ماتریس هرمیتی را می توان به صورت مجموع یک ماتریس متقارن حقیقی به اضافه یک ماتریس موهومی متقارن بیان کرد .

A = B + Ci

جمع (یا تفریق) دو ماتریس هرمیتی برابر با ماتریس هرمیتی دیگری است، زیرا:

$(A\pm B)^H = A^H\pm B^H = A \pm B$

حاصل حاصل ضرب یک ماتریس هرمیتی و یک اسکالر در صورتی که عدد اسکالر یک عدد حقیقی باشد، ماتریس هرمیتی دیگری را ایجاد می کند.

$(k \cdot A)^H = \overline{k}\cdot A^H = k \cdot A$

حاصل ضرب دو ماتریس هرمیتی به طور کلی دوباره هرمیتی نیست. با این حال، زمانی که دو ماتریس جابجا شوند، حاصل ضرب هرمیتی است، به عبارت دیگر، نتیجه ضرب هر دو ماتریس بدون توجه به ترتیب ضرب آنها یکسان است، زیرا شرط زیر برآورده می شود:

$(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B$

اگر یک ماتریس هرمیتی یک ماتریس غیر منفرد باشد ، معکوس این ماتریس نیز یک ماتریس هرمیتی است.

$(A^{-1})^H = (A^H)^{-1} = A^{-1}$

دترمینان یک ماتریس هرمیتی همیشه معادل یک عدد حقیقی است. در اینجا اثبات این خاصیت است:

$det(A) = det(A^T) \\longrightarrow \ det(A^H) = \overline{det(A)}$

بنابراین، اگر A=A^H :

$det(A) = \overline{det(A)}$

بنابراین، برای تحقق این شرط، لزوماً الزامی است که دترمینان یک ماتریس هرمیتی باید یک عدد حقیقی باشد. بنابراین، مزدوج نتیجه با خود نتیجه برابر است.

فرمول ماتریس هرمیتی

ماتریس های هرمیتی فرمولی بسیار آسان برای به خاطر سپردن دارند: آنها با اعداد حقیقی روی قطر اصلی تشکیل می شوند و عنصر مختلط واقع در ردیف i و ستون j باید مزدوج مختلط عنصری باشد که در آن قرار دارد. j- سطر و ستون i.

در اینجا چندین مثال از کاربرد فرمول ماتریس هرمیتی آورده شده است:

ماتریس هرمیتین مرتبه 2

$\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}$

ماتریس هرمیتین مرتبه 3

$\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}$

ماتریس هرمیتین مرتبه 4

$\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}$

تجزیه یک ماتریس مختلط به یک ماتریس هرمیتی و یک ماتریس کج-هرمیتی

هر ماتریس با عناصر مختلط را می توان به مجموع یک ماتریس هرمیتی به اضافه یک ماتریس شیبدار هرمیتی دیگر تجزیه کرد . اما برای انجام این کار باید ویژگی های زیر را در این نوع ماتریس ها بدانیم:

مجموع یک ماتریس مختلط مربع به اضافه جابجایی مزدوج آن منجر به یک ماتریس هرمیتی می شود.

$C + C^H = \text{ماتریس هرمیتین}$

تفاوت بین یک ماتریس مختلط مربعی و جابه‌جایی مزدوج آن منجر به یک ماتریس کج-هرمیتی می‌شود.

$C - C^H= \text{ماتریس Skew-Hermitian}$

بنابراین، تمام ماتریس های مختلط را می توان به مجموع یک ماتریس هرمیت و یک ماتریس کج-هرمیتی تجزیه کرد. این قضیه به تجزیه تئوپلیتز معروف است :

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^H) \qquad B = \cfrac{1}{2 } \cdot (CC^H)\end{آرایه}$

در جایی که C ماتریس مختلطی است که می‌خواهیم تجزیه کنیم، C H جابه‌جایی مزدوج آن، و در نهایت A و B به ترتیب ماتریس‌های هرمیتین و ماتریس هرمیتی اریب هستند که ماتریس C به آن تجزیه می‌شود.

منبع

https://www.algebrapracticeproblems.com/hermitian-self-adjoint-matrix/

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی

ماتریس هرمیتین یا خود الحاقی

ماتریس هرمیتین یا خود الحاقی

ماتریس هرمیتین (یا خود الحاقی) چیست؟

نمونه هایی از ماتریس های هرمیتی

خواص ماتریس هرمیت

فرمول ماتریس هرمیتی

تجزیه یک ماتریس مختلط به یک ماتریس هرمیتی و یک ماتریس کج-هرمیتی

مشخصات وب

موضوعات وب

پیوندها

پیوندهای روزانه

آرشیو وب

آمارگیر وبلاگ

کد پربازدیدترین