1-مقادیر ویژه و بردارهای ویژه

توسط علی رضا نقش نیلچی | سه شنبه بیستم آذر ۱۴۰۳ | 20:57

از ویکی پدیا، دانشنامه آزاد

"ریشه مشخصه" به اینجا هدایت می شود. برای ریشه یک معادله مشخصه، به معادله مشخصه (حساب حساب) مراجعه کنید .

در جبر خطی ، بردار ویژه ( / ˈ aɪ ɡ ən -/ EYE -gən- ) یا بردار مشخصه ، برداری است که جهت آن با یک تبدیل خطی مشخص تغییر نکرده (یا معکوس شده است) . به طور دقیق تر، یک بردار ویژه،v $\mathbf {v}$ ، یک تبدیل خطی، $T$ ، با یک عامل ثابت مقیاس بندی می شود ، $\lambda$ ، هنگامی که تبدیل خطی به آن اعمال می شود: $T\mathbf {v} =\lambda \mathbf {v}$ . مقدار ویژه مربوطه ، مقدار مشخصه یا ریشه مشخصه عامل ضرب است $\lambda$ (احتمالا منفی).

از نظر هندسی، بردارها کمیت های چند بعدی با قدر و جهت هستند که اغلب به صورت فلش نشان داده می شوند. یک تبدیل خطی بردارهایی را که بر آنها اثر می‌گذارد می‌چرخاند ، کشیده یا برش می‌دهد . بردارهای ویژه آن بردارهایی هستند که فقط کشیده می شوند و نه چرخش دارند و نه برش. مقدار ویژه مربوطه عاملی است که توسط آن بردار ویژه کشیده یا فشرده می شود. اگر مقدار ویژه منفی باشد، جهت بردار ویژه معکوس می شود. [ 1 ]

بردارهای ویژه و مقادیر ویژه یک تبدیل خطی برای مشخص کردن آن استفاده می‌کنند، و بنابراین نقش مهمی در همه مناطقی که جبر خطی در آن اعمال می‌شود، از زمین‌شناسی گرفته تا مکانیک کوانتومی ، ایفا می‌کنند . به طور خاص، اغلب اتفاق می افتد که یک سیستم با یک تبدیل خطی نشان داده می شود که خروجی های آن به عنوان ورودی به همان تبدیل تغذیه می شوند ( بازخورد ). در چنین برنامه‌ای، بزرگترین مقدار ویژه از اهمیت ویژه‌ای برخوردار است، زیرا بر رفتار بلندمدت سیستم پس از بسیاری از کاربردهای تبدیل خطی حاکم است و بردار ویژه مرتبط، حالت پایدار سیستم است.

تعریف

[ ویرایش ]

یک را در نظر بگیرید $n{\times }n$ ماتریس A و یک بردار غیر صفر $\mathbf {v}$ از طول. $n.$ اگر A را در ضرب کنیم $\mathbf {v}$ (مشخص شده باv $A\mathbf {v}$ ) به سادگی ترازو $\mathbf {v}$ با ضریب λ ، که در آن λ یک اسکالر است ، پس $\mathbf {v}$ بردار ویژه A نامیده می شود و λ مقدار ویژه مربوطه است. این رابطه را می توان به صورت زیر بیان کرد: $A\mathbf {v} =\lambda \mathbf {v}$ . [ 2 ]

مطابقت مستقیمی بین n - در - n ماتریس مربع و تبدیل‌های خطی از یک فضای برداری n بعدی به خودش، با توجه به هر مبنایی از فضای برداری وجود دارد. از این رو، در یک فضای برداری با ابعاد محدود، معادل تعریف مقادیر ویژه و بردارهای ویژه با استفاده از زبان ماتریس ها یا زبان تبدیل های خطی است. [ 3 ] [ 4 ]

بخش زیر دیدگاه کلی تری را ارائه می دهد که فضاهای برداری بی بعدی را نیز پوشش می دهد .

نمای کلی

[ ویرایش ]

مقادیر ویژه و بردارهای ویژه در تجزیه و تحلیل تبدیل های خطی برجسته هستند. پیشوند eigen- از کلمه آلمانی eigen ( همزاد با کلمه انگلیسی own ) برای «مناسب»، «ویژگی»، «خود» گرفته شده است. [ 5 ] [ 6 ] در اصل برای مطالعه محورهای اصلی حرکت چرخشی اجسام صلب ، مقادیر ویژه و بردارهای ویژه کاربردهای گسترده ای دارند، به عنوان مثال در تجزیه و تحلیل پایداری ، تجزیه و تحلیل ارتعاش ، اوربیتال های اتمی ، تشخیص چهره ، و قطری ماتریس .

در اصل، یک بردار ویژه v یک تبدیل خطی T یک بردار غیر صفر است که وقتی T روی آن اعمال شود، تغییر جهت نمی دهد. اعمال T بر بردار ویژه تنها بردار ویژه را با مقدار اسکالر λ که یک مقدار ویژه نامیده می شود، مقیاس می کند. این شرط را می توان به صورت معادله نوشتتی(v)=λv، $T(\mathbf {v} )=\lambda \mathbf {v}،$ به عنوان معادله ارزش ویژه یا معادله ویژه شناخته می شود . به طور کلی، λ ممکن است هر اسکالر باشد . برای مثال، λ ممکن است منفی باشد، در این صورت بردار ویژه به عنوان بخشی از مقیاس بندی جهت معکوس می کند، یا ممکن است صفر یا مختلط باشد .

در این نگاشت برشی، فلش قرمز تغییر جهت می دهد، اما فلش آبی تغییر نمی کند. فلش آبی بردار ویژه این نگاشت برشی است زیرا جهت آن را تغییر نمی دهد و از آنجایی که طول آن بدون تغییر است، مقدار ویژه آن 1 است.

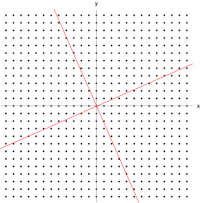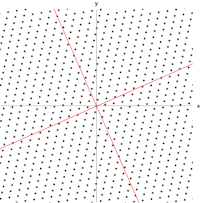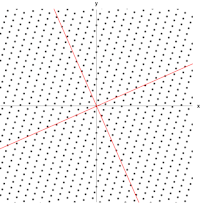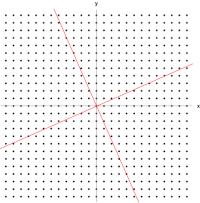
یک ماتریس حقیقی و متقارن 2×2 که نشان دهنده کشش و برش صفحه است. بردارهای ویژه ماتریس (خطوط قرمز) دو جهت خاص هستند به طوری که هر نقطه روی آنها فقط روی آنها می لغزد.

مثال در اینجا، بر اساس مونالیزا ، یک تصویر ساده ارائه می دهد. هر نقطه روی نقاشی را می توان به عنوان یک بردار نشان داد که از مرکز نقاشی به آن نقطه اشاره می کند. تبدیل خطی در این مثال نگاشت برشی نامیده می شود . نقاط در نیمه بالایی به سمت راست و نقاط نیمه پایینی به سمت چپ منتقل می شوند، متناسب با فاصله آنها از محور افقی که از وسط نقاشی می گذرد. بنابراین، بردارهایی که به هر نقطه در تصویر اصلی اشاره می‌کنند، به راست یا چپ متمایل می‌شوند و با تبدیل طولانی‌تر یا کوتاه‌تر می‌شوند. هنگام اعمال این تبدیل، نقاط در امتداد محور افقی اصلاً حرکت نمی کنند. بنابراین، هر بردار که مستقیماً به راست یا چپ و بدون مولفه عمودی اشاره می کند، بردار ویژه این تبدیل است، زیرا نگاشت جهت آن را تغییر نمی دهد. علاوه بر این، این بردارهای ویژه همگی دارای مقدار ویژه برابر با یک هستند، زیرا نگاشت طول آنها را نیز تغییر نمی دهد.

تبدیل های خطی می توانند اشکال مختلفی داشته باشند، بردارها را در فضاهای برداری مختلف نگاشت می کنند، بنابراین بردارهای ویژه نیز می توانند اشکال مختلفی داشته باشند. برای مثال، تبدیل خطی می تواند یک عملگر دیفرانسیل باشددد ${\tfrac {d}{dx}}$ ، در این صورت بردارهای ویژه توابعی هستند به نام توابع ویژه که توسط آن عملگر دیفرانسیل مقیاس بندی می شوند، ماننددد. ${\frac {d}{dx}}e^{\lambda x}=\lambda e^{\lambda x}.$ از طرف دیگر، تبدیل خطی می تواند به شکل یک ماتریس n در n باشد ، در این صورت بردارهای ویژه n در 1 ماتریس هستند. اگر تبدیل خطی به شکل n با n ماتریس A بیان شود ، معادله مقدار ویژه برای تبدیل خطی بالا می تواند به صورت ضرب ماتریس بازنویسی شود.، $A\mathbf {v} =\lambda \mathbf {v}،$ که در آن بردار ویژه v یک ماتریس n در 1 است. برای یک ماتریس، مقادیر ویژه و بردارهای ویژه را می توان برای تجزیه ماتریس استفاده کرد - برای مثال با قطری کردن آن.

مقادیر ویژه و بردارهای ویژه بسیاری از مفاهیم ریاضی مرتبط را به وجود می آورند و پیشوند eigen- به طور آزادانه هنگام نامگذاری آنها به کار می رود:

مجموعه تمام بردارهای ویژه یک تبدیل خطی، که هر کدام با مقدار ویژه متناظر خود جفت شده اند، سیستم ویژه آن تبدیل نامیده می شود. [ 7 ] [ 8 ]
مجموعه تمام بردارهای ویژه T مربوط به مقدار ویژه یکسان، همراه با بردار صفر، یک فضای ویژه یا فضای مشخصه T مرتبط با آن مقدار ویژه نامیده می شود. [ 9 ]
اگر مجموعه ای از بردارهای ویژه T پایه دامنه T را تشکیل دهد ، آنگاه به این مبنا ، پایه ویژه می گویند .

تاریخچه

[ ویرایش ]

مقادیر ویژه اغلب در زمینه جبر خطی یا نظریه ماتریس معرفی می شوند . با این حال، از نظر تاریخی، آنها در مطالعه اشکال درجه دوم و معادلات دیفرانسیل به وجود آمدند .

در قرن هجدهم، لئونارد اویلر حرکت چرخشی یک جسم صلب را مطالعه کرد و اهمیت محورهای اصلی را کشف کرد . [ a ] جوزف-لوئیس لاگرانژ متوجه شد که محورهای اصلی بردارهای ویژه ماتریس اینرسی هستند. [ 10 ]

در اوایل قرن نوزدهم، آگوستین-لوئی کوشی دید که چگونه می توان از کار آنها برای طبقه بندی سطوح چهارگانه استفاده کرد و آن را به ابعاد دلخواه تعمیم داد. [ 11 ] کوشی همچنین اصطلاح racine caractéristique (ریشه مشخصه) را برای چیزی که امروزه ارزش ویژه نامیده می شود ابداع کرد . اصطلاح او در معادله مشخصه باقی می ماند . [ ب ]

بعدها، جوزف فوریه از کار لاگرانژ و پیر سیمون لاپلاس برای حل معادله گرما با جداسازی متغیرها در رساله خود در سال 1822 با عنوان نظریه تحلیلی گرما (Théorie analytique de la chaleur) استفاده کرد . [ 12 ] چارلز فرانسوا استورم ایده های فوریه را بیشتر توضیح داد و آنها را مورد توجه کوشی قرار داد که آنها را با ایده های خود ترکیب کرد و به این حقیقیت رسید که ماتریس های متقارن حقیقی دارای مقادیر ویژه حقیقی هستند. [ 11 ] این توسط چارلز هرمیت در سال 1855 به آنچه امروزه ماتریس های هرمیتی نامیده می شود گسترش یافت . [ 13 ]

تقریباً در همان زمان، فرانچسکو بریوسکی ثابت کرد که مقادیر ویژه ماتریس‌های متعامد روی دایره واحد قرار دارند ، [ 11 ] و آلفرد کلبش نتیجه مربوطه را برای ماتریس‌های کج متقارن یافت . [ 13 ] سرانجام، کارل وایرشتراس جنبه مهمی را در نظریه پایداری که توسط لاپلاس آغاز شد، با درک اینکه ماتریس های معیوب می توانند باعث بی ثباتی شوند، روشن کرد. [ 11 ]

در این بین، جوزف لیوویل مسائل مربوط به مقدار ویژه را مشابه مسائل Sturm مطالعه کرد. رشته‌ای که در نتیجه کار آنها رشد کرد، اکنون نظریه استورم-لیویل نامیده می‌شود . [ 14 ] شوارتز اولین ارزش ویژه معادله لاپلاس را در حوزه های عمومی در اواخر قرن 19 مطالعه کرد، در حالی که پوانکاره معادله پواسون را چند سال بعد مطالعه کرد . [ 15 ]

در آغاز قرن بیستم، دیوید هیلبرت با مشاهده عملگرها به عنوان ماتریس های بی نهایت، مقادیر ویژه عملگرهای انتگرال را مطالعه کرد. [ 16 ] او اولین کسی بود که در سال 1904 از کلمه آلمانی eigen که به معنای "خود" است، [ 6 ] برای نشان دادن مقادیر ویژه و بردارهای ویژه استفاده کرد، [ c ] اگرچه ممکن است از کاربرد مرتبط هرمان فون هلمهولتز پیروی کرده باشد . برای مدتی، اصطلاح استاندارد در انگلیسی "ارزش مناسب" بود، اما اصطلاح متمایزتر "ارزش ویژه" استاندارد امروزی است. [ 17 ]

اولین الگوریتم عددی برای محاسبه مقادیر ویژه و بردارهای ویژه در سال 1929 ظاهر شد، زمانی که ریچارد فون میزس روش توان را منتشر کرد . یکی از محبوب ترین روش های امروزی، الگوریتم QR ، به طور مستقل توسط جان جی اف فرانسیس [ 18 ] و ورا کوبلانوفسکایا [ 19 ] در سال 1961 ارائه شد . [ 20 ] [ 21 ]

مقادیر ویژه و بردارهای ویژه ماتریس ها

[ ویرایش ]

همچنین ببینید: بردار اقلیدسی و ماتریس (ریاضیات)

مقادیر ویژه و بردارهای ویژه اغلب در چارچوب دروس جبر خطی متمرکز بر ماتریس ها به دانش آموزان معرفی می شوند. [ 22 ] [ 23 ] علاوه بر این، تبدیل‌های خطی در یک فضای برداری با ابعاد محدود را می‌توان با استفاده از ماتریس‌ها نشان داد، [ 3 ] [ 4 ] که به ویژه در کاربردهای عددی و محاسباتی رایج است. [ 24 ]

ماتریس A با کشش بردار x عمل می کند و جهت آن را تغییر نمی دهد، بنابراین x بردار ویژه A است .

n بردار بعدی را در نظر بگیرید که به صورت لیستی از n عدد اسکالر تشکیل شده اند، مانند بردارهای سه بعدی.. $\mathbf {x} ={\begin{bmatrix}1\\-3\\4\end{bmatrix}}\quad {\mbox{and}}\quad \mathbf {y} ={\begin{ bmatrix}-20\\60\\-80\end{bmatrix}}.$

به این بردارها مضربهای اسکالر یکدیگر، یا موازی یا هم خطی گفته می شود ، اگر λ اسکالر وجود داشته باشد به طوری که. $\mathbf {x} =\lambda \mathbf {y}.$

در این مورد، $\lambda =-{\frac {1}{20}}$ .

اکنون تبدیل خطی بردارهای n بعدی تعریف شده توسط n به n ماتریس A را در نظر بگیرید ،v=w، $A\mathbf {v} =\mathbf {w}،$ ${\begin{bmatrix}A_{11}&A_{12}&\cdots &A_{1n}\\A_{21}&A_{22}&\cdots &A_{2n}\\\vdots &\vdots &\ ddots &\vdots \\A_{n1}&A_{n2}&\cdots &A_{nn}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}={\ begin{bmatrix }w_{1}\\w_{2}\\\vdots \\w_{n}\end{bmatrix}}$ جایی که برای هر ردیف

$w_{i}=A_{i1}v_{1}+A_{i2}v_{2}+\cdots +A_{in}v_{n}=\sum _{j=1}^{n} A_{ij}v_{j}.$

اگر اتفاق بیفتد که v و w مضرب اسکالر هستند، این اگر باشد

$A\mathbf {v} =\mathbf {w} =\lambda \mathbf {v}،$ ( 1 )

سپس v یک بردار ویژه تبدیل خطی A است و ضریب مقیاس λ مقدار ویژه مربوط به آن بردار ویژه است . معادله ( 1 ) معادله مقدار ویژه برای ماتریس A است .

معادله ( 1 ) را می توان به صورت معادل بیان کرد

$\left(A-\lambda I\right)\mathbf {v} =\mathbf {0} ,$ ( 2 )

که در آن I ماتریس هویت n در n و 0 بردار صفر است.

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی