10. ردیابی ماتریس های مستطیلی
ما دیده ایم که اصول Extremum Ky Fan ردپای ماتریس های متقارن Rayleigh Quotient را به حداکثر می رساند و به حداقل می رساند. در این بخش نتایج آنالوگ از نظر ماتریس مستطیل آورده ایم. برای این منظور ردیابی یک ![]() ماتریس مستطیلی را به صورت زیر تعریف می کنیم
ماتریس مستطیلی را به صورت زیر تعریف می کنیم
 (10.1)
(10.1)
که در آن  . با این تعریف موجود مشکلات جدید برای حل وجود دارد
. با این تعریف موجود مشکلات جدید برای حل وجود دارد
 (10.2)
(10.2)
و
 (10.3)
(10.3)
با استفاده از (2.10) می بینیم که

و
 (10.4)
(10.4)
از طرف دیگر ، ماتریس ها ![]() و
و ![]() حل کننده ها (8.1) را برآورده می کنند
حل کننده ها (8.1) را برآورده می کنند
 (10.5)
(10.5)
و
 (10.6)
(10.6)
که منجر به نتیجه گیری زیر می شود.
نتیجه گیری 35 ماتریس ![]() و
و ![]() حل (10.2)
حل (10.2)
دادن مقدار بهینه از ![]() . به این معنا که،
. به این معنا که،
 (10.7)
(10.7)
نتیجه 36 ماتریس ها ![]() و
و ![]() (یا
(یا ![]() و
و
![]() ) حل (10.3) با دادن مقدار بهینه از
) حل (10.3) با دادن مقدار بهینه از  .
.
به این معنا که
 (10.8)
(10.8)
سرانجام توجه داریم که وقتی  ماتریس
ماتریس  به یک ماتریس مربع تبدیل می شود و نتیجه گیری 35 به نتیجه شناخته شده زیر کاهش می یابد.
به یک ماتریس مربع تبدیل می شود و نتیجه گیری 35 به نتیجه شناخته شده زیر کاهش می یابد.
 (10.9)
(10.9)
به عنوان مثال ، [17 ، ص. 195] ، [22 ، ص. 515 ~] ، [ 24 ].
11. محصولات مقادیر ویژه در برابر محصولات با ارزشهای واحد
کی فن از اصول افراطی خود استفاده کرده است (نتیجه 22) برای بدست آوردن نتایج آنالوگ در تعیین ماتریس های نیمه نهایی مثبت Rayleigh Quotient (به زیر مراجعه کنید). در این بخش از اصل جدید (قضیه 32) برای گسترش این نتایج به ماتریس های متعامد ضریب استفاده شده است. علاقه به این مشکلات از ویژگی های زیر ماتریس های متقارن ناشی می شود. بگذارید G یک ![]() ماتریس نیمه نهایی مثبت و متقارن با مقادیر ویژه باشد
ماتریس نیمه نهایی مثبت و متقارن با مقادیر ویژه باشد

اجازه دهید  یک
یک ![]() ماتریس دلخواه با ستونهای متعادل باشد ، و اجازه دهید
ماتریس دلخواه با ستونهای متعادل باشد ، و اجازه دهید

مقادیر ویژه ![]() ماتریس را نشان می دهد
ماتریس را نشان می دهد  . سپس ، به وضوح ،
. سپس ، به وضوح ،
 (11.1)
(11.1)
در حالی که نتیجه گیری 21 حاکی از نابرابری ها است
 (11.2)
(11.2)
اجازه دهید که ماتریس ![]() و
و ![]() به عنوان نتیجه در 22. تعریف سپس مقادیر ویژه ماتریس
به عنوان نتیجه در 22. تعریف سپس مقادیر ویژه ماتریس ![]() و
و  هستند
هستند

به ترتیب. از این رو (11.2) می بینیم که
 (11.3)
(11.3)
و
 (11.4)
(11.4)
که در آن ارزش های مطلوب برای ماتریس به دست آمده ![]() و
و ![]() ، به ترتیب. تقویت بیشتر (11.4) با استفاده از قضیه تعیین کننده هادامارد بدست می آید ، که می گوید تعیین کننده یک ماتریس نیمه نهایی مثبت متقارن
، به ترتیب. تقویت بیشتر (11.4) با استفاده از قضیه تعیین کننده هادامارد بدست می آید ، که می گوید تعیین کننده یک ماتریس نیمه نهایی مثبت متقارن  ، کوچکتر از محصول ورودی های مورب آن است. به این معنا که،
، کوچکتر از محصول ورودی های مورب آن است. به این معنا که،
 (11.5)
(11.5)
جایی که ![]() ستون j را نشان می دهد
ستون j را نشان می دهد ![]() . ترکیب (11.5) با (11.1) و (11.2) نابرابری می دهد
. ترکیب (11.5) با (11.1) و (11.2) نابرابری می دهد
 (11.6)
(11.6)
برای هر ماتریس  . همچنین ، همانطور که دیدیم ، برابری چه زمانی (11.6) برقرار است
. همچنین ، همانطور که دیدیم ، برابری چه زمانی (11.6) برقرار است  . این ما را به مشاهده زیر از Ky Fan می رساند [ 12 ].
. این ما را به مشاهده زیر از Ky Fan می رساند [ 12 ].
قضیه 37 (Ky Fan)
 (11.7)
(11.7)
و مقدار بهینه برای آن بدست می آید ![]() .
. ![]()
بیایید اکنون برگردیم تا ماتریس های ضریب مستطیلی مستطیلی را در نظر بگیریم. با استفاده از نمادهای بخش 8 ، مشکلاتی که می خواهیم حل کنیم
 (11.8)
(11.8)
و
 (11.9)
(11.9)
(مقایسه با (8.1) و (8.2) بود.) اجازه دهید ماتریس ![]() و
و ![]() به عنوان در قضیه 26. تعریف با استفاده از (2.1) یکی توانید بررسی کنید که
به عنوان در قضیه 26. تعریف با استفاده از (2.1) یکی توانید بررسی کنید که  ، است که ارزش حداکثر پاسخ ممکن، و (8.7). این ما را به نتیجه گیری زیر می رساند.
، است که ارزش حداکثر پاسخ ممکن، و (8.7). این ما را به نتیجه گیری زیر می رساند.
قضیه 38
 (11.10)
(11.10)
و مقدار بهینه برای ![]() و بدست می آید
و بدست می آید ![]() .
. ![]()
نتیجه گیری 39 اگر  آنگاه باشد
آنگاه باشد
 (11.11)
(11.11)
در کجا ![]() و
و ![]() در (2.7) تعریف شده است.
در (2.7) تعریف شده است. ![]()
راه حل (11.9) با پیروی از نکات و اثبات قضیه 29 پیدا می شود.
قضیه 40 ماتریس ها ![]() و
و ![]() حل (11.9). تعداد مقادیر منفرد مثبت ماتریس
حل (11.9). تعداد مقادیر منفرد مثبت ماتریس  است
است  . اگر
. اگر ![]() پس
پس
 (11.12)
(11.12)
در غیر این صورت ![]() ،
،
 (11.13)
(11.13)
![]()
به یاد بیاورید که ![]() . از این رو برابری
. از این رو برابری ![]() فقط در مواقعی امکان پذیر است که r = n باشد. اگر
فقط در مواقعی امکان پذیر است که r = n باشد. اگر ![]() در این صورت برابرها
در این صورت برابرها ![]() و r = n دلالت دارند
و r = n دلالت دارند  و
و  . در غیر این صورت ، وقتی
. در غیر این صورت ، وقتی  ، برابری
، برابری ![]() حاکی از آن است که
حاکی از آن است که  یا
یا ![]() .
.
نتیجه گیری 41 اگر ![]() آنگاه
آنگاه
 (11.14)
(11.14)
12. سخنان جمع بندی
طبق یک گفته قدیمی ، کل اوقات می تواند خیلی بیشتر از مجموع قطعات آن باشد. رویه ریلی-ریتز ، قضیه اكارت-یانگ و اصل حداكثر Ky Fan نتایج اساسی هستند كه چندین كاربرد دارند. مشاهده اینکه این موضوعات با هم ارتباط نزدیک دارند جدید و تعجب آور است. این مسائل را در پرتو جدید روشن می کند.
اصل حداکثر توسعه یافته ابزاری قدرتمند است که پیامدهای مهمی دارد. به طور خاص می بینیم که هم حداکثر مشکل اكارت-یانگ و هم حداكثر مسئله Ky Fan موارد خاصی از این مشاهده هستند. قضیه حداقل حداکثر ، مسئله حداکثر گسترده را با مسئله حداقل هنجار میرسکی متصل می کند.
Achiya Dax این بررسی نگاهی دوم به نتایج Ky Fan می دهد که مقادیر ویژه ماتریس های متقارن Rayleigh Quitient را در نظر می گیرند. این نتایج را به نسخه های "مستطیل شکل" که مقادیر منفرد ماتریس های ضرایب متعامد را در نظر می گیرند ، گسترش می دهد. اثبات ها سودمندی قضیه سلطه Ky Fan را نشان می دهد. با استفاده از این قضیه قضیه میرسکی به راحتی از قضیه ویل استخراج می شود. به همین ترتیب ، به ایجاد اصل افراط و تفریط گسترده کمک می کند.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
9. حداقل و حداکثر برابری
برابری ضرایب متعامد (6.1) مسئله حداقل Eckart-Young را با یک مسئله حداکثر معادل متصل می کند. اعتبار این برابری به خصوصیات خاص هنجار ماتریس Frobenius بستگی دارد. س raisedالی که در این بخش مطرح شده این است که آیا امکان گسترش این برابری به سایر هنجارهای ماتریس یکنواخت ثابت نیز وجود دارد؟ به عبارت دیگر ، مسئله حداقل هنجار میرسکی (22/4) مربوط به مسئله حداکثر هنجار (18/8) است. قضیه های بعدی در هنگام استفاده از Shatten -norm ![]() (2.16) در شکل قدرت خود ، به این س answerال پاسخ می دهند ،
(2.16) در شکل قدرت خود ، به این س answerال پاسخ می دهند ،
 (9.1)
(9.1)
قضیه 33 (حداقل-حداکثر برابری) فرض کنید که  . در این حالت تابع توان (9.1) برابری را برآورده می کند
. در این حالت تابع توان (9.1) برابری را برآورده می کند
 (9.2)
(9.2)
اثبات مقدار بهینه اصطلاح به حداقل رسیده توسط قضیه 9 (قضیه میرسکی) آورده شده است ، و این مقدار برابر است  . مقدار بهینه مسئله دیگر با حداکثر اصل (8.13) تعیین می شود و این مقدار برابر است
. مقدار بهینه مسئله دیگر با حداکثر اصل (8.13) تعیین می شود و این مقدار برابر است ![]() .
. ![]()
اگر ![]() تابع توان (9.1) با هنجار ردیابی (18/2) مطابقت داشته باشد. در این حالت (9.2) نتیجه زیبا زیر را به همراه دارد.
تابع توان (9.1) با هنجار ردیابی (18/2) مطابقت داشته باشد. در این حالت (9.2) نتیجه زیبا زیر را به همراه دارد.
 (9.3)
(9.3)
ما دیده ایم که مسئله به حداقل رساندن میرسکی (22/4) و حداکثر مسئله (18/8) دارای یک ویژگی مشترک هستند: مقادیر بهینه هر دو مسئله برای ماتریس های SVD بدست می آیند ، ![]() و
و ![]() . این مشاهده ما را قادر می سازد تا حداقل حداکثر برابری را به سایر هنجارهای یکنواخت ثابت تغییر دهیم. به عنوان مثال هنجار طیفی را در نظر بگیرید (19/2). در این حالت (9.3) با جایگزین می شود
. این مشاهده ما را قادر می سازد تا حداقل حداکثر برابری را به سایر هنجارهای یکنواخت ثابت تغییر دهیم. به عنوان مثال هنجار طیفی را در نظر بگیرید (19/2). در این حالت (9.3) با جایگزین می شود
 (9.4)
(9.4)
بعداً به یاد بیاورید که ستون های jth ماتریس های SVD یک جفت بردار منفرد تشکیل می دهند که مربوط به یکدیگر است ![]() . در واقع ، این خاصیت است که برابری در (9.2) را تضمین می کند. این راه را برای نوع دیگری از برابری فاکتورهای متعامد هموار می کند.
. در واقع ، این خاصیت است که برابری در (9.2) را تضمین می کند. این راه را برای نوع دیگری از برابری فاکتورهای متعامد هموار می کند.
قضیه 34 اجازه دهید ماتریس  و
و  از جفت بردار منحصر به فرد از تشکیل
از جفت بردار منحصر به فرد از تشکیل ![]() . به این معنا که
. به این معنا که  ، و برای
، و برای  ، ستون j ام از این ماتریس را برآورده سازد:
، ستون j ام از این ماتریس را برآورده سازد:
 ، و ضریب مستطیل
، و ضریب مستطیل  یک مقدار منفرد از است
یک مقدار منفرد از است ![]() . در این حالت تابع توان (9.1) برابری را برآورده می کند
. در این حالت تابع توان (9.1) برابری را برآورده می کند
![]() (9.5)
(9.5)
اثبات این اصطلاح  شامل
شامل ![]() قدرتهایی با ارزشهای منفرد است ، در حالی که اصطلاح دیگر شامل سایر
قدرتهایی با ارزشهای منفرد است ، در حالی که اصطلاح دیگر شامل سایر ![]() قدرتها است.
قدرتها است. ![]()
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
8. به حداکثر رساندن (به حداقل رساندن) هنجارهای ماتریس فاکتورهای متعامد
بیایید برگردیم تا ماتریس های ضریب متعامد فرم را در نظر بگیریم (5.1). تعریف کردن

و اجازه دهید

مقادیر منفرد ماتریس ضرایب متعامد را نشان می دهد  . ما باید با بررسی مشکلات شروع کنیم
. ما باید با بررسی مشکلات شروع کنیم
 (8.1)
(8.1)
و
 (8.2)
(8.2)
![]() عدد مثبت مشخص کجاست ،
عدد مثبت مشخص کجاست ،  . با این حال نتایج آینده ما را قادر می سازد تا خانواده بزرگتری از توابع هدف را مدیریت کنیم. شاید جالب ترین مشکلات این نوع در هنگام
. با این حال نتایج آینده ما را قادر می سازد تا خانواده بزرگتری از توابع هدف را مدیریت کنیم. شاید جالب ترین مشکلات این نوع در هنگام ![]() و
و ![]() . در این موارد عملکرد هدف به کاهش می یابد
. در این موارد عملکرد هدف به کاهش می یابد
 (8.3)
(8.3)
و
 (8.4)
(8.4)
به ترتیب. به طور خاص ، زمان ![]() و
و  مسئله (8.1) با مسئله اكارت-یانگ (12/6) همزمان است. حل (8.1) و (8.2) براساس پسوندهای "مستطیلی" قضیه های 20 و 21 است. قضیه اول به دلیل تامپسون است [ 37 ]. ما برای اثبات روشن بودن رابطه نزدیک آن با قضیه کاوسی اینترلاس ، اثبات آن را بیان می کنیم.
مسئله (8.1) با مسئله اكارت-یانگ (12/6) همزمان است. حل (8.1) و (8.2) براساس پسوندهای "مستطیلی" قضیه های 20 و 21 است. قضیه اول به دلیل تامپسون است [ 37 ]. ما برای اثبات روشن بودن رابطه نزدیک آن با قضیه کاوسی اینترلاس ، اثبات آن را بیان می کنیم.
قضیه 23 (قضیه بینابینی کوشی مستطیلی) اجازه دهید با حذف سطرها و ستون های ![]() ماتریس
ماتریس ![]() بدست آید . یعنی ، و . تعریف کردن
بدست آید . یعنی ، و . تعریف کردن![]()
![]()
![]()
![]()



و اجازه دهید

مقادیر واحد را نشان می دهد ![]() . سپس
. سپس
![]() (8.5)
(8.5)
بعلاوه ، تعداد مقادیر مثبت منفرد ![]() از پایین به زیر محدود می شود
از پایین به زیر محدود می شود

که در آن  . در نتیجه
. در نتیجه ![]() ، و اگر
، و اگر ![]() اولین
اولین ![]() مقادیر مفرد
مقادیر مفرد ![]() مرزهای پایین را برآورده می کند
مرزهای پایین را برآورده می کند
![]() (8.6)
(8.6)
اثبات اثبات این است ![]() که
که  تعداد کلی ردیف ها و ستون های حذف شده از طریق القای روشن است. زیرا
تعداد کلی ردیف ها و ستون های حذف شده از طریق القای روشن است. زیرا ![]() دو مورد وجود دارد که باید در نظر گرفته شود. ابتدا فرض کنید که
دو مورد وجود دارد که باید در نظر گرفته شود. ابتدا فرض کنید که ![]() با حذف یک ردیف به دست می آید
با حذف یک ردیف به دست می آید ![]() . سپس با استفاده از قضیه 20 با
. سپس با استفاده از قضیه 20 با  و
و  به نتایج مورد نظر می دهد. احتمال دوم این است که
به نتایج مورد نظر می دهد. احتمال دوم این است که ![]() با حذف یک ستون از بدست می آید
با حذف یک ستون از بدست می آید ![]() . در این حالت از قضیه 20 با
. در این حالت از قضیه 20 با  و استفاده می شود
و استفاده می شود  . استدلالهای مشابه ما را قادر می سازد تا مرحله استقرا را به پایان برسانیم.
. استدلالهای مشابه ما را قادر می سازد تا مرحله استقرا را به پایان برسانیم. ![]()
مشاهده کنید که مرزها (8.5) و (8.6) "سخت" هستند به این معنا که این مرزها می توانند به عنوان برابری برآورده شوند. به عنوان مثال ، یک ماتریس مورب را در نظر بگیرید.
نتیجه گیری 24 (قضیه تفکیک مستطیلی Poincaré)![]() ماتریس را در نظر بگیرید
ماتریس را در نظر بگیرید  ، کجا
، کجا  و کجا
و کجا  . اجازه دهید
. اجازه دهید

مقادیر منفرد ![]() ، کجا را نشان می دهد
، کجا را نشان می دهد  . سپس
. سپس
![]() (8.7)
(8.7)
بعلاوه ، مشخص کنید  که r = رتبه (A)
که r = رتبه (A)  ، و
، و  . سپس
. سپس ![]() و اگر
و اگر ![]() اولین
اولین ![]() مقادیر منفرد
مقادیر منفرد ![]() مرزهای پایین را برآورده می کند
مرزهای پایین را برآورده می کند
![]() (8.8)
(8.8)
اثبات اجازه دهید ماتریس  با تکمیل ستونها بدست آید
با تکمیل ستونها بدست آید ![]() تا مبنایی متعادل باشد
تا مبنایی متعادل باشد ![]() . اجازه دهید ماتریس
. اجازه دهید ماتریس  با تکمیل ستونها بدست آید
با تکمیل ستونها بدست آید ![]() تا مبنایی متعادل باشد
تا مبنایی متعادل باشد ![]() . سپس
. سپس ![]() ماتریس
ماتریس  همان مقادیر واحد را دارد
همان مقادیر واحد را دارد ![]() ، و
، و ![]() از
از  حذف آخرین
حذف آخرین ![]() سطرها و
سطرها و ![]() ستون های آخر بدست می آید .
ستون های آخر بدست می آید .
نتیجه گیری 25 با استفاده از نمادهای قبلی ، ![]()
![]() (8.9)
(8.9)
و
 (8.10)
(8.10)
بعلاوه ، اگر ![]() آن وقت باشد
آن وقت باشد
![]() (8.11)
(8.11)
و
 (8.12)
(8.12)
نابرابری های مشابه وقتی که تابع توان  با هر تابع با ارزش واقعی دیگری که در فاصله زمانی افزایش می یابد جایگزین می شود
با هر تابع با ارزش واقعی دیگری که در فاصله زمانی افزایش می یابد جایگزین می شود  .
.
قضیه 26 (یک اصل حداکثر مستطیلی) اجازه دهید ![]() ماتریس
ماتریس  از اولین
از اولین ![]() ستونها ساخته شود
ستونها ساخته شود ![]() ، و اجازه دهید
، و اجازه دهید ![]() ماتریس
ماتریس  از
از ![]() ستونهای اول ساخته شود
ستونهای اول ساخته شود ![]() . (آن را به یاد بیاورید
. (آن را به یاد بیاورید ![]() و
و ![]() SVD را تشکیل دهید
SVD را تشکیل دهید![]() ، به (2.1) - (2.8) مراجعه کنید.) سپس این جفت ماتریس با ارائه مقدار بهینه
، به (2.1) - (2.8) مراجعه کنید.) سپس این جفت ماتریس با ارائه مقدار بهینه
![]() . به این معنا که،
. به این معنا که،
 (8.13)
(8.13)
با این حال ، ماتریس های راه حل لزوماً منحصر به فرد نیستند.
اثبات اثبات نتیجه مستقیم (8.10) و این واقعیت است که  یک
یک ![]() ماتریس مورب است که ورودی های مورب آن است
ماتریس مورب است که ورودی های مورب آن است  .
. ![]()
نتیجه گیری 27 (حداکثر اصل Ky Fan مستطیلی) حالت خاص را در نظر بگیرید که چه زمانی ![]() . در این مورد
. در این مورد
 (8.14)
(8.14)
و مقدار بهینه برای ماتریسها بدست می آید ![]() و
و ![]() .
.
نتیجه گیری 28 مورد خاص را در نظر بگیرید وقتی که ![]() . در این مورد
. در این مورد
 (8.15)
(8.15)
و مقدار بهینه برای ماتریسها بدست می آید ![]() و
و ![]() . بعلاوه ، اگر
. بعلاوه ، اگر  پس از آن (8.15) به (12/6) کاهش یابد. این یک روش جایگزین برای اثبات قضیه اكارت-یانگ است.
پس از آن (8.15) به (12/6) کاهش یابد. این یک روش جایگزین برای اثبات قضیه اكارت-یانگ است.
قضیه 29 (یک اصل حداقل مستطیلی) اجازه دهید با حذف ستون های اول ![]() ماتریس
ماتریس  بدست آید . اجازه دهید با حذف ماتریس حاصل شود
بدست آید . اجازه دهید با حذف ماتریس حاصل شود![]()
![]()
![]()
![]()
![]()
![]()
![]() ستون به روش زیر: اگر
ستون به روش زیر: اگر  پس از آن
پس از آن ![]() از اول تشکیل
از اول تشکیل ![]() ستون از
ستون از ![]() . در غیر این صورت، هنگامی که
. در غیر این صورت، هنگامی که  ، اولین
، اولین ![]() ستون از
ستون از ![]() اولین هستند
اولین هستند ![]() ستون از
ستون از ![]() ، و ستون بقیه
، و ستون بقیه ![]() آخرین می
آخرین می  ستون از
ستون از![]() . سپس ماتریس
. سپس ماتریس ![]() و
و ![]() حل مشکل حداقل (8.2). مقدار بهینه (8.2) به عدد صحیح بستگی دارد
حل مشکل حداقل (8.2). مقدار بهینه (8.2) به عدد صحیح بستگی دارد  . اگر
. اگر ![]() مقدار بهینه برابر با صفر باشد. در غیر این صورت ، چه زمانی
مقدار بهینه برابر با صفر باشد. در غیر این صورت ، چه زمانی
![]() ، مقدار بهینه برابر است
، مقدار بهینه برابر است  .
.
اثبات اجازه دهید با حذف اولین ستون های ![]() ماتریس
ماتریس ![]() از
از ![]() ماتریس هویت بدست آید . سپس، به وضوح، . به طور مشابه، تعریف می شود ماتریس به طوری که . به این معنا که،
ماتریس هویت بدست آید . سپس، به وضوح، . به طور مشابه، تعریف می شود ماتریس به طوری که . به این معنا که، ![]()
![]()
![]()

![]()
![]()

![]()
![]() با حذف ستونهای مربوطه از ماتریس هویت بدست می آید . با در دست داشتن این نشانه ها (2.1) دلالت بر برابری ها دارد
با حذف ستونهای مربوطه از ماتریس هویت بدست می آید . با در دست داشتن این نشانه ها (2.1) دلالت بر برابری ها دارد

بنابراین ماتریس  از
از ![]() طریق حذف
طریق حذف ![]() سطرها و
سطرها و ![]() ستون های مربوطه بدست می آید .
ستون های مربوطه بدست می آید .
مشاهده کنید که ورودی های غیر صفر باقیمانده  مقادیر منفرد این ماتریس هستند. همچنین توجه داشته باشید که قانون حذف سطرها و ستون ها از
مقادیر منفرد این ماتریس هستند. همچنین توجه داشته باشید که قانون حذف سطرها و ستون ها از ![]() هدف این است که اندازه ورودی های غیر صفر باقیمانده را تا حد ممکن کوچک کند: محصول
هدف این است که اندازه ورودی های غیر صفر باقیمانده را تا حد ممکن کوچک کند: محصول ![]() اولین
اولین ![]() ردیف های
ردیف های ![]() بزرگترین
بزرگترین ![]() مقادیر منفرد را حذف می کند. سپس محصول
مقادیر منفرد را حذف می کند. سپس محصول 
![]() بزرگترین مقادیر بعدی بعدی را نابود می کند . ورودی های غیر صفر باقی مانده از
بزرگترین مقادیر بعدی بعدی را نابود می کند . ورودی های غیر صفر باقی مانده از ![]() این رو کمترین ورودی هایی هستند که می توانیم بدست آوریم.
این رو کمترین ورودی هایی هستند که می توانیم بدست آوریم.  به طور واضح ، تعداد مقادیر مثبت منفرد در ، است
به طور واضح ، تعداد مقادیر مثبت منفرد در ، است  . بهینه بودن راه حل ما از (8.8) و (12.12) ناشی می شود.
. بهینه بودن راه حل ما از (8.8) و (12.12) ناشی می شود. ![]()
یکی دیگر از جفت ماتریس است که حل (8.2) است با معکوس کردن ترتیب که در آن ما سطر و ستون از حذف به دست آورد ![]() شروع با حذف اولین:
شروع با حذف اولین: ![]() ستون از
ستون از ![]() ، که شامل
، که شامل ![]() بزرگترین مقادیر منفرد. سپس
بزرگترین مقادیر منفرد. سپس ![]() ردیف های بزرگترین مقادیر
ردیف های بزرگترین مقادیر ![]() بعدی را حذف کنید
بعدی را حذف کنید ![]() .
.
نتیجه گیری 30 (حداقل اصل مستطیلی Ky Fan) مورد خاص را در نظر بگیرید که چه زمانی ![]() و
و ![]() . در این مورد
. در این مورد
 (8.16)
(8.16)
و مقدار بهینه برای ماتریسها بدست می آید ![]() و
و ![]() .
.
نتیجه گیری 31 مورد خاص را در نظر بگیرید وقتی ![]() و
و ![]() . در این مورد
. در این مورد
 (8.17)
(8.17)
و مقدار بهینه برای ماتریسها بدست می آید ![]() و
و ![]() .
.
قضیه بعدی نتایج ما را به هنجارهای خودسرانه تغییرناپذیر گسترش می دهد.
قضیه 32 اجازه دهید ![]() یک هنجار منحصر به فرد ثابت باشد
یک هنجار منحصر به فرد ثابت باشد ![]() . سپس ماتریس ها
. سپس ماتریس ها ![]() و
و ![]() ، که (8.1) را حل می کنند ، مسئله را نیز حل می کنند
، که (8.1) را حل می کنند ، مسئله را نیز حل می کنند
 (8.18)
(8.18)
به همین ترتیب ماتریس ها ![]() و
و ![]() (8.2) را حل می کنند ، همچنین مسئله را حل می کنند
(8.2) را حل می کنند ، همچنین مسئله را حل می کنند
 (8.19)
(8.19)
اثبات از (8.7) می بینیم که مقادیر منفرد توسط مقادیر اصلی بزرگ می 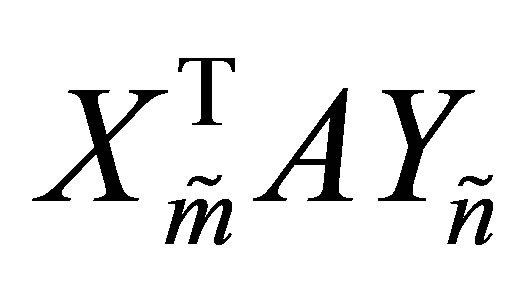 شوند
شوند  . این نشان می دهد که
. این نشان می دهد که
![]() (8.20)
(8.20)
که ادعای اول را ثابت می کند. به طور مشابه ، (8.8) به این معنی است که مقادیر منفرد توسط مقادیر مربوط  به بزرگ می شوند
به بزرگ می شوند  . این نشان می دهد که
. این نشان می دهد که
![]() (8.21)
(8.21)
که ادعای دوم را اثبات می کند. ![]()
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
7. برابری مقدارهای متقارن و اصول افراطی Ky Fan
اجازه دهید  یک
یک ![]() ماتریس متقارن واقعی با تجزیه طیفی باشد
ماتریس متقارن واقعی با تجزیه طیفی باشد
![]() (7.1)
(7.1)
که در آن  است مورب
است مورب ![]() matrixand
matrixand  متعامد
متعامد ![]() ماتریس،
ماتریس،
 . فرض بر این است که مقادیر ویژه
. فرض بر این است که مقادیر ویژه ![]() برای برآورده سازی مرتب شده اند
برای برآورده سازی مرتب شده اند
![]() (7.2)
(7.2)
اجازه دهید  یک
یک ![]() ماتریس داده شده با ستونهای متعادل و اجازه دهید
ماتریس داده شده با ستونهای متعادل و اجازه دهید

![]() ماتریس مورب را نشان می دهد که مورب را تشکیل می دهد
ماتریس مورب را نشان می دهد که مورب را تشکیل می دهد  . به یاد بیاورید
. به یاد بیاورید
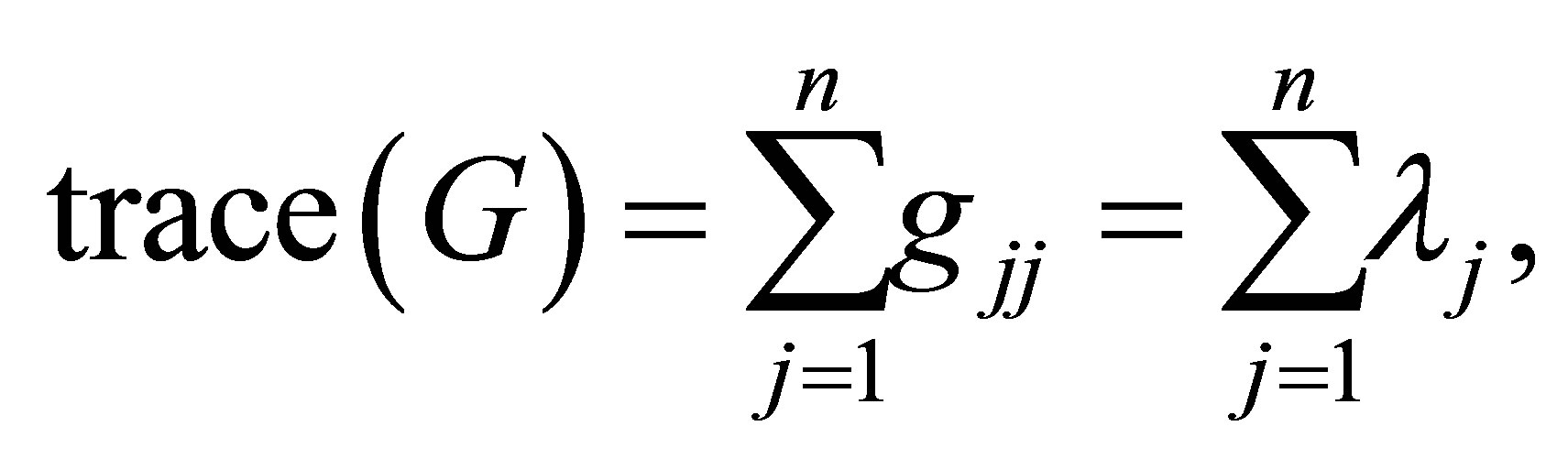
در تحولات مشابهت (متعامد) ثابت نیست. از این رو با پیروی از اثبات (6.1) نتایج زیر را بدست می آوریم.
قضیه 19 (برابری مقدارهای متقارن) با استفاده از نمادهای فوق ،
 (7.3)
(7.3)
و
 (7.4)
(7.4)
جایی که

![]()
توجه داشته باشید که قضیه 19 وقتی ![]() با هر
با هر ![]() ماتریس واقعی جایگزین شود ، معتبر باقی می ماند . نقش تقارن در مسائلی که سعی در به حداکثر رساندن یا به حداقل رساندن دارند برجسته می شود
ماتریس واقعی جایگزین شود ، معتبر باقی می ماند . نقش تقارن در مسائلی که سعی در به حداکثر رساندن یا به حداقل رساندن دارند برجسته می شود  ، همانطور که توسط کی فن در نظر گرفته شده است [ 10 ]. در یادداشت های ما ، مشکلات Ky Fan دارای شکلی است
، همانطور که توسط کی فن در نظر گرفته شده است [ 10 ]. در یادداشت های ما ، مشکلات Ky Fan دارای شکلی است
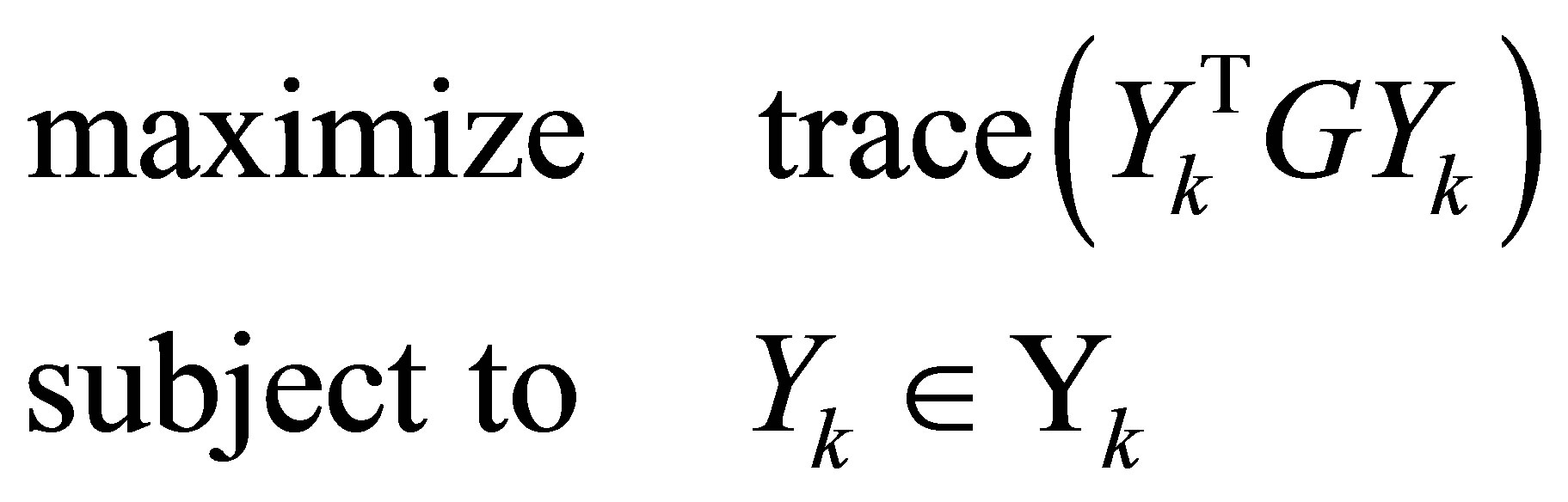 (7.5
(7.5
و
 (7.6)
(7.6)
راه حل این مشکلات در ویژگی های معروف زیر ماتریس های متقارن نهفته است ، به عنوان مثال ، [16،30،40].
قضیه 20 (قضیه بین کوشی) اجازه دهید با حذف سطرها و ستونهای مربوطه ![]() ماتریس
ماتریس ![]() بدست آید . اجازه دهید
بدست آید . اجازه دهید![]()

![]()
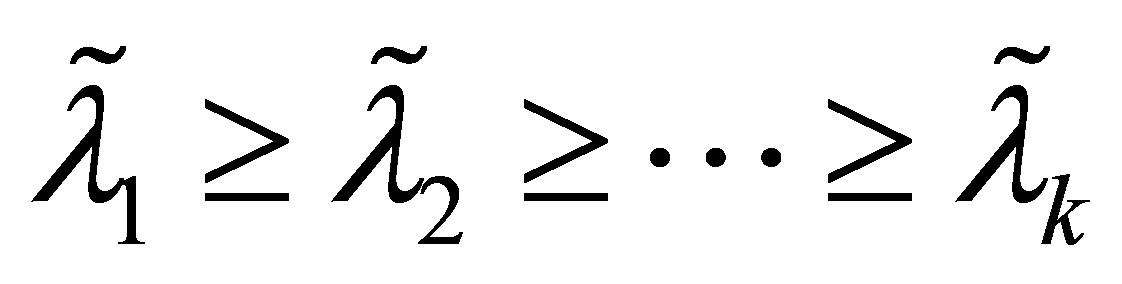
مقادیر ویژه از ![]() . سپس
. سپس
 (7.7)
(7.7)
به طور خاص  ،
،
![]() (7.8)
(7.8)
![]()
نتیجه گیری 21 (قضیه جدایی Poincaré) اجازه دهید  یک
یک ![]() ماتریس داده شده با ستونهای
ماتریس داده شده با ستونهای  متعامد طبیعی داشته باشد و یک
متعامد طبیعی داشته باشد و یک ![]() ماتریس متعامد باشد ، که
ماتریس متعامد باشد ، که ![]() ستونهای اول ستونهای آن است
ستونهای اول ستونهای آن است ![]() . سپس با حذف آخرین مورد
. سپس با حذف آخرین مورد  بدست می آید
بدست می آید 
 ردیف ها و
ردیف ها و ![]() ستون های آخر . بنابراین ، از آنجا که
ستون های آخر . بنابراین ، از آنجا که  دارای مقادیر ویژه همان مقادیر
دارای مقادیر ویژه همان مقادیر ![]() ویژه
ویژه ![]() رضایت (7.7) و (7.8) است.
رضایت (7.7) و (7.8) است.
نتیجه 22 (اصول Extremum Ky Fan) تجزیه طیفی (7.1) - (7.2) را در نظر بگیرید و اجازه دهید ماتریس  از اولین ستون های k ساخته شود
از اولین ستون های k ساخته شود ![]() . سپس
. سپس ![]() (7.5) را حل می کند ، مقدار بهینه را می دهد
(7.5) را حل می کند ، مقدار بهینه را می دهد ![]() . به این معنا که،
. به این معنا که،
 (7.9)
(7.9)
حداقل مسئله ردیابی (7.6) توسط ماتریس حل می شود

که از آخرین ![]() ستونهای تشکیل شده است
ستونهای تشکیل شده است ![]() . بنابراین ، مقدار بهینه (7.6) است
. بنابراین ، مقدار بهینه (7.6) است  . به این معنا که،
. به این معنا که،
 (7.10)
(7.10)
![]()
برابری ضرایب متقارن (7.3) به این معنی است که مشکلات Ky Fan ، (7.5) و (7.6) ، معادل مشکلات است
 (7.11)
(7.11)
و
 (7.12)
(7.12)
به ترتیب. به شباهت چشمگیر مشکلات Eckart-Young (6.8) و (6.12) و Ky Fan (7.11) و (7.5) توجه کنید.
با در نظر گرفتن موردی که G نیمه نهایی مثبت است ، بینش بیشتری به دست می آید. در این حالت تجزیه طیفی (7.1) - (7.2) با SVD همزمان می شود ![]() و
و ![]() ماتریس
ماتریس  نیز نیمه نهایی مثبت است. اجازه دهید
نیز نیمه نهایی مثبت است. اجازه دهید
![]() (7.13)
(7.13)
مقادیر ویژه (مقادیر منفرد) این ماتریس را نشان می دهد. سپس در اینجا روابط درهم آمیخته (7.7) دلالت بر روابط عمده سازی بین مقادیر واحد  و مقادیر واحد ماتریس ها دارد
و مقادیر واحد ماتریس ها دارد ![]()
و  . در نتیجه ، برای هر هنجار واحدی که ثابت باشد
. در نتیجه ، برای هر هنجار واحدی که ثابت باشد ![]() ، ماتریس
، ماتریس ![]() مسئله را حل می کند
مسئله را حل می کند
 (7.14)
(7.14)
در حالی ![]() که مشکل را حل می کند
که مشکل را حل می کند
 (7.15)
(7.15)
در بخش بعدی ما از ماتریس های ضامن متعامد متقارن به ماتریس های مستطیلی می رویم. در این حالت ارزشهای منفرد نقش مقادیر ویژه را دارند. با این حال ، همانطور که خواهیم دید ، تشبیه بین دو مورد همیشه ساده نیست.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
6. برابری امتیازات متعامد و قضیه اكارت-یانگ
در این بخش ما برابری فاکتورهای متعامد را استخراج کرده و در مورد رابطه آن با قضیه اكارت-یانگ بحث می كنیم.
قضیه 14 (برابری مقدارهای متعامد) اجازه دهید  و
و  یک جفت ماتریس مشخص با ستونهای متعادل داشته باشید. سپس
یک جفت ماتریس مشخص با ستونهای متعادل داشته باشید. سپس
![]() (6.1)
(6.1)
اثبات به دنبال اثبات قضیه 11 می بینیم که
![]() (6.2)
(6.2)
جایی که

بنابراین ، از آنجا  که زیرماتریک اصلی است
که زیرماتریک اصلی است  ،
،

نتیجه گیری 15 اجازه دهید  هر
هر ![]() ماتریسی باشد که ورودی های آن مطابق با قانون زیر باشد: یا
ماتریسی باشد که ورودی های آن مطابق با قانون زیر باشد: یا  یا
یا
![]() . به عبارت دیگر ،
. به عبارت دیگر ، ![]() از
از  صفر قرار دادن برخی از ورودی ها بدست می آید . سپس
صفر قرار دادن برخی از ورودی ها بدست می آید . سپس
![]() (6.3)
(6.3)
نتیجه 16 (متعامد خارج قسمت برابری در فرم مورب) اجازه دهید  و
و  یک جفت داده از ماتریس با ستون orthonormal. سپس ماتریس مورب (5.10) برآورده می شود
یک جفت داده از ماتریس با ستون orthonormal. سپس ماتریس مورب (5.10) برآورده می شود
![]() (6.4)
(6.4)
در نمادهای برداری آخرین برابری شکل می گیرد
 (6.5)
(6.5)
![]()
بیایید اکنون برگردیم تا مشکل Eckart-Young را بررسی کنیم (4.20). یکی از روشهای بیان ![]() ماتریس ، که رتبه آن حداکثر است
ماتریس ، که رتبه آن حداکثر است ![]() ، می باشد
، می باشد
![]() (6.6)
(6.6)
که در آن  ،
،  و
و  . متناوبا ما می توانیم
. متناوبا ما می توانیم ![]() در فرم بنویسیم
در فرم بنویسیم
 (6.7)
(6.7)
ماتریس  مورب واقعی کجاست
مورب واقعی کجاست ![]() (شکل اول از تجزیه کامل متعامد حاصل می شود
(شکل اول از تجزیه کامل متعامد حاصل می شود ![]() ، در حالی که فرم دوم از SVD حاصل می شود.) جایگزینی (6/6) در عملکرد هدف (20/4) منجر به عملکرد می شود
، در حالی که فرم دوم از SVD حاصل می شود.) جایگزینی (6/6) در عملکرد هدف (20/4) منجر به عملکرد می شود  . از این رو ، توسط قضیه 11 ، از دست دادن عمومیت در جایگزینی
. از این رو ، توسط قضیه 11 ، از دست دادن عمومیت در جایگزینی ![]() با وجود ندارد
با وجود ندارد  . به همین ترتیب D را می توان با جایگزین کرد
. به همین ترتیب D را می توان با جایگزین کرد![]() ، راه حل (5.11). این مشاهدات منجر به نتیجه گیری زیر می شود.
، راه حل (5.11). این مشاهدات منجر به نتیجه گیری زیر می شود.
قضیه 17 (فرمولهای معادل مسئله EckartYoung) در نوشتن مسئله Eckart-Young (4.20) در فرمها هیچ افت کلی وجود ندارد.
 (6.8)
(6.8)
یا
 (6.9)
(6.9)
علاوه بر این ، هر دو مشکل توسط ماتریس SVD ![]() و حل می شوند
و حل می شوند ![]() . (برای تعریف این ماتریس ها به (2.1) - (2.7) مراجعه کنید.)
. (برای تعریف این ماتریس ها به (2.1) - (2.7) مراجعه کنید.) ![]()
عملکردهای عینی آخرین مشکلات ، جناح چپ برابری فاکتورهای متعامد را تشکیل می دهد
![]() (6.10)
(6.10)
و
![]() (6.11)
(6.11)
این روابط حداقل مشکلات هنجار (8/6) - (9/6) را به حداکثر معادلات نرمال تبدیل می کند.
قضیه 18 (حداکثر فرمول بندی نرمال مسئله اكارت-یانگ) مسائل اكارت-یانگ (6.8) و (6.9) معادل مسایل است
 (6.12)
(6.12)
و
 (6.13)
(6.13)
به ترتیب. ماتریس SVD ![]() و
و ![]() حل هر دو مشکل.
حل هر دو مشکل. ![]()
بگذارید  ، مقادیر منفرد ماتریس ضرایب متعامد را نشان دهیم
، مقادیر منفرد ماتریس ضرایب متعامد را نشان دهیم  . سپس ، به وضوح ،
. سپس ، به وضوح ،
![]() (6.14)
(6.14)
و مسئله اكارت-یانگ (6.12) را می توان دوباره نوشت
 (6.15)
(6.15)
در بخشهای بعدی ، مشکلات گسترده این نوع را در نظر می گیریم. کلید حل مشکلات گسترده در خصوصیات ماتریس های ضریب متعامد متقارن نهفته است.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
5. حداقل ویژگیهای مربعات ماتریس های ضریب متعامد
خصوصیات بهینه سازی ماتریس های متقارن Rayleigh Quentient اساس روش مشهور RayleighRitz را تشکیل می دهند ، به عنوان مثال ، [30،34]. در این بخش خصوصیات مربوط به ماتریس های ضریب متعامد را بدست می آوریم. همانطور که خواهیم دید ، ماتریس های متعامد متعامد ماتریس های متقارن ریلی را به همان روشی که ضرایب مستطیل ضرایب ریلی را گسترش می دهند ، گسترش می دهند.
قضیه 11 بگذارید
 و
و 
یک جفت ماتریس مشخص با ستونهای متعادل باشد ، و اجازه دهید
![]() (5.1)
(5.1)
ماتریس ضریب متعامد مربوطه را نشان می دهد. سپس ![]() سه مشکل زیر را حل می کند.
سه مشکل زیر را حل می کند.
 (5.2)
(5.2)
 (5.3)
(5.3)
و
 (5.4)
(5.4)
اثبات تکمیل ستون ها ![]() به عنوان یک قاعده طبیعی از
به عنوان یک قاعده طبیعی از ![]() یک
یک ![]() ماتریس متعامد
ماتریس متعامد ![]() ، که اولین
، که اولین ![]() ستون های آن ستون ها است ، می دهد
ستون های آن ستون ها است ، می دهد ![]() . به طور مشابه یک
. به طور مشابه یک ![]() ماتریس متعامد وجود دارد
ماتریس متعامد وجود دارد ![]() که اولین آن است
که اولین آن است ![]() ستون ها ستون های
ستون ها ستون های ![]() . بنابراین ، از آنجا که هنجار Frobenius بطور واحدی ثابت نیست ،
. بنابراین ، از آنجا که هنجار Frobenius بطور واحدی ثابت نیست ،
 (5.5)
(5.5)
جایی که
 (5.6)
(5.6)
اعتبار آخرین برابری با ذکر این نکته که ![]() ماتریس
ماتریس  از اولین
از اولین ![]() ستون های
ستون های ![]() ماتریس هویت تشکیل شده است ، به راحتی تأیید می شود ، در حالی که
ماتریس هویت تشکیل شده است ، به راحتی تأیید می شود ، در حالی که ![]() ماتریس
ماتریس ![]() از اولین
از اولین ![]() ردیف های
ردیف های ![]() ماتریس هویت. همچنین توجه داشته باشید که زیر متغیر اصلی مربوط به
ماتریس هویت. همچنین توجه داشته باشید که زیر متغیر اصلی مربوط به  است
است  . از این رو انتخاب به
. از این رو انتخاب به  حداقل می رسد
حداقل می رسد ![]() .
.
دو مسئله دیگر با استفاده از برابری با استدلال های مشابه حل می شوند
![]() (5.7)
(5.7)
و
![]() (5.8)
(5.8)
جایی که
 (5.9)
(5.9)
![]()
تذکر بازرسی بیشتر از روابط (5.7) - (5.9) نشان می دهد که ![]() مشکلات (5.3) و (5.4) را حل می کند حتی اگر هنجار Frobenius با هر یک از هنجارهای ماتریس منحصر به فرد دیگری جایگزین شود. با این حال آخرین ادعا برای مسئله معتبر نیست (5.2) ، زیرا "مشت زدن" یک ماتریس ممکن است هنجار آن را افزایش دهد. برای دیدن این نکته ماتریس ها را در نظر بگیرید
مشکلات (5.3) و (5.4) را حل می کند حتی اگر هنجار Frobenius با هر یک از هنجارهای ماتریس منحصر به فرد دیگری جایگزین شود. با این حال آخرین ادعا برای مسئله معتبر نیست (5.2) ، زیرا "مشت زدن" یک ماتریس ممکن است هنجار آن را افزایش دهد. برای دیدن این نکته ماتریس ها را در نظر بگیرید
 و
و  هنجارهای ردیابی آنها به ترتیب 2 و
هنجارهای ردیابی آنها به ترتیب 2 و ![]() است. یعنی مشت زدن
است. یعنی مشت زدن ![]() هنجار کمیاب آن را افزایش می دهد. با این وجود ، مشت زدن به یک ماتریس همیشه هنجار Frobenius را کاهش می دهد. از این رو اثبات قضیه 11 به نتایج قدرتمند زیر منجر می شود.
هنجار کمیاب آن را افزایش می دهد. با این وجود ، مشت زدن به یک ماتریس همیشه هنجار Frobenius را کاهش می دهد. از این رو اثبات قضیه 11 به نتایج قدرتمند زیر منجر می شود.
نتیجه گیری 12 اجازه دهید ![]() مجموعه تمام
مجموعه تمام ![]() ماتریس های واقعی که الگوی صفر خاصی دارند را نشان دهیم. (به عنوان مثال ، مجموعه تمام ماتریس های سه ضلعی) اجازه دهید ماتریس
ماتریس های واقعی که الگوی صفر خاصی دارند را نشان دهیم. (به عنوان مثال ، مجموعه تمام ماتریس های سه ضلعی) اجازه دهید ماتریس  از
از  طریق تنظیم صفر در مکان های مربوطه بدست آید . سپس قضیه 11 وقتی معتبر باقی می ماند
طریق تنظیم صفر در مکان های مربوطه بدست آید . سپس قضیه 11 وقتی معتبر باقی می ماند ![]() و با
و با  آنها جایگزین می شود
آنها جایگزین می شود ![]() و
و ![]() به ترتیب
به ترتیب ![]()
نتیجه 13 فرض کنید  و اجازه دهید
و اجازه دهید

مجموعه تمام ![]() ماتریس های مورب واقعی را نشان می دهد . اجازه دهید
ماتریس های مورب واقعی را نشان می دهد . اجازه دهید  و
و  یک جفت ماتریس مشخص با ستونهای متعادل باشد. سپس ماتریس
یک جفت ماتریس مشخص با ستونهای متعادل باشد. سپس ماتریس
![]() (5.10)
(5.10)
سه مشکل زیر را حل می کند.
 (5.11)
(5.11)
 (5.12)
(5.12)
و
 (5.13)
(5.13)
![]()
همانند مورد اسکالر ، توابع باقیمانده ، ![]() و
و ![]() ما را قادر می سازد تا "فاصله" بین مقادیر منفرد
ما را قادر می سازد تا "فاصله" بین مقادیر منفرد ![]() و
و ![]() . برای لحظه ای فرض کنید
. برای لحظه ای فرض کنید  و بگذارید
و بگذارید  مقادیر واحد را نشان دهد
مقادیر واحد را نشان دهد ![]() . آنگاه یک جایگشت وجود دارد
. آنگاه یک جایگشت وجود دارد ![]() از
از  جمله که
جمله که
 (5.14)
(5.14)
رجوع شود به [2،21]. روابط (5.7) - (5.9) نشان می دهد که حداقل مقادیر برابر ![]() و
و ![]() برابر هنجار Frobenius بلوک های خارج مورب متناظر در ماتریس
برابر هنجار Frobenius بلوک های خارج مورب متناظر در ماتریس  . مشاهدات بعدی مربوط به حداقل مقدار
. مشاهدات بعدی مربوط به حداقل مقدار ![]() .
.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
4- از مقادیر ویژه تا مقادیر واحد
ارتباط بین مقادیر منفرد ![]() و مقادیر ویژه ماتریس های A T A ، AA T و
و مقادیر ویژه ماتریس های A T A ، AA T و کاملاً ساده است در واقع ، بسیاری از خصوصیات مقادیر منفرد از این اتصال به ارث می رسند. با این حال ، همانطور که بررسی ما نشان می دهد ، عمق روابط بسیار فراتر از این ارتباط اساسی است. قضیه مینیمکس Courant-Fischer و قضیه Weyl نتایج بسیار مفیدی را در مقادیر ویژه ماتریس های متقارن ارائه می دهند. برای جزئیات بحث در مورد این قضیه ها و پیامدهای آن به [1،30] مراجعه کنید. در زیر سازگاری این نتایج را هنگام حرکت از مقادیر ویژه به مقادیر واحد در نظر می گیریم. از قضیه های سازگار برای ارائه اثبات "سنتی" قضیه اكارت-یانگ استفاده می شود.
کاملاً ساده است در واقع ، بسیاری از خصوصیات مقادیر منفرد از این اتصال به ارث می رسند. با این حال ، همانطور که بررسی ما نشان می دهد ، عمق روابط بسیار فراتر از این ارتباط اساسی است. قضیه مینیمکس Courant-Fischer و قضیه Weyl نتایج بسیار مفیدی را در مقادیر ویژه ماتریس های متقارن ارائه می دهند. برای جزئیات بحث در مورد این قضیه ها و پیامدهای آن به [1،30] مراجعه کنید. در زیر سازگاری این نتایج را هنگام حرکت از مقادیر ویژه به مقادیر واحد در نظر می گیریم. از قضیه های سازگار برای ارائه اثبات "سنتی" قضیه اكارت-یانگ استفاده می شود.
مانند قبل ![]() یک
یک ![]() ماتریس واقعی را نشان می دهد که SVD آن با (2.1) - (2.7) داده شده است. جفت اول قضیه ها خصوصیات مفید "minimax" از مقادیر واحد را ارائه می دهد. در این قضایا
ماتریس واقعی را نشان می دهد که SVD آن با (2.1) - (2.7) داده شده است. جفت اول قضیه ها خصوصیات مفید "minimax" از مقادیر واحد را ارائه می دهد. در این قضایا ![]() نشانگر یک فضای خرده دلخواه از
نشانگر یک فضای خرده دلخواه از ![]() بعد است
بعد است ![]() . به طور مشابه ،
. به طور مشابه ، ![]() یک فضای خرده دلخواه از
یک فضای خرده دلخواه از ![]() بعد نشان می دهد
بعد نشان می دهد ![]() .
.
قضیه 1 (قضیه Minimax سمت راست Courant-Fischer) ارزش انحصاری jth از ![]() رضایت مندی ها
رضایت مندی ها
![]() (4.1)
(4.1)
و
 (4.2)
(4.2)
جایی که عدد صحیح ![]() با برابری تعریف می شود
با برابری تعریف می شود
![]() (4.3)
(4.3)
(حداکثر در (4.1) از همه است ![]() زیرفضاهای بعدی
زیرفضاهای بعدی ![]() از
از ![]() . حداقل در (4.2) از همه است
. حداقل در (4.2) از همه است ![]() زیرفضاهای بعدی
زیرفضاهای بعدی ![]() از
از ![]() .) علاوه بر این، حداکثر در (4.1) برای به دست آمده
.) علاوه بر این، حداکثر در (4.1) برای به دست آمده  ، در حالی که حداقل در (4.2) برای به دست آمده
، در حالی که حداقل در (4.2) برای به دست آمده
 .
.
با این حال راه حل های هر دو مشکل لزوماً منحصر به فرد نیستند. ![]()
قضیه 2 (قضیه Minimax Legend Courant-Fischer) ارزش انفرادی ![]() رضایت
رضایت
![]() (4.4)
(4.4)
و
![]() (4.5)
(4.5)
جایی که عدد صحیح ![]() با برابری تعریف می شود
با برابری تعریف می شود
![]() (4.6)
(4.6)
علاوه بر این ، حداکثر در (4.4) برای بدست آمده است
 در حالی که حداقل در (4.5) برای بدست آمده است
در حالی که حداقل در (4.5) برای بدست آمده است
 .
. ![]()
توجه داشته باشید که قضیه 2 در اصل قضیه 1 برای است ![]() . اثبات قضیه 1 بر اساس ایده زیر است. شرط (4.3) تضمین می کند وجود یک بردار واحد،
. اثبات قضیه 1 بر اساس ایده زیر است. شرط (4.3) تضمین می کند وجود یک بردار واحد، ![]() که هر دو متعلق به
که هر دو متعلق به ![]() و
و ![]() . بدین ترتیب
. بدین ترتیب

و

بنابراین اثبات با تأیید برابری هنگام استفاده از زیر فضاهای مشخص شده به نتیجه می رسد.
بگذارید ![]() یک
یک ![]() ماتریس واقعی دیگر را نشان دهیم و بگذارید
ماتریس واقعی دیگر را نشان دهیم و بگذارید
![]() (4.7)
(4.7)
ماتریس اختلاف مربوطه را نشان می دهد. مقادیر منفرد ![]() و
و ![]() به عنوان نشان داده می شوند
به عنوان نشان داده می شوند
![]() (4.8)
(4.8)
به ترتیب. نتیجه های بعدی قضیه 1 به این سوال پاسخ می دهد که چگونه رتبه ![]() بر مقادیر واحد تأثیر می گذارد
بر مقادیر واحد تأثیر می گذارد ![]() .
.
لما 3 فرض کنید که  . در این مورد
. در این مورد
![]() (4.9)
(4.9)
اثبات نگاهی  . سپس
. سپس  و
و  . در نتیجه
. در نتیجه

جایی که آخرین نابرابری از (4.2) ناشی می شود. ![]()
قضیه 4 (ویل) بگذارید ![]() و
و ![]() مانند (4.7) - (4.8) باشد. سپس
مانند (4.7) - (4.8) باشد. سپس
![]() (4.10)
(4.10)
تحت این کنوانسیون که  وقتی
وقتی ![]() .
.
اثبات بگذارید ![]() یک
یک ![]() SVD کوتاه شده از یک
SVD کوتاه شده از یک ![]() ، و
، و ![]() یک
یک ![]() SVD کوتاه شده یک درجه
SVD کوتاه شده یک درجه ![]() باشد. سپس بزرگترین مقدار مفرد از
باشد. سپس بزرگترین مقدار مفرد از  است
است ![]() ، در حالی که بزرگترین مقدار مفرد از
، در حالی که بزرگترین مقدار مفرد از  است
است ![]() . به این معنا که،
. به این معنا که،
![]() (4.11)
(4.11)
و
![]() (4.12)
(4.12)
اجازه دهید ![]() ماتریس
ماتریس ![]() با برابری تعریف شود
با برابری تعریف شود

سپس  ، و
، و

از این رو (4.11) و (4.12) می بینیم که

جایی که آخرین نابرابری از Lemma 3 ناشی می شود. ![]()
نتیجه 5 (Majorization) دوباره فرض که  ، که به معنی
، که به معنی  برای
برای  . سپس با جایگزینی
. سپس با جایگزینی  (4.10) می توانید جایگزین کنید
(4.10) می توانید جایگزین کنید
![]() (4.13)
(4.13)
به عبارت دیگر ، اگر  در این صورت مقادیر
در این صورت مقادیر ![]() منفرد مقادیر منفرد را بزرگ می کند
منفرد مقادیر منفرد را بزرگ می کند  .
. ![]()
به یاد بیاورید که ![]() نشان دهنده یک
نشان دهنده یک ![]() SVD کوتاه شده از درجه است
SVD کوتاه شده از درجه است ![]() ، همانطور که در (2.8) تعریف شده است. به طور تقریبی ، آخرین نتیجه گیری می گوید که
، همانطور که در (2.8) تعریف شده است. به طور تقریبی ، آخرین نتیجه گیری می گوید که ![]() اغتشاش در مرتبه
اغتشاش در مرتبه ![]() ممکن است باعث شود که مقادیر واحد بیش از
ممکن است باعث شود که مقادیر واحد بیش از ![]() «سطح» سقوط نکند . نتیجه بعدی نشان می دهد که آنها قادر به "افزایش" بیش از
«سطح» سقوط نکند . نتیجه بعدی نشان می دهد که آنها قادر به "افزایش" بیش از ![]() سطح نیستند.
سطح نیستند.
نتیجه 6 مشاهده کنید که (4.7) می تواند دوباره نوشته شود  در حالی که
در حالی که ![]() دارای مقادیر منفرد یکسانی است
دارای مقادیر منفرد یکسانی است ![]() . از این رو نتیجه دیگری از قضیه 4 است
. از این رو نتیجه دیگری از قضیه 4 است
![]() (4.14)
(4.14)
علاوه بر این ، اگر  آن وقت باشد
آن وقت باشد
![]() (4.15)
(4.15)
![]()
نتایج بعدی مرزهای مفیدی را در مقادیر مفرد آشفته ایجاد می کنند.
نتیجه 7 (محدوده و درهم بافته) با استفاده از (4.10) و (4.14) با ![]() می دهد
می دهد
![]() (4.16)
(4.16)
و
![]() (4.17)
(4.17)
بعلاوه ، مورد خاص را در نظر بگیرید که ![]() ماتریس رتبه یک باشد. سپس با استفاده از (4.13) و (4.15) همراه با داده
ماتریس رتبه یک باشد. سپس با استفاده از (4.13) و (4.15) همراه با داده ![]() می شود
می شود
![]() (4.18)
(4.18)
که در آن  و
و  .
. ![]()
قضیه 8 (اكارت-یانگ) بگذارید ![]() و
و ![]() مانند (4.7) - (4.8) باشد و فرض كنید كه
مانند (4.7) - (4.8) باشد و فرض كنید كه  . سپس
. سپس
 (4.19)
(4.19)
علاوه بر این ، اجازه دهید ![]() یک
یک ![]() SVD کوتاه شده از آن باشد
SVD کوتاه شده از آن باشد ![]() ، همانطور که در (2.8) تعریف شده است. سپس
، همانطور که در (2.8) تعریف شده است. سپس ![]() حداقل مسئله هنجار را حل می کند
حداقل مسئله هنجار را حل می کند
 (4.20)
(4.20)
دادن مقدار بهینه از

اثبات با استفاده از (4.13) می بینیم که

![]()
آخرین قضیه می گوید که ![]() بهترین
بهترین ![]() تقریب
تقریب ![]() رتبه در مورد هنجار Frobenius است. مشاهده کنید که Lemma 3 ادعای مشابهی برای هنجار 2 را اثبات می کند. پسوند بعدی به دلیل میرسکی است [ 23 ].
رتبه در مورد هنجار Frobenius است. مشاهده کنید که Lemma 3 ادعای مشابهی برای هنجار 2 را اثبات می کند. پسوند بعدی به دلیل میرسکی است [ 23 ].
قضیه 9 (میرسکی) اجازه دهید ![]() یک هنجار منحصر به فرد ثابت را نشان دهد
یک هنجار منحصر به فرد ثابت را نشان دهد ![]() . سپس نابرابری
. سپس نابرابری
![]() (4.21)
(4.21)
نگه می دارد برای هر ماتریس  به طوری که
به طوری که  . به عبارت دیگر ،
. به عبارت دیگر ، ![]() مسئله حداقل هنجار را حل می کند
مسئله حداقل هنجار را حل می کند
 (4.22)
(4.22)
اثبات از نتیجه 5 می بینیم که مقادیر منحصر به فرد بزرگ کردن مقادیر ![]() آن است
آن است  . از این رو (4.21) نتیجه مستقیم قضیه تسلط Ky Fan است.
. از این رو (4.21) نتیجه مستقیم قضیه تسلط Ky Fan است. ![]()
یکی دیگر از مشکلات مرتبط است
 (4.23)
(4.23)
که ![]() نشانگر مجموعه تمام
نشانگر مجموعه تمام ![]() ماتریسهای واقعی درجه است
ماتریسهای واقعی درجه است ![]() . در زیر نشان خواهیم داد که ماتریس باقیمانده
. در زیر نشان خواهیم داد که ماتریس باقیمانده
 (4.24)
(4.24)
این مشکل را حل می کند به عبارت دیگر ، ![]() کوچکترین آشفتگی است که
کوچکترین آشفتگی است که ![]() به یک
به یک ![]() ماتریس رتبه بندی تبدیل می شود .
ماتریس رتبه بندی تبدیل می شود .
قضیه 10 Let ![]() و C مانند (4.7) است و فرض کنید که
و C مانند (4.7) است و فرض کنید که

سپس
 (4.25)
(4.25)
اثبات با استفاده از قضیه اكارت-یانگ به دست می آوریم

![]()
مشاهده کنید که ![]() حل این مسئله (4.23) هنگامی که این مسئله با هر هنجار غیرقابل تغییر دیگری تعریف می شود ، باقی می ماند. همچنین توجه داشته باشید که مشکلات Total Least Squares شکل خاصی از (23/4) را ایجاد می کند که در آن
حل این مسئله (4.23) هنگامی که این مسئله با هر هنجار غیرقابل تغییر دیگری تعریف می شود ، باقی می ماند. همچنین توجه داشته باشید که مشکلات Total Least Squares شکل خاصی از (23/4) را ایجاد می کند که در آن  . در این حالت ، ماتریس محلول ، به ماتریس
. در این حالت ، ماتریس محلول ، به ماتریس ![]() رتبه یک کاهش می یابد
رتبه یک کاهش می یابد  ، به عنوان مثال ، [14،15]. عواقب بیشتر قضیه اكارت-یانگ در بخش 6 ارائه شده است.
، به عنوان مثال ، [14،15]. عواقب بیشتر قضیه اكارت-یانگ در بخش 6 ارائه شده است.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
3. ضرایب مستطیل
اجازه دهید ![]() یک
یک ![]() ماتریس واقعی با
ماتریس واقعی با  ، و اجازه دهید
، و اجازه دهید
 و
و  یک جفت بردار غیر صفر باشید. برای ساده کردن بحث های آینده ما را فرض هایی که
یک جفت بردار غیر صفر باشید. برای ساده کردن بحث های آینده ما را فرض هایی که  ، و
، و ![]() و
و ![]() بردار واحد می باشد. به این معنا که،
بردار واحد می باشد. به این معنا که،

با استفاده از این مفروضات ، مقدار مستطیل (1.6) به فرم دو خطی کاهش می یابد
![]() (3.1)
(3.1)
در این بخش ما مختصراً حداقل ویژگیهای اساسی حداقل را که مشخصه این نوع اشکال دو خطی است ، استخراج می کنیم. در ابتدا باید یادآوری کنیم که ![]() مسئله به حداقل رساندن یک پارامتر را حل می کند
مسئله به حداقل رساندن یک پارامتر را حل می کند
![]() (3.2)
(3.2)
این مشاهده نتیجه مستقیم برابری هاست


و
 (3.3)
(3.3)
استدلال های مشابه نشان می دهد که  مشکلات حداقل مربعات را حل می کند
مشکلات حداقل مربعات را حل می کند
![]() (3.4)
(3.4)
و
![]() (3.5)
(3.5)
بعلاوه ، جایگزینی مقدار بهینه مقدار ![]() (3.3) ، برابری مقدار مستطیل را به دست می دهد
(3.3) ، برابری مقدار مستطیل را به دست می دهد
![]() (3.6)
(3.6)
که به معنی حل مسئله تقریب رتبه یک است
![]() (3.7)
(3.7)
معادل حل مسئله حداکثر است
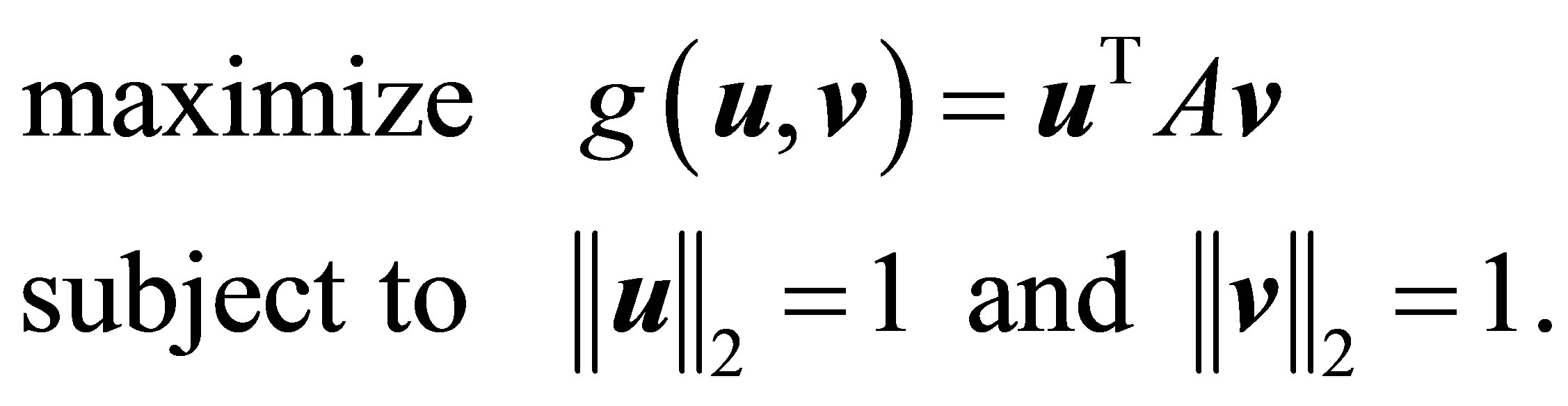 (3.8)
(3.8)
با استفاده از SVD ![]() بردارهای واحد در آخرین مسئله می توان به صورت بیان شد
بردارهای واحد در آخرین مسئله می توان به صورت بیان شد

بنابراین ، از آن زمان
![]() (3.9)
(3.9)
عملکرد هدف (3.8) را برآورده می کند

جایی که آخرین نابرابری از نابرابری کوشی شوارتز ناشی می شود. علاوه بر این ، از آنجا که  ، این جفت بردار حل می شود (3.8) ، در حالی که
، این جفت بردار حل می شود (3.8) ، در حالی که ![]() رضایت بخش است
رضایت بخش است
 (3.10)
(3.10)
آخرین نتیجه مشابه (1.4) است. با این حال ، در مقابل (1.5) ، در اینجا روابط متعامد بودن (3.9) بر این دلالت دارد
![]() (3.11)
(3.11)
خصوصیات حداقل حداکثر ضرایب مستطیل اسکالر از قضیه Courant-Fischer بدست آمده است ، به بخش بعدی مراجعه کنید.
توجیه دیگری که در پشت تعریف پیشنهادی ضریب مستطیل وجود دارد ، ناشی از مشاهده است که ضریب ریلی مربوط به ماتریس است
 و بردار
و بردار  است
است  .
.
از این رو در این مورد حد (1.2) حاکی از وجود یک مقدار منحصر به فرد از ![]() ،
، ![]() که ارضا
که ارضا
 (3.12)
(3.12)
آخرین محدوده را می توان با استفاده از قوانین بازیابی زیر ، که در [ 3 ] مشتق شده است ، اصلاح کرد . بگذارید  یک بردار واحد معین باشد که راضی کند
یک بردار واحد معین باشد که راضی کند  ، و اجازه دهید
، و اجازه دهید

و

به ترتیب برآورد مربوط به یک بردار مجرد چپ و یک مقدار واحد را ارائه دهید سپس

و (3.12) به کاهش می یابد
![]() (3.13)
(3.13)
به همین ترتیب اجازه دهید  یک بردار واحد معین باشد که راضی باشد
یک بردار واحد معین باشد که راضی باشد  ، و بگذارید
، و بگذارید

و

به ترتیب برآورد مربوط به یک بردار منفرد و یک مقدار واحد را نشان می دهد. پس اینجا

و (3.12) به کاهش می یابد
![]() (3.14)
(3.14)
این بخش را با ذکر تفاوت بین ضریب مستطیل (1.6) و مقدار ریلی تعمیم یافته (GRQ) پیشنهاد شده توسط Ostrowski به پایان خواهیم رساند [ 26 ]. اجازه دهید ![]() یک ماتریس مربع عمومی (غیر عادی) از نظم n باشد و اجازه دهید
یک ماتریس مربع عمومی (غیر عادی) از نظم n باشد و اجازه دهید ![]() و
و ![]() دو
دو ![]() بردار باشد که
بردار باشد که  در جایی که
در جایی که ![]() نشانگر انتقال جفت است ، راضی باشد
نشانگر انتقال جفت است ، راضی باشد ![]() . سپس GRQ ،
. سپس GRQ ،
![]() (3.15)
(3.15)
با هدف تقریب یک مقدار ویژه از ![]() "مشترک" برای
"مشترک" برای ![]() و
و ![]() . برای بحث های دقیق در مورد GRQ و خصوصیات آن به [25-27،29،40] مراجعه کنید.
. برای بحث های دقیق در مورد GRQ و خصوصیات آن به [25-27،29،40] مراجعه کنید.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
در این بخش ، ما نکات و حقایقی را که برای بحث در آینده لازم است ، معرفی می کنیم. مانند قبل ![]() یک
یک ![]() ماتریس واقعی را با نشان می دهد
ماتریس واقعی را با نشان می دهد 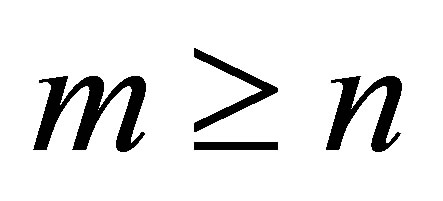 . اجازه دهید
. اجازه دهید
![]() (2.1)
(2.1)
یک SVD از ![]() ، که در آن
، که در آن  یک IS
یک IS ![]()
ماتریس متعامد ، 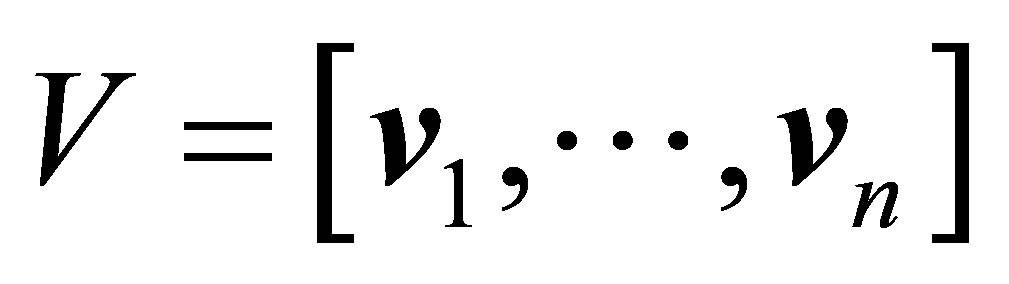 یک
یک ![]() ماتریس متعامد است ، و
ماتریس متعامد است ، و 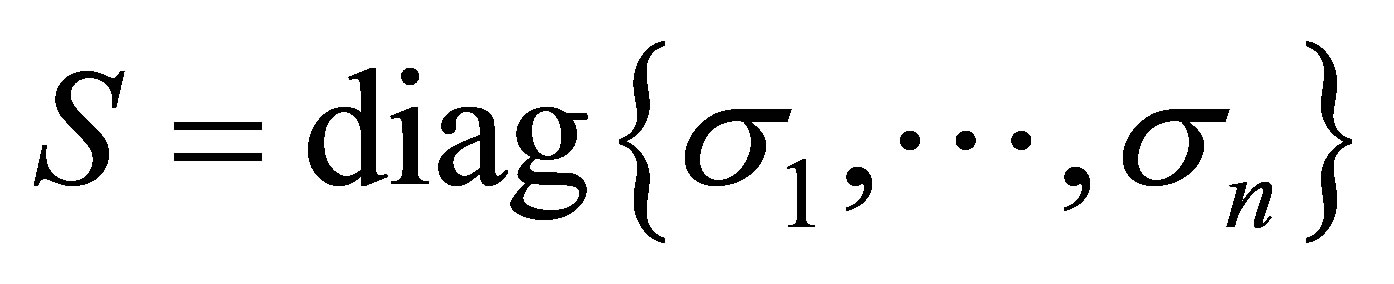 یک
یک ![]() ماتریس مورب است. مقادیر منحصر به فرد
ماتریس مورب است. مقادیر منحصر به فرد ![]() فرض می شود که منفی نبوده و برای ارضای آن مرتب شده باشد
فرض می شود که منفی نبوده و برای ارضای آن مرتب شده باشد
![]() (2.2)
(2.2)
ستون از ![]() و
و ![]() به نام به سمت چپ بردار منحصر به فرد و بردار منحصر به فرد راست، به ترتیب. این بردارها با معادلات مرتبط هستند
به نام به سمت چپ بردار منحصر به فرد و بردار منحصر به فرد راست، به ترتیب. این بردارها با معادلات مرتبط هستند
![]() (2.3)
(2.3)
نتیجه بعدی (2.1) برابری است
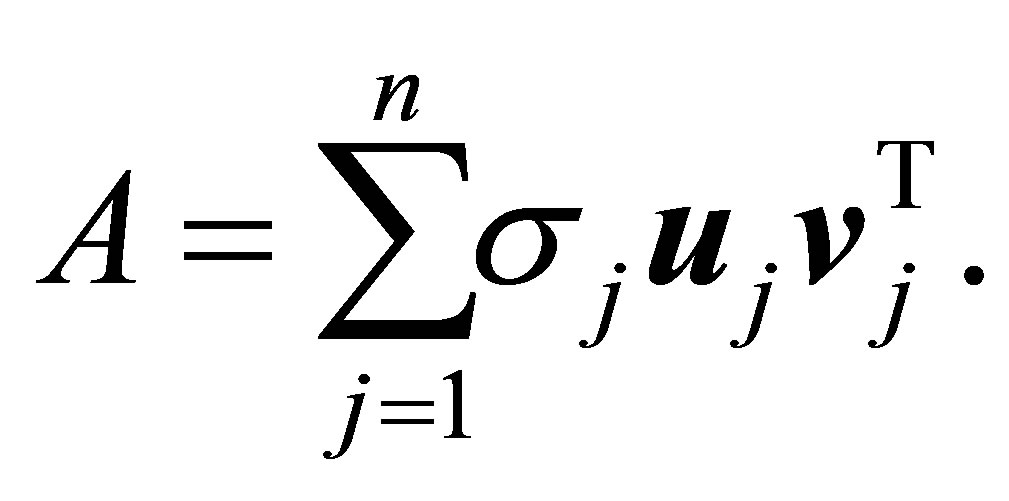 (2.4)
(2.4)
علاوه بر این ، اجازه دهید ![]() نشان می دهد رتبه از
نشان می دهد رتبه از ![]() . سپس ، به وضوح ،
. سپس ، به وضوح ،
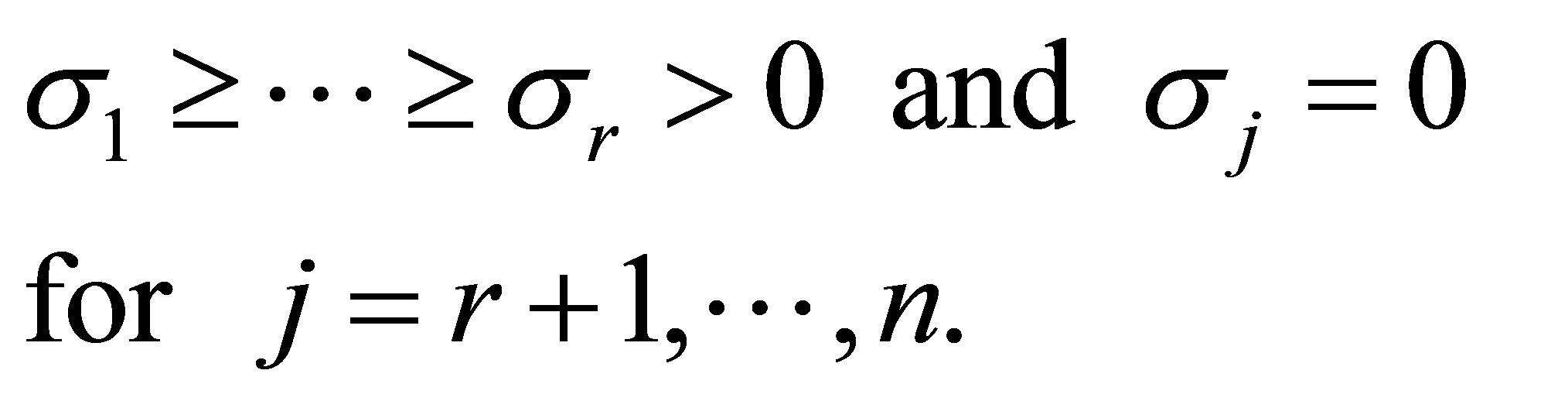 (2.5)
(2.5)
بنابراین (2.4) را می توان دوباره نوشت
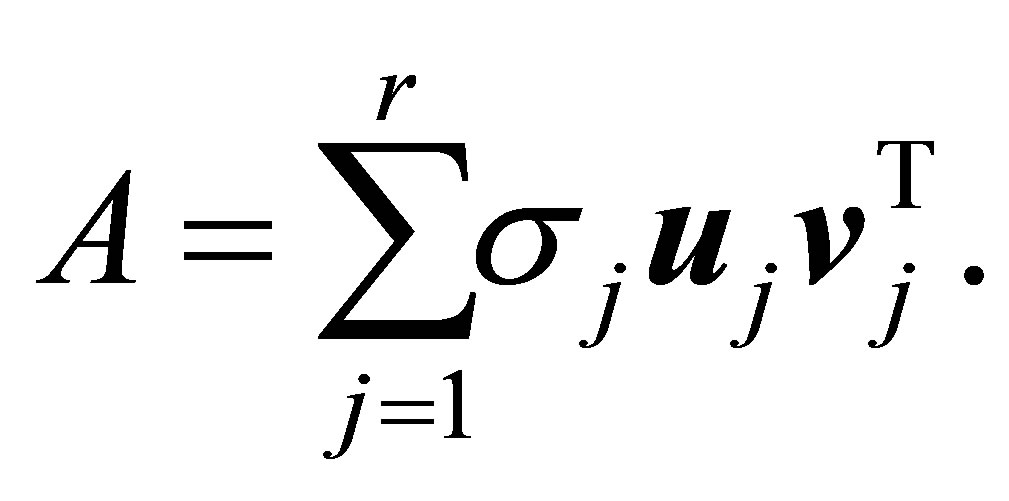 (2.6)
(2.6)
اجازه دهید ماتریس ها
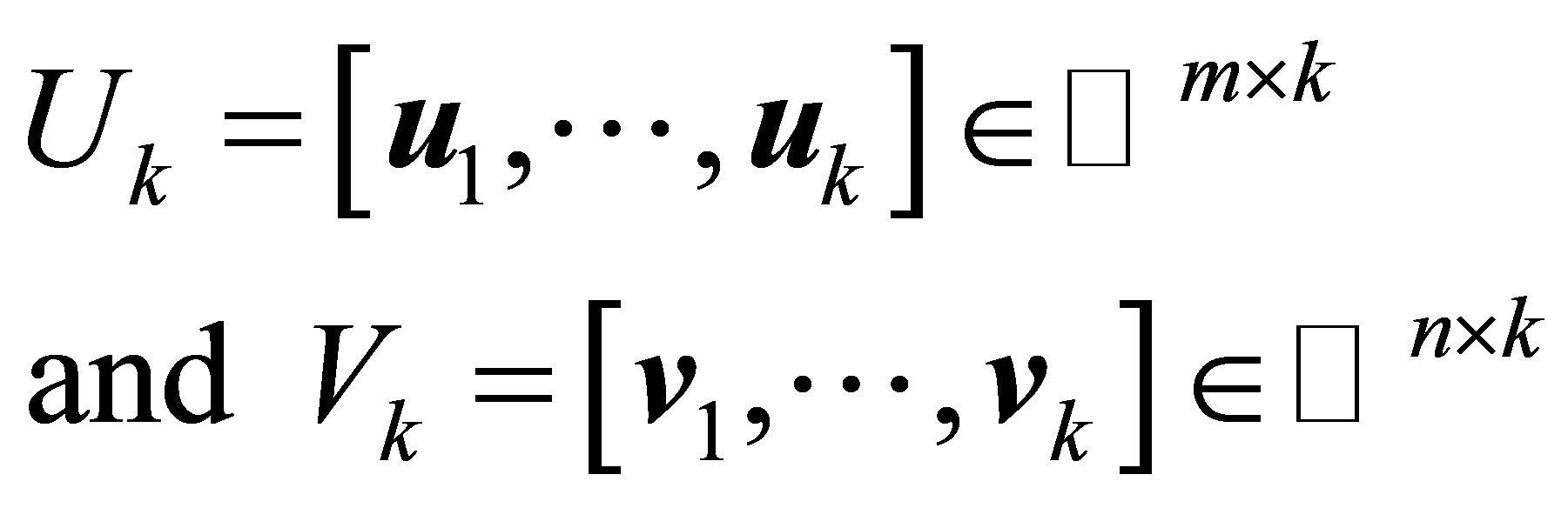 (2.7)
(2.7)
به ترتیب از اولین ![]() ستون های U ساخته شده
ستون های U ساخته شده ![]() است. اجازه دهید
است. اجازه دهید 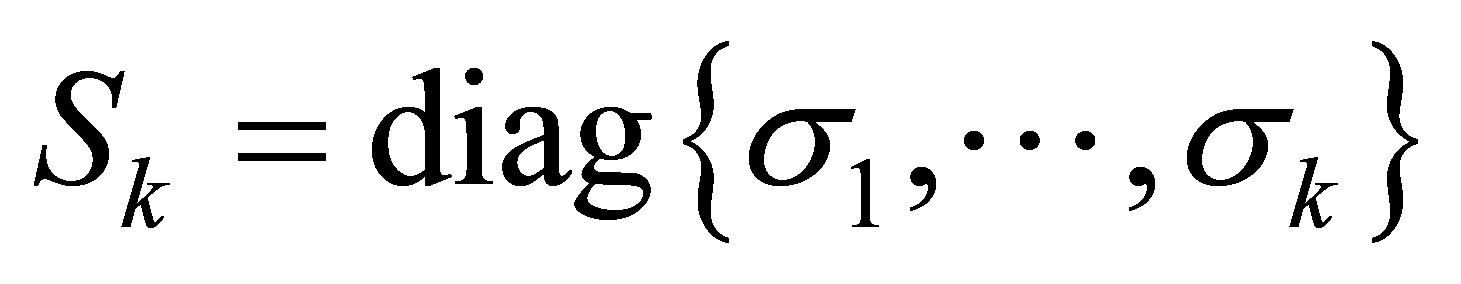 یک
یک ![]() ماتریس مورب باشد. سپس ماتریس
ماتریس مورب باشد. سپس ماتریس
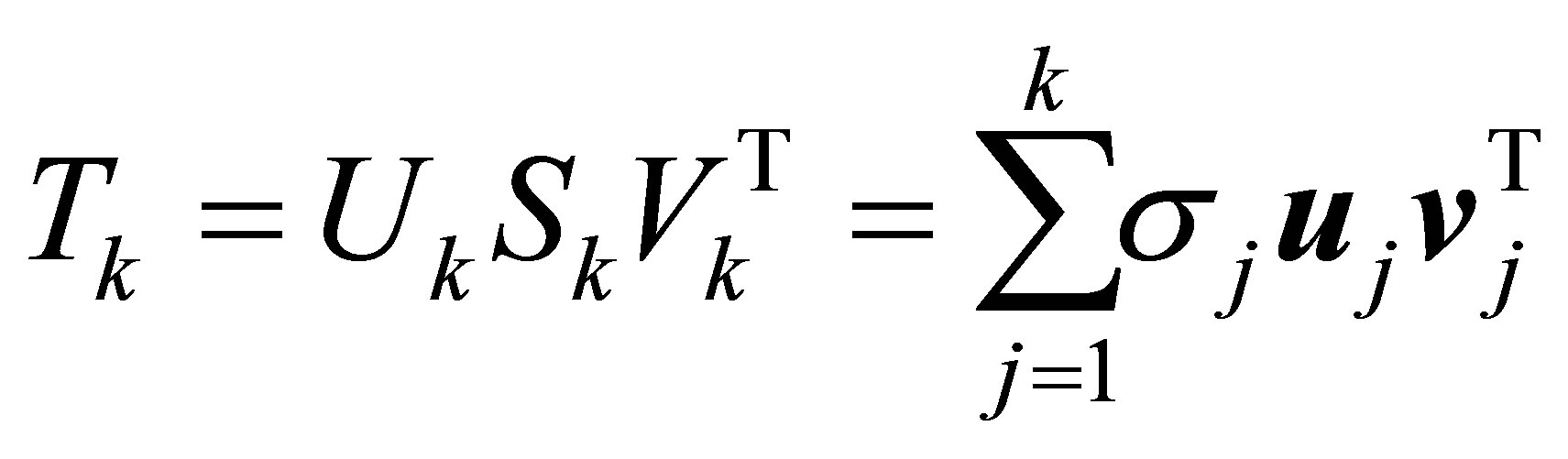 (2.8)
(2.8)
![]() مرتبه- SVD کوتاه شده از نامیده می شود
مرتبه- SVD کوتاه شده از نامیده می شود ![]() .
.
اجازه دهید 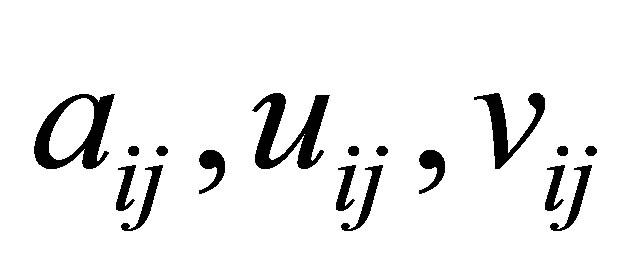 ، به ترتیب
، به ترتیب ![]() ورودی های ماتریس را
ورودی های ماتریس را 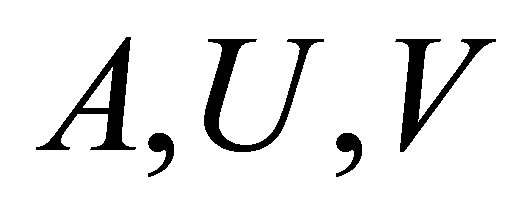 مشخص کنید. سپس (2.4) نشان می دهد که
مشخص کنید. سپس (2.4) نشان می دهد که
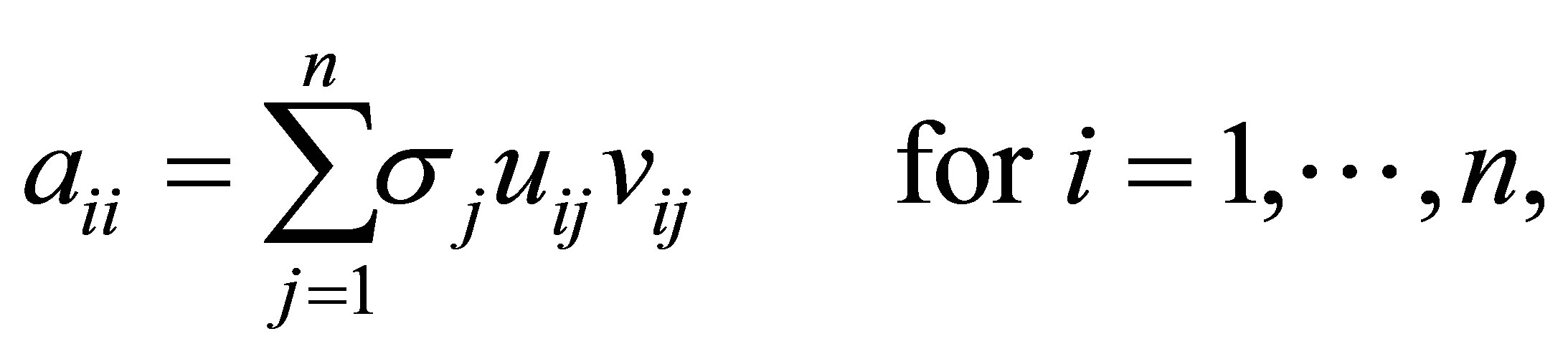 (2.9)
(2.9)
و
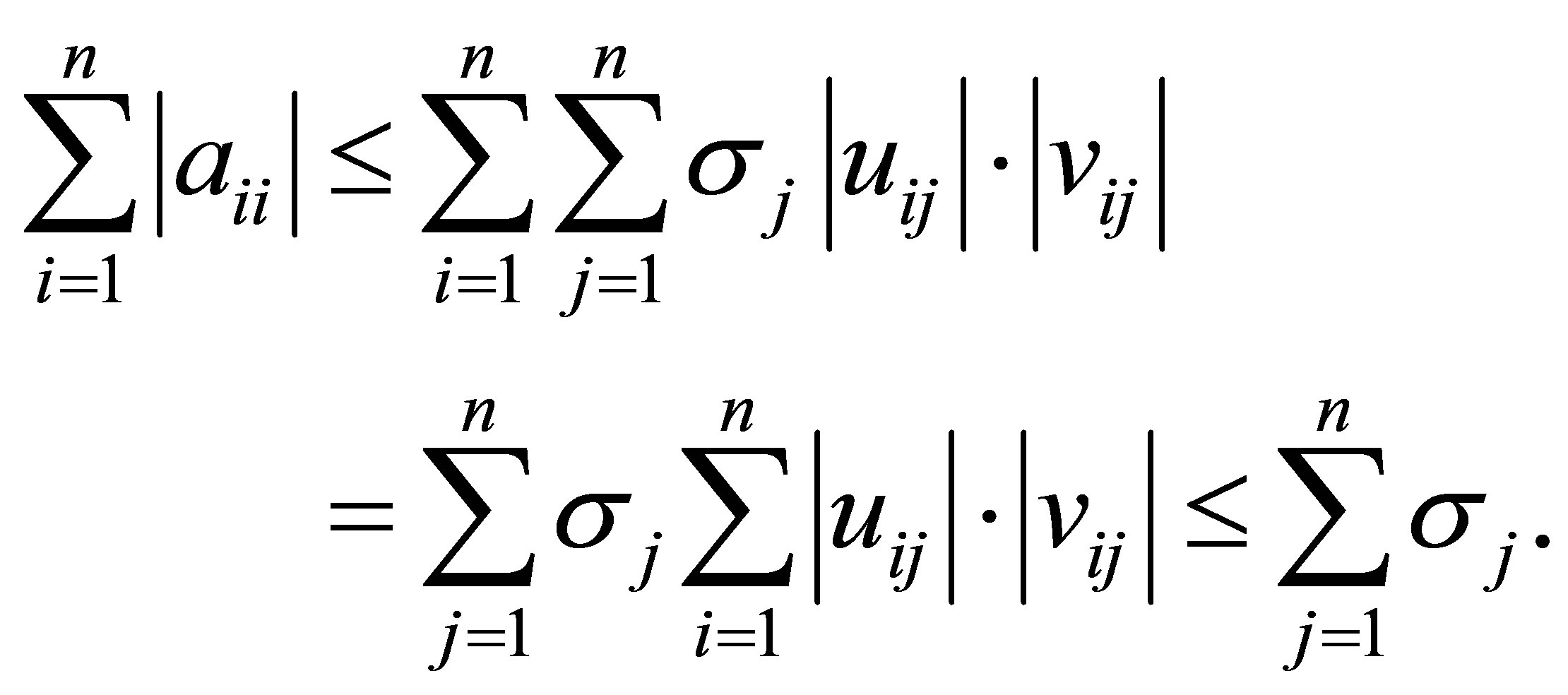 (2.10)
(2.10)
که در آن آخرین نابرابری زیر از نابرابری CauchySchwarz و این واقعیت است که ستون از ![]() و
و ![]() باید طول واحد.
باید طول واحد.
یکی دیگر از ویژگیهای مفید مفاهیم بزرگنمایی و هنجارهای یکپارچه بی ثبات است. به یاد بیاورید که در صورت برابر بودن یک هنجار ماتریس ![]() به
به ![]() صورت واحد تغییر نمی کند
صورت واحد تغییر نمی کند
![]() (2.11)
(2.11)
برای هر ماتریس 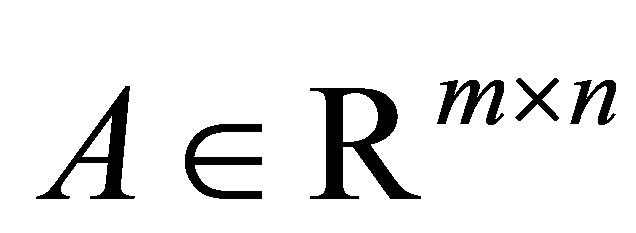 و هر جفت ماتریس واحد راضی هستند
و هر جفت ماتریس واحد راضی هستند 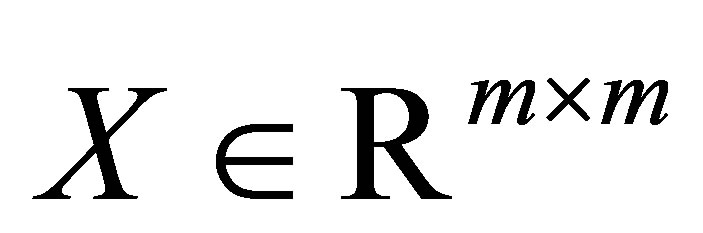 و
و 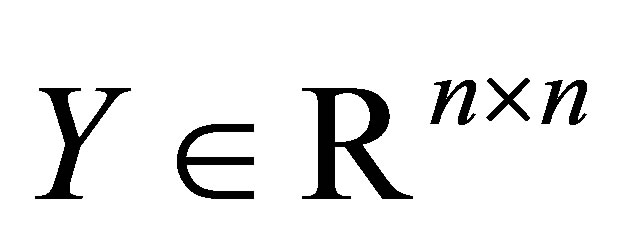 . اجازه دهید
. اجازه دهید ![]() و
و ![]() یک جفت
یک جفت ![]() ماتریس داده شده با مقادیر منفرد باشد
ماتریس داده شده با مقادیر منفرد باشد
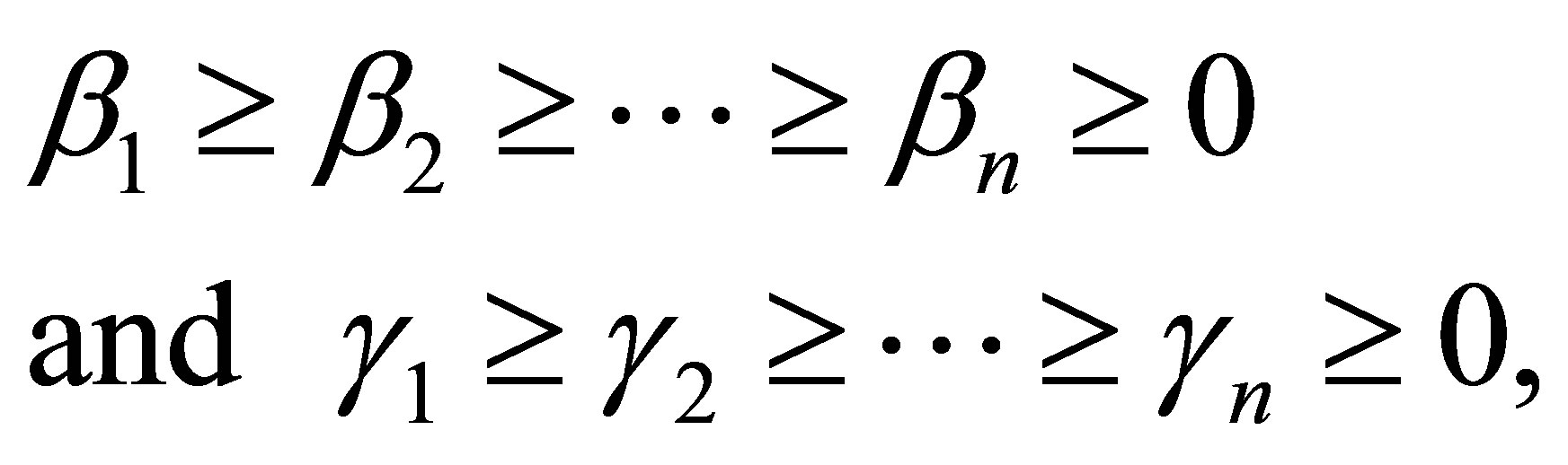
به ترتیب. اجازه دهید 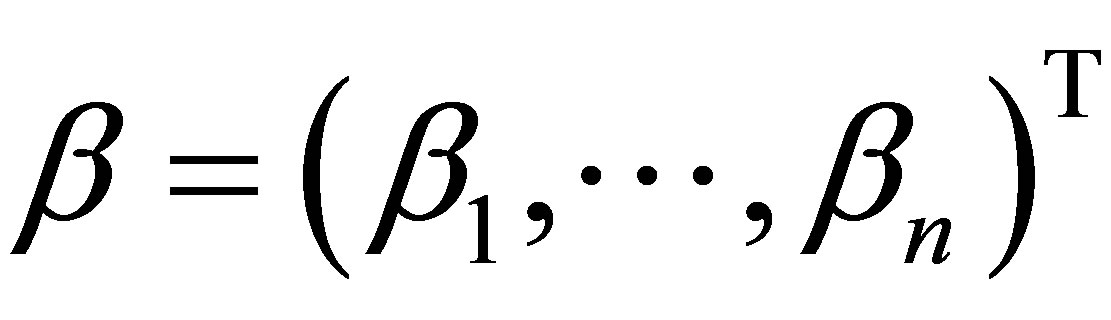 و
و 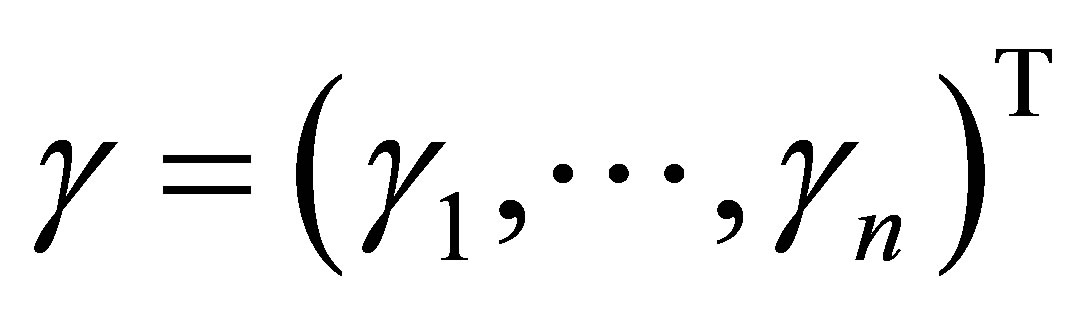
معنی مربوطه ![]() -vectors از ارزش منحصر به فرد. سپس رابطه بزرگ نمایی ضعیف
-vectors از ارزش منحصر به فرد. سپس رابطه بزرگ نمایی ضعیف 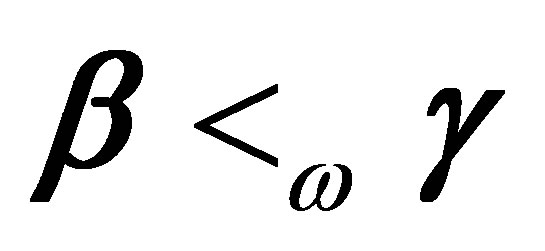 به این معنی است که این بردارها نابرابری ها را برآورده می کنند
به این معنی است که این بردارها نابرابری ها را برآورده می کنند
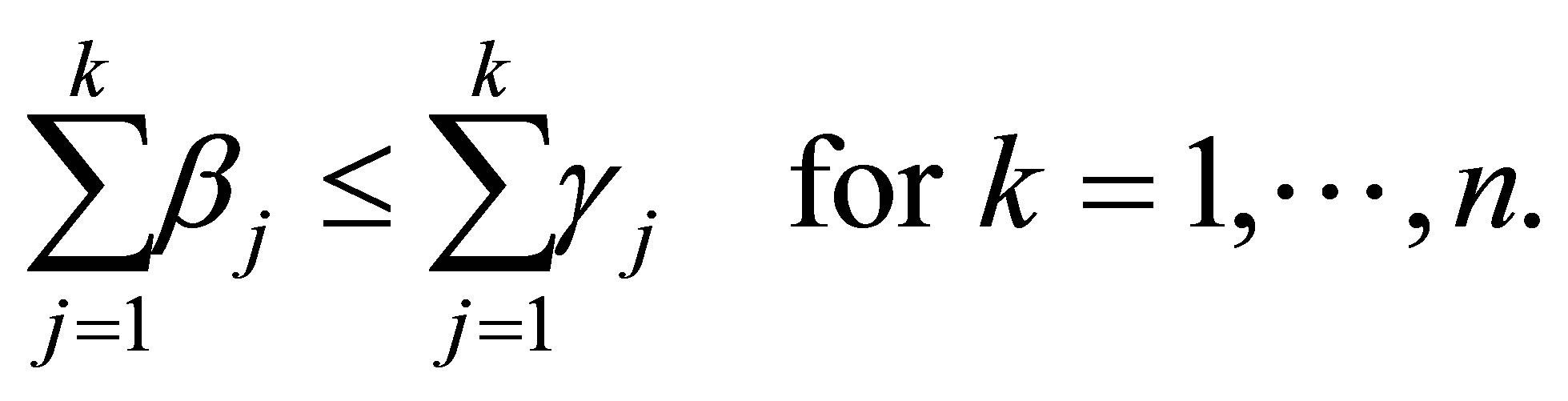 (2.12)
(2.12)
در این حالت می گوییم که ![]() توسط ضعیف بزرگ شده
توسط ضعیف بزرگ شده ![]() یا مقادیر منفرد B به طور ضعیفی توسط آن بزرگ شده است
یا مقادیر منفرد B به طور ضعیفی توسط آن بزرگ شده است ![]() . قضیه تسلط Ky Fan [ 11 ] این دو مفهوم را با هم مرتبط می کند. این مقاله می گوید اگر مقادیر منفرد
. قضیه تسلط Ky Fan [ 11 ] این دو مفهوم را با هم مرتبط می کند. این مقاله می گوید اگر مقادیر منفرد ![]() توسط آن
توسط آن ![]() نابرابری بزرگ شود
نابرابری بزرگ شود
![]() (2.13)
(2.13)
برای هر هنجار واحدی ثابت است. برای اثبات دقیق این واقعیت ، به عنوان مثال ، [1،11،17،22] را ببینید. مشهورترین مثال از یک هنجار منحصر به فرد ، شاید هنجار ماتریس Frobenius است
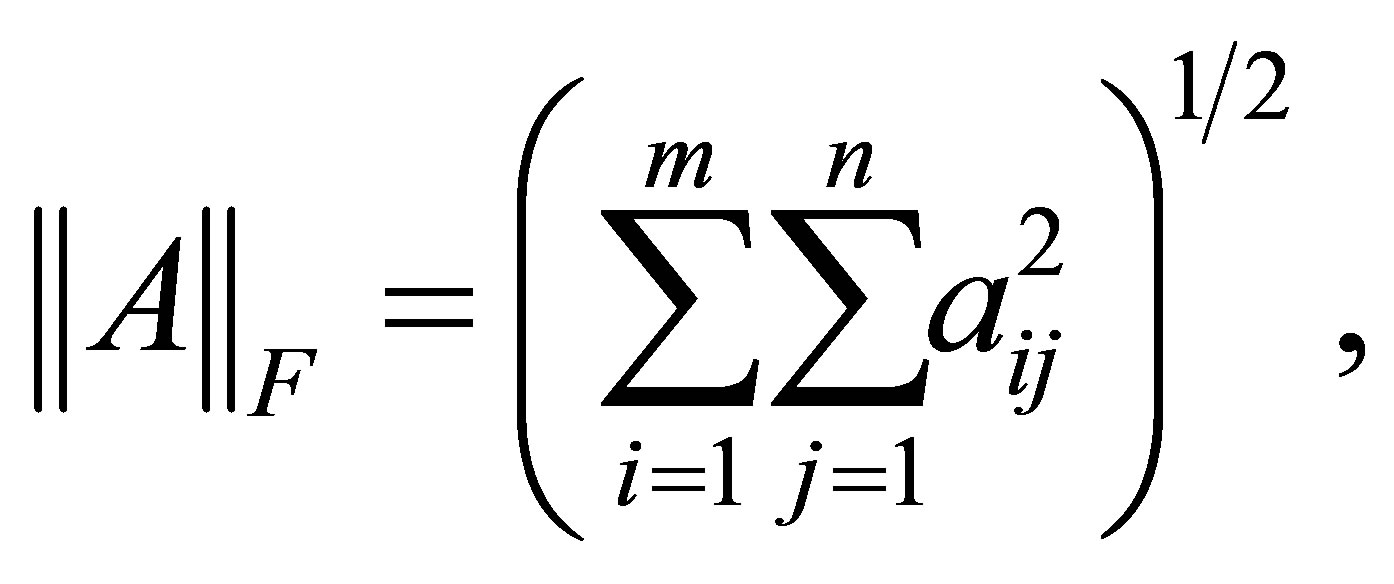 (2.14)
(2.14)
که راضی می کند
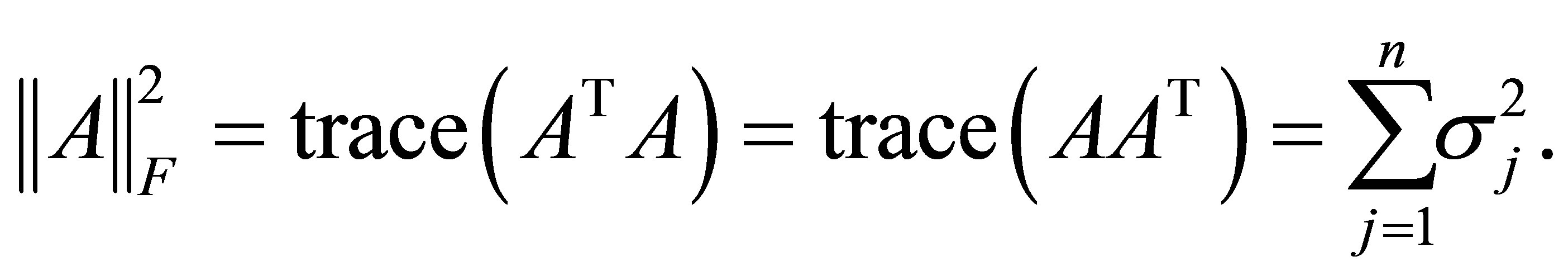 (2.15)
(2.15)
مثالهای دیگر Schatten ![]() -norms است ،
-norms است ،
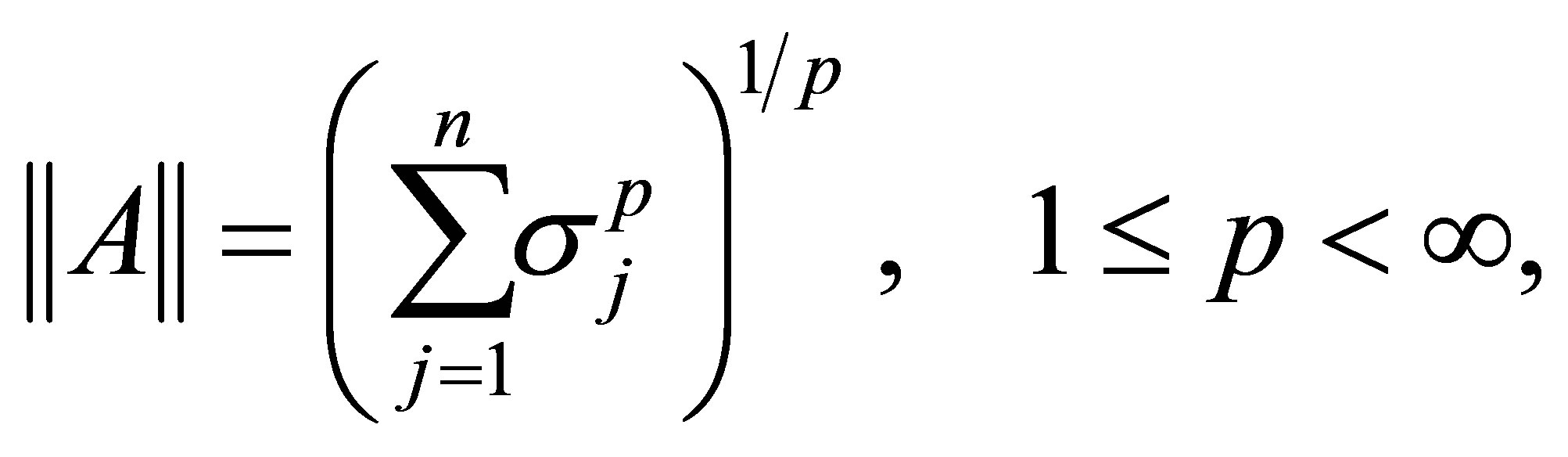 (2.16)
(2.16)
و Ky Fan ![]() -norms ،
-norms ،
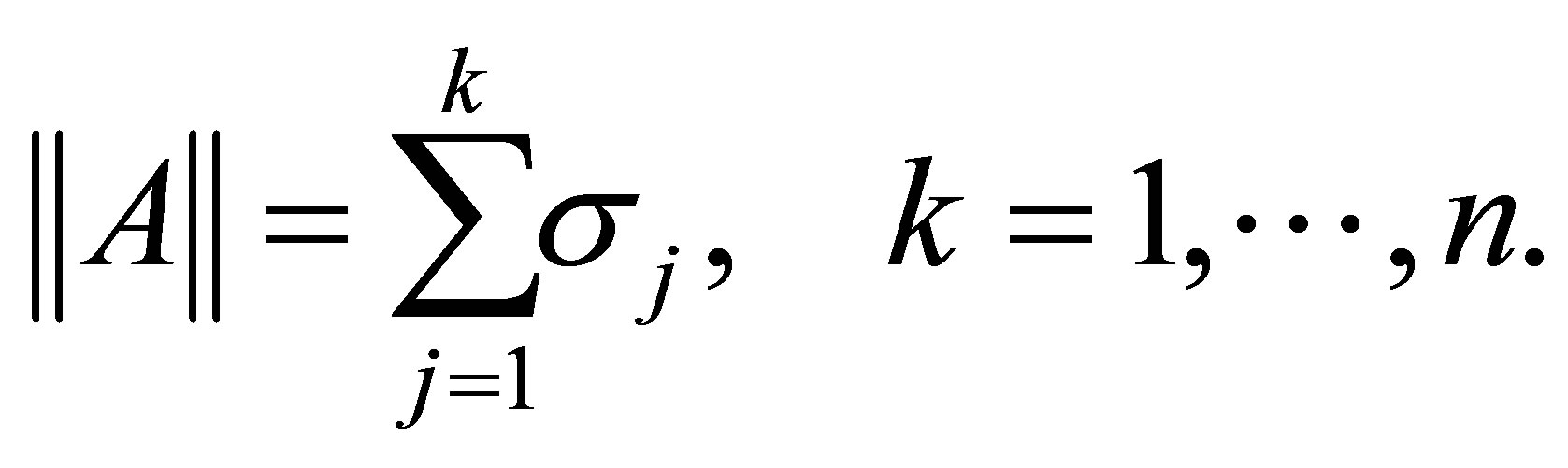 (2.17)
(2.17)
هنجار کمیاب ،
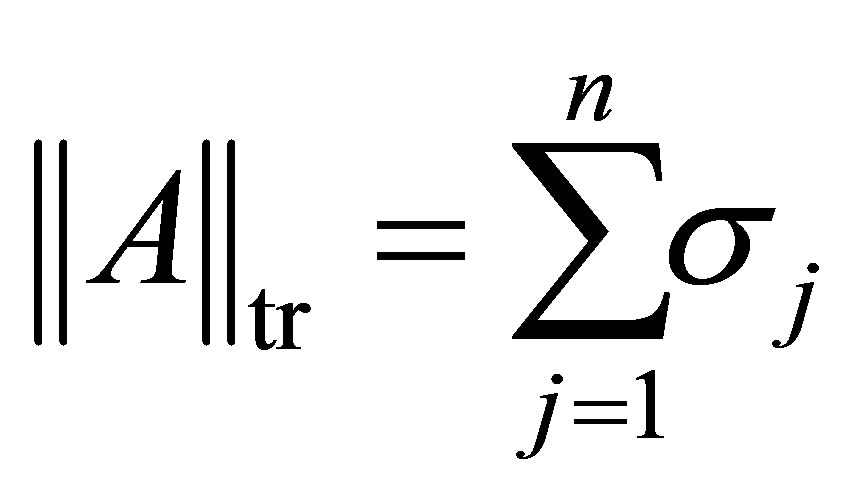 (2.18)
(2.18)
برای ![]() و
و ![]() در حالی که هنجار طیفی (2 هنجار) بدست می آید
در حالی که هنجار طیفی (2 هنجار) بدست می آید
![]() (2.19)
(2.19)
مطابقت دارد ![]() و
و 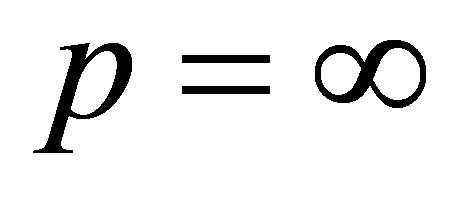 .
.
در آخر ، اجازه دهید ![]() و
و ![]() یک جفت عدد صحیح مثبت داشته باشید ، به گونه ای که
یک جفت عدد صحیح مثبت داشته باشید ، به گونه ای که
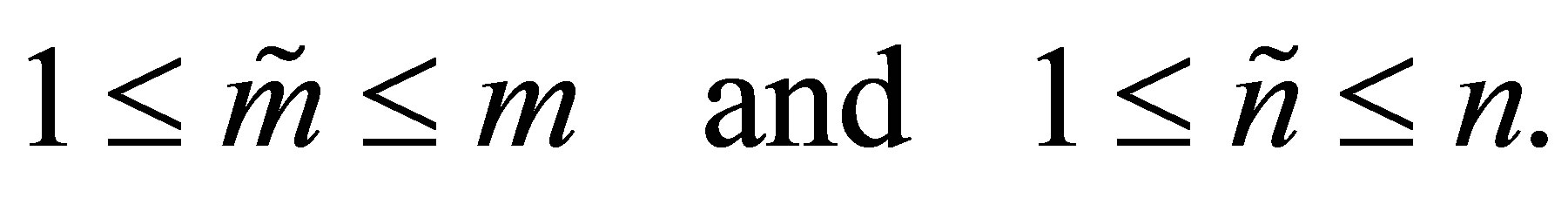
سپس
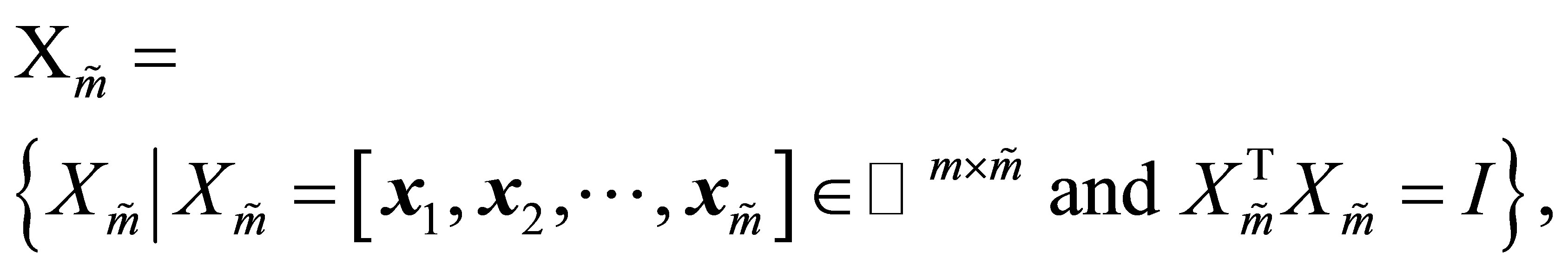 (2.20)
(2.20)
و
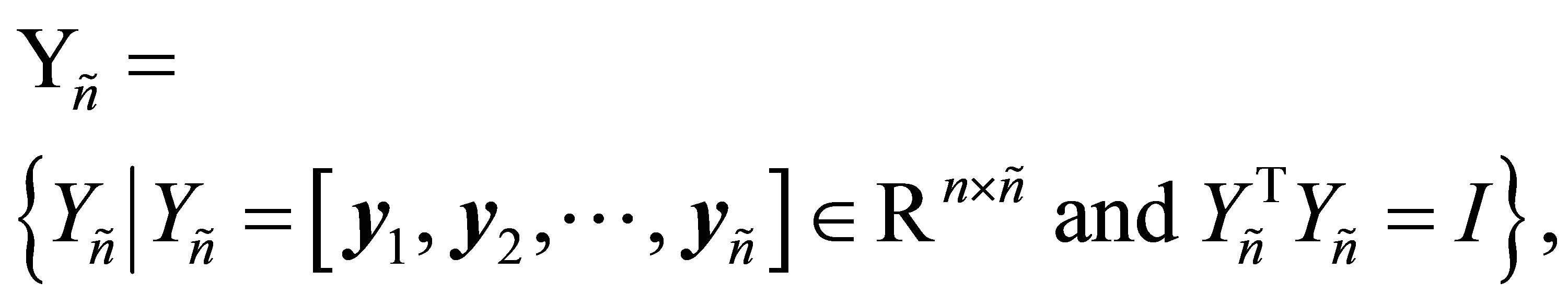 (2.21)
(2.21)
منیفولدهای مربوط به استیفل را نشان می دهد. یعنی ![]() مجموعه ای از تمام
مجموعه ای از تمام ![]() ماتریس های واقعی با ستون های متعادل ، در حالی
ماتریس های واقعی با ستون های متعادل ، در حالی ![]() که مجموعه تمام
که مجموعه تمام ![]() ماتریس های واقعی با ستون های متعادل است.
ماتریس های واقعی با ستون های متعادل است.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
پیشرفت در ریاضیات خالص
جلد 3 شماره 9 B (2013) ، شناسه مقاله: 41122،17 صفحه DOI: 10.4236 / apm.2013.39A2002
از مقادیر ویژه تا مقادیر واحد: یک بررسی
خدمات هیدرولوژیکی ، اورشلیم ، اسرائیل
ایمیل: dax20@water.gov.il
کپی رایت © 2013 آکیا داکس. این یک مقاله دسترسی آزاد است که تحت مجوز Creative Commons Attribution توزیع شده است ، استفاده ، توزیع و تولید مثل بدون محدودیت در هر رسانه را مجاز می داند ، به شرط آنکه اثر اصلی به درستی ذکر شود.
دریافت شده در 15 آگوست 2013؛ تجدید نظر شده در 15 سپتامبر 2013 ؛ 21 سپتامبر 2013 پذیرفته شده است
کلمات کلیدی: مقادیر ویژه؛ مقادیر واحد ؛ Rayleigh Quotient؛ ماتریس های ضریب متعامد؛ برابری فاکتورهای متعامد؛ قضیه اكارت-یانگ؛ اصول Extremum Ky Fan
چکیده
تشابه بین مقادیر ویژه و مقادیر واحد چهره های بسیاری دارد. بررسی کنونی چندین نمونه از این تشبیه را گرد هم آورده است. یک مثال مربوط به شباهت بین مقدارهای ریلی متقارن و مقدارهای ریلی مستطیل است. بسیاری از خواص مفید ساقه مقادیر ویژه از قضیه مینیماکس Courant-Fischer ، از قضیه Weyl ، و نتیجه آن است. جنبه دیگر مربوط به نسخه های "مستطیلی" این قضیه ها است. مقایسه خصوصیات ماتریس های Rayleigh Quotient با ماتریس های Orthogonal Quotient موضوع را در نور جدید روشن می کند. برابری ضرایب متعامد یک نتیجه اخیر است که مسئله حداقل هنجار اكارت-یانگ را به مسئله حداكثر هنجار معادل تبدیل می كند. این مسئله پیوند شگفت انگیزی بین قضیه اكارت-یانگ و حداكثر اصل Ky Fan را آشكار می كند. می بینیم که این دو قضیه دو روی یک سکه را منعکس می کنند: اصل حداکثر کلی تری وجود دارد که هر دو قضیه به راحتی از آن گرفته می شوند. Ky Fan از اصل extremeum خود (در مورد ردیابی ماتریس ها) برای استخراج نتایج آنالوگ در تعیین ماتریس های مثبت Rayleigh Quotients استفاده کرده است. اصل جدید extremeum این نتایج را به ماتریس های مستطیل مستطیل گسترش می دهد. آوردن همه این موضوعات زیر یک سقف ، بینش جدیدی در مورد روابط جذاب بین مقادیر ویژه و ارزشهای منفرد فراهم می کند.
1. مقدمه
اجازه دهید ![]() یک
یک ![]() ماتریس متقارن واقعی باشد و اجازه دهید
ماتریس متقارن واقعی باشد و اجازه دهید
 یک بردار غیر صفر داده شده باشد. سپس شناخته شده Rayleigh Quotient به این صورت تعریف می شود
یک بردار غیر صفر داده شده باشد. سپس شناخته شده Rayleigh Quotient به این صورت تعریف می شود
![]() (1.1)
(1.1)
یکی از انگیزه های این تعریف در مشاهده زیر نهفته است. بگذارید ![]() یک عدد واقعی داده شود. سپس ارزش ویژه
یک عدد واقعی داده شود. سپس ارزش ویژه ![]() ای از آن وجود دارد به
ای از آن وجود دارد به ![]() گونه ای که
گونه ای که
![]() (1.2)
(1.2)
و مقدار ![]() آن مسئله حداقل هنجار را حل می کند
آن مسئله حداقل هنجار را حل می کند
![]() (1.3)
(1.3)
توسط داده شده است ![]() . به عبارت دیگر ،
. به عبارت دیگر ، ![]() برآورد ارزش ویژه مربوط به آن را ارائه می دهد
برآورد ارزش ویژه مربوط به آن را ارائه می دهد ![]() . ترکیب این برآورد با تکرار معکوس باعث تکرار تکرار مقدار ریلی می شود. از دیگر ویژگیهای مرتبط می توان به نابرابری های مینیمکس Courant-Fischer ، قضیه یکنواختی ویل و بسیاری دیگر از نتایج ناشی از این مشاهدات اشاره کرد. به طور خاص ، بزرگترین و کوچکترین مقادیر ویژه برای
. ترکیب این برآورد با تکرار معکوس باعث تکرار تکرار مقدار ریلی می شود. از دیگر ویژگیهای مرتبط می توان به نابرابری های مینیمکس Courant-Fischer ، قضیه یکنواختی ویل و بسیاری دیگر از نتایج ناشی از این مشاهدات اشاره کرد. به طور خاص ، بزرگترین و کوچکترین مقادیر ویژه برای ![]() ارضای
ارضای
![]() (1.4)
(1.4)
و
![]() (1.5)
(1.5)
به ترتیب. برای بحث دقیق در مورد مقدار ریلی و خصوصیات آن ، به عنوان مثال ، [1-41] را ببینید.
س thatالی که مطالعه ما را آغاز می کند این است که چگونه تعریف Rayleigh Quotient را برای تخمین مقدار منفرد یک ماتریس مستطیل شکل عمومی گسترش دهیم ، جایی که اصطلاح "مستطیل شکل" به این معنی است که ماتریس لزوماً متقارن یا مربع نیست. به عبارت دقیق تر ، اجازه دهید ![]() یک
یک ![]() ماتریس واقعی باشد
ماتریس واقعی باشد  ، و اجازه دهید
، و اجازه دهید  و
و  یک جفت بردار غیر صفر باشد. سپس ما به دنبال یک تابع اسکالر هستیم
یک جفت بردار غیر صفر باشد. سپس ما به دنبال یک تابع اسکالر هستیم![]() ، و
، و ![]() ،
،  مثلاً ، مقدار آنها تقریباً با ارزش مفرد "متناظر" برابر است
مثلاً ، مقدار آنها تقریباً با ارزش مفرد "متناظر" برابر است ![]() . پاسخ توسط مستطیل مستطیل داده شده است ،
. پاسخ توسط مستطیل مستطیل داده شده است ،
![]() (1.6)
(1.6)
که  نشانگر هنجار بردار اقلیدسی است. توجیهات این تعریف در بخش 3 آورده شده است. در آنجا نشان داده شده است که خصوصیات مقدار مستطیل (1.6) به خصوصیات مقدار ریلی شباهت دارد (1.1). در واقع ، همانطور که بررسی ما نشان می دهد ، شباهت فوق یک قانون کلی تر را منعکس می کند: ویژگی های بهینه ماتریس های فاضلاب متعامد شبیه ماتریس های Rayleigh Quotient هستند (گسترش می یابند).
نشانگر هنجار بردار اقلیدسی است. توجیهات این تعریف در بخش 3 آورده شده است. در آنجا نشان داده شده است که خصوصیات مقدار مستطیل (1.6) به خصوصیات مقدار ریلی شباهت دارد (1.1). در واقع ، همانطور که بررسی ما نشان می دهد ، شباهت فوق یک قانون کلی تر را منعکس می کند: ویژگی های بهینه ماتریس های فاضلاب متعامد شبیه ماتریس های Rayleigh Quotient هستند (گسترش می یابند).
اجازه دهید  یک
یک ![]() ماتریس واقعی با باشد
ماتریس واقعی با باشد
![]() ستونهای عادی. بگذارید
ستونهای عادی. بگذارید  واقعی باشد
واقعی باشد
![]() ماتریس با
ماتریس با ![]() ستون های متعادل. سپس یک
ستون های متعادل. سپس یک ![]() ماتریس از فرم
ماتریس از فرم
![]() (1.7)
(1.7)
ماتریس Orthogonal Quotient نامیده می شود. توجه داشته باشید که
![]() (1.8)
(1.8)
بنابراین ورودی ها از ![]() مقدار مطلق برابر با ضریب های مستطیل مربوطه برخوردارند. ماتریس های فرم (1.7) را می توان ماتریس های Rayleigh Quotient "مستطیل شکل" دید. تعریف سنتی از ماتریس های متقارن Rayleigh Quitient به ماتریس های متقارن فرم اشاره دارد
مقدار مطلق برابر با ضریب های مستطیل مربوطه برخوردارند. ماتریس های فرم (1.7) را می توان ماتریس های Rayleigh Quotient "مستطیل شکل" دید. تعریف سنتی از ماتریس های متقارن Rayleigh Quitient به ماتریس های متقارن فرم اشاره دارد
![]() (1.9)
(1.9)
که در آن ![]() و
و ![]() تعریف همانطور که در بالا، به عنوان مثال، [20،30،36]. متریال های متقارن Rayleigh Quitient این فرم را بعضی اوقات مقطع می نامند. یک کلاس بزرگتر از ماتریس های Rayleigh Quotients در [ 34 ] در نظر گرفته شده است . این ماتریس ها فرم دارند
تعریف همانطور که در بالا، به عنوان مثال، [20،30،36]. متریال های متقارن Rayleigh Quitient این فرم را بعضی اوقات مقطع می نامند. یک کلاس بزرگتر از ماتریس های Rayleigh Quotients در [ 34 ] در نظر گرفته شده است . این ماتریس ها فرم دارند
![]() (1.10)
(1.10)
کجا ![]() یک ماتریس مربع عمومی (غیر عادی) از نظم وجود دارد
یک ماتریس مربع عمومی (غیر عادی) از نظم وجود دارد ![]() .
. ![]() ماتریس
ماتریس ![]() فرض بر این است به رتبه ستون کامل باشد، و
فرض بر این است به رتبه ستون کامل باشد، و ![]() ماتریس
ماتریس ![]() نشان دهنده یک معکوس چپ
نشان دهنده یک معکوس چپ ![]() . یعنی یک ماتریس راضی کننده
. یعنی یک ماتریس راضی کننده . ماتریس فرمها (1.9) و (1.10) نقش مهمی در روش ریلی-ریتز و در روشهای فضایی Krylov دارند ، به عنوان مثال ، [30،34]. در این زمینه ادبیات غنی در مورد مرزهای باقیمانده برای مقادیر ویژه و فضاهای ویژه وجود دارد. برای مثال ، به [19-21،30،32،34،36] مراجعه کنید. برنامه های دیگر ماتریس های Rayleigh Quotient در الگوریتم های بهینه سازی بوجود می آیند که سعی می کنند تقریب های خود را در یک منیفولد خاص Stiefel حفظ کنند ، به عنوان مثال ، [6،7،9،35].
. ماتریس فرمها (1.9) و (1.10) نقش مهمی در روش ریلی-ریتز و در روشهای فضایی Krylov دارند ، به عنوان مثال ، [30،34]. در این زمینه ادبیات غنی در مورد مرزهای باقیمانده برای مقادیر ویژه و فضاهای ویژه وجود دارد. برای مثال ، به [19-21،30،32،34،36] مراجعه کنید. برنامه های دیگر ماتریس های Rayleigh Quotient در الگوریتم های بهینه سازی بوجود می آیند که سعی می کنند تقریب های خود را در یک منیفولد خاص Stiefel حفظ کنند ، به عنوان مثال ، [6،7،9،35].
کلاس سوم ماتریس های Rayleigh Quotient از (1.7) با گرفتن بدست می آید  . این ماتریس ها در مرزهای باقیمانده برای مقادیر منفرد و فضاهای مجزا درگیر هستند ، به عنوان مثال ، [2،21].
. این ماتریس ها در مرزهای باقیمانده برای مقادیر منفرد و فضاهای مجزا درگیر هستند ، به عنوان مثال ، [2،21].
با این حال ، بررسی ما به جهات مختلف تبدیل می شود. هدف این است که خواص بهینه سازی ماتریس های ضریب متعامد را کشف کند. مقایسه این خصوصیات با ماتریس های متقارن Rayleigh Quotients مشاهدات بسیار جالبی را نشان می دهد. در قلب این مشاهدات رابطه تعجب آور بین قضیه حداقل هنجار اكارت-یانگ [ 5 ] و حداكثر اصل Ky Fan [ 10 ] وجود دارد.
قضیه اكارت-یانگ مسئله تقریب یك ماتریس با ماتریس دیگر با درجه پایین را در نظر می گیرد. راه حل این مشکل را نیز به اشمیت نسبت می دهند [ 31] به [17 ، pp. 137،138 ~] و [33 ، p. 76] مراجعه کنید. نیاز به تقریب های سطح پایین یک ماتریس یک مشکل اساسی است که در بسیاری از برنامه ها بوجود می آید ، به عنوان مثال [3-5،8،14،15،18،33]. حداکثر اصل Ky Fan مسئله به حداکثر رساندن ردیابی یک ماتریس متقارن Rayleigh Quotient را در نظر می گیرد. همچنین یک نتیجه کاملاً شناخته شده است که کاربردهای بسیاری دارد ، به عنوان مثال ، [1،10-12 ، 16،22،28]. با این حال ، تاکنون ، این دو قضیه همیشه به عنوان نتایج مستقل و غیر مرتبط در نظر گرفته شده اند که مبتنی بر استدلال های مختلف هستند. برابری ضرایب متعامد یک نتیجه اخیر است که مسئله حداقل هنجار EckartYoung را به یک مسئله حداکثر هنجار معادل تبدیل می کند. این شباهت شگفت آور بین قضیه اكارت-یانگ و حداكثر اصل Ky Fan را آشكار می كند. می بینیم که این دو قضیه دو روی یک سکه را منعکس می کنند: یک قاعده حداکثر کلی تری وجود دارد که هر دو قضیه به راحتی از آن گرفته می شوند.
طرح بررسی ما به شرح زیر است. این کار با معرفی برخی نکات و حقایق ضروری آغاز می شود. سپس مشخص می شود که خصوصیات اساسی مقدار مستطیل (1.6) را نشان می دهد ، نشان می دهد که تعدادی از کمترین مشکلات نرمال شبیه به 1.3 را حل می کند. یک خطای محدود شده ، شبیه به (1.2) ، ما را قادر می سازد فاصله بین ![]() و نزدیکترین مقدار منفرد را محدود کنیم
و نزدیکترین مقدار منفرد را محدود کنیم ![]() .
.
جنبه دیگری از تشبیه بین مقادیر ویژه و مقادیر واحد در بخش 4 بررسی شده است ، که در آن نسخه های "مستطیلی" قضیه مینیمکس Courant-Fischer و قضیه Weyl را در نظر می گیریم. این راه را برای اثبات "سنتی" قضیه اكارت-یانگ هموار می كند. سپس با استفاده از قضیه تسلط Ky Fan می توان قضیه میرسکی را نتیجه گرفت.
رابطه بین ماتریس های متقارن Rayleigh Quotient و ماتریس های Orthogonal Quotients در بخش 5 مطالعه شده است. در آنجا نشان داده شده است که کمترین خصوصیات مربعات ماتریس های Orthogonal Quotient شبیه ماتریس های متقارن Rayleigh-Quotient است. یکی از پیامدهای این خصوصیات برابری ضرایب متعامد است که در بخش 6 استخراج شده است. همانطور که در بالا ذکر شد ، این برابری مسئله حداقل مربعات اكارت-یانگ را به حداكثر مسئله معادل تبدیل می كند ، كه تلاش می كند تا هنجار Frobenius از ماتریس عناصر متعامد را به حداكثر برساند فرم (1.7).
نسخه متقارن برابری فاکتورهای متعامد مسئله به حداکثر رساندن (یا به حداقل رساندن) ردپای ماتریس های متقارن رله را در نظر می گیرد. راه حل این مشکلات توسط اصول افراطی Ky Fan ارائه شده است. شباهت بین حداکثر شکل قضیه اكارت-یانگ و حداكثر اصل Ky Fan نشان می دهد كه هر دو مشاهده موارد خاصی از یك اصل افراطی كلی تر هستند. استنباط این اصل در بخش 8 انجام شده است. در آنجا نشان داده شده است که هر دو نتیجه از اصل حداکثر توسعه یافته به راحتی نتیجه می گیرند.
بررسی با بحث درباره برخی عواقب اصل توسعه یافته پایان می یابد. یک نتیجه یک برابری حداکثر حداکثر است که مسئله حداقل هنجار میرسکی را با مسئله حداکثر توسعه یافته مرتبط می کند. نوع دوم پیامدها مربوط به ردپای ماتریس های ضریب متعامد است. نتایج Ky Fan در مورد ردیابی ماتریس های متقارن ریلی [ 10 ] در مقالات اخیر وی [11،12] به محصولات مقادیر ویژه و عوامل تعیین شده گسترش یافت. اصل جدید extremeum گسترش این خصوصیات را به ماتریس های متعامد متعامد امکان پذیر می کند.
بررسی کنونی چندین نتیجه قدیمی و جدید را گرد هم آورده است. نتایج "قدیمی" با ارجاعات مناسب ارائه می شوند. در مقابل ، نتایج "جدید" بدون ارجاع به دست می آیند ، زیرا بیشتر آنها از مقاله تحقیقی اخیر [ 3 ] این نویسنده گرفته شده است. با این حال مقاله حاضر تعدادی از مشارکت ها را در بر می گیرد که در [ 3 ] موجود نیست. یک سهم در مورد گسترش قضیه 11 پشت هنجار Frobenius است. سهم دیگر حداقل و حداکثر برابری است که در بخش 9 معرفی شده است. تفاوت اصلی بین [ 3] و این مقاله در مفهوم آنها نهفته است. مقاله اول مقاله تحقیقی است که هدف آن ایجاد اصل گسترش افراطی است. این بررسی برخی از ویژگیهای جذاب تشبیه بین مقادیر ویژه و مقادیر واحد را نشان می دهد. برای این منظور ما چندین نتیجه ظاهرا غیر مرتبط را ارائه می دهیم. قرار دادن همه این مباحث در زیر یک سقف دید بهتری نسبت به این روابط دارد. توصیف نتایج بر روی ماتریس ها و بردارهای با ارزش واقعی متمرکز می شود. این کار ارائه را ساده می کند و به تمرکز بر ایده های اصلی کمک می کند. درمان این مورد باارزش کاملاً واضح است.
منبع
https://file.scirp.org/Html/2-5300515_41122.htm
از ویکیپدیا، دانشنامه آزاد
در تجزیه و تحلیل عددی ، تکرار معکوس (همچنین به عنوان روش توان معکوس شناخته می شود ) یک الگوریتم تکرار ارزش ویژه است . هنگامی که تقریب با مقدار ویژه مربوطه شناخته شده باشد به شما امکان می دهد یک بردار ویژه تقریبی پیدا کنید . این روش از نظر مفهومی مشابه روش قدرت است . به نظر می رسد که در اصل برای محاسبه فرکانس های تشدید در زمینه مکانیک سازه ساخته شده است. [1]
الگوریتم تکرار توان معکوس با یک تقریب شروع می شود 

جایی که 



در هر تکرار ، بردار 





فهرست
نظریه و همگرایی [ ویرایش ]
ایده اصلی تکرار قدرت انتخاب بردار اولیه است

تکرار معکوس همین کار را برای ماتریس انجام می دهد 







نتیجه گیری : این روش به بردار ویژه ماتریس همگرا می شود
به ویژه ، گرفتن 


سرعت همگرایی [ ویرایش ]
اجازه دهید میزان همگرایی روش را تجزیه و تحلیل کنیم .
روش قدرت شناخته شده است به همگرا خطی به حد، دقیق تر:
از این رو برای روش تکرار معکوس نتیجه مشابه به نظر می رسد:
این یک فرمول کلیدی برای درک همگرایی روش است. نشان می دهد که اگر










پیچیدگی [ ویرایش ]
الگوریتم تکرار معکوس نیاز به حل یک سیستم خطی یا محاسبه ماتریس معکوس دارد. برای ماتریس های غیر ساختاری (نه پراکنده ، نه Toeplitz ، ...) این نیاز دارد
گزینه های پیاده سازی [ ویرایش ]
روش با فرمول تعریف شده است:
با این وجود گزینه های متعددی برای اجرای آن وجود دارد.
محاسبه ماتریس معکوس یا حل سیستم معادلات خطی [ ویرایش ]
ما می توانیم فرمول را به روش زیر بازنویسی کنیم:
با تأکید بر اینکه برای پیدا کردن تقریب بعدی 

این انتخاب به تعداد تکرارها نیز بستگی دارد. ساده لوحانه ، اگر در هر تکرار یک سیستم خطی حل شود ، پیچیدگی k * O (n 3 ) خواهد بود ، جایی که k تعداد تکرار است. به طور مشابه ، محاسبه ماتریس معکوس و استفاده از آن در هر تکرار از پیچیدگی k * O (n 3 ) است . البته توجه داشته باشید که در صورت تخمین مقدار ویژه

معکوس کردن ماتریس معمولاً هزینه اولیه بیشتری دارد ، اما در هر تکرار هزینه کمتری دارد. برعکس ، حل سیستم معادلات خطی معمولاً هزینه اولیه کمتری دارد ، اما برای هر تکرار به عملیات بیشتری احتیاج دارد.
Tridiagonalization ، فرم Hessenberg [ ویرایش ]
اگر انجام بسیاری از تکرارها (یا تکرارهای کم ، اما برای بسیاری از بردارهای ویژه) ضروری باشد ، ممکن است عاقلانه باشد که ابتدا ماتریس را به شکل بالایی هسنبرگ بیاورید (برای ماتریس متقارن این حالت سه ضلعی خواهد بود ). که هزینه دارد

حل سیستم معادلات خطی برای هزینه های ماتریس سه وجهی


همچنین تبدیل به فرم هسنبرگ شامل ریشه های مربع و عمل تقسیم است که به طور جهانی توسط سخت افزار پشتیبانی نمی شوند.
انتخاب ثابت عادی  [ ویرایش ]
[ ویرایش ]
در پردازنده های هدف عمومی (به عنوان مثال تولید شده توسط اینتل) زمان اجرای جمع ، ضرب و تقسیم تقریباً برابر است. اما در سخت افزارهای جاسازی شده و / یا کم مصرف انرژی ( پردازنده های سیگنال دیجیتال ، FPGA ، ASIC ) بخش ممکن است توسط سخت افزار پشتیبانی نشود ، بنابراین باید از آن اجتناب شود. انتخاب کردن

هنگام اجرای الگوریتم با استفاده از حساب نقطه ثابت ، انتخاب ثابت است



کاربرد [ ویرایش ]
کاربرد اصلی روش شرایطی است که تقریب با مقادیر ویژه پیدا شود و یکی نیاز به پیدا کردن بردار ویژه تقریبی داشته باشد. در چنین شرایطی تکرار معکوس اصلی ترین و احتمالاً تنها روش استفاده است.
روشهای یافتن مقادیر ویژه تقریبی [ ویرایش ]
به طور معمول ، این روش در ترکیب با روش دیگری مورد استفاده قرار می گیرد که مقادیر ویژه تقریبی را پیدا می کند: مثال استاندارد الگوریتم مقادیر ویژه مقطعی است ، مثال دیگر تکرار ضریب ریلی است که در واقع همان تکرار معکوس با انتخاب مقادیر ویژه تقریبی است ضریب ریلی مربوط به بردار بدست آمده در مرحله قبلی تکرار است.
برخی شرایط وجود دارد که روش می تواند به تنهایی مورد استفاده قرار گیرد ، اما کاملاً حاشیه ای است.
نرمال ماتریس به عنوان تقریب با مقدار ویژه غالب [ ویرایش ]
ارزش ویژه غالب را می توان به راحتی برای هر ماتریسی تخمین زد. برای هر هنجار القایی این درست است

برآورد براساس آمار [ ویرایش ]
در برخی از برنامه های زمان واقعی ، لازم است بردارهای ویژه ماتریس هایی با سرعت میلیون ها ماتریس در ثانیه پیدا شود. در چنین برنامه هایی ، به طور معمول آمار ماتریس ها از قبل مشخص است و می توان برای مقادیر ویژه تقریبی ، مقادیر ویژه تقریبی ویژه برخی از نمونه های ماتریس بزرگ را در نظر گرفت. بهتر است ، کسي بتواند نسبت متوسط مقادير ويژه به رديف يا هنجار ماتريس را محاسبه كرده و ميانگين ارزش ويژه را به عنوان رديف يا هنجار ضرب در ميانگين مقدار آن نسبت تخمين بزند. بدیهی است که چنین روشی تنها با صلاحدید و تنها در مواردی که دقت بالا از اهمیت بالایی برخوردار نباشد ، قابل استفاده است. این روش تخمین یک مقدار ویژه را می توان با روشهای دیگر ترکیب کرد تا از خطای بیش از حد بزرگ جلوگیری شود.
منابع
https://en.wikipedia.org/wiki/Inverse_iteration
در ریاضیات ، تکرار توان (که به آن روش قدرت نیز گفته می شود ) یک الگوریتم ارزش ویژه است : با توجه به ماتریس مورب 





تکرار نیرو یک الگوریتم بسیار ساده است ، اما ممکن است به آرامی همگرا شود. وقت گیرترین کار الگوریتم ضرب ماتریس است
فهرست
روش [ ویرایش ]
انیمیشنی که الگوریتم تکرار توان را در ماتریس 2x2 تجسم می کند. ماتریس توسط دو بردار ویژه آن به تصویر کشیده شده است. خطا به عنوان محاسبه می شود
الگوریتم تکرار توان با بردار شروع می شود 
بنابراین ، در هر تکرار ، بردار 

اگر فرض کنیم 


بدون دو فرض بالا ، توالی 

جایی که 





با ارزش ویژه غالب همگرا می شود (با ضریب ریلی ). [ توضیحات لازم است ]
یکی می تواند این را با الگوریتم زیر محاسبه کند (در پایتون با NumPy نشان داده شده است):
#! / usr / bin / env python3
وارد کردن numpy به عنوان np
دف power_iteration ( ، num_simulations : INT ): # در حالت ایده آل را انتخاب نمایید یک بردار تصادفی # برای کاهش شانس است که بردار # متعامد به بردارهای ویژه است b_k = NP . تصادفی . رند ( . شکل [ 1 ])
for _ in range ( num_simulations ):
# محاسبه محصول ماتریس توسط بردار Ab
b_k1 = np . نقطه ( A ، b_k )
# محاسبه هنجار
b_k1_norm = np . linalg . هنجار ( b_k1 )
# بردار
b_k = b_k1 / b_k1_norm را عادی کنید
بازگشت b_k
power_iteration ( NP . آرایه ([[ 0.5 ، 0.5 ]، [ 0.2 ، 0.8 ]])، 10 )
بردار 
این الگوریتم برای محاسبه Google PageRank استفاده می شود .
از این روش می توان برای محاسبه شعاع طیفی (مقدار ویژه با بیشترین اندازه برای ماتریس مربع) با محاسبه ضریب Rayleigh استفاده کرد.
تحلیل [ ویرایش ]
اجازه دهید 







![{\ displaystyle [\ lambda _ {1}] ،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f3c83a8bae265cd5523c330d3b5f9901fee6ab0)


با فرض ، 

رابطه عود محاسباتی مفید برای
که در آن عبارت: 
عبارت فوق ساده به صورت
این حد از این واقعیت حاصل می شود که مقدار ویژه از 
نتیجه می شود که:
با استفاده از این واقعیت ، 

جایی که 

تسلسل و توالی 


متناوباً ، اگر A قابل مورب باشد ، اثبات زیر همان نتیجه را دارد
اجازه دهید λ 1 ، λ 2 ، ...، λ متر باشد متر مقادیر ویژه (شمارش، با تعدد) از و اجازه دهید V 1 ، V 2 ، ...، V متر باشد بردارهای ویژه مربوطه. فرض کنید که


بردار اولیه 
اگر 
از سوی دیگر:
از این رو، 

جایی که 
برنامه ها [ ویرایش ]
اگرچه روش تکرار نیرو فقط یک مقدار ویژه از یک ماتریس را تقریب می زند ، اما برای برخی از مشکلات محاسباتی همچنان مفید است . به عنوان مثال ، Google از آن برای محاسبه اسناد PageRank در موتور جستجوی خود استفاده می کند [2] و توییتر از آن برای نشان دادن توصیه های کاربران به دنبال استفاده از آنها استفاده می کند. [3] روش تکرار توان به ویژه برای ماتریس های پراکنده ، مانند ماتریس وب ، یا به عنوان روش بدون ماتریس که نیازی به ذخیره ماتریس ضریب نیست ، مناسب است.

برخی از الگوریتم های پیشرفته ارزش ویژه پیشرفته تر را می توان به عنوان تغییرات تکرار توان درک کرد. به عنوان مثال ، روش تکرار معکوس تکرار توان را به ماتریس اعمال می کند

منبع
https://en.wikipedia.org/wiki/Power_iteration
تکرار ضریب ریلی یک الگوریتم ارزش ویژه است که ایده تکرار معکوس را با استفاده از ضریب ریلی برای بدست آوردن برآورد دقیق تر از ارزش ویژه گسترش می دهد .
تکرار ضریب ریلی یک روش تکراری است ، یعنی توالی از راه حل های تقریبی را ارائه می دهد که در یک حد واقعی به یک محلول واقعی همگرا می شوند . همگرایی بسیار سریع تضمین شده است و برای به دست آوردن تقریب منطقی در عمل بیش از چند تکرار لازم نیست. ریلی خارج قسمت تکرار الگوریتم همگرا cubically برای هرمیتی یا متقارن ماتریس، با توجه به بردار اولیه این است که به اندازه کافی نزدیک به یک بردار ویژه از ماتریس است که در حال تجزیه و تحلیل.
فهرست
الگوریتم [ ویرایش ]
الگوریتم شباهت زیادی به تکرار معکوس دارد ، اما مقدار ویژه برآورد شده در پایان هر تکرار را با ضریب ریلی جایگزین می کند. با انتخاب مقداری شروع کنید


تقریب بعدی بردار ویژه را محاسبه کنید 
جایی که 
برای محاسبه بیش از یک مقدار ویژه ، الگوریتم را می توان با یک روش تورم ترکیب کرد.
توجه داشته باشید که برای مشکلات بسیار کوچک ، جایگزینی ماتریس معکوس با مواد افزودنی مفید است ، که همان تکرار را ارائه می دهد زیرا برابر با معکوس تا مقیاس بی ربط است (معکوس تعیین کننده ، به طور خاص). صحیح محاسبه صریح از معکوس آسان تر است (اگرچه معکوس برای بردارهایی برای مسائلی که کوچک نیستند نیز به راحتی قابل استفاده است) ، و از نظر عددی کاملاً صحیح است زیرا به عنوان همگرایی مقدار ویژه به خوبی تعریف می شود.
مثال [ ویرایش ]
ماتریس را در نظر بگیرید
که مقادیر ویژه دقیق آن است 


![v_ {2} = \ چپ [{\ start {matrix} 1 \\ - \ varphi \\ 1 \\\ end {matrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f214dbe77c8e1a2e8115416b0933c3f26a92a12e)
![v_ {3} = \ چپ [{\ start {matrix} 1 \\ 0 \\ 1 \\\ end {matrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc3ee9506136cc3a5c0c1828eb695ed4a0a93d3a)
(جایی که 
بزرگترین ارزش ویژه است
ما با حدس اولیه ارزش ویژه از شروع می کنیم
![b_ {0} = \ left [{\ start {matrix} 1 \\ 1 \\ 1 \\\ end {matrix}} \ right]، ~ \ mu _ {0} = 200](https://wikimedia.org/api/rest_v1/media/math/render/svg/94e8b5982dd8f14b9671a20b7b1691f1efb7a04c)
سپس ، تکرار اول بازده دارد
تکرار دوم ،
و سوم ،
که از آن همگرایی مکعبی مشهود است.
اجرای اکتاو
function x = rayleigh(A, epsilon, mu, x)
x = x / norm(x);
% the backslash operator in Octave solves a linear system
y = (A - mu * eye(rows(A))) \ x;
lambda = y' * x;
mu = mu + 1 / lambda
err = norm(y - lambda * x) / norm(y)
while err > epsilon
x = y / norm(y);
y = (A - mu * eye(rows(A))) \ x;
lambda = y' * x;
mu = mu + 1 / lambda
err = norm(y - lambda * x) / norm(y)
end
endمنبع
https://en.wikipedia.org/wiki/Rayleigh_quotient_iteration
از ویکیپدیا، دانشنامه آزاد
در ریاضیات ، در خارج قسمت رایلی [1] برای یک مجموعه داده ماتریس هرمیتی M و غیر صفر بردار X است تعریف می شود: [2] [3]
برای ماتریس ها و بردارهای واقعی ، شرایط هرمیتی بودن به متقارن بودن کاهش می یابد و مزدوج جابجا می شود 






برای بدست آوردن مقادیر دقیق تمام مقادیر ویژه از ضریب Rayleigh در قضیه min-max استفاده می شود . همچنین برای بدست آوردن تقریب مقدار ویژه از تقریب بردار ویژه در الگوریتم های ارزش ویژه (مانند تکرار ضریب Rayleigh ) استفاده می شود.
دامنه ضریب Rayleigh (برای هر ماتریسی ، نه لزوماً Hermitian) یک محدوده عددی نامیده می شود و شامل طیف آن است . وقتی ماتریس هرمیتی باشد ، محدوده عددی برابر با هنجار طیفی است. هنوز در تجزیه و تحلیل عملکرد ،
در مکانیک کوانتوم ، ضریب Rayleigh مقدار انتظار قابل مشاهده مربوط به عملگر M را برای سیستمی که حالت آن با x داده می شود ، می دهد .
اگر ماتریس پیچیده M را برطرف کنیم ، پس از آن نقشه مقدار ریلی (که تابعی از x در نظر گرفته می شود ) M را از طریق هویت قطبش کاملاً تعیین می کند . در واقع ، این درست می ماند حتی اگر اجازه دهیم M غیر هرمیتی باشد. (با این حال، اگر ما محدود زمینه اسکالرهای به اعداد حقیقی، سپس خارج قسمت رایلی تنها تعیین متقارن بخشی از M .)
فهرست
- 1مرزهایی برای هرمیتیان
- 2مورد خاص ماتریس کوواریانس
- 3در نظریه استورم-لیوویل استفاده کنید
- 4تعمیم ها
- 5همچنین ببینید
- 6منابع
- 7بیشتر خواندن
مرزهایی برای هرمیتیان  [ ویرایش ]
[ ویرایش ]
همانطور که در مقدمه بیان شد ، برای هر بردار x ، یکی دارد![R (M ، x) \ در \ چپ [\ lambda _ {\ min} ، \ lambda _ {\ max} \ راست]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3367126b01f5e7829818dc7726de621c12767dd3)


جایی که 




این واقعیت که ضریب یک میانگین وزنی از مقادیر ویژه است می تواند برای شناسایی مقادیر ویژه دوم ، سوم ، ... استفاده شود. اجازه دهید







مورد خاص ماتریس کوواریانس [ ویرایش ]
یک ماتریس کوواریانس تجربی 




اول اینکه مقادیر ویژه است 
ثانیاً ، بردارهای ویژه 
اگر مقادیر ویژه متفاوت باشد - در صورت تعدد ، می توان اساس را متعامد کرد.
برای اینکه ثابت کنید که ضریب ریلی توسط بردار ویژه با بیشترین مقدار ویژه به حداکثر می رسد ، تجزیه یک بردار دلخواه را در نظر بگیرید 

جایی که
مختصات است 

که، به orthonormality از بردارهای ویژه، می شود:
آخرین نمایش مشخص می کند که ضریب ریلی مجموع کسینوس های مربع زاویه های تشکیل شده توسط بردار است 

اگر بردار باشد 





تعریف کردن: 



بنابراین ، ضریب ریلی توسط بردار ویژه با بیشترین مقدار ویژه به حداکثر می رسد.
فرمول بندی با استفاده از ضریب لاگرانژ [ ویرایش ]
متناوباً ، با روش ضرب لاگرانژ می توان به این نتیجه رسید . قسمت اول نشان می دهد که مقدار تحت ثابت مقیاس بندی ثابت است

به دلیل این عدم تحقق ، مطالعه مورد خاص کافی است 

منوط به محدودیت 
جایی که 

و
بنابراین ، بردارهای ویژه 



استفاده در نظریه استورم-لیوویل [ ویرایش ]
نظریه Sturm – Liouville مربوط به عملکرد عملگر خطی است
در فضای محصول داخلی تعریف شده توسط
توابع راضی برخی شرایط مرزی مشخص در a و b . در این حالت ضریب ریلی است
این گاهی اوقات به شکل معادل ارائه می شود که با جداسازی انتگرال در عدد و استفاده از ادغام توسط قطعات بدست می آید :
تعمیم [ ویرایش ]
- برای یک جفت داده شده ( A ، B ) از ماتریس ها ، و یک بردار غیر صفر داده شده x ، ضریب تعمیم یافته ریلی به این صورت تعریف شده است:
مقدار رایلی تعمیم یافته ریلی را می توان به مقدار ریلی کاهش داد
از طریق تحول
جایی که
است تجزیه Cholesky از هرمیتی ماتریس مثبت معین B .
- برای یک جفت داده شده ( x ، y ) بردارهای غیر صفر و ماتریس Hermitian داده شده H ، ضریب تعمیم یافته ریلی را می توان به این صورت تعریف کرد:
که با R ( H ، x ) همزمان می شود وقتی x = y . در مکانیک کوانتوم ، این کمیت را "عنصر ماتریس" یا گاهی "دامنه انتقال" می نامند.
منبع
https://en.wikipedia.org/wiki/Rayleigh_quotient
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 |
SECT(2,0,0,-2) طیف گراف
بردارهای ویژه:
| 1 |
| 1 |
| 1 |
| 1 |
| 1- |
| 1 |
| 0 |
| 0 |
| 0 |
| 0 |
| -1 |
| 1 |
| 1- |
| 1- |
| 1 |
| 1 |
ساختار جبری → نظریه گروه نظریه گروه
نمایش
مفاهیم اساسی
نمایش
گروههای محدود
نمایش گروه های گسسته مشبک
نمایش
گروه های توپولوژیک و لی
نمایش
گروه های جبری
گروه های لی
نمایش
گروه های کلاسیک
نمایش
گروه های ساده لی
نمایش
سایر گروه های لی
نمایش
جبرها را لی بگویید
نمایش
جبر لی نیمه ساده
نمایش
نظریه بازنمایی
نمایش
گروه های لی در فیزیک
نمایش
دانشمندان واژه نامه جدول گروه های لی
در ریاضیات ، گروه خطی عمومی درجه n مجموعه ای از n × n ماتریس های معکوس پذیر ، همراه با عملکرد ضرب ماتریس معمولی است . این یک گروه را تشکیل می دهد ، زیرا محصول دو ماتریس معکوس پذیر دوباره معکوس پذیراست و وارون یک ماتریس وارون معکوس پذیراست ، ماتریس هویت به عنوان عنصر هویت گروه است. این گروه به این دلیل نامگذاری شده است که ستونهای یک ماتریس معکوس پذیر به طور خطی مستقل هستند ، از این رو بردارها / نقاطی که تعریف می کنند به صورت کلی خطی هستند، و ماتریسها در گروه خطی عمومی امتیازات را در حالت خطی کلی به نقاط در حالت خطی کلی می گیرند.
برای دقیق تر ، لازم است مشخص شود که چه نوع اشیایی ممکن است در ورودی های ماتریس ظاهر شوند. به عنوان مثال ، گروه خطی کلی روی از R (مجموعه اعداد حقیقی ) گروهی از n × n ماتریس های معکوس پذیر اعداد حقیقی است و با GL n ( R ) یا GL ( n ، R ) نشان داده می شود .
به طور کلی ، گروه خطی عمومی درجه n روی از هر میدان F (مانند اعداد مختلط ) ، یا یک حلقه R (مانند حلقه اعداد صحیح ) ، مجموعه ای از n × n ماتریس های معکوس پذیر با ورودی های F است (یا R ) ، دوباره با ضرب ماتریس به عنوان عملکرد گروه. [1] علامت گذاری معمول GL n ( F ) یا GL ( n ، F ) است یا اگر میدان قابل فهم باشد به سادگی GL ( n ) است.
به طور کلی هنوز ، گروه خطی کلی فضای بردار GL ( V ) گروه خود شکل گرایی انتزاعی است ، لزوماً به عنوان ماتریس نوشته نشده است.
گروه خطی ویژه ، نوشته شده SL ( N ، F ) یا SL N ( F )، است زیر گروه از GL ( N ، F ) متشکل از ماتریس با تعیین ، از مجموع 1
گروه GL ( n ، F ) و زیرگروههای آن اغلب گروههای خطی یا گروههای ماتریسی نامیده می شوند (گروه انتزاعی GL ( V ) یک گروه خطی است اما یک گروه ماتریسی نیست). این گروه ها در تئوری نمایش های گروهی مهم هستند و همچنین در مطالعه تقارن فضایی و تقارن فضاهای برداری به طور کلی و همچنین مطالعه چند جمله ای ها بوجود می آیند . گروه های مدولار ممکن است به عنوان خارج قسمت از گروه خطی ویژه متوجه SL (2، Z ) .
اگر n ≥ 2 باشد ، گروه GL ( n ، F ) هابلی نیست .
فهرست1گروه خطی عمومی یک فضای بردار2از نظر عوامل تعیین کننده3به عنوان یک گروه لی3.1مورد حقیقی3.2مورد مختلط4روی از زمینه های محدود4.1تاریخ5گروه خطی ویژه6زیر گروه های دیگر6.1زیر گروه های قطری6.2گروه های کلاسیک7گروههای مرتبط و مونوئیدها7.1گروه خطی مصوری7.2گروه وابسته7.3گروه نیمه خطی عمومی7.4مونوئید خطی کامل8گروه خطی عمومی بی نهایت9همچنین ببینید10یادداشت11لینک های خارجی
گروه خطی عمومی یک فضای برداری [ ویرایش ]
اگر V یک فضای بردار روی از میدان F باشد ، گروه خطی کلی V ، نوشته شده GL ( V ) یا Aut ( V ) ، گروه تمام اتومورفیسم های V است ، یعنی مجموعه تمام تبدیلات خطی ذهنی V → V ، همراه با ترکیب عملکردی به عنوان عملکرد گروه. اگر V دارای بعد محدود n باشد ، GL ( V ) و GL ( n ، F ) ناهمسان هستند . ایزومورفیسم متعارف نیست ؛ بستگی به انتخاب مبنا در V دارد . با توجه به اساس ( E 1 ، ...، E N ) از V و های automorphism T در GL ( V )، ما و سپس برای هر اساس بردار الکترونیکی من که
{\ displaystyle Te_ {i} = \ sum _ {j = 1} ^ {n} a_ {ij} e_ {j}}
برای برخی از ثابت IJ در F ؛ ماتریس مربوط به T پس از آن فقط ماتریس با ورودی های داده شده توسط a ij است .
به روشی مشابه ، برای یک حلقه جابجایی R ممکن است گروه GL ( n ، R ) به عنوان گروه خود شکل گیری یک ماژول R آزاد M از رتبه n تفسیر شود . همچنین می توان GL ( M ) را برای هر R- modul تعریف کرد ، اما به طور کلی این برای GL ( n ، R ) (برای هر n ) غیر همسان نیست .
از نظر عوامل تعیین کننده [ ویرایش ]
روی از یک میدان F ، ماتریس معکوس پذیر است اگر و فقط اگر تعیین کننده آن غیر صفر باشد. بنابراین ، یک تعریف جایگزین از GL ( n ، F ) به عنوان گروه ماتریس هایی با تعیین کننده غیر صفر است.
روی از یک حلقه مبادله R ، احتیاط بیشتری لازم است: یک ماتریس روی از R معکوس پذیراست اگر و فقط اگر تعیین کننده آن یک واحد در R باشد ، یعنی اگر تعیین کننده آن در R معکوس پذیرباشد . بنابراین ، ممکن است GL ( n ، R ) به عنوان گروهی از ماتریس ها تعیین شود که تعیین کننده های آنها واحد هستند.
روی از یک حلقه R غیر تغییر دهنده ، عوامل تعیین کننده اصلاً رفتار خوبی ندارند. در این مورد، GL
( N ، R ) ممکن است به عنوان تعریف گروه واحد از حلقه ماتریس M ( N ، R ) .
به عنوان یک گروه لی [ ویرایش ]
مورد حقیقی [ ویرایش ]
گروه خطی کلی GL ( n ، R ) در قسمت اعداد حقیقی یک گروه لی حقیقی از بعد n 2 است . برای دیدن این نکته ، توجه داشته باشید که مجموعه تمام n × n ماتریس حقیقی ، M n ( R ) ، یک فضای برداری حقیقی از بعد n 2 را تشکیل می دهد . زیرمجموعه GL ( n ، R ) از آن ماتریسهایی تشکیل شده است که تعیین کننده آنها غیر صفر است. عامل تعیین کننده یک نقشه چند جمله ای است و از این رو GL ( n ،R ) یک زیرگروه اشتیانی باز از M n ( R ) است ( زیرمجموعه باز غیر خالی M n ( R ) در توپولوژی زاریسکی ) ، و بنابراین [2] یک منیفولد صاف از همان بعد است.
جبر لی از GL ( N ، R ) ، نشان داده می شود{\ displaystyle {\ mathfrak {gl}} _ {n} ،} شامل همه n × n ماتریس حقیقی است که کموتاتور به عنوان براکت Lie عمل می کند.
به عنوان یک چند برابر، GL ( N ، R ) است متصل بلکه دو اجزای متصل : ماتریس با تعیین مثبت و کسانی که با تعیین منفی است. م componentلفه هویت ، نشان داده شده با GL + ( n ، R ) ، متشکل از ماتریس های حقیقی n × n با تعیین کننده مثبت است. این نیز یک گروه Lie از بعد n 2 است . جبر لی همان GL ( n ، R ) است .
گروه GL ( n ، R ) نیز غیرتراکمی است . "این" [3] حداکثر زیر گروه فشرده از GL ( N ، R ) است گروه متعامد O ( N )، در حالی که «" زیر گروه فشرده حداکثر GL + ( N ، R ) است گروه متعامد ویژه SO ( N ). در مورد SO ( n ) ، گروه GL + ( n ، R ) به سادگی متصل نیست(به استثنای n = 1) ، بلکه دارای یک گروه بنیادی غیر همسان با Z برای n = 2 یا Z 2 برای n > 2 است .
مورد مختلط [ ویرایش ]
گروه خطی عمومی روی از زمینه اعداد مختلط ، GL ( N ، C ) ، یک است مختلط لی گروه از ابعاد مختلط N 2 . به عنوان یک گروه لی حقیقی (از طریق تحقق) ، بعد 2 n 2 دارد . مجموعه تمام ماتریس های حقیقی یک زیر گروه حقیقی Lie را تشکیل می دهد. اینها با مطالب مطابقت دارد
GL ( n ، R ) n ، C ) 2n ، R ) ،
که دارای ابعاد حقیقی n 2 ، 2 n 2 و 4 n 2 = (2 n ) 2 هستند . مجتمع N ماتریس بعدی می تواند به عنوان حقیقی 2 مشخص N ماتریس بعدی که حفظ یک ساختار مختلط خطی - مشخص، که رفت و آمد با یک ماتریس J به طوری که J 2 = - من ، که در آن J مربوط به ضرب واحد موهومی من .
جبر لی مربوط به GL ( N ، C ) عبارت است از تمام N × N ماتریس مختلط با کموتاتور خدمت به عنوان براکت لی.
برخلاف حالت حقیقی ، GL ( n ، C ) به هم متصل است . این امر به دنبال، در بخش، از گروه ضربی از اعداد مختلط C * متصل است. منیفولد گروه GL ( n ، C ) فشرده نیست. بلکه حداکثر زیر گروه فشرده آن گروه واحد U ( n ) است. همانطور که برای U ( n ) ، منیفولد گروه GL ( n ، C ) به سادگی متصل نیست اما دارای یک گروه بنیادی غیر همسان با Z است .
روی از زمینه های محدود [ ویرایش ]
جدول Cayley از GL (2 ، 2) ، که با S 3 نامتقارن است .
اگر F یک میدان محدود با عناصر q باشد ، بنابراین ما گاهی اوقات به جای GL ( n ، F ) GL ( n ، q ) را می نویسیم . وقتی ص اول است، GL ( N ، P ) است گروه automorphism بیرونی از گروه Z ص N ، و همچنین های automorphism گروه زیرا، Z ص N آبلی است، به طوری که گروه automorphism داخلی بی اهمیت است.
ترتیب GL ( n ، q ) :
{\ displaystyle \ prod _ {k = 0} ^ {n-1} (q ^ {n} -q ^ {k}) = (q ^ {n} -1) (q ^ {n} -q) ( q ^ {n} -q ^ {2}) \ \ cdots \ (q ^ {n} -q ^ {n-1}).}
این را می توان با شمردن ستونهای احتمالی ماتریس نشان داد: ستون اول می تواند چیزی به جز بردار صفر باشد. ستون دوم می تواند چیزی به جز مضرب ستون اول باشد. و به طور کلی، ک هفتم ستون می تواند هر بردار نه در طول خطی از اولین K - 1 ستون. در علامت گذاری آنالوگ q ، این است{\ displaystyle [n] _ {q}! (q-1) ^ {n} q ^ {n \ را انتخاب کنید 2}} .
به عنوان مثال ، GL (3 ، 2) دارای نظم (8 - 1) (8 - 2) (8 - 4) = 168 است . این گروه اتومورفیسم هواپیمای Fano و از گروه Z 2 3 است و همچنین به عنوان PSL شناخته می شود (2 ، 7) .
به طور کلی ، می توان نقاط Grassmannian را نسبت به F شمرد : به عبارت دیگر تعداد زیر فضاهای یک بعد مشخص k . این فقط مستلزم یافتن ترتیب زیرگروه تثبیت کننده یکی از چنین فضاهای زیر و تقسیم به فرمولی است که توسط قضیه تثبیت کننده مدار ارائه شده است .
این فرمول به متصل تجزیه شوبرت از Grassmannian، و س -analogs از اعداد بتی از Grassmannians مختلط است. این یکی از سرنخ های منتهی به حدس های ویل بود .
توجه داشته باشید که در حد q ↦ 1 ترتیب GL ( n ، q ) به 0 می رسد! - اما تحت روش صحیح (تقسیم بر ( س - 1) N ) ما می بینیم که آن منظور از گروه متقارن (مقاله را ببینید Lorscheid) است - در فلسفه از زمینه با یک عنصر ، یک نتیجه تفسیر گروه متقارن به عنوان گروه خطی کلی روی میدان با یک عنصر: S n ≅ GL ( n ، 1) .
تاریخچه [ ویرایش ]
گروه خطی عمومی در یک زمینه اصلی ، GL ( ν ، p ) ، ساخته شد و ترتیب آن توسط Évariste Galois در سال 1832 ، در آخرین نامه خود (به شوالیر) و دوم (از سه) نسخه خطی پیوست محاسبه شد ، که وی در زمینه مطالعه گروه Galois از معادله عمومی نظم p ν . [4]
گروه خطی ویژه [ ویرایش ]
مقاله اصلی: گروه خطی ویژه
گروه خطی ویژه ، SL ( n ، F ) ، گروهی از تمام ماتریس ها با تعیین کننده 1 است. آنها از این نظر خاص هستند که روی یک زیرمجموعه قرار می گیرند - آنها یک معادله چند جمله ای را برآورده می کنند (همانطور که تعیین کننده چند جمله ای در ورودی ها است). ماتریس های این نوع گروهی را تشکیل می دهند به عنوان تعیین کننده حاصلضرب دو ماتریس محصول تعیین کننده های هر ماتریس است. SL ( N ، F ) است زیر گروه نرمال از GL ( N ، F ) .
اگر ما ارسال F × برای گروه ضربی از F (به استثنای 0)، پس از آن تعیین شده است همریخت گروه
DET: GL ( N ، F ) → F × .
که صوری است و هسته آن گروه خطی خاصی است. لذا با اولین قضیه ریخت ، GL ( N ، F ) / SL ( N ، F ) است ریخت به F × . در واقع ، GL ( n ، F ) را می توان به عنوان یک محصول نیمه مستقیم نوشت :
GL ( N ، F ) = SL ( N ، F ) ⋊ F ×
گروه خطی ویژه نیز گروه مشتق شده (همچنین به عنوان زیر گروه کموتاتور شناخته می شود) GL ( n ، F ) (برای یک میدان یا حلقه تقسیم F ) به شرطی که{\ displaystyle n \ neq 2} یا k این زمینه با دو عنصر نیست . [5]
هنگامی که F است R و یا C ، SL ( N ، F ) است زیر گروه لی از GL ( N ، F ) از ابعاد N 2 1 - . جبر لی از SL ( N ، F ) عبارت است از تمام N × N ماتریس روی از F با اضمحلال اثری . براکت Lie توسط کموتاتور داده می شود .
ویژه گروه خطی SL ( N ، R ) می تواند به عنوان گروهی از مشخص حجم و گرایش حفظ تبدیلهای خطی R N .
گروه SL ( n ، C ) به سادگی متصل است ، در حالی که SL ( n ، R ) متصل نیست. SL ( n ، R ) همان گروه بنیادی GL + ( n ، R ) را دارد ، یعنی Z برای n = 2 و Z 2 برای n > 2 .
زیرگروههای دیگر [ ویرایش ]
زیرگروههای قطری [ ویرایش ]
مجموعه تمام ماتریس های قطری معکوس پذیر ، یک زیر گروه GL ( n ، F ) ناهمسان از ( F × ) n را تشکیل می دهد . در زمینه هایی مانند R و C ، اینها مطابق با نجات فضا هستند. به اصطلاح اتساع و انقباض
ماتریس عددی یک ماتریس قطری است که ثابت برابر است ماتریس . مجموعه ای از تمام غیر صفر ماتریس اسکالر به شکل یک زیر گروه از GL ( N ، F ) ریخت به F × . این گروه است مرکز از GL ( N ، F ) . به طور خاص ، این یک زیر گروه طبیعی و عادی است.
مرکز SL ( N ، F ) است که به سادگی مجموعه ای از تمام ماتریس اسکالر با واحد تعیین کننده، و ریخت به گروه است N هفتم ریشه های وحدت در زمینه F .
گروه های کلاسیک [ ویرایش ]
گروههای به اصطلاح کلاسیک زیرگروههای GL ( V ) هستند که نوعی شکل دو خطی را در فضای بردار V حفظ می کنند . اینها شاملگروه متعامد ، O ( V ) ، که فرم درجه دوم غیر منحط را در V حفظ می کند ،گروه متقارن ، Sp ( V ) ، که فرم متقارن را در V (یک فرم متناوب غیر منحط) حفظ می کند ،گروه واحد ، U ( V ) ، که وقتی F = C باشد ، یک فرم ازادگر غیر خراب در V را حفظ می کند .
این گروه ها نمونه های مهمی از گروه های لی را ارائه می دهند.
گروهها و مونوئیدهای مرتبط [ ویرایش ]
گروه خطی مصوری [ ویرایش ]
مقاله اصلی: گروه خطی پیش فرض
تصویری گروه خطی PGL ( N ، F ) و ویژه تصویری خطی گروه PSL ( N ، F ) هستند خارج قسمت از GL ( N ، F ) و SL ( N ، F ) توسط خود مراکز (که از تقسیم عددی بر مضرب از تشکیل ماتریس هویت در آن) آنها کنش القا شده در فضای تصویری مرتبط هستند .
گروه وابسته [ ویرایش ]
مقاله اصلی: گروه Affine
گروه affine به AFF ( N ، F ) یک IS پسوند از GL ( N ، F ) توسط گروهی از ترجمه در F N . می توان آن را به عنوان یک محصول نیمه مستقیم نوشت :
Aff ( n ، F ) = GL ( n ، F ) ⋉ F n
که در آن GL ( n ، F ) به صورت طبیعی بر روی F n عمل می کند . گروه آیفین را می توان به عنوان گروهی از تمام تغییر شکل های آیفین فضای آفرین زیربنای فضای بردار F n مشاهده کرد .
یکی ساختارهای مشابهی برای سایر زیر گروه های گروه خطی عمومی دارد: به عنوان مثال ، گروه ویژه وابسته زیرگروه تعریف شده توسط محصول نیمه مستقیم ، SL ( n ، F ) ⋉ F n است و گروه Poincare گروه وابسته ای است که به گروه لورنتس ، O (1 ، 3 ، F ) ⋉ F n .
گروه نیمه خطی عمومی [ ویرایش ]
مقاله اصلی: گروه نیمه خطی عمومی
گروه عمومی semilinear ΓL ( N ، F ) گروه از همه است invertible تبدیلاتsemilinear ، و شامل GL. تحول نیمه خطی تحولی است که به صورت خطی "تا یک پیچ و تاب" است ، به معنی "تا یک شکل دهی درست در یک ضرب اسکالر". می توان آن را به عنوان یک محصول نیمه مستقیم نوشت:
ΓL ( n ، F ) = Gal ( F ) ⋉ GL ( n ، F )
جایی که Gal ( F ) گروه Galois از F (روی از میدان اصلی آن ) است ، که با عمل Galois در ورودی ها بر روی GL ( n ، F ) عمل می کند.
علاقه اصلی ΓL ( N ، F ) است که در ارتباط تصویری گروه semilinear PΓL ( N ، F ) (که شامل PGL ( N ، F )) است گروه collineation از فضای تصویری ، برای N > 2 ، و نقشه در نتیجه semilinear مورد توجه هندسه فرافکنی هستند .
مونوئید خطی کامل [ ویرایش ]
این بخش نیاز به توسعه با: خواص اساسی دارد. با افزودن به آن می توانید کمک کنید . ( آوریل 2015 )
اگر یکی حذف محدودیت تعیین بودن غیر صفر، ساختار جبری ناشی است مونوئید ، معمولا به نام مونوئید کامل خطی ، [6] [7] [8] اما گاهی اوقات نیز کامل خطی نیم گروه ، [9] مونوئید خطی عمومی [10] [11] و غیره در واقع یک نیم گروه معمولی است . [7]
گروه خطی عمومی بی نهایت [ ویرایش ]
گروه کلی خطی بی نهایت و یا پایدار گروه کلی خطی است حد مستقیم از اجزاء GL ( N ، F ) → GL ( N + 1، F ) به عنوان بالا سمت چپ بلوک ماتریس . این یا با GL ( F ) یا با GL (∞ ، F ) مشخص می شود ، و همچنین می تواند به عنوان ماتریس های بی نهایت وارون قابل تفسیر باشد که فقط در بسیاری از مکان ها با ماتریس هویت متفاوت است. [12]
این در تئوری K جبری برای تعریف K 1 استفاده می شود ، و به لطف تناوب Bott ، از یک توپولوژی برتر برخوردار است .
این نباید با فضای اپراتورهای معکوس پذیر (محدود) در فضای هیلبرت ، که یک گروه بزرگتر است ، و از نظر توپولوژیکی بسیار ساده تر ، یعنی انقباضی ، اشتباه گرفته شود - به قضیه کوپر مراجعه کنید .
همچنین به [ ویرایش ] مراجعه کنید
لیست گروههای ساده متناهیSL 2 ( R )تئوری بازنمایی SL 2 ( R )نمایندگی گروه های لی کلاسیک
خلاصه کردن
توضیحات فوق ابتدایی ترین ایده GCN است که فرم تبدیل فوریه هسته کانولوشن را تغییر می دهد . ساختار GCN در بسیاری از مقالات بر اساس ایده های فوق الذکر با برخی تحولات ساده ریاضی است. پس از درک مطالب فوق ، می توانید به "همه چیز به همان ترتیب تغییر می کند" برسید.
اتصال محلی و اشتراک پارامتر در GCN
دو ایده اصلی در CNN وجود دارد: اتصال شبکه محلی و به اشتراک گذاری پارامترهای هسته کانولوشن.
پس نمی توانیم کمک کنیم اما فکر نکنیم: این دو نکته در GCN چیست؟ ساختار گراف شکل زیر را به عنوان مثال برای کاوش در نظر بگیرید

اتصال محلی در GCN
(الف) اگر از GCN نسل اول استفاده شود ، مطابق فرمول(36)هسته کانولوشن است

در این زمان می توان دریافت که این هسته کانولوشن خاصیت محلی ندارد ، زیرا در همه موقعیت ها عناصر غیر صفر وجود دارد. با توجه به مثال اولین راس ، اگر رابطه محلی مرتبه اول در نظر گرفته شود ، اولین ردیف در هسته کانولوشن فقط باید داشته باشد[1،1]،[1،2]،[1،5]عناصر موجود در این سه موقعیت غیر صفر هستند. به عبارت دیگر ، این یک هسته پیچشی کاملاً متصل به یکدیگر است.
طبق نسل دوم ، اگر نسل دوم GCN باشد(40)چه زمانیک=1هسته محصول است

چه زمانی ک=2هسته کانولوشن است

با نگاهی به ساختار همجواری نمودار ، عناصر غیر صفر هسته کانولوشن همه در موقعیت محلی سازی هستند.
اشتراک پارامتر در GCN
خلاصه کردن
ماهیت عمل کانولوشن گسسته در تصویر ، جمع وزنی است و ماهیت عمل روی نمودار نیز جمع وزنی است ؛ و معنای فیزیکی کانولوشن گسسته در تصویر استخراج خصوصیات مختلف است " باندهای فرکانسی "از تصویر. ، و معنای فیزیکی آن در نمودارسود پس از ایجاد تغییرات کوچک در همه گره های همسایه (از ماتریس لاپلاس) برای یک راس بدست آمده استلحاصل جمع هر ردیف صفر است و عبارت جمع کردن روی نمودار را می توان مشاهده کرد)
GCN دیگر
در مورد مشکل نمودارهای هدایت شده
توضیحات قبلی درمورد GCN نمودارهای بدون جهت است . اگر یک مسئله نمودار جهت دار باشد ، بیشترین تفاوت در این است که ماتریس مجاورت به یک ماتریس نامتقارن تبدیل خواهد شد. در این زمان ، ماتریس Lapley و تجزیه طیفی آن (Laplace ماتریس خود بر روی نمودار بدون جهت تعریف شده است). در حال حاضر برای حل مشکل دو راه وجود دارد.
(الف) رابطه همسایگی نمودار را برای حفظ تقارن دوباره تعریف کنید
به عنوان مثال ، MotifNet: یک شبکه مبتنی بر نقش و نگار Graph Convolutional برای نمودارهای جهت دار پیشنهاد می کند از Graph Motifs برای تعریف روابط همسایگی نمودار استفاده کنید.
(B) روش محاسبه GCN را با استفاده از ماتریس Lapley دور بزنید
درباره پردازش ویژگی لبه
بیشتر آنها برای ویژگی گره پردازش می شوند و اگر می خواهید ویژگی edge را پردازش کنید ، مقاله THOMAS KIPF را بررسی کنید
شک
- ترجمه در CNN تغییر شکل داده نشده است
- چه رابطه ای بین تبدیل لاپلاس (مشتق مرتبه دوم) و تبدیل فوریه وجود دارد؟ چرا می توان از عملکرد مشخصه تبدیل لاپلاس به عنوان مبنای تبدیل فوریه استفاده کرد؟
- هر دو تبدیل فوریه معکوس در نمودار و قضیه جمع آوری در نمودار فاقد اشتقاق هستند
- معنی فرکانس روی نمودار و رابطه بین مقادیر ویژه
- فرمول(36)که درایکسمعنای خاص
- معنای فیزیکی کانولوشن در نمودار
- فرمول عود چبیشف
- چرا تبدیل فوریه هسته کانولوشن ماتریس است و آیا نباید بردار باشد؟
https://zdaiot.com/MachineLearning/%E5%9B%BE%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/%E5%9B%BE%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/
استفاده از چند جمله ای Chebyshev برای محاسبه بازگشتی هسته کانولوشن
در GCN نسل دوم ، ل آره n×n ماتریس ، بنابراینلج محاسبه هنوز است ای(n2)پیچیده ، موجهای موجود در نمودارها از طریق تئوری نمودار طیفی ، روشی را برای متناسب کردن هسته کانولوشن با استفاده از چند جمله ای چبیشف برای کاهش پیچیدگی محاسبات پیشنهاد می کند. هسته همگراییgθ(Λ)می توان آن را با چند جمله ای تغییر شکل داده شده Chebyshev تقریبی کرد. (در اصل ، ما باید به دنبال تقریب چند جمله ای Minimax باشیم ، اما نویسنده گفت که استفاده مستقیم از چند جمله ای Chebyshev نیز بسیار موثر است)
(42)gθ(Λ)≈Σک=0ک-1βکتیک(Λ~)
βآRکیک بردار چبیشف را نشان می دهد ،βک آیا ضریب (مقیاس) چند جمله ای چبیشف است.تیک(Λ~) گرفتن است Λ~=2Λ/λمترآایکس-منچند جمله ای چبیشف ، دلیل این تغییر شکل این است که ورودی چند جمله ای چبیشف باید در باشد[-1،1] بین.
از خواص چند جمله ای چبیشف ، فرمول عود زیر را می توان بدست آورد
(43)تیک(Λ~)ایکس=2Λ~تیک-1(Λ~)ایکس-تیک-2(Λ~)ایکس(44)تی0(Λ~)=من،تی1(Λ~)=Λ~
در میان آنها ، ایکس تعریف همان است که در بالا ، استn بردار بعدی از ویژگی های هر راس تشکیل شده است (البته می تواند باشدn*مترماتریس ویژگی ، و سپس هر راس دارد مترویژگی ها ، امامترمعمولا خیلی کوچکتر ازn )
در حال حاضر یافتن آن دشوار نیست:(42)دیگر هیچ محصولی ماتریسی در محاسبه وجود ندارد ، شما فقط باید محصولی از ماتریس و بردار را محاسبه کنید. یک بار محاسبه کنیدتیک(Λ~)ایکسپیچیدگی این استای(|E|) ،Eآیا مجموعه ای از لبه ها در نمودار است ، بنابراین پیچیدگی کل عملیات استای(ک|E|). وقتی Graph یک نمودار پراکنده است ، شتاب محاسبه به ویژه واضح است و پیچیدگی در این زمان بسیار کمتر ازای(n2)
تیک(Λ~)آره Λازک چند جمله ای را سفارش دهید ، وتوتوتی=من،بنابراین باید
(45)توΛ~کتوتی=توΛ~توتی...توΛ~توتی⏞ک=(توΛ~توتی)ک=(تو(2Λλمترآایکس-من)توتی)ک=(تو2Λλمترآایکستوتی-تومنتوتی)ک=(2λمترآایکستوΛتوتی-من)ک=(2λمترآایکسل-من)ک=ل~ک
در میان آنها ، ل~=2λمترآایکسل-من .
کترتیب چند جمله ای را ترتیب دهید:f(ایکس،θ)=Σک=0کایکسکθک=φ(ایکس)تیθ، در میان آنهاφ(ایکس)=[1،ایکس،ایکس2،...،ایکسک]تیآRک+1،θ=[θ0،...،θک]تیآRک+1.
دیده می شود که برایک چند جمله ای را سفارش دهیدتیک(Λ~)درکماتریس ضرب سمت چپتوماتریس ضرب راستتوتیهمه مربوط بهک چند جمله ای را سفارش دهیدتیک(ل~)درکاصطلاح ، بنابراین می توانید فرمول ترکیب نمودار را دریافت کنید:
(46)gθ(Λ)*ایکس≈توΣک=0کβکتیک(Λ~)توتیایکس=Σک=0کβکتوتیک(Λ~)توتیایکس=Σک=0کβکتیک(ل~)ایکس
https://zdaiot.com/MachineLearning/%E5%9B%BE%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/%E5%9B%BE%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/
نمودار نمودار در یادگیری عمیق
ترکیب نمودار در یادگیری عمیق به طور مستقیم با فرمول تجمعی نمودار که در بخش 6 به دست آمده بسیار متفاوت است ، اما هرگز تغییر نمی کند.(31)فرمول منبع مشتق است.
محتوای بخش 1 بسیار واضح توضیح داده شده است: ترکیب در یادگیری عمیق طراحی هسته با پارامترهای اشتراکی قابل آموزش است ، از(31)فرمول بسیار شهودی به نظر می رسد: پارامتر کانولوشن در کانولوشن نمودار است دمنآg(ساعت^(λمن)).
نسل اول GCN
در شبکه های طیفی و شبکه های متصل محلی در نمودارها ، به سادگی و تقریباًدمنآg(ساعت^(λمن))به هسته ای تبدیل می شوددمنآg(θمن)، کدام است:
(36)yایتوتیپتوتی=σ(توgθ(Λ)توتیایکس)
در میان آنها ،gθ(Λ)=(θ1⋱θn)
فرمول(36)این لایه در GCN نسل اول استاندارد است ، جایی کهσ(⋅)آیا تابع فعال سازی است ،Θ=(θ1،θ2،...،θn)دقیقاً مانند وزن در شبکه عصبی سه لایه ، یک پارامتر دلخواه است که با مقداردهی اولیه مقدار و سپس با استفاده از انتشار برگشت خطا تنظیم می شود.ایکساین بردار ویژگی مربوط به هر راس روی نمودار است (بردار متشکل از ویژگی های استخراج شده از یک مجموعه داده ویژه).
روش پارامتر نسل اول دارای اشکالاتی است: به طور عمده:
(1) هر تبلیغ رو به جلو باید محاسبه شود تو،دمنآg(θمن) وتوتیمحصول ماتریسی این سه ، به ویژه برای نمودارهای در مقیاس بزرگ ، هزینه محاسباتی بالاتری دارد که در مقاله استای(n2)پیچیدگی محاسباتی
(2) محلی سازی مکانی هسته کانولوشن خوب نیست (این بیشتر در بخش 9 توضیح داده شده است)
(3) هسته هسته همگراییnمولفه های
به دلیل نقایص فوق ، طراحی هسته کانولوشن نسل دوم به وجود آمد.
نسل دوم GCN
( شبکه های عصبی همگرایی در نمودارها با فیلتر طیفی سریع موضعی ) ، قرار دهیدساعت^(λمن)هوشمندانه طراحی شده است Σج=0کαجλمنج(تعریف اصلی این است:ساعت^(λمن)=Σمن=1نساعت(من)تومن*(من)) ، که:
(37)yایتوتیپتوتی=σ(توgθ(Λ)توتیایکس)
در میان آنها ،gθ(Λ)=(Σج=0کαجλ1ج⋱Σج=0کαجλnج)
به نظر می رسد فرمول فوق غیرقابل تشخیص است ، بنابراین با تبدیل آن با ضرب ماتریس نگاهی به آن می اندازیم.
(38)(Σج=0کαجλ1ج⋱Σج=0کαجλnج)=Σج=0کαجΛج
در میان آنها ،Λماتریس مورب است ، و عناصر مورب هستندλ1،λ2،...،λn، وΛجاین همچنین یک ماتریس مورب است و هر عنصر استλ1،λ2،...،λnازجقدرت. و جلوΣج=0کαجیک ثابت است ، نتیجه ضرب این دو ثابت ضرب شده در هر مقدار ماتریس است ، بنابراین برابر است با سمت چپ.
سپس می توانید صادرات انجام دهید:
(39)توΣج=0کαجΛجتوتی=Σج=0کαجتوΛجتوتی=Σج=0کαجلج
فرمول فوق به این دلیل ایجاد شده استل2=توΛتوتیتوΛتوتی=توΛ2توتی و توتیتو=E، که می تواند به گسترش یابدلجمورد.
تعریف هر نماد همان تعریف بخش 5 است.
فرمول(37)تبدیل می شود:
(40)yایتوتیپتوتی=σ(Σج=0کαجلجایکس)
در میان آنها(α1،α2،...،αک) این یک پارامتر دلخواه است که با انتساب اولیه و سپس با استفاده از انتشار خطا تنظیم می شود.لجماتریسلازجقدرت.
فرمول(40)مزایای هسته کانولوشن طراحی شده عبارتند از:
(1) هسته کانولوشن فقط داردکپارامترها ، به طور کلی کخیلی کوچکتر از n، پیچیدگی پارامترها بسیار کاهش می یابد.
(2) پس از تحول ماتریس ، به طرز جادویی مشخص شد که نیازی به تجزیه ویژه نیست و ماتریس لاپلاسی مستقیماً استفاده می شودلتحول ایجاد کنید. اما به دلیل محاسبهلج، پیچیدگی محاسباتی هنوز وجود داردای(n2)
(3) هسته کانولوشن محلی سازی فضایی خوبی دارد ، به ویژه ،کاین یک میدان پذیرای هسته کانولوشن است ، به این معنی که هر کانولوشن یک جمع وزنی از ویژگی های راس مرکزی همسایه K-hop را انجام می دهد و ضریب وزنαک
بصری تر ، _K_ = 1 به معنای انجام یک جمع وزنی از هر راس و ویژگی همسایه مرتبه اول آن است ، همانطور که در شکل زیر نشان داده شده است:

توضیح: چون کیک=1وقتی ، قسمت کانولوشن برابر است باαلایکس، و ازلبه شکل ماتریس ، مشاهده می شود که ماتریس لاپلاس فقط در استمرکزراس و راس مرتبه اول متصل (همسایه 1 هاپی) عناصر غیر صفر دارند و بقیه صفر هستند. بنابراین ، معادل انجام یک جمع وزنی از هر راس و ویژگی های همسایه مرتبه اول آن است و بنابراین توانایی درک محلی را دارد.علاوه بر این ، مجموع هر ردیف از ماتریس لاپلاس 0 است و عناصر مورب با مجموع عناصر باقیمانده در همان ردیف برابر است. این ماهیت جمع آوری را در نمودار نشان می دهد: یک راس انجام می شود در تمام گره های مجاور سود حاصل پس از یک تغییر کوچک.از آنجا که پارامترهایی در کانولوشن وجود داردαبنابراین می توان با تبلیغ عقب محاسبه کردلضریب در هیچ چیزی توضیح نمی دهد ، فقط مهم نیست که چه شکلی از ضرب وجود داردαموقعیت عنصر 0 همیشه عنصر 0 است.
به طور مشابه ، وضعیت _K_ = 2 در شکل زیر نشان داده شده است:

شرح:
(41)ل+ل2=[8-511-50-515-62-601-68-62112-615-7-5-5-62-7151001-513]
بنابراین، هنگامی کهک=2وقتی ، قسمت کانولوشن برابر است با(Σج=02αجلجایکس)از بالال+ل2ملاحظه می شود که فقط رئوس آن و رئوس متصل مرتبه دوم (همسایه 2-هاپ) عناصر غیر صفر دارند و بقیه صفر هستند. بنابراین ، معادل انجام یک جمع وزنی از هر راس و ویژگی همسایه مرتبه دوم آن است و همچنین توانایی درک محلی را دارد. از آنجا که پارامترهایی در کانولوشن وجود داردαبنابراین می توان با تبلیغ عقب محاسبه کردل+ل2ضریب در هیچ چیزی توضیح نمی دهد ، فقط مهم نیست که چه شکلی از ضرب وجود داردαموقعیت عنصر 0 همیشه عنصر 0 است.
شکل بالا فقط یک راس را به عنوان مثال در نظر می گیرد.هر ترکیب GCN عملیاتی را که در شکل روی همه رئوس نشان داده شده است کامل می کند. تجمع فضایی به این معنی است که گره روی نمودار فقط با نقاط مجاور توزین می شود ، اما بحث اصلی در اینجا بحث پیچیدگی طیفی است ، که در فضای طیفی نمودار غیرمستقیم کانولوشن است. سیگنال بردار طول n است و فیلتر نیز بردار طول n است.
چگونه می توان فرکانس مقادیر ویژه ماتریس لاپلاس را درک کرد
مفهوم "فرکانس" را نمی توان بصورت تصویری در فضای نمودار نمایش داد ، بنابراین درک انتزاعی از معادله ویژه است .
ماتریس لاپلاسیل ازnمقادیر ویژه غیر منفی واقعی، در جهت صعودی ازλ1≤λ2≤...≤λn ، و کوچکترین ارزش ویژهλ1=0،زیراnمقدار ویژه مربوط به بردار همه یک بعد 0 است.
اگرچه بردارهای ویژه ماتریس منحصر به فرد نیستند ، اما مقادیر ویژه منحصر به فرد هستند. این بدان معناست که اگرچه بردارهای ویژه ما با یکدیگر متعامد هستند لزوماً حاوی همه 1 بردار نیستند ، اما مقادیر ویژه ماتریس باید مقادیر ویژه مربوط به هر 1 بردار را داشته باشد.
ثابت كردن:
لبه عنوان ... تعریف شده استل=د-آ، در میان آنهادماتریس درجه است ، هر عنصر ازدمن=Σج=1nآمنج. وآاین ماتریس مجاورت است ، زیرا ما در اینجا در مورد یک نمودار ساده بحث می کنیم ، یعنی هیچ ارتباطی بین خود و خود وجود ندارد ، بنابراین مورب 0 است. دیده می شود کهلحاصل جمع هر ردیف 0 است. بنابراین می توانید:
(34)ل(11⋮1)=0→
اثبات شده
دیده می شود که مقادیر ویژه ماتریس لاپلاسیλ1=0در آن زمان ، هر م componentلفه بردار ویژه ثابت است و دامنه تغییر آن 0 است ؛ ما آن را بدون اثبات می دهیم ، هرچه مقدار ویژه متغیر باشد به دامنه تغییر هر یک از اجزای بردار ویژه مربوط می شود. در سیگنال کلی تبدیل فوریه ، اساس این استه-جwتی، یکی از آنهاwمی تواند فرکانس را نشان دهد ،wهرچه بزرگتر ، سریعتر تغییر پایه می یابد. تشبیه به تبدیل فوریه نمودار ، مقدار ویژه فرکانس را نشان می دهد ، مقدار ویژه بزرگتر ، پایهتومنسریعتر تغییر.
از درک ریاضی معادله ویژه:
(35)لتو=λتو
تعیین شده توسط نمودارnدر فضای بعدی ، مقدار ویژه کوچکتر استλمننمایش: ماتریس لاپلاسلپایه مربوطهتومنهرچه م theلفه و "اطلاعات" در قسمت بالا کمتر باشد ، البته قسمت کم فرکانس نیز قابل چشم پوشی است.
در حقیقت ، فشرده سازی تصویر یک اصل است ، در آن تجزیه ماتریس پیکسل ها ، مقادیر ویژه کوچک (فرکانس پایین) همه 0 می شوند ، کاهش بعد PCA یکسان است ، پس از تجزیه ماتریس کوواریانس در آن ، قبل از حذف نزولی بردارهای اختصاصی مربوط به مقادیر ویژه K به عنوان "محور مختصات" جدید استفاده می شود.
نظریه Graph Convolution به پایان رسیده است ، بیایید Grav Convolution Network را شروع کنیم
منبع
https://zdaiot.com/MachineLearning/%E5%9B%BE%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/%E5%9B%BE%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/
انحراف عمومی
بر اساس موارد فوق ، از قیاس قضیه کانولوشن برای گسترش عملیات کانولوشن به نمودار استفاده کنید.
قضیه کانولوشن: تبدیل فوریه کانولوشن تابع محصول تابع تبدیل فوریه است ، یعنی برای تابع f(تی) در مقابلساعت(تی)جمع این دو تبدیل معکوس محصول تبدیل فوریه عملکرد آن است:
(29)f*ساعت=F-1[f^(ω)ساعت^(ω)]=12Π∫f^(ω)ساعت^(ω)همنωتیدω
تشبیه به نمودار و تعریف تبدیل فوریه را وارد کنید ، fبا هسته کانولوشنساعت جمع بندی در نمودار را می توان به شرح زیر محاسبه کرد:
fتبدیل فوریه است f^=توتیf
هسته همگراییساعتتبدیل فوریه به صورت ماتریس مورب نوشته شده است:
در این میان ، هسته پیوند است * مطابق با نیاز طراحی شده استساعت(اندازه استن×1) تبدیل فوریه در نمودار. اینجاتوتیgکل به عنوان یک هسته تجمع قابل یادگیری در نظر گرفته می شود .
محصول تبدیل فوریه این دو است:(ساعت^(λ1)⋱ساعت^(λn))توتیf
ضربدرتوتبدیل معکوس حاصل از محصول دو تبدیل فوریه را پیدا کنید ، سپس ترکیب را پیدا کنید:
جایی که: تووتوتیتعریف همان تعریف در بخش 5 است
توجه: فرمول تجمیع نمودار در بسیاری از مقالات به شرح زیر است:
(32)(f*ساعت)G=تو((توتیساعت)⊙(توتیf))
⊙محصول hadamad را نشان می دهد. برای دو بردار ، این عمل محصول داخلی است ؛ برای دو ماتریس با ابعاد یکسان ، عملکرد محصول عناصر مربوطه است.
در حقیقت ، معادله (31) و معادله (32) دقیقاً یکسان هستند.
زیرا (ساعت^(λ1)⋱ساعت^(λn))در مقابل توتیساعتهمه ساعت تبدیل فوریه در نمودار
طبق قوانین ضرب ماتریس: ماتریس مورب (ساعت^(λ1)⋱ساعت^(λn))در مقابل توتیf مجموع محصولاتتوتیساعت در مقابل توتیfعملکرد محصول عناصر مربوطه دقیقاً یکسان است.
در اینجا به طور عمده فشار دهید(31)فرمول این است که با یادگیری عمیق زیر ترکیب شود.
این قسمت از نظریه احساس می کند که فاقد ادله اثبات دقیق است و بیشتر آنها مطابق مفهوم قیاس تبلیغ می شوند. به عنوان مثال ، چه رابطه ای بین تبدیل لاپلاس (مشتق مرتبه دوم) و تبدیل فوریه وجود دارد؟ چرا می توان از عملکرد مشخصه تبدیل لاپلاس به عنوان مبنای تبدیل فوریه استفاده کرد؟ هر دو تبدیل فوریه معکوس در نمودار و قضیه جمع آوری در نمودار فاقد اشتقاق هستند. اکنون فقط یک معرفی کوتاه از ایده ها ارائه می دهم و جزئیات خاص باید در آینده مورد مطالعه قرار گیرند.
چرا می توان از بردار ویژه ماتریس لاپلاس به عنوان مبنای تبدیل فوریه استفاده کرد؟ مقدار مشخصه فرکانس را نشان می دهد؟
چرا می توان از بردار ویژه ماتریس لاپلاس به عنوان مبنای تبدیل فوریه استفاده کرد؟
درک اساسی تغییر شکل فوریه بیان هر عملکرد به عنوان ترکیبی خطی از چندین عملکرد متعامد (متشکل از گناه ، کاس) است.

از بخش ششم به سبک چینی عبور کنید(28)همچنین می توان مشاهده کرد که تبدیل فوریه نمودار نیز هر بردار تعریف شده روی نمودار را می گیردf، بیان شده به عنوان یک ترکیب خطی از بردارهای ویژه ماتریس لاپلاس ، یعنی:
(33)f=f^(λ1)تو1+f^(λ2)تو2+...+f^(λn)توn
بنابراین : چرا هر بردار روی نمودارfآیا می توان همه را چنین ترکیبی خطی بیان کرد؟
دلیلش این هست که(تو1→،تو2→،...،توn→)روی نمودار استnدر فضای بعدیnیک بردار متعامد مستقل خطی (به همین دلیل خصوصیات ماتریس لاپلاس را در بخش 5 ببینید) ، که می تواند از دانش جبر خطی شناخته شود:nفضای بعدیnیک بردار مستقل خطی می تواند مجموعه ای از مبانی را در فضا تشکیل دهد ، و بردار ویژه ماتریس لاپلاسی نیز مجموعه ای از مبنای متعادل است .
به طور مشابه ، تبدیل سنتی فوریه معکوس فرکانس استωانتگرال:
(25)F-1[F(ω)]=12Π∫F(ω)همنωتیدω
مهاجرت به نمودار به یک جفت ارزش ویژه تبدیل می شودλمنجمع بندی:
(26)f(من)=Σمن=1نf^(λمن)تومن(من)
برای گسترش تبدیل فوریه معکوس از شکل نمودار به ماتریس از ضرب ماتریس استفاده کنید:
(27)(f(1)f(2)⋮f(ن))=( تو1(1)تو2(1)...تون(1)تو1(2)تو2(2)...تون(2)⋮⋮⋱⋮تو1(ن)تو2(ن)...تون(ن))(f^(λ1)f^(λ2)⋮f^(λن))
که هستfفرم ماتریسی تبدیل معکوس فوریه در نمودار است:
(28)f=توf^
جایی که: توتعریف همان تعریف در بخش 5 است.fباf^هر دو هستندن×1بردار ستون.
دیدگاه ریاضی
ماتریس لاپلاسی دارای برخی از خواص خوب به شرح زیر است:
- ماتریس لاپلاسین یک ماتریس متقارن است ، که می تواند توسط آن تعیین شوددباآ(نمودارهای بدون جهت) از ماتریس های متقارن مشتق شده اند. ماتریس متقارن باید داشته باشدnدو بردار ویژه مستقل خطی ، بردارهای ویژه نسبت به یکدیگر متعامد هستند ، یعنی ماتریس تشکیل شده توسط همه بردارهای خاص یک ماتریس متعامد است. بنابراین ، نمودارnمقدار هر راس تجزیه شده توسط ماده (تجزیه طیفی) است که مربوط به حوزه طیفی GCN است.
- ماتریس لاپلاس فقط در است مرکزرأس با عناصر غیر صفر به رأس مرتبه اول (همسایه 1 هاپی) متصل است و بقیه صفر هستند
- از آنجا که ماتریس لاپلاس یک ماتریس متقارن است ، تمام مقادیر ویژه آن اعداد واقعی هستند.

این تعریف را با استفاده از ماتریس لاپلاس به راحتی می توان به شرح زیر بدست آورد:
- ماتریس لاپلاس نیمه قطعی مثبت است و n مقادیر ویژه واقعی مربوطه بزرگتر یا برابر با 0 هستند ، یعنی0=λ1≤λ2≤...≤λn، و کوچکترین مقدار ویژه 0 است که به راحتی از ویژگی 3 بدست می آید.
تجزیه طیفی ماتریس لاپلاس (تجزیه ویژه)
هسته اصلی GCN بر اساس تجزیه طیفی ماتریس لاپلاس است. ادبیات در مورد این قسمت از مطالب توضیح زیادی نمی دهد. مبتدیان ممکن است با سو mis تفاهمات زیادی روبرو شوند ، بنابراین ابتدا تجزیه ویژه را درک کنید.
تجزیه طیفی ، تجزیه ویژه و مورب سازی یک ماتریس همه مفهوم یکسانی هستند ( تجزیه ویژه _ 百度 文库).
همه ماتریس ها نمی توانند از هم جدا شوند ، شرایط لازم و کافی وجود داردnماتریس مربع وجود داردnیک بردار ویژگی خطی مستقل.
با این حال ، ماتریس لاپلاس یک ماتریس متقارن نیمه قطعی مثبت است (ماتریس قطعی نیمه مثبت خود یک ماتریس متقارن است ، ماتریس مشخص نیمه مثبت _ 百度 文库، که در اینجا برای مطابقت با خصوصیات زیر نوشته شده است ، برای جلوگیری از سردرگمی) ، دارای سه ویژگی زیر است:
- ماتریس متقارن باید دارای n بردار ویژه خطی مستقل باشد
- مقدار ویژه ماتریس نیمه قطعی مثبت باید غیر منفی باشد
- بردارهای ویژه ماتریس نسبت به یکدیگر متعامد هستند ، یعنی ماتریس تشکیل شده توسط همه بردارهای خاص یک ماتریس متعامد است.
از مطالب فوق می توان فهمید که ماتریس لاپلاس باید طیفی تجزیه شود و بعد از تجزیه فرم خاصی دارد.
برای ماتریس لاپلاس ، تجزیه طیفی آن:
(14)ل=تو(λ1⋱λn)تو-1
در میان آنهاT=(T1→،T2→،...،Tn→)، آیا ماتریس با بردار ستون به عنوان واحد بردار ویژه است ، به عبارت دیگرتومن→آیا بردار ستون واحد است .
(λ1⋱λn) آرهnآرایه مورب مقادیر ویژه.
به واسطه توماتریس متعامد ، یعنی توتوتی=E
بنابراین تجزیه ویژگی را می توان به صورت زیر نوشت:
این فرمول آخرین موردی است که در ادبیات به دست آمده است ، اما سو mis تفاهم نکنید ، درست ترین ترکیب ادبی معکوس ماتریس ویژه است. فقط خصوصیات ماتریس لاپلاس را می توان به عنوان ترانسپوز ماتریس اختصاصی نوشت.
در واقع ، از مطالب بالا می توان فهمید: کل مشتق از بسیاری از خصوصیات ریاضی استفاده می کند ، و من اینجا آن را با جزئیات بیشتر می نویسم تا از درک اشتباه همه جلوگیری کند.
تبدیل و جمع شدن فوریه را محبوب کنید
با انتقال انتقال فوریه و تبدیل سنتی به نمودار ، کار اصلی در واقع انتقال عملکرد مشخصه عملگر Laplacian استه-منωتیاین تبدیل به بردار ویژه ماتریس لاپلاسی متناظر با نمودار می شود .
تبدیل فوریه تعمیم یافته
خوانندگانی که می خواهید آن را شخصا قادر به خواندن در حال ظهور درست از پردازش سیگنال در نمودار ها: گسترش تجزیه و تحلیل داده ها با ابعاد بالا به شبکه های دیگر و نامنظم دامنه . موارد زیر درک و پالایش من این است:
تبدیل فوریه بر روی نمودار
تبدیل سنتی فوریه به این صورت تعریف می شود:
(16)F(ω)=F[f(تی)]=∫f(تی)ه-منωتیدتی
علامتf(تی)با توابع پایهه-منωتیامتیازات ، پس چرا باید جستجو کرده-منωتیبه عنوان یک تابع پایه؟ از نظر ریاضی ،ه-منωتی لاپلاسین△عملکرد ویژه (رضایت معادله ویژه) ، ω مربوط به مقدار مشخصه است.
معادله ویژه تعمیم یافته به شرح زیر است:
(17)آV=λV
در میان آنهاآ آیا یک تحول خطی است ،Vآیا عملکرد ویژه است (چه زمانیآوقتی ماتریس است ،Vآیا بردار ویژه است) ،λآیا مقدار مشخصه است.
ه-منωتیراضی باشید:
(18)Δه-منωتی=∂2∂تی2ه-منωتی=-ω2ه-منωتی
البتهه-منωتی تبدیل لاپلاسΔعملکرد مشخصه ، ωاین رابطه نزدیک به مقدار مشخصه دارد .
علاوه بر این ، با توجه به اینکه محصول داخلی به معنای گسترده نوعی فرافکنی است ، فرمول است(16)همچنین می توان آن را به عنوان محصول داخلی زیر نوشت:
(19)F(w)=〈f(تی)،هجwتی〉〈هجwتی،هجwتی〉
در اینجا هیچ مدرکی ارائه نشده است ، زیرا فعلاً فاصله ادغام را نمی دانم[-∞،∞]تعریف محصول داخلی عملکرد.
بنابراین ، می توانید به آن فکر کنید. هنگام پرداختن به مشکلات نمودار ، شما از ماتریس لاپلاس استفاده می کنید (ماتریس لاپلاس اپراتورهای گسسته Laplace هستند. اگر می خواهید بیشتر بدانید ، می توانید به اپراتور Discrete Laplace مراجعه کنید ) ، بنابراین به طور طبیعی به Laplace بروید ماتریس Plass
در حقیقت ، پس از تفکر عمیق در مورد تغییر فوریه قبل از این ، به این نتیجه رسیدیم که اصطلاحاً تبدیل فوریه تجزیه سیگنال حوزه زمان به مجموعه ای از اصول متعامد کامل است و فرمول(16)این ضریب است که به طور کامل متعامد تجزیه می شود. بنابراین با تعمیم دادن به قسمت نمودارها ، رئوس روی نمودار شبیه سیگنال های حوزه زمان ماست. اکنون ما باید یک مجموعه از اصول متعامد کامل را برای تجزیه آن پیدا کنیم ، و ماتریس لاپلاسnبردارهای مشخصه را می توان بر روی نمودار تشکیل دادnمجموعه ای از پایه های متعامد کامل در یک فضای ابعادی . پس از تجزیه ماتریس لاپلاس به دامنه طیفی ، می توانید از خصوصیاتی استفاده کنید که کانولوشن دامنه زمانی برابر با ضرب دامنه طیفی باشد. ابتدا ضرب را در دامنه طیفی تعریف کنید و سپس از تبدیل فوریه معکوس استفاده کنید تا در دامنه زمانه جمع شود. .
لآیا ماتریس لاپلاس است ، Vآیا بردار ویژه آن است که به طور طبیعی فرمول زیر را برآورده می کند
(20)لV=λV
انتگرال گسسته نوعی محصول داخلی است که از تبدیل فوریه تعریف شده در نمودار تقلید می کند
زیراتومن*این یک بردار ستون واحد است ، بنابراین مخرج 1 است ، که می تواند به صورت فرمول زیر نوشته شود.
(بیست و دو)F(λمن)=f^(λمن)=Σمن=1نf(من)تومن*(من)
fروی نمودار است نبردار بعدی ،f(i)مکاتبات یک به یک با رئوس نمودار ، تومن(من)اولین را نشان می دهدمناز بردارهای ویژهمنقطعات. سپس مقدار مشخصه (فرکانس)λiپایین،fتبدیل نمودار فوریه همان است λiبردار ویژگی مربوطه تومن عملیات داخلی ضرب را انجام دهید.
توجه: عملکرد ضرب داخلی فوق در فضای مختلط تعریف شده است ، بنابراینتومن*(من)، که بردار ویژگی استتومن的 مزدوج برای کسب اطلاعات بیشتر در مورد محصول Inner ، لطفا به فضای محصول Inner مراجعه کنید .
برای گسترش تبدیل فوریه در شکل نمودار به ماتریس از ضرب ماتریس استفاده کنید
که هست fفرم ماتریسی تبدیل فوریه در نمودار
جایی که: توتی تعریف همان تعریف در بخش 5 است.fباf^هر دو هستندن×1بردار ستون.
چرا از ماتریس لاپلاس استفاده می شود
موارد زیر برخی از درک من یا در اینترنت است. البته ، به معنای دقیق ، ماتریس لاپلاس با استنباط دقیق ریاضی و اثبات در GCN اعمال می شود.
معنای جسمی
برای کاوش در معنای فیزیکی ماتریس لاپلاسی ، باید از معادلات وی شروع شودل=د-آبه عنوان مثال ، توضیح دهید که چرا ماتریس لاپلاس اینگونه تعریف شده است.
تعریف ریاضی اپراتور Laplace به شرح زیر است:
(3)△=Σمنδ2δایکسمن2
مفهوم واضح است ، تعداد مشتقات جزئی مرتبه دوم غیر مخلوط و !
مشتق جزئی مخلوط: برای یک تابع باینری ، ابتدا مشتق متغیر اول را بدست آورید و سپس مشتق متغیر دوم را بگیرید تا مشتق جزئی مخلوط را بدست آورید. به جای مشتقات جزئی مختلط: مانند یک تابع باینری ، فقط برای یافتن مشتق جزئی دوم برای یک متغیر خاص.
باید فهمید که این تعریف دقیق ریاضی آن است ، و همه عملگرهای دیگر لاپلاسیایی مورد خاصی از آن هستند ، یا در برخی شرایط تقریبی هستند.
بیایید ابتدا به چگونگی تقریب تصویر نگاهی بیندازیم. تصویر نوعی داده گسسته است ، بنابراین لاپلاسین آن باید گسسته شود.
صحبت از تعریف مشتق
(4)f،(ایکس)=δf(ایکس)δایکس≈f(ایکس+1)-f(ایکس)
سپس:
(5)δ2f(ایکس)δایکس2=f"(ایکس)≈f،(ایکس)-f،(ایکس-1)≈f(ایکس+1)-f(ایکس)-(f(ایکس)-f(ایکس-1))=f(ایکس+1)+f(ایکس-1)-2f(ایکس)
نتیجه گیری 1: مشتق دوم تقریباً با اختلاف دوم آن برابر است.
نتیجه گیری 2: مشتق دوم برابر است با سود حاصل از اغتشاش در تمام درجات آزادی. درجه آزادی یک تابع یک بعدی را می توان 2 دانست که به ترتیب 1 و 1 جهت هستند.
برای یک تصویر دو بعدی ، دو جهت دارد (4 درجه آزادی) که می تواند تغییر کند ، یعنی اگر(ایکس،y)اغتشاش پیکسل در ، می توان آن را به چهار حالت تغییر داد،،،(ایکس+1،y)،(ایکس-1،y)،(ایکس،y+1)،(ایکس،y-1). البته ، اگر جهت مورب نیز به عنوان درجه ای از آزادی در نظر گرفته شود ، چندین حالت دیگر به آن اضافه می شود،،،(ایکس+1،y+1)،(ایکس+1،y-1)،(ایکس-1،y+1)،(ایکس-1،y-1)در واقع ، این دقیقاً همین امر در پردازش تصویر است. البته ، اگر فکر می کنید که ایجاد مزاحمت در پیکسل ممکن است به هر پیکسلی تبدیل شود ، در اینصورت درجه آزادی آن تعداد پیکسل های کل تصویر است (اما آیا این همچنان اغتشاش نامیده می شود؟). در حقیقت ، نتیجه گیری تقریباً یکسان است ، بیایید در مورد اولین مورد بحث کنیم.
(6)△=δ2f(ایکس،y)δایکس2+δ2f(ایکس،y)δy2≈f(ایکس+1،y)+f(ایکس-1،y)-2f(ایکس،y)+[f(ایکس،y+1)+f(ایکس،y-1)-2f(ایکس،y)]=f(ایکس+1،y)+f(ایکس-1،y)+f(ایکس،y+1)+f(ایکس،y-1)-4f(ایکس،y)
فرمول فوق را می توان به عنوان مقدار Laplacian در یک نقطه خاص از تصویر فهمید ، که این سود پس از ایجاد مزاحمت و تغییر آن به پیکسل های مجاور است.
عملگر Laplacian در پردازش تصویر به صورت ماتریس نوشته می شود ، که درک آن راحت تر است.
[0-10-14-10-10]
این به ما یک نتیجه گیری واضح می دهد: لاپلاس در پردازش تصویر ، سود حاصل از یک تغییر کوچک در تمام درجات آزادی در یک نقطه خاص است.
پس از بحث در مورد معنای فیزیکی لاپلاس روی تصویر ، ما به نمودار گسترش می یابیم و معنای فیزیکی لاپلاس روی نمودار را کاوش می کنیم.
سپس به Graph تعمیم دهید ، برایVنمودار یک گره ، اجازه دهید گره باشد 1،...،V، و ماتریس همجواری آن استآ.
درجه آزادی این نمودار چقدر است؟ جواب حداکثرV.
زیرا اگر نمودار یک نمودار کامل باشد ، یعنی بین هر دو گره یک لبه وجود داشته باشد ، یک گره را آشفته کنید ، ممکن است به هر گره تبدیل شود.
سپس عملکرد بالاfالبته این یکVبردار ابعاد ، یعنی:
(7)f=(f1،...،fV)
در میان آنهاfمنیعنی عملکردfدر گرهمنمقدار. تقلیدf(ایکس،y)به این معنا کهfکه در(ایکس،y)مقدار در.
برای هر گرهمناغتشاش را انجام دهید ، ممکن است به هر گره مجاور وی تبدیل شودجآنمن، در میان آنهانمنگره محله مرتبه اول گره i را نشان می دهد.
همانطور که در بالا نتیجه گرفتیم ، لاپلاسین سود کسب شده پس از تغییرات اندک در تمام درجات آزادی است.
اما برای Graph ، گره بردهمنتغییر به گرهجسود چیست؟ که هستfج-fمنقیمتش چنده؟ آسانترین چیزی که می توان به آن فکر کرد قدرت مرزی بین آنها است. سپس مانند آن رفتار کنیدآمنجدرست!
سپس ، برای گره i ، سود آن تغییر می کند Σجآنمنآمنج[fج-fمن]
بنابراین ، برای Graph ، Laplacian آن به شرح زیر است:
(8)(△f)من=Σمنδ2fδمن2≈Σجآنمنآمنج[fج-fمن]
در بالا جآنمنبه دلیل گره قابل حذف استمنباجاگر مستقیماً مجاور نباشند ،آمنج=0؛
به ساده سازی ادامه دهید:
(9)Σجآنمنآمنج[fج-fمن]=Σجآمنجfج-Σجآمنجfمن=(آf)من-(دf)من=[(آ-د)f]من
که:
(10)(△f)من=[(آ-د)f]من
برای هرچیمنتاسیس شده است ، بنابراین:
(11)△f≡(آ-د)f
یعنی Laplacian روی نمودار باید به این صورت تعریف شودآ-د!
توجه: در بالا هیچ اشتقاق ریاضی دقیق وجود ندارد و حتی عبارات ریاضی نیز خیلی دقیق نیستند. این ماده عمدتا از قیاس + مشتق ساده گرفته شده است. من عمدتا می خواهم توضیح دهم که چرا عملگر لاپلاس روی نمودار چنین تعریف شده است. و چرا چنین استآ-دبجاید-آ، من کاملا نمی فهمم
درباره Laplacian نرمال متقارن :لsys=د-1/2لد-1/2=من-د-1/2آد-1/2. لاپلاسین ترکیبی را مشاهده کنیدلفرم ، می توانید ببینید که هر خطمنمجموع 0 است و بزرگترین عنصر آن استدمن، بنابراین استفاده کنیدلضرب ماتریس های مورب چپ و راستد-1/2معادل بالعادی سازی را انجام دهید. مزیت این کار جلوگیری از پراکندگی شیب یا انفجار شیب است . Laplacian نرمال پیاده روی تصادفی :لرw=د-1لهمین مسئله نیز صادق است.
ماتریس لاپلاس
تعاریف نمودار تحول فوریه و تجمع نمودار هر دو از ماتریس لاپلاسی نمودار استفاده می کنند ، بنابراین بیایید ابتدا ماتریس لاپلاسی را معرفی کنیم.
تعریف
برای یک نمودارG، ما به طور کلی از مجموعه امتیازات استفاده می کنیمVو مجموعه لبه هاEبرای توصیف کردن. به این معنا کهG(V،E). در میان آنهاVآیا همه نقاط در مجموعه داده های ما است(v1،v2،...vn). برایVهر دو نقطه داخل را می توان با یا بدون لبه متصل کرد. وزن را تعریف می کنیمآمنجبرای نکتهvمنو اشاره کنیدvجوزن بین اگر یک نمودار بدون جهت است ، پسآمنج=آجمن. برای دو نقطه که با یک لبه به هم متصل شده اندvمنباvج،آمنج>0، برای دو نقطه بدون لبه متصل شده استvمنباvج،آمنج=0. برای هر نقطه از نمودارvمن، درجه آندمنبه عنوان مجموع وزن تمام لبه های متصل به آن ، یعنی تعریف می شود
(1)دمن=Σج=1nآمنج
با استفاده از تعریف هر درجه ، می توانیم یکn×nماتریس درجهد، این یک ماتریس مورب است ، فقط مورب اصلی دارای مقداری است که مربوط به اول استمنخطمندرجه هر نقطه به شرح زیر تعریف می شود:
(2)د=(د1.........د2...⋮⋮⋱......دn)
با استفاده از مقادیر وزن بین تمام نقاط ، می توانیم ماتریس مجاورت نمودار را بدست آوریمآ، همچنین یکn×nماتریس ، اولین منخطج مقادیر با وزن ما مطابقت داردآمنج.
شکلGماتریس لاپلاس به این صورت تعریف شده استل=د-آ، در میان آنها ل آیا ماتریس لاپلاس است ،د آیا ماتریس درجه راس (ماتریس مورب) است ، عناصر مورب درجه هر راس به نوبه خود هستند ، آماتریس همجواری نمودار است. با مشاهده مثالی در شکل زیر ، می توانید به سرعت روش محاسبه ماتریس لاپلاس را درک کنید.

آنچه در اینجا می خواهم توضیح دهم این است كه در واقع سه ماتریس لاپلاكسی معمولاً استفاده می شود:
شماره 1 ل=د-آنام حرفه ای تر ماتریس لاپلاسی تعریف شده Laplacian ترکیبی است . ماتریس متقارن است.
شماره 2 لsys=د-1/2لد-1/2=من-د-1/2آد-1/2تعریف Laplacian نرمال متقارن نامیده می شود ، که در بسیاری از مقالات GCN استفاده می شود. به عبارت دیگر ، ماتریس لاپلاسین یک ماتریس متقارن است و عناصر آن را می توان با فرمول زیر محاسبه کرد:

شماره 3 لرw=د-1لاین تعریف Rap Random normalized Laplacian نامیده می شود . برخی از خوانندگان اظهار داشتند که شباهت های Graf Convolution و Diffusion را مشاهده کرده اند . البته ، از Laplacian عادی تصادفی پیاده روی ، می توان فهمید که این دو شباهت دارند ( در واقع ، فقط یک ماتریس شباهت بین این دو. برای تبدیل ، می توانید به شبکه های عصبی Diffusion-Convolutional و شکل زیر مراجعه کنید). به عبارت دیگر ، ماتریس لاپلاسی یک ماتریس متقارن نیست و عناصر آن را می توان با فرمول زیر محاسبه کرد:

خوانندگانی که به محتوای مرتبط نیاز ندارند می توانند از این بخش بگذرند

در حقیقت ، تعریف ماتریس لاپلاس در ویکی پدیا کاملاً واضح است و فقط تعریف اول در برخی از مقدمه های داخلی وجود دارد . این باعث شد که در ابتدا در روند خواندن ادبیات کمی گیج شوم ، و من آن را ویژه نوشتم تا به شما کمک کند دوباره از مشکلات مشابه جلوگیری کنید.
دامنه طیفی
کانولوشن فضایی به طور شهودی مبتنی بر عملکرد کانولوشن در تصویر است ، اما فاقد مبانی نظری خاصی است. کانولوشن دامنه فرکانس متفاوت است. در مقایسه با چرخش دامنه فضایی ، برای تحقق بخشیدن به ترکیب ، عمدتا از تبدیل نمودار فوریه (نمودار تبدیل فوریه) استفاده می شود . به بیان ساده ، از ماتریس لاپلاسی نمودار استفاده می کند تا عملگر لاپلاسی را در دامنه فرکانس استخراج کند و سپس ترکیب را در فضای اقلیدسی در دامنه فرکانس آنالیز می کند تا فرمول جمع بندی نمودار را استخراج کند. اگرچه فرم فرمول بسیار شبیه به هم آمیختگی فضایی است ، اما فرایند استخراج از کانولوشن دامنه فرکانس تا حدودی دشوار و مبهم است.
دامنه طیفی اساس نظری GCN است. این نوع تفکر استفاده از تئوری نمودارها برای تحقق بخشیدن به عملیات چرخش بر روی نمودارهای توپولوژیک است. از منظر دوره زمانی کل تحقیق: ابتدا دانشمندانی که GSP (پردازش سیگنال نمودار) را مطالعه کردند ، تبدیل فوریه را بر روی نمودار تعریف کردند و سپس کانولوشن را بر روی نمودار تعریف کردند و در نهایت با آموزش عمیق پیشنهاد Graph Convolutional Network.
پس از مطالعه دقیق این مقاله ، یک سری س ofال باید به ذهن شما خطور کند:
Q1 طیفی (طیفی) چیست
طیف درک شخصی ارزش ویژه ماتریس لاپلاس است. همچنین در تجزیه و تحلیل عددی ، ماتریس آموخته شده استآn×nمقدار مشخصهλمن(من=1،2،...،n)، گفتρ(آ)=مترآایکس1≤من≤n|λمن|برایآشعاع طیفی ازآشعاع طیفی حداکثر مقدار ویژه آن است.
Q2 دامنه طیفی چیست؟
شخصاً درک کنید که دامنه طیفی یک ماتریس لاپلاس استnفضایی متشکل از بردارهای ویژگی خطی مستقل.
Q2 نظریه نمودار طیفی چیست؟
لطفاً برای نظریه نمودار طیفی به این مقاله مراجعه کنید. یک خلاصه ساده استفاده از مقادیر ویژه و بردارهای ویژه ماتریس لاپلاسی نمودار برای مطالعه خصوصیات نمودار است. از نظر شخصی ، این به معنای نگاشت دامنه فضایی نقشه توپولوژیک به حوزه طیفی است ، شبیه نقشه برداری تبدیل فوریه از دامنه زمان به دامنه فرکانس. روش اساسی تحول پایه (تجزیه) است .
Q3 چرا GCN از تئوری نمودار طیفی استفاده می کند؟
این باید س coreال اصلی باشد که من نمی توانم در طی خواندن مقاله آن را درک کنم. درک این س questionال نیاز به تعاریف و تعاریف ریاضی زیادی دارد و تسلط بر آن بدون یک پایه ریاضی خاص دشوار است (من خیلی ضعیف هستم برای یادگیری ، پاسخ دادن به این سوال دشوار است).
بنابراین ، ابتدا این مشکل را دور بزنید ، به آنچه نمودار Spectral بدست می آورد نگاه کنید و سپس چرا را کشف کنید؟
مشخصات وب
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.09132003030
موضوعات وب
- نظریه طیف گراف
- پرواز
- هندسه
- هسته ای
- ترکببات
- نمایش گروه
- سیستم های دینامیکی
- نظریه کد گذاری
- ریاضی فازی
- جبر پیشرفته
- توپولوژی
- معادلات دیفرانسیل
- مقاله ها
- سیستم عصبی
- آنالیز عددی
- آنالیزریاضی و آنالیز حقیقی
- توابع مختلط و کاربردها
- نظریه اعداد
- برنامه ریزی خطی و غیر خطی
- حل عددی معادلات دیفرانسیل
- نظریه مجموعه ها
- جبرخطی و جبرخطی عددی
- اقتصاد
- تاریخ ریاضی
- انسان شناسی وفلسفه ریاضی
- توپولوژی جبری
- هندسه جبری
- هندسه ریمانی و هندسه هذلوی
- بازی
- نقشه برداری دریایی
- گراف
- آمار غیرپارامتری
- نجوم
- منیفولد دیفرانسیل
- نظریه گروه
- نظریه حلقه
- نظریه مدول ها
- آمار و احتمال
- ریاضی 2
- فیزیک -ریاضی
- تحقیق
- ریاضی مهندسی
- درس ترمودینامیک و مکانیک آماری
- مکانیک تحلیلی
- برق یا فیزیک 2
- فیزیک مدرن
- کوانتم
- نسبیت
پیوندها
پیوندهای روزانه
آرشیو وب
- اسفند ۱۴۰۴
- بهمن ۱۴۰۴
- دی ۱۴۰۴
- آذر ۱۴۰۴
- آبان ۱۴۰۴
- شهریور ۱۴۰۴
- مرداد ۱۴۰۴
- خرداد ۱۴۰۴
- اردیبهشت ۱۴۰۴
- بهمن ۱۴۰۳
- دی ۱۴۰۳
- آذر ۱۴۰۳
- آبان ۱۴۰۳
- مهر ۱۴۰۳
- خرداد ۱۴۰۳
- اردیبهشت ۱۴۰۳
- فروردین ۱۴۰۳
- اسفند ۱۴۰۲
- بهمن ۱۴۰۲
- دی ۱۴۰۲
- آذر ۱۴۰۲
- آبان ۱۴۰۲
- مهر ۱۴۰۲
- تیر ۱۴۰۲
- خرداد ۱۴۰۲
- اردیبهشت ۱۴۰۲
- فروردین ۱۴۰۲
- اسفند ۱۴۰۱
- بهمن ۱۴۰۱
- دی ۱۴۰۱
- آبان ۱۴۰۱
- مهر ۱۴۰۱
- شهریور ۱۴۰۱
- مرداد ۱۴۰۱
- تیر ۱۴۰۱
- خرداد ۱۴۰۱
- آرشيو

















![{\ displaystyle \ left ({\ frac {1} {\ lambda _ {1}}} J \ right) ^ {k} = {\ start {bmatrix} [1] &&&& \\ & \ left ({\ frac { 1} {\ lambda _ {1}}} J_ {2} \ راست) ^ {k} &&& \\ && \ ddots & \\ &&& \ چپ ({\ frac {1} {\ lambda _ {1}}} J_ {m} \ right) ^ {k} \\\ end {bmatrix}} \ rightarrow {\ start {bmatrix} 1 &&&& \\ & 0 &&& \\ && \ ddots & \\ &&& 0 \\\ end {bmatrix}} \ quad {\ text {as}} \ quad k \ to \ invyy.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cec7d61aee7e07ab39497f6cf782f074c415a7fd)


![{\ displaystyle {\ start {تراز شده} b_ {k} & = \ چپ ({\ frac {\ lambda _ {1}} {| \ lambda _ {1} |}} \ راست) ^ {k} {\ frac {c_ {1}} {| c_ {1} |}} {\ frac {v_ {1} + {\ frac {1} {c_ {1}}} V \ چپ ({\ frac {1} {\ lambda _ {1}}} J \ راست) ^ {k} \ چپ (c_ {2} e_ {2} + \ cdots + c_ {n} e_ {n} \ سمت راست)} {\ چپ \ | v_ {1} + {\ frac {1} {c_ {1}}} V \ چپ ({\ frac {1} {\ lambda _ {1}}} J \ راست) ^ {k} \ چپ (c_ {2} e_ { 2} + \ cdots + c_ {n} e_ {n} \ right) \ right \ |}} \\ [6pt] & = e ^ {i \ phi _ {k}} {\ frac {c_ {1}} {| c_ {1} |}} {\ frac {v_ {1}} {\ | v_ {1} \ |}} + r_ {k} \ end {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/024832f7d5c7731b36d56df90fde0723dd480484)






![A = \ left [{\ start {matrix} 1 & 2 & 3 \\ 1 & 2 & 1 \\ 3 & 2 & 1 \\\ end {matrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/100be72a4de1e00d34c2c6cec2fe30120645a778)
![v_ {1} = \ left [{\ start {matrix} 1 \\\ varphi -1 \\ 1 \\\ end {matrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca2f0ca4cc5603861579ef138d645344d4b64cc4)
![v_ {1} \ تقریبی \ چپ [{\ \ شروع {ماتریس} 1 \\ 0.6180 \\ 1 \\\ پایان {ماتریس}} \ راست]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca7733c385d7bc4430a8ac01b7dd179021d7dcd9)
![b_ {1} \ تقریبی \ چپ [{\ start {matrix} -0.57927 \\ - 0.57348 \\ - 0.57927 \\\ end {matrix}} \ right] ، ~ \ mu _ {1} \ تقریبی 5.3355](https://wikimedia.org/api/rest_v1/media/math/render/svg/609ad6cfaa3365a2ae1800753d127496295559d2)
![b_ {2} \ تقریبی \ چپ [{\ \ شروع {matrix} 0.64676 \\ 0.40422 \\ 0.64676 \\\ پایان {matrix}} \ سمت راست] ، right \ mu _ {2} \ تقریبا 5.2418](https://wikimedia.org/api/rest_v1/media/math/render/svg/42a54a4af490f5ee35dee64c401f7f0a774e7da8)
![b_ {3} \ تقریبی \ چپ [{\ start {matrix} -0.64793 \\ - 0.40045 \\ - 0.64793 \\\ end {matrix}} \ right] ، ~ \ mu _ {3} \ تقریبی 5.2361](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec6d7cb6acb7ba1c06ae67090cd5fdc3706b859d)















![L (y) = \ frac {1} {w (x)} \ چپ (- \ frac {d} {dx} \ چپ [p (x) \ frac {dy} {dx} \ راست] + q (x ) y \ درست)](https://wikimedia.org/api/rest_v1/media/math/render/svg/371147c6e1ef449ffd33e67888014e4866665d32)

![\ frac {\ langle {y، Ly} \ rangle} {\ langle {y، y} \ rangle} = \ frac {\ int_a ^ توسط (x) \ سمت چپ (- \ frac {d} {dx} \ سمت چپ [ p (x) \ frac {dy} {dx} \ right] + q (x) y (x) \ right) dx} {\ int_a ^ b {w (x) y (x) ^ 2} dx}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc74991eb4219cc9d071797b1c76c086a0f6509)
![{\ displaystyle {\ start {تراز شده} {\ frac {\ langle {y ، Ly} \ رانگل} {\ langle {y ، y} \ rangle}} & = {\ frac {\ چپ \ {\ int _ {a } ^ {b} y (x) \ چپ (- {\ frac {d} {dx}} \ چپ [p (x) y '(x) \ راست] \ راست) dx \ راست \} + \ چپ \ {\ int _ {a} ^ {b} {q (x) y (x) ^ {2}} \، dx \ right \}} {\ int _ {a} ^ {b} {w (x) y (x) ^ {2}} \ ، dx}} \\ & = {\ frac {\ چپ \ {\ چپ.-y (x) \ چپ [p (x) y '(x) \ راست] \ راست | _ {a} ^ {b} \ right \} + \ left \ {\ int _ {a} ^ {b} y '(x) \ left [p (x) y' (x) \ right] \، dx \ right \} + \ left \ {\ int _ {a} ^ {b} {q (x) y (x) ^ {2}} \، dx \ right \}} {\ int _ {a} ^ {b} w (x) y (x) ^ {2} \، dx}} \\ & = {\ frac {\ left \ {\ left.-p (x) y (x) y '(x) \ راست | _ {a} ^ {b} \ راست \} + \ چپ \ {\ int _ {a} ^ {b} \ چپ [p (x) y '(x) ^ {2} + q (x) y (x) ^ {2} \ right] \، dx \ right \}} {\ int _ {a} ^ {b} {w (x) y (x) ^ {2}} \، dx}}. \ end {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c68f876aa4dd809977dfd4ff2ce4a2cc3bcf852)