ریاضیات

در این بخش ، ما نکات و حقایقی را که برای بحث در آینده لازم است ، معرفی می کنیم. مانند قبل  یک  ماتریس واقعی را با نشان می دهد 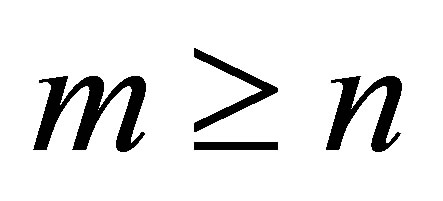. اجازه دهید

(2.1)

یک SVD از ، که در آن  یک IS 

ماتریس متعامد ، 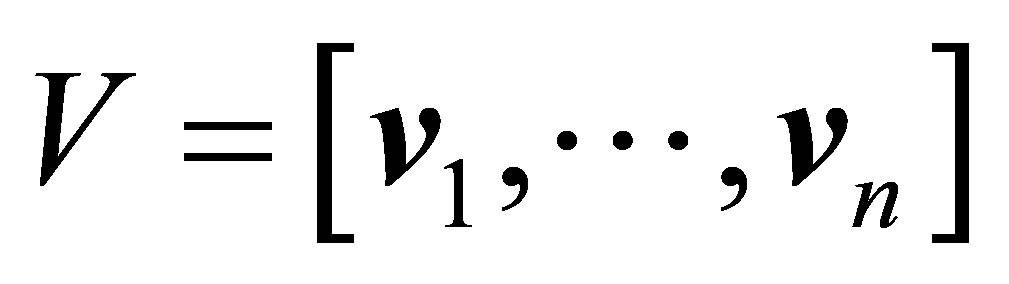یک  ماتریس متعامد است ، و 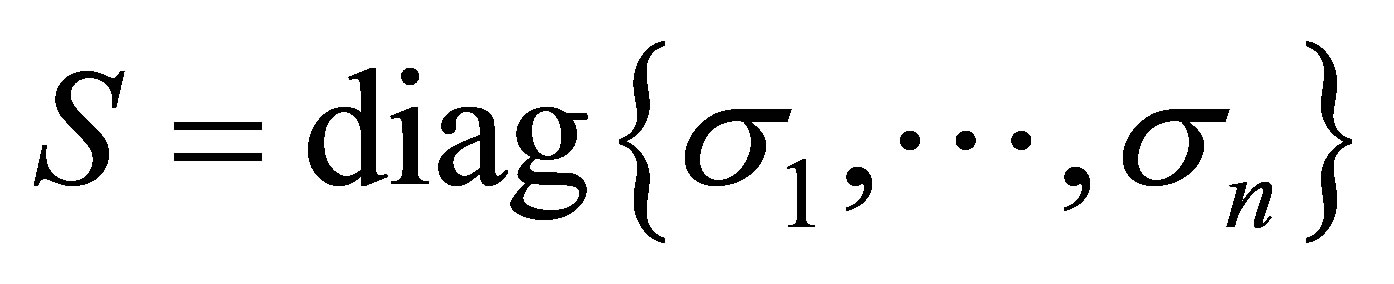 یک  ماتریس مورب است. مقادیر منحصر به فرد  فرض می شود که منفی نبوده و برای ارضای آن مرتب شده باشد

(2.2)

ستون از  و  به نام به سمت چپ بردار منحصر به فرد و بردار منحصر به فرد راست، به ترتیب. این بردارها با معادلات مرتبط هستند

(2.3)

نتیجه بعدی (2.1) برابری است

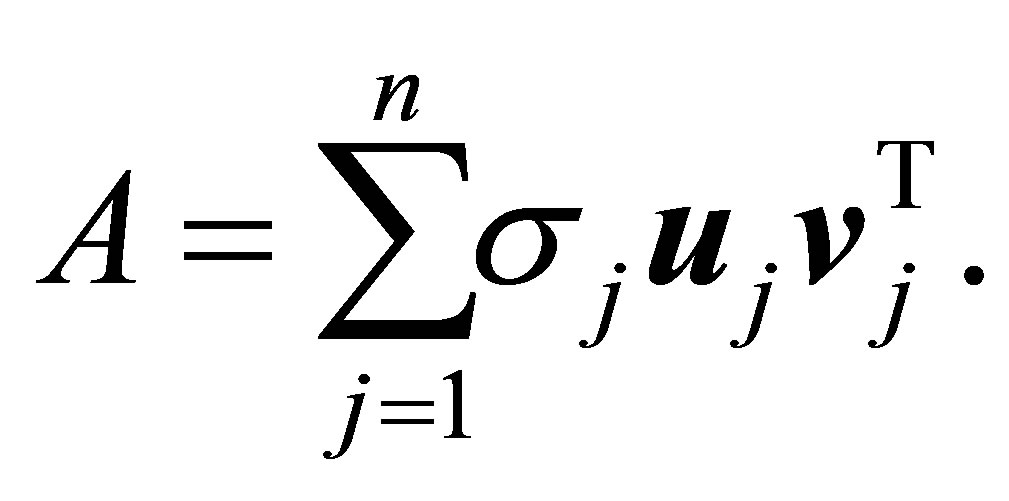(2.4)

علاوه بر این ، اجازه دهید  نشان می دهد رتبه از . سپس ، به وضوح ،

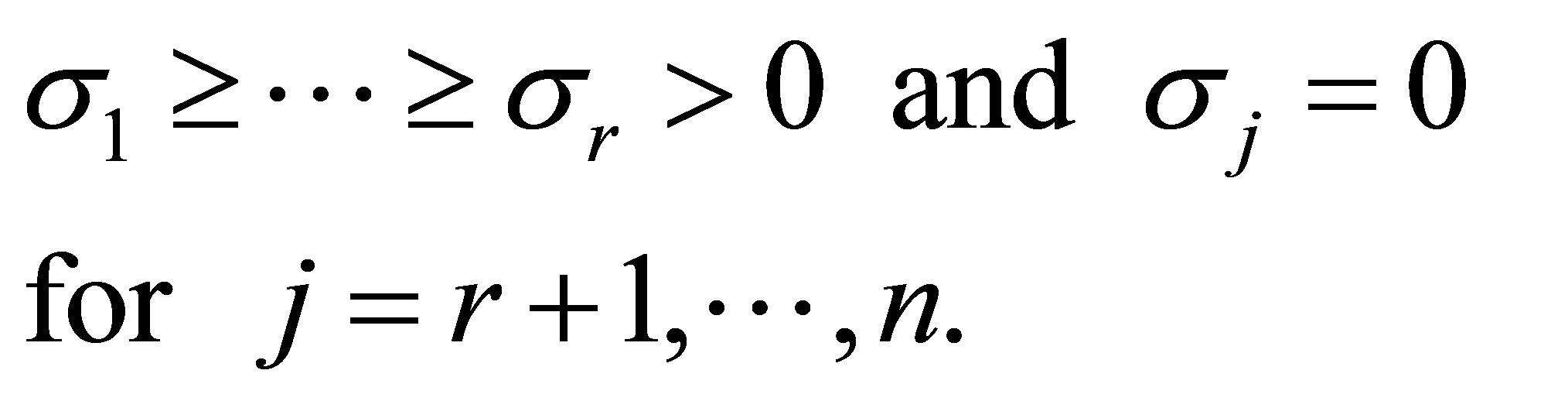(2.5)

بنابراین (2.4) را می توان دوباره نوشت

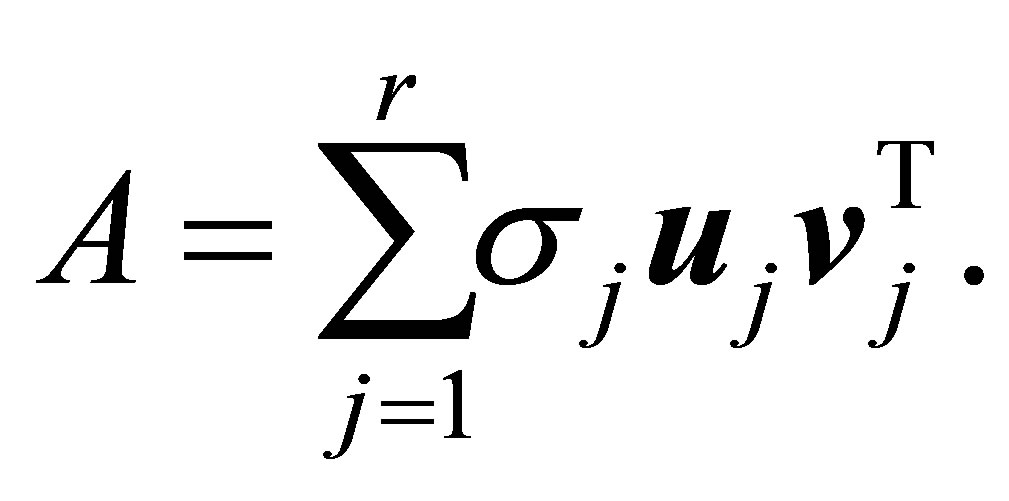(2.6)

اجازه دهید ماتریس ها

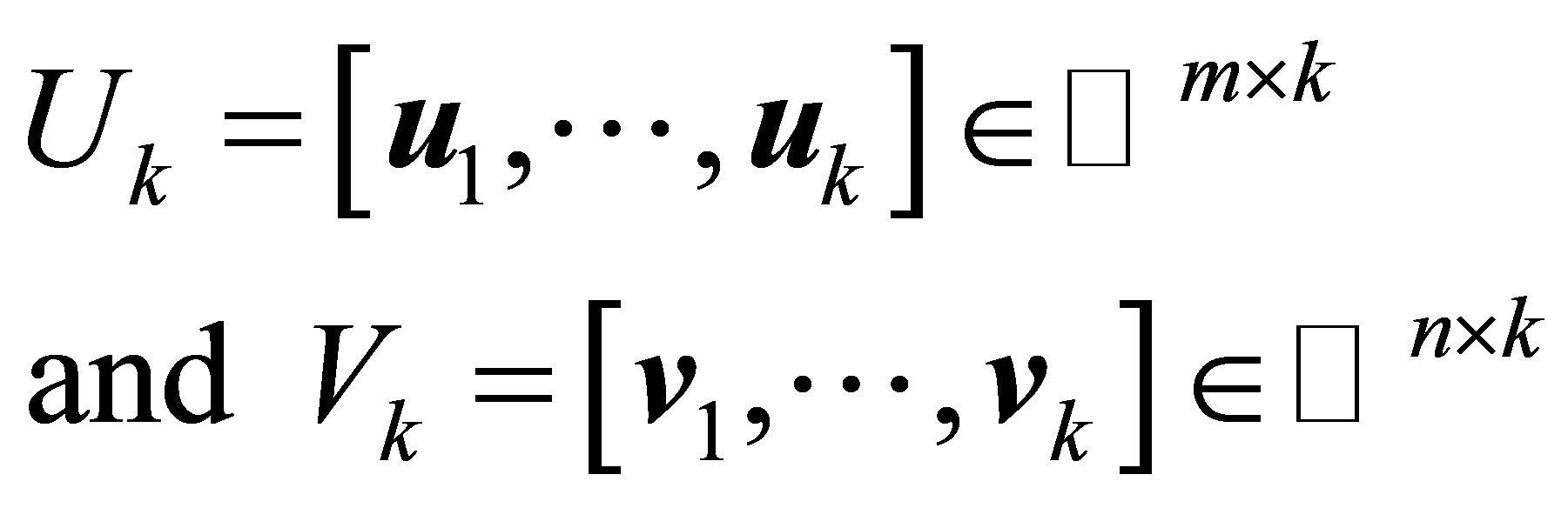(2.7)

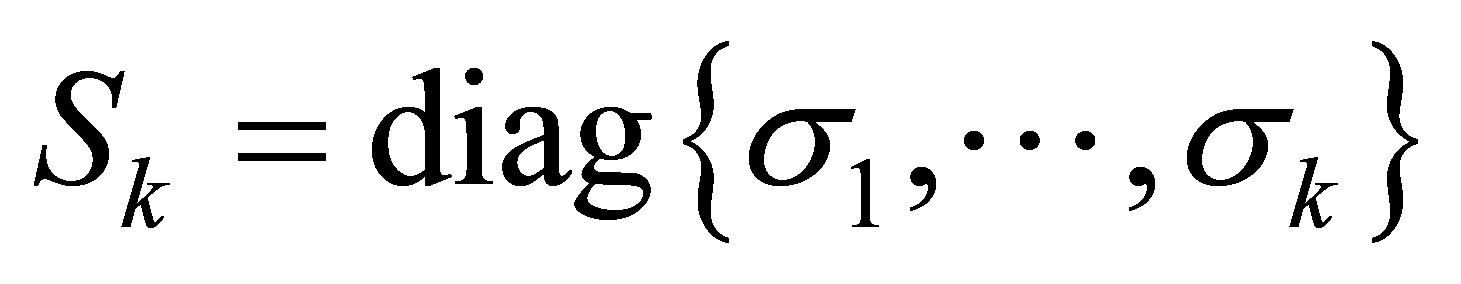به ترتیب از اولین  ستون های U ساخته شده است. اجازه دهید  یک  ماتریس مورب باشد. سپس ماتریس

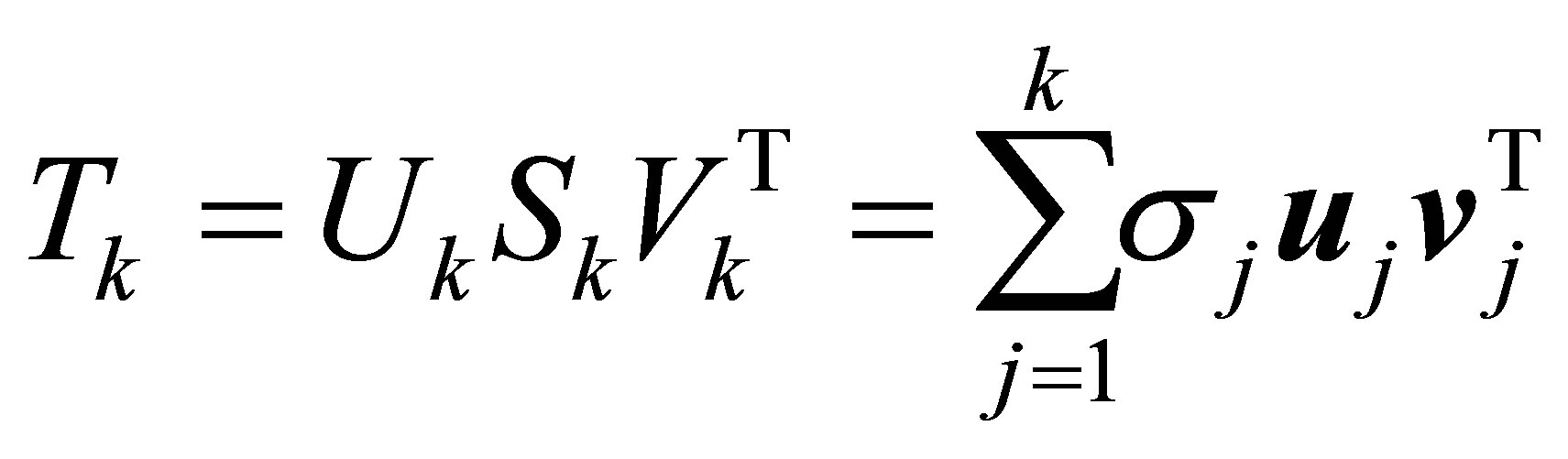(2.8)

 مرتبه- SVD کوتاه شده از نامیده می شود .

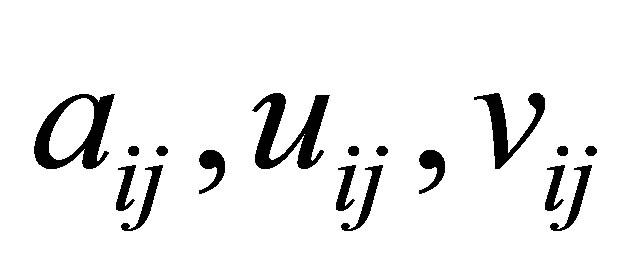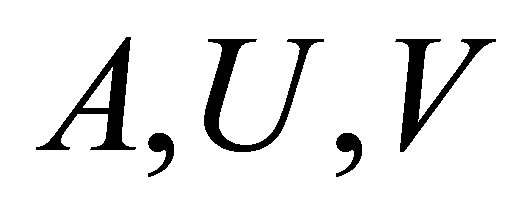اجازه دهید ، به ترتیب  ورودی های ماتریس را مشخص کنید. سپس (2.4) نشان می دهد که

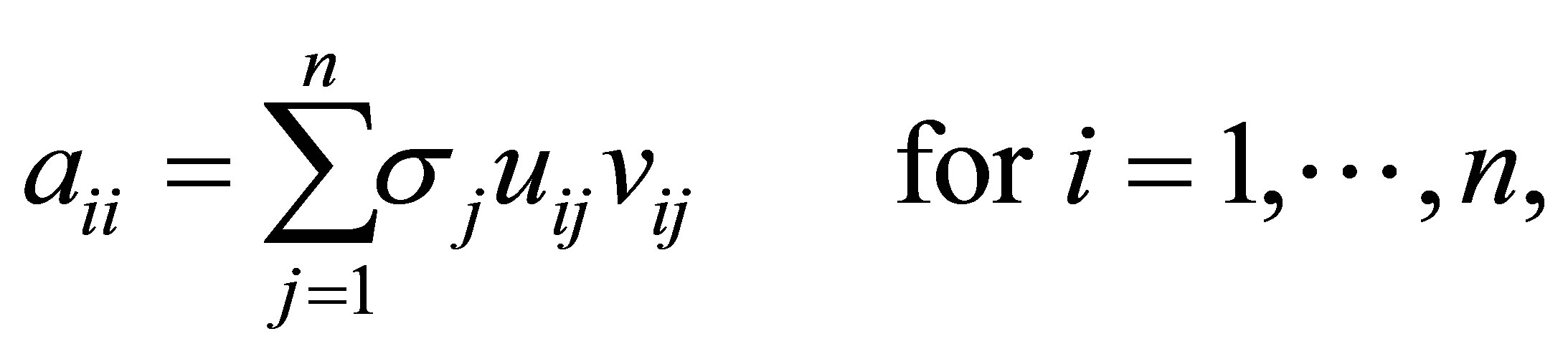(2.9)

و

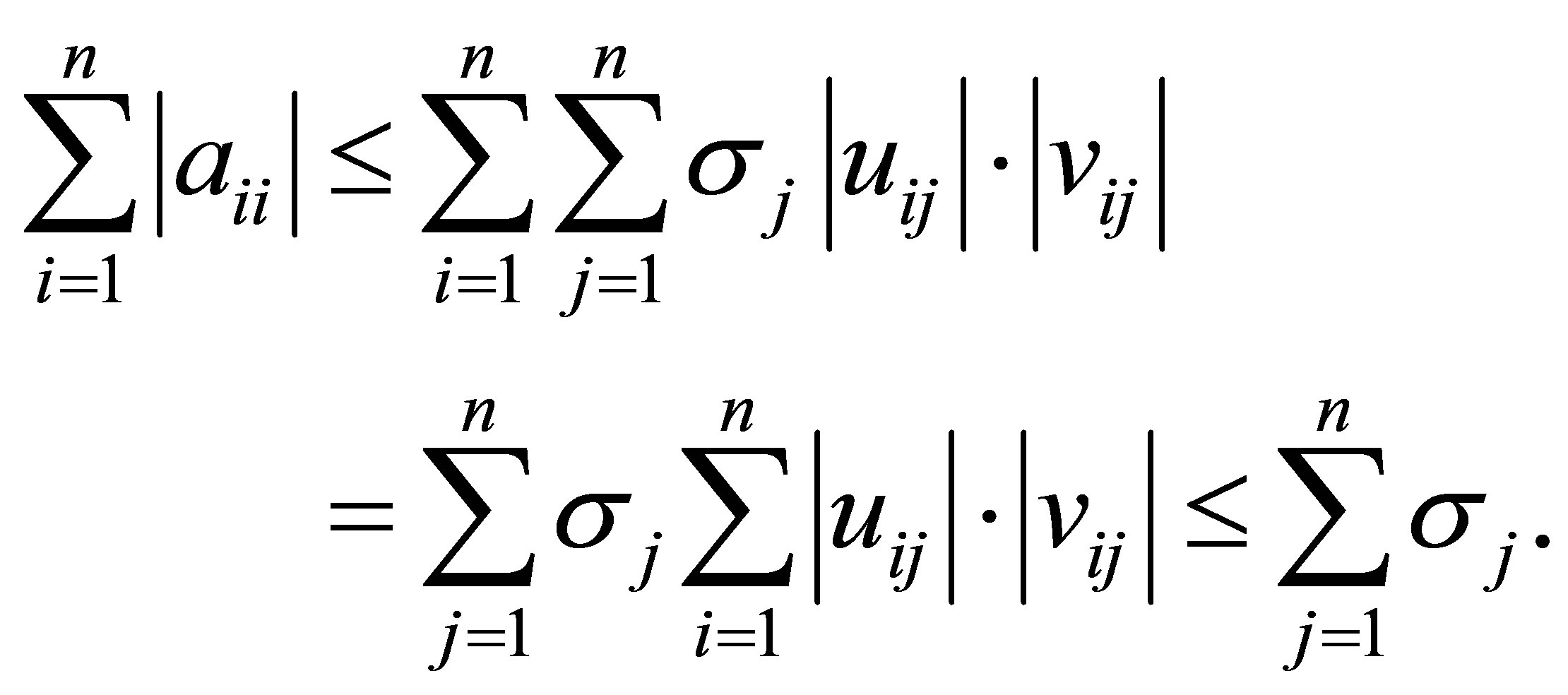(2.10)

که در آن آخرین نابرابری زیر از نابرابری CauchySchwarz و این واقعیت است که ستون از  و  باید طول واحد.

یکی دیگر از ویژگیهای مفید مفاهیم بزرگنمایی و هنجارهای یکپارچه بی ثبات است. به یاد بیاورید که در صورت برابر بودن یک هنجار ماتریس  به  صورت واحد تغییر نمی کند

(2.11)

برای هر ماتریس 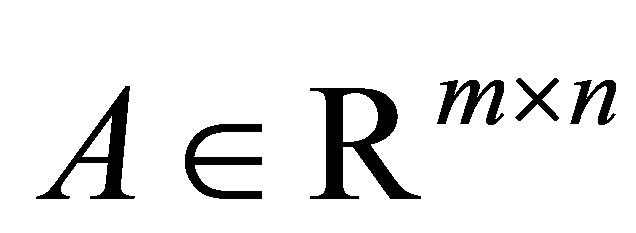و هر جفت ماتریس واحد راضی هستند  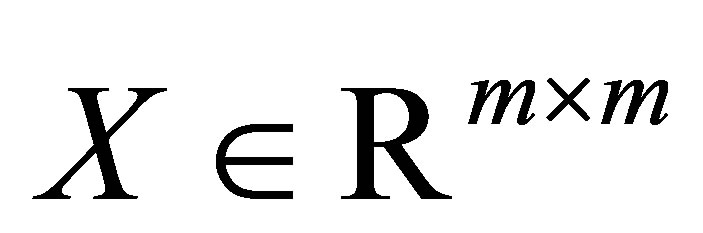و 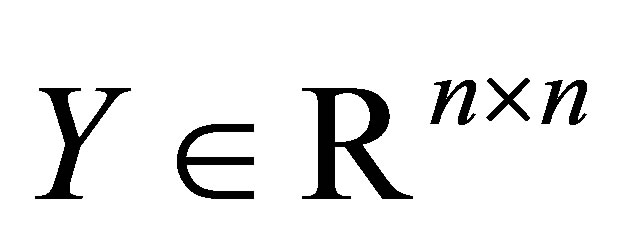. اجازه دهید  و  یک جفت  ماتریس داده شده با مقادیر منفرد باشد

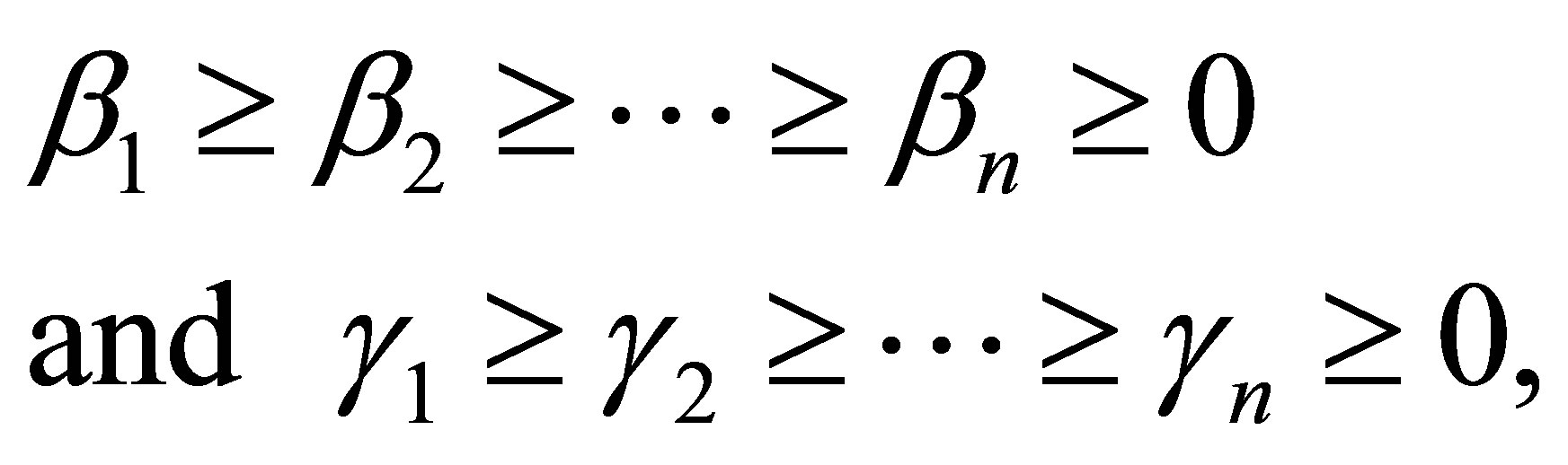
به ترتیب. اجازه دهید 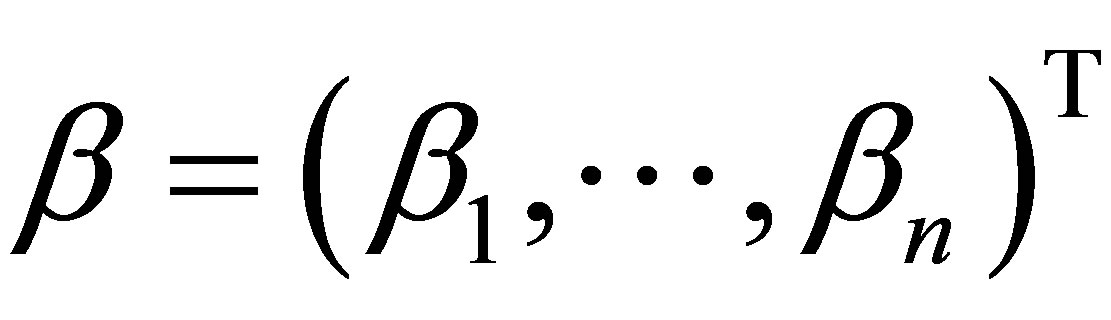 و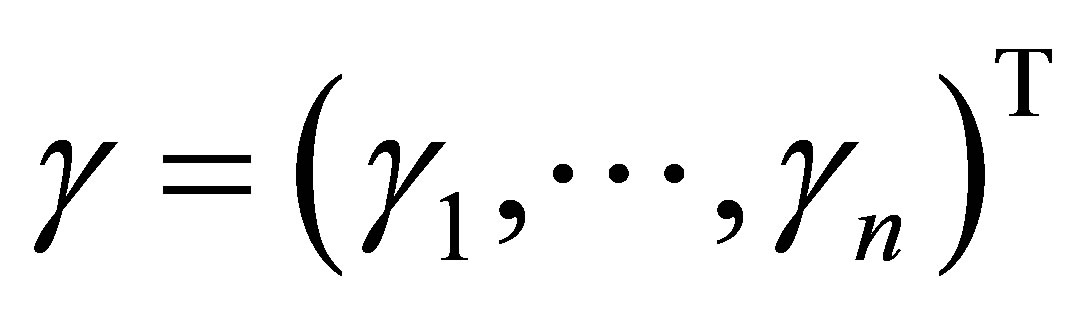 

معنی مربوطه -vectors از ارزش منحصر به فرد. سپس رابطه بزرگ نمایی ضعیف 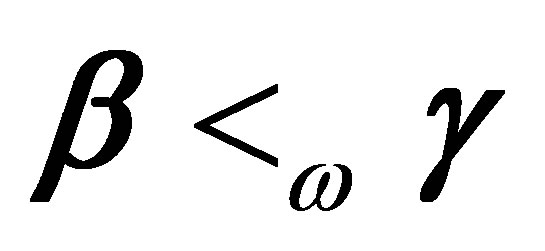 به این معنی است که این بردارها نابرابری ها را برآورده می کنند

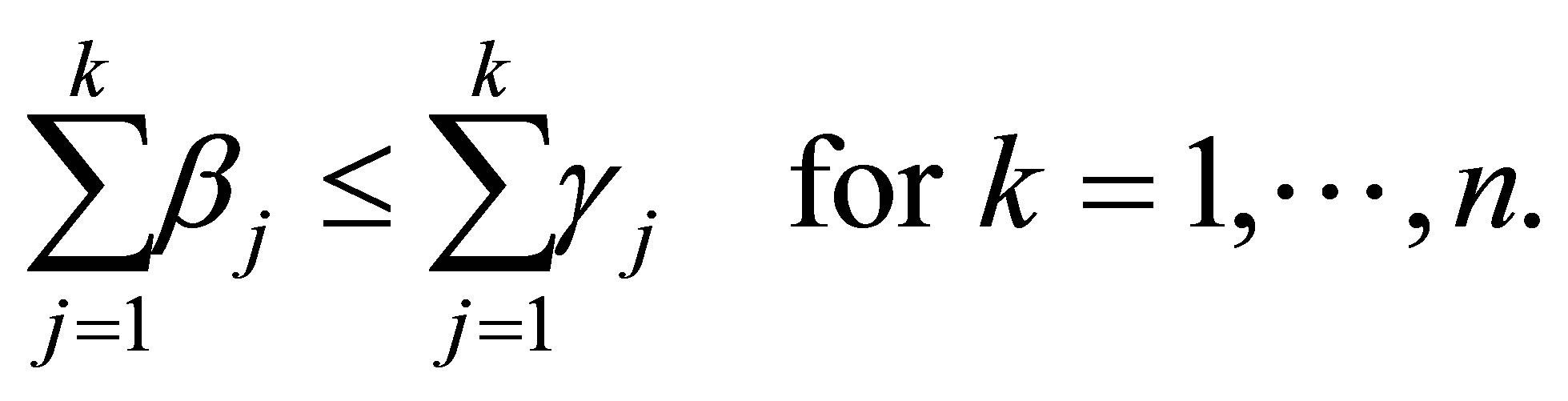(2.12)

در این حالت می گوییم که  توسط ضعیف بزرگ شده یا مقادیر منفرد B به طور ضعیفی توسط آن بزرگ شده است . قضیه تسلط Ky Fan [ 11 ] این دو مفهوم را با هم مرتبط می کند. این مقاله می گوید اگر مقادیر منفرد  توسط آن  نابرابری بزرگ شود

(2.13)

برای هر هنجار واحدی ثابت است. برای اثبات دقیق این واقعیت ، به عنوان مثال ، [1،11،17،22] را ببینید. مشهورترین مثال از یک هنجار منحصر به فرد ، شاید هنجار ماتریس Frobenius است

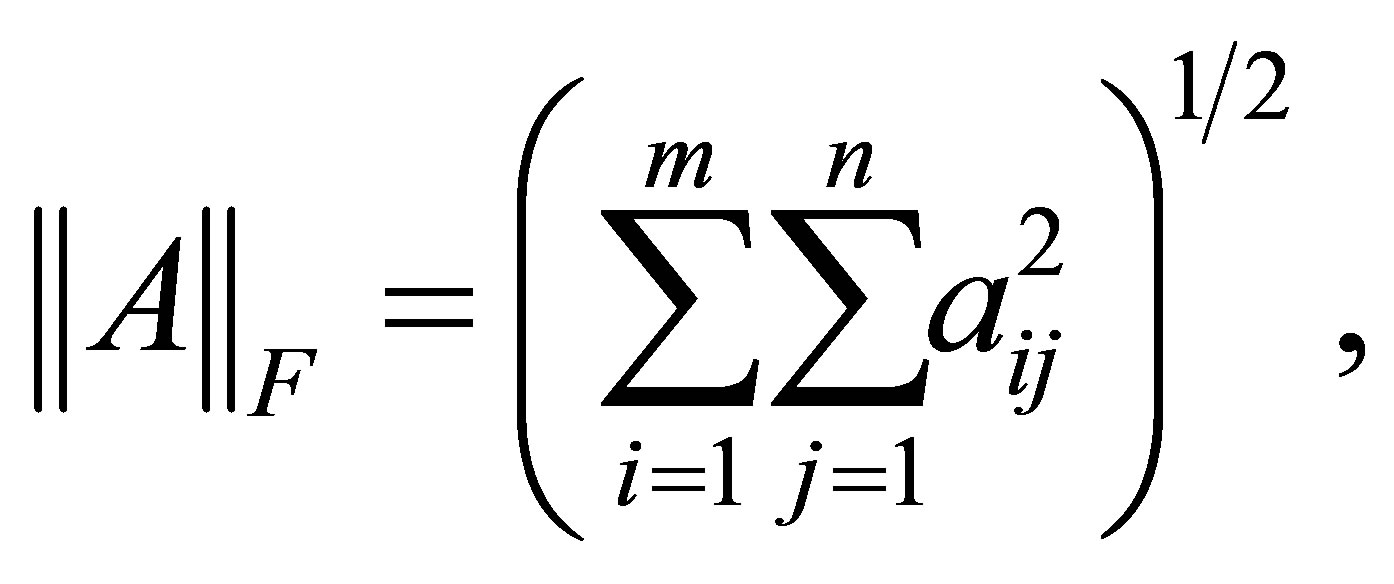(2.14)

که راضی می کند

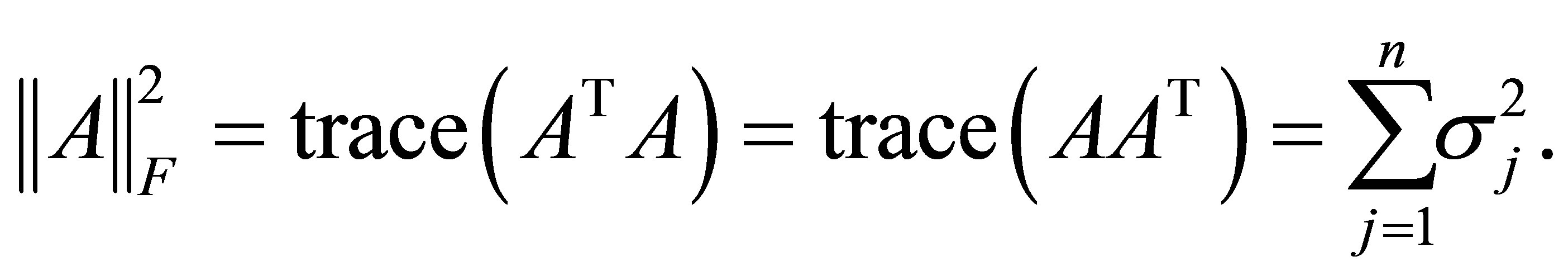(2.15)

مثالهای دیگر Schatten -norms است ،

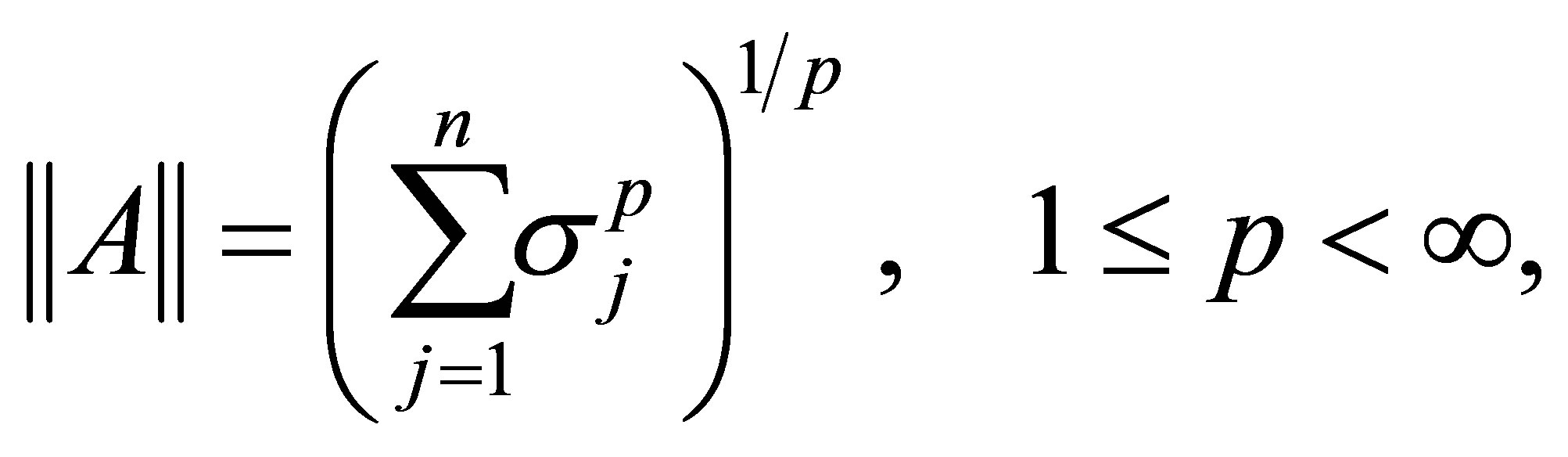(2.16)

و Ky Fan -norms ،

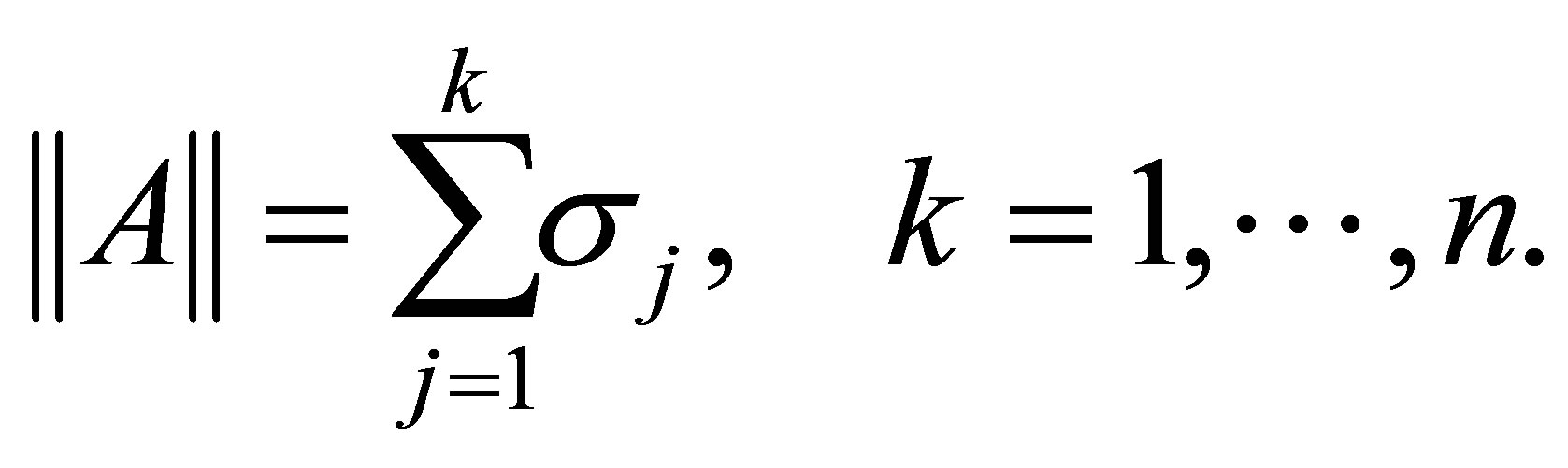(2.17)

هنجار کمیاب ،

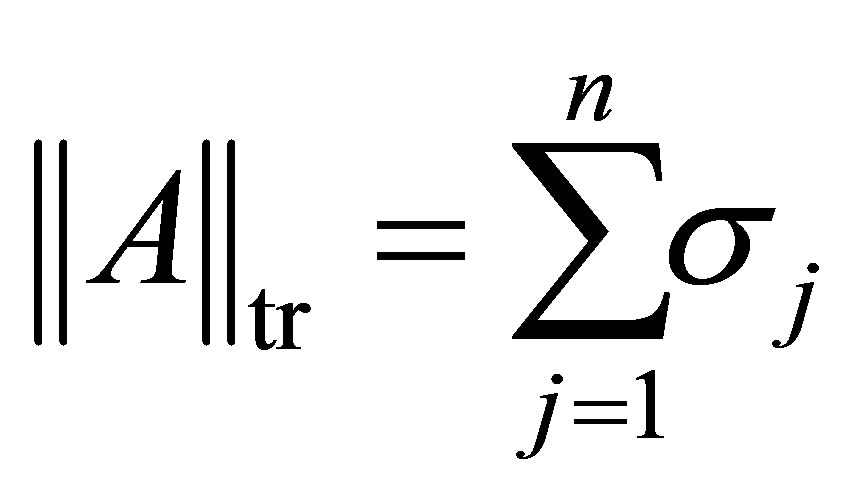(2.18)

برای  و در حالی که هنجار طیفی (2 هنجار) بدست می آید

(2.19)

مطابقت دارد  و .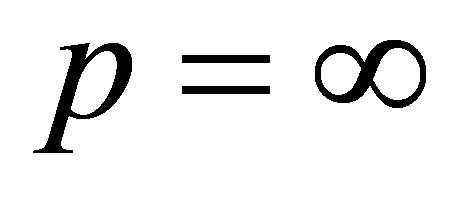

در آخر ، اجازه دهید  و  یک جفت عدد صحیح مثبت داشته باشید ، به گونه ای که

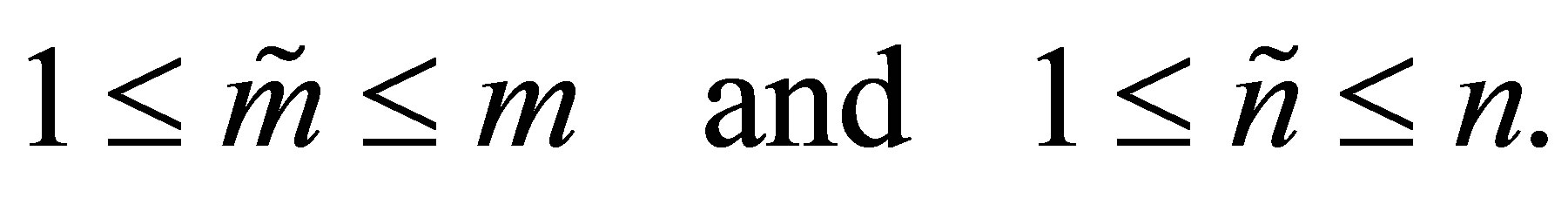
سپس

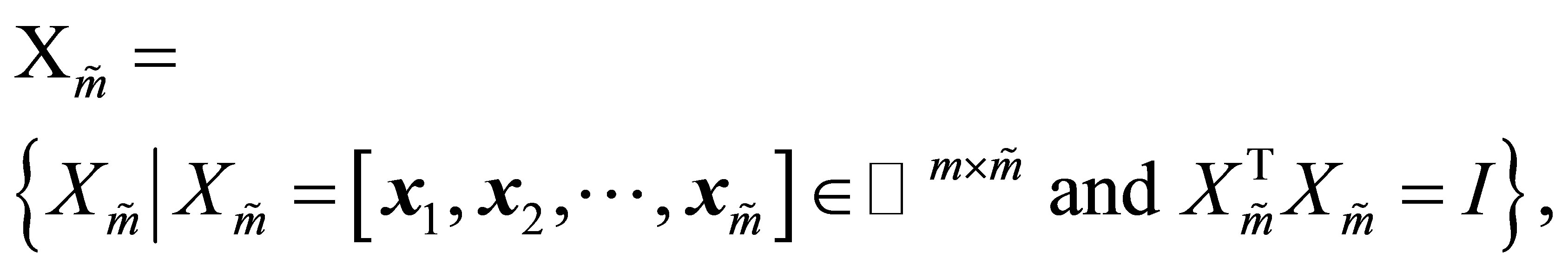(2.20)

و

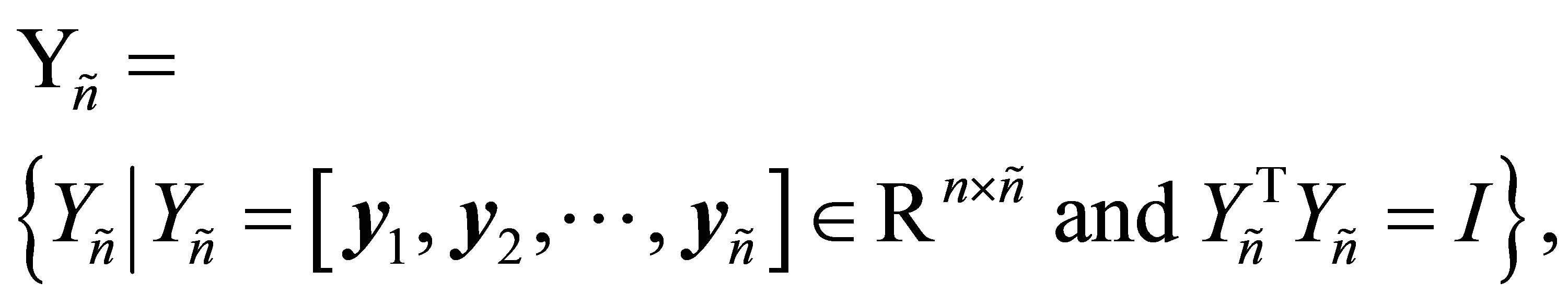(2.21)

منیفولدهای مربوط به استیفل را نشان می دهد. یعنی مجموعه ای از تمام  ماتریس های واقعی با ستون های متعادل ، در حالی  که مجموعه تمام  ماتریس های واقعی با ستون های متعادل است.

منبع

https://file.scirp.org/Html/2-5300515_41122.htm