ریاضیات

8. به حداکثر رساندن (به حداقل رساندن) هنجارهای ماتریس فاکتورهای متعامد

بیایید برگردیم تا ماتریس های ضریب متعامد فرم را در نظر بگیریم (5.1). تعریف کردن

و اجازه دهید

مقادیر منفرد ماتریس ضرایب متعامد را نشان می دهد . ما باید با بررسی مشکلات شروع کنیم

(8.1)

و

(8.2)

 عدد مثبت مشخص کجاست ، . با این حال نتایج آینده ما را قادر می سازد تا خانواده بزرگتری از توابع هدف را مدیریت کنیم. شاید جالب ترین مشکلات این نوع در هنگام  و . در این موارد عملکرد هدف به کاهش می یابد

(8.3)

و

(8.4)

به ترتیب. به طور خاص ، زمان  و  مسئله (8.1) با مسئله اكارت-یانگ (12/6) همزمان است. حل (8.1) و (8.2) براساس پسوندهای "مستطیلی" قضیه های 20 و 21 است. قضیه اول به دلیل تامپسون است [ 37 ]. ما برای اثبات روشن بودن رابطه نزدیک آن با قضیه کاوسی اینترلاس ، اثبات آن را بیان می کنیم.

قضیه 23 (قضیه بینابینی کوشی مستطیلی) اجازه دهید با حذف سطرها و ستون های  ماتریس  بدست آید . یعنی ، و . تعریف کردن

و اجازه دهید

مقادیر واحد را نشان می دهد . سپس

(8.5)

بعلاوه ، تعداد مقادیر مثبت منفرد  از پایین به زیر محدود می شود

که در آن . در نتیجه ، و اگر  اولین  مقادیر مفرد  مرزهای پایین را برآورده می کند

(8.6)

اثبات اثبات این است که  تعداد کلی ردیف ها و ستون های حذف شده از طریق القای روشن است. زیرا  دو مورد وجود دارد که باید در نظر گرفته شود. ابتدا فرض کنید که  با حذف یک ردیف به دست می آید . سپس با استفاده از قضیه 20 با  و  به نتایج مورد نظر می دهد. احتمال دوم این است که  با حذف یک ستون از بدست می آید . در این حالت از قضیه 20 با  و استفاده می شود . استدلالهای مشابه ما را قادر می سازد تا مرحله استقرا را به پایان برسانیم.                               

مشاهده کنید که مرزها (8.5) و (8.6) "سخت" هستند به این معنا که این مرزها می توانند به عنوان برابری برآورده شوند. به عنوان مثال ، یک ماتریس مورب را در نظر بگیرید.

نتیجه گیری 24 (قضیه تفکیک مستطیلی Poincaré) ماتریس را در نظر بگیرید ، کجا  و کجا . اجازه دهید

مقادیر منفرد ، کجا را نشان می دهد . سپس

(8.7)

بعلاوه ، مشخص کنید  که r = رتبه (A) ، و . سپس  و اگر  اولین  مقادیر منفرد  مرزهای پایین را برآورده می کند

(8.8)

اثبات اجازه دهید ماتریس  با تکمیل ستونها بدست آید  تا مبنایی متعادل باشد . اجازه دهید ماتریس  با تکمیل ستونها بدست آید  تا مبنایی متعادل باشد . سپس  ماتریس  همان مقادیر واحد را دارد ، و  از  حذف آخرین  سطرها و  ستون های آخر بدست می آید .

نتیجه گیری 25 با استفاده از نمادهای قبلی ،        

(8.9)

و

(8.10)

بعلاوه ، اگر  آن وقت باشد

(8.11)

و

(8.12)

نابرابری های مشابه وقتی که تابع توان  با هر تابع با ارزش واقعی دیگری که در فاصله زمانی افزایش می یابد جایگزین می شود .

قضیه 26 (یک اصل حداکثر مستطیلی) اجازه دهید  ماتریس  از اولین  ستونها ساخته شود ، و اجازه دهید  ماتریس  از  ستونهای اول ساخته شود . (آن را به یاد بیاورید  و  SVD را تشکیل دهید، به (2.1) - (2.8) مراجعه کنید.) سپس این جفت ماتریس با ارائه مقدار بهینه

. به این معنا که،

(8.13)

با این حال ، ماتریس های راه حل لزوماً منحصر به فرد نیستند.

اثبات اثبات نتیجه مستقیم (8.10) و این واقعیت است که  یک  ماتریس مورب است که ورودی های مورب آن است .              

نتیجه گیری 27 (حداکثر اصل Ky Fan مستطیلی) حالت خاص را در نظر بگیرید که چه زمانی . در این مورد

(8.14)

و مقدار بهینه برای ماتریسها بدست می آید  و .

نتیجه گیری 28 مورد خاص را در نظر بگیرید وقتی که . در این مورد

(8.15)

و مقدار بهینه برای ماتریسها بدست می آید  و . بعلاوه ، اگر  پس از آن (8.15) به (12/6) کاهش یابد. این یک روش جایگزین برای اثبات قضیه اكارت-یانگ است.

قضیه 29 (یک اصل حداقل مستطیلی) اجازه دهید با حذف ستون های اول  ماتریس  بدست آید . اجازه دهید با حذف ماتریس حاصل شود

ستون به روش زیر: اگر  پس از آن  از اول تشکیل  ستون از . در غیر این صورت، هنگامی که ، اولین  ستون از  اولین هستند  ستون از ، و ستون بقیه  آخرین می  ستون از. سپس ماتریس  و  حل مشکل حداقل (8.2). مقدار بهینه (8.2) به عدد صحیح بستگی دارد . اگر  مقدار بهینه برابر با صفر باشد. در غیر این صورت ، چه زمانی

، مقدار بهینه برابر است .

اثبات اجازه دهید با حذف اولین ستون های  ماتریس  از  ماتریس هویت بدست آید . سپس، به وضوح، . به طور مشابه، تعریف می شود ماتریس به طوری که . به این معنا که،  با حذف ستونهای مربوطه از ماتریس هویت بدست می آید . با در دست داشتن این نشانه ها (2.1) دلالت بر برابری ها دارد

بنابراین ماتریس  از  طریق حذف  سطرها و  ستون های مربوطه بدست می آید .

مشاهده کنید که ورودی های غیر صفر باقیمانده  مقادیر منفرد این ماتریس هستند. همچنین توجه داشته باشید که قانون حذف سطرها و ستون ها از  هدف این است که اندازه ورودی های غیر صفر باقیمانده را تا حد ممکن کوچک کند: محصول  اولین  ردیف های بزرگترین  مقادیر منفرد را حذف می کند. سپس محصول  بزرگترین مقادیر بعدی بعدی را نابود می کند . ورودی های غیر صفر باقی مانده از  این رو کمترین ورودی هایی هستند که می توانیم بدست آوریم.  به طور واضح ، تعداد مقادیر مثبت منفرد در ، است . بهینه بودن راه حل ما از (8.8) و (12.12) ناشی می شود.                           

یکی دیگر از جفت ماتریس است که حل (8.2) است با معکوس کردن ترتیب که در آن ما سطر و ستون از حذف به دست آورد شروع با حذف اولین:  ستون از ، که شامل  بزرگترین مقادیر منفرد. سپس  ردیف های بزرگترین مقادیر  بعدی را حذف کنید .

نتیجه گیری 30 (حداقل اصل مستطیلی Ky Fan) مورد خاص را در نظر بگیرید که چه زمانی  و . در این مورد

(8.16)

و مقدار بهینه برای ماتریسها بدست می آید  و .

نتیجه گیری 31 مورد خاص را در نظر بگیرید وقتی  و . در این مورد

(8.17)

و مقدار بهینه برای ماتریسها بدست می آید  و .

قضیه بعدی نتایج ما را به هنجارهای خودسرانه تغییرناپذیر گسترش می دهد.

قضیه 32 اجازه دهید  یک هنجار منحصر به فرد ثابت باشد . سپس ماتریس ها  و ، که (8.1) را حل می کنند ، مسئله را نیز حل می کنند

(8.18)

به همین ترتیب ماتریس ها  و (8.2) را حل می کنند ، همچنین مسئله را حل می کنند

(8.19)

اثبات از (8.7) می بینیم که مقادیر منفرد توسط مقادیر اصلی بزرگ می 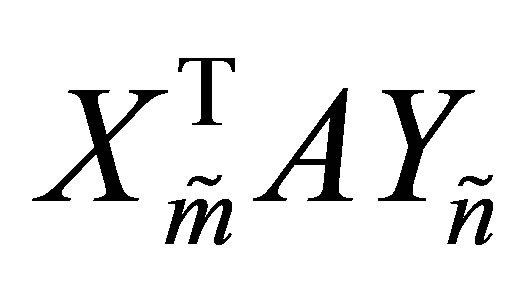 شوند . این نشان می دهد که

(8.20)

که ادعای اول را ثابت می کند. به طور مشابه ، (8.8) به این معنی است که مقادیر منفرد توسط مقادیر مربوط  به بزرگ می شوند . این نشان می دهد که

(8.21)

که ادعای دوم را اثبات می کند.                  

منبع

https://file.scirp.org/Html/2-5300515_41122.htm