توسط علی رضا نقش نیلچی
| چهارشنبه هفتم تیر ۱۴۰۲ | 2:34
مختصات چرخه ای و لحظه ای حفظ شده [ ویرایش ]
یکی از ویژگی های مهم لاگرانژ این است که مقادیر حفظ شده را می توان به راحتی از آن خواند. تکانه تعمیم یافته "به طور متعارف مزدوج به" مختصات q i با تعریف می شود

اگر L لاگرانژی به مختصاتی q i وابسته نباشد ، بلافاصله از معادلات اویلر-لاگرانژ نتیجه میشود که

و یکپارچه سازی نشان می دهد که تکانه تعمیم یافته متناظر برابر با یک مقدار ثابت و یک کمیت حفظ شده است. این یک مورد خاص از قضیه نوتر است . چنین مختصاتی را "حلقه ای" یا "غیر قابل توجه" می نامند.
برای مثال، یک سیستم ممکن است لاگرانژی داشته باشد

جایی که r و z طول هایی در امتداد خطوط مستقیم هستند، s طول قوس در امتداد برخی از منحنی ها، و θ و φ زاویه هستند. توجه کنید z ، s و φ همگی در لاگرانژ وجود ندارند، حتی اگر سرعت آنها نباشد. سپس لحظه لحظه

همه کمیت های حفظ شده هستند. واحدها و ماهیت هر تکانه تعمیم یافته به مختصات مربوطه بستگی دارد. در این مورد p z یک تکانه انتقالی در جهت z است، ps نیز یک تکانه انتقالی در امتداد منحنی s اندازه گیری می شود، و p φ یک تکانه زاویه ای در صفحه است که زاویه φ در آن اندازه گیری می شود. هر چند حرکت پیچیده باشد سیستم این است که همه مختصات و سرعت ها به گونه ای تغییر می کنند که این لحظه ها حفظ شوند.
انرژی [ ویرایش ]
تعریف [ ویرایش ]
با توجه به لاگرانژی، انرژی سیستم مکانیکی مربوطه، طبق تعریف ،
انرژی سیستم مکانیکی مربوطه، طبق تعریف ،

تغییر ناپذیری تحت تبدیل مختصات [ ویرایش ]
در هر لحظه انرژی تحت تغییرات مختصات فضای پیکربندی ثابت است
انرژی تحت تغییرات مختصات فضای پیکربندی ثابت است ، یعنی
، یعنی

علاوه بر این نتیجه، اثبات زیر نشان میدهد که تحت چنین تغییر مختصات، مشتقات به عنوان ضرایب یک فرم خطی تغییر می کند.
به عنوان ضرایب یک فرم خطی تغییر می کند.
نشان می دهداثبات
حفاظت [ ویرایش ]
در مکانیک لاگرانژی، سیستم بسته است اگر و فقط اگر لاگرانژی باشد به صراحت به زمان بستگی ندارد. قانون بقای انرژی بیان می کند که انرژی
به صراحت به زمان بستگی ندارد. قانون بقای انرژی بیان می کند که انرژی یک سیستم بسته یک انتگرال حرکت است .
یک سیستم بسته یک انتگرال حرکت است .
به طور دقیق تر، اجازه دهید افراطی بودن . (به عبارت دیگر،
افراطی بودن . (به عبارت دیگر، معادلات اویلر-لاگرانژ را برآورده می کند). در نظر گرفتن کل مشتق زمانی از
معادلات اویلر-لاگرانژ را برآورده می کند). در نظر گرفتن کل مشتق زمانی از در امتداد این اکسترمال و استفاده از معادلات EL منجر به
در امتداد این اکسترمال و استفاده از معادلات EL منجر به
![{\displaystyle -{\frac {\partial L}{\partial t}}{\biggl |}_{\mathbf {q} (t)}={\frac {\mathrm {d} }{\mathrm {d } t}}\left[E{\biggl |}_{\mathbf {q} (t)}\راست].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8bb04875cb2c57a1ce578378edae29d1f1797)
اگر لاگرانژی پس صراحتاً به زمان بستگی ندارد،
پس صراحتاً به زمان بستگی ندارد، بنابراین
بنابراین در واقع یک انتگرال حرکت است، به این معنی که
در واقع یک انتگرال حرکت است، به این معنی که

از این رو، انرژی حفظ می شود.
انرژی های جنبشی و بالقوه [ ویرایش ]
همچنین نتیجه می شود که انرژی جنبشی تابع همگن درجه 2 در سرعت های تعمیم یافته است. علاوه بر این، اگر پتانسیل V فقط تابع مختصات و مستقل از سرعت باشد، با محاسبه مستقیم یا استفاده از قضیه اویلر برای توابع همگن ، نتیجه میشود که

تحت همه این شرایط، [33] ثابت

انرژی کل سیستم است. انرژی های جنبشی و پتانسیل همچنان با تکامل سیستم تغییر می کنند، اما حرکت سیستم به گونه ای خواهد بود که مجموع آنها، انرژی کل، ثابت باشد. این یک ساده سازی ارزشمند است، زیرا انرژی E یک ثابت ادغام است که به عنوان یک ثابت دلخواه برای مسئله به حساب می آید، و ممکن است بتوان سرعت های این رابطه انرژی را برای حل مختصات ادغام کرد. در صورتی که سرعت یا انرژی جنبشی یا هر دو به زمان بستگی داشته باشد، انرژی حفظ نمی شود .
شباهت مکانیکی [ ویرایش ]
نوشتار اصلی: شباهت مکانیکی
اگر انرژی پتانسیل تابعی همگن از مختصات و مستقل از زمان باشد، [34] و همه بردارهای موقعیت با همان ثابت غیرصفر α ، r k ′ = α r k مقیاس بندی می شوند ، به طوری که

و زمان با ضریب β , t = βt , سپس سرعتهای v k با ضریب α / β و انرژی جنبشی T با ( α / β ) 2 مقیاس می شوند . کل لاگرانژی با همان فاکتور اگر مقیاس شده است

از آنجایی که طول ها و زمان ها مقیاس بندی شده اند، مسیر ذرات در سیستم مسیرهای هندسی مشابهی را دنبال می کنند که در اندازه متفاوت هستند. طول l پیموده شده در زمان t در مسیر اصلی مطابق با طول جدید l' پیموده شده در زمان t' در مسیر جدید است که توسط نسبت ها داده می شود.

ذرات متقابل [ ویرایش ]
برای یک سیستم معین، اگر دو زیرسیستم A و B غیر متقابل باشند، L لاگرانژی سیستم کلی مجموع لاگرانژی L A و L B برای زیرسیستمها است: [29]

اگر آنها تعامل داشته باشند این امکان پذیر نیست. در برخی موقعیتها، ممکن است بتوان لاگرانژی سیستم L را به مجموع لاگرانژیهای غیر متقابل، به اضافه L AB لاگرانژی دیگری که حاوی اطلاعاتی درباره برهمکنش است، جدا کرد.

این ممکن است از نظر فیزیکی با در نظر گرفتن لاگرانژهای غیر متقابل به عنوان انرژی جنبشی ایجاد شود، در حالی که لاگرانژین برهمکنش کل انرژی پتانسیل سیستم است. همچنین، در حالت محدود کننده تعامل ناچیز، L AB به سمت صفر کاهش مییابد تا حالت غیر متقابل بالا کاهش یابد.
گسترش بیش از دو زیرسیستم غیر متقابل ساده است - لاگرانژی کلی مجموع لاگرانژهای جداگانه برای هر زیرسیستم است. اگر فعل و انفعالاتی وجود داشته باشد، لاگرانژی های تعاملی ممکن است اضافه شوند.
مثالها [ ویرایش ]
مثالهای زیر معادلات لاگرانژ از نوع دوم را برای مسائل مکانیکی اعمال میکنند.
نیروی محافظه کار [ ویرایش ]
ذره ای به جرم m تحت تأثیر نیروی محافظه کارانه ناشی از گرادیان ∇ پتانسیل اسکالر حرکت می کند .

اگر تعداد ذرات بیشتر باشد، مطابق با نتایج فوق، انرژی جنبشی کل مجموع تمام انرژیهای جنبشی ذرات است و پتانسیل تابعی از همه مختصات است.
مختصات دکارتی [ ویرایش ]
لاگرانژی ذره را می توان نوشت

معادلات حرکت برای ذره با استفاده از معادله اویلر-لاگرانژ ، برای مختصات x پیدا می شود.

با مشتقات

از این رو

و به طور مشابه برای مختصات y و z . با جمع آوری معادلات به صورت برداری پیدا می کنیم

که قانون دوم حرکت نیوتن برای ذره ای است که تحت یک نیروی محافظه کار است.
مختصات قطبی در دو بعدی و سه بعدی [ ویرایش ]
با استفاده از مختصات کروی (r، θ ، φ ) که معمولاً در فیزیک استفاده می شود (قرارداد ISO 80000-2:2019)، که در آن r فاصله شعاعی تا مبدأ است، θ زاویه قطبی است (همچنین به عنوان همپوشانی، زاویه اوج، زاویه معمولی نیز شناخته می شود. ، یا زاویه شیب)، و φ زاویه ازیموتال است، لاگرانژ برای پتانسیل مرکزی است

بنابراین، در مختصات کروی، معادلات اویلر-لاگرانژ هستند



مختصات φ چرخه ای است زیرا در لاگرانژی ظاهر نمی شود، بنابراین تکانه حفظ شده در سیستم، تکانه زاویه ای است.

که در آن r ، θ و dφ/dt همگی می توانند با زمان تغییر کنند، اما فقط به گونه ای که p φ ثابت باشد.
لاگرانژ در مختصات قطبی دوبعدی با تثبیت θ به مقدار ثابت π /2 بازیابی می شود.
آونگ روی تکیه گاه متحرک [ ویرایش ]

طرحی از وضعیت با تعریف مختصات (برای بزرگنمایی کلیک کنید)
آونگی به جرم m و طول ℓ را در نظر بگیرید که به تکیهگاهی با جرم M متصل است که میتواند در امتداد یک خط حرکت کند.ایکس -جهت. اجازه دهیدایکس
-جهت. اجازه دهیدایکس مختصات در امتداد خط تکیه گاه باشد، و اجازه دهید موقعیت آونگ را با زاویه نشان دهیم
مختصات در امتداد خط تکیه گاه باشد، و اجازه دهید موقعیت آونگ را با زاویه نشان دهیم از عمودی مختصات و مولفه های سرعت آونگ باب هستند
از عمودی مختصات و مولفه های سرعت آونگ باب هستند

مختصات تعمیم یافته را می توان در نظر گرفتایکس و
و . انرژی جنبشی سیستم پس از آن است
. انرژی جنبشی سیستم پس از آن است

و انرژی پتانسیل است

دادن لاگرانژ
![{\displaystyle {\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1 {2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right ){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^ {2}{\dot {\theta }}^{2}+mg\ell \cos \theta \,.\end{آرایه}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcea9ca5dd9452880b94f4315f2430d4f9c88684)
از آنجا کهایکس در لاگرانژی وجود ندارد، یک مختصات چرخه ای است. تکانه حفظ شده است
در لاگرانژی وجود ندارد، یک مختصات چرخه ای است. تکانه حفظ شده است

و معادله لاگرانژ برای مختصات پشتیبانیایکس است
است

معادله لاگرانژ برای زاویه است
است
![\frac{\mathrm{d}}{\mathrm{d}t}\left[ m( \dot x \ell \cos\theta + \ell^2 \dot\theta ) \right] + m \ell (\ نقطه x \dot \theta + g) \sin\theta = 0;](https://wikimedia.org/api/rest_v1/media/math/render/svg/27ef95240aa335e09f85c8c7ef67a7301547c588)
و ساده کردن

این معادلات ممکن است کاملاً پیچیده به نظر برسند، اما یافتن آنها با قوانین نیوتن مستلزم شناسایی دقیق همه نیروها بود که بسیار پر زحمت و مستعد خطا بودند. با در نظر گرفتن موارد محدود می توان صحت این سیستم را تأیید کرد: به عنوان مثال،ایکس¨→0 باید معادلات حرکت یک آونگ ساده را که در یک قاب اینرسی ساکن است ، ارائه دهد ، در حالی که¨→0
باید معادلات حرکت یک آونگ ساده را که در یک قاب اینرسی ساکن است ، ارائه دهد ، در حالی که¨→0 باید معادلات یک آونگ در یک سیستم دائماً شتابدهنده و غیره را ارائه دهد. علاوه بر این، با توجه به شرایط شروع مناسب و یک گام زمانی انتخابی، با گام برداشتن از نتایج به صورت تکراری، به دست آوردن نتایج به صورت عددی امری بیاهمیت است .
باید معادلات یک آونگ در یک سیستم دائماً شتابدهنده و غیره را ارائه دهد. علاوه بر این، با توجه به شرایط شروع مناسب و یک گام زمانی انتخابی، با گام برداشتن از نتایج به صورت تکراری، به دست آوردن نتایج به صورت عددی امری بیاهمیت است .
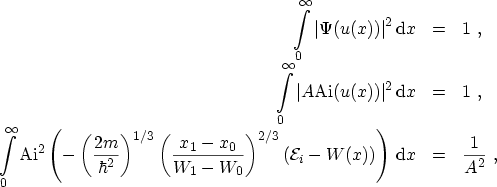
![]() . با
. با ![]() ،
، ![]() و میدان الکتریکی
و میدان الکتریکی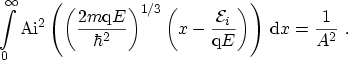
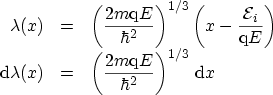
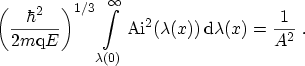
![]()



 بیش از دو برابر مقدار شکاف انرژی ابررسانا Δ است. در دمای محدود، یک جریان تونلی شبه ذره کوچک - به نام جریان زیر شکاف - حتی برای ولتاژهای کمتر از دو برابر شکاف انرژی به دلیل ارتقای حرارتی شبه ذرات بالای شکاف وجود دارد.
بیش از دو برابر مقدار شکاف انرژی ابررسانا Δ است. در دمای محدود، یک جریان تونلی شبه ذره کوچک - به نام جریان زیر شکاف - حتی برای ولتاژهای کمتر از دو برابر شکاف انرژی به دلیل ارتقای حرارتی شبه ذرات بالای شکاف وجود دارد. منحنی جریان-ولتاژ dc هم مراحل و هم مراحل شاپیرو را به دلیل تونل زنی به کمک فوتون نشان می دهد. گام های شاپیرو از پاسخ ابرجریان به وجود می آیند و در ولتاژهای برابر با�ساعت�/(2ه)
منحنی جریان-ولتاژ dc هم مراحل و هم مراحل شاپیرو را به دلیل تونل زنی به کمک فوتون نشان می دهد. گام های شاپیرو از پاسخ ابرجریان به وجود می آیند و در ولتاژهای برابر با�ساعت�/(2ه) ، جایی کهساعت
، جایی کهساعت

 یک
یک  نسبت به ولتاژ شکاف
نسبت به ولتاژ شکاف  O3
O3 ) با ضخامت معمولی چند
) با ضخامت معمولی چند  ). یک سیگنال فرکانس بالا از یک شی نجومی مورد علاقه به همراه یک منبع
). یک سیگنال فرکانس بالا از یک شی نجومی مورد علاقه به همراه یک منبع  جایی که�
جایی که� یک ثابت تعریف شده بین المللی است که اساساً برابر است2ه/ساعت
یک ثابت تعریف شده بین المللی است که اساساً برابر است2ه/ساعت . این مراحل یک تبدیل دقیق از فرکانس به ولتاژ را فراهم می کند. از آنجایی که فرکانس را می توان با دقت بسیار بالایی اندازه گیری کرد، این اثر به عنوان مبنای استاندارد ولتاژ جوزفسون استفاده می شود که تعریف بین المللی ولت "
. این مراحل یک تبدیل دقیق از فرکانس به ولتاژ را فراهم می کند. از آنجایی که فرکانس را می توان با دقت بسیار بالایی اندازه گیری کرد، این اثر به عنوان مبنای استاندارد ولتاژ جوزفسون استفاده می شود که تعریف بین المللی ولت " 







 سپس به دو بخش حقیقی و خیالی تقسیم می شود:
سپس به دو بخش حقیقی و خیالی تقسیم می شود:

 در واحدهای اتمی (au). خطوط یکپارچه نشان دهنده
در واحدهای اتمی (au). خطوط یکپارچه نشان دهنده  .
. برای ارضای بخش واقعی معادله؛ برای یک حد کلاسیک خوب که با بالاترین توان
برای ارضای بخش واقعی معادله؛ برای یک حد کلاسیک خوب که با بالاترین توان 



 و
و
![{\displaystyle \Psi (x)\approx C{\frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(EV(x)\right )}}+\theta }}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(EV(x)\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5ee1989ca3279bca4fb4f1fea48a0c48c724f1e)
 و
و
![{\displaystyle \Psi (x)\approx {\frac {C_{+}e^{+\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x )-E\right)}}}+C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\ راست)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4bff4af65fcfda75cb594e31f867ce95e972d22)
 . دور از تپه بالقوه، ذره شبیه به یک موج آزاد و نوسانی عمل می کند. در زیر تپه بالقوه، ذره دستخوش تغییرات نمایی در دامنه می شود. با در نظر گرفتن رفتار در این محدوده ها و نقاط عطف کلاسیک می توان یک راه حل جهانی ایجاد کرد.
. دور از تپه بالقوه، ذره شبیه به یک موج آزاد و نوسانی عمل می کند. در زیر تپه بالقوه، ذره دستخوش تغییرات نمایی در دامنه می شود. با در نظر گرفتن رفتار در این محدوده ها و نقاط عطف کلاسیک می توان یک راه حل جهانی ایجاد کرد. انتخاب شده است و
انتخاب شده است و در یک سری قدرت در مورد گسترش یافته است
در یک سری قدرت در مورد گسترش یافته است 


![{\displaystyle \Psi (x)=C_{A}Ai\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)+C_{B}Bi\ چپ({\sqrt[{3}]{v_{1}}}(x-x_{1})\راست)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/735a1e9ea0d738f9153e0ceab4ef3171c08a6215)
 و
و هستند
هستند

![{\displaystyle T(E)=e^{-2\int _{x_{1}}^{x_{2}}dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\ چپ[V(x)-E\right]}}}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01314abec4fd51012547a6ee7e4a9ac3813878a0)
 دو نقطه عطف کلاسیک برای مانع بالقوه هستند.
دو نقطه عطف کلاسیک برای مانع بالقوه هستند.







 ثابت پلانک کاهش یافته است،
ثابت پلانک کاهش یافته است،

 تابعی است که انرژی پتانسیل را در هر نقطه x و
تابعی است که انرژی پتانسیل را در هر نقطه x و
 خارج از جعبه، و صفر برای x بین
خارج از جعبه، و صفر برای x بین و
و . تابع موج در نظر گرفته می شود که از تابع موج های مختلف در محدوده های مختلف x تشکیل شده است ، بسته به اینکه x داخل یا خارج جعبه باشد. بنابراین تابع موج به این صورت تعریف می شود:
. تابع موج در نظر گرفته می شود که از تابع موج های مختلف در محدوده های مختلف x تشکیل شده است ، بسته به اینکه x داخل یا خارج جعبه باشد. بنابراین تابع موج به این صورت تعریف می شود:

 معادله می شود
معادله می شود
 از این رو،
از این رو،
 و معادله
و معادله 
 ، و اجازه دادن
، و اجازه دادن


 . اجازه دادن
. اجازه دادن
 که در آن راه حل کلی نمایی است:
که در آن راه حل کلی نمایی است:


 ،
، ، و
، و بودن:
بودن:
 مربوط می شه به
مربوط می شه به ،
، مدت به بی نهایت می رود به همین ترتیب، همانطور که
مدت به بی نهایت می رود به همین ترتیب، همانطور که  ،
، مدت به بی نهایت می رود برای اینکه تابع موج مربعی یکپارچه شود، باید تنظیم کنیم
مدت به بی نهایت می رود برای اینکه تابع موج مربعی یکپارچه شود، باید تنظیم کنیم  ، و ما داریم:
، و ما داریم: و
و




 و
و ، و ضد متقارن، که برای آن
، و ضد متقارن، که برای آن و
و . برای حالت متقارن بدست می آوریم
. برای حالت متقارن بدست می آوریم
 بنابراین گرفتن نسبت می دهد
بنابراین گرفتن نسبت می دهد
 به طور مشابه برای مورد ضد متقارن دریافت می کنیم
به طور مشابه برای مورد ضد متقارن دریافت می کنیم
 وک
وک به انرژی بستگی دارد آنچه ما دریافتیم این است که شرایط تداوم را نمی توان برای مقدار دلخواه انرژی برآورده کرد. زیرا این نتیجه چاه بالقوه نامتناهی است. بنابراین، فقط مقادیر انرژی معینی که راه حل های یکی یا یکی از این دو معادله هستند، مجاز هستند. از این رو متوجه می شویم که سطوح انرژی سیستم زیر
به انرژی بستگی دارد آنچه ما دریافتیم این است که شرایط تداوم را نمی توان برای مقدار دلخواه انرژی برآورده کرد. زیرا این نتیجه چاه بالقوه نامتناهی است. بنابراین، فقط مقادیر انرژی معینی که راه حل های یکی یا یکی از این دو معادله هستند، مجاز هستند. از این رو متوجه می شویم که سطوح انرژی سیستم زیر و
و و توجه داشته باشید از تعاریف
و توجه داشته باشید از تعاریف ، جایی که
، جایی که ، معادلات اصلی خوانده می شود
، معادلات اصلی خوانده می شود
 ، راه حل هایی وجود دارند که در آن نیم دایره آبی منحنی های بنفش یا خاکستری را قطع می کند (
، راه حل هایی وجود دارند که در آن نیم دایره آبی منحنی های بنفش یا خاکستری را قطع می کند ( و-
و- ). هر منحنی بنفش یا خاکستری نشان دهنده یک راه حل ممکن است،
). هر منحنی بنفش یا خاکستری نشان دهنده یک راه حل ممکن است، در محدوده
در محدوده . تعداد کل راه حل ها،ن
. تعداد کل راه حل ها،ن ، (یعنی تعداد منحنی های بنفش/خاکستری که با دایره آبی قطع می شوند) بنابراین با تقسیم شعاع دایره آبی تعیین می شود.
، (یعنی تعداد منحنی های بنفش/خاکستری که با دایره آبی قطع می شوند) بنابراین با تقسیم شعاع دایره آبی تعیین می شود. با محدوده هر راه حل
با محدوده هر راه حل و با استفاده از توابع کف یا سقف:
و با استفاده از توابع کف یا سقف: 
 .
.
 و�3=3.73
و�3=3.73 ، با انرژی های مربوطه
، با انرژی های مربوطه اگر بخواهیم می توانیم به عقب برگردیم و مقادیر ثابت ها را پیدا کنیمآ،ب،جی،اچ
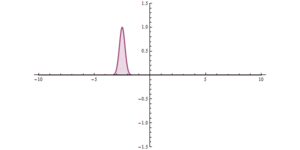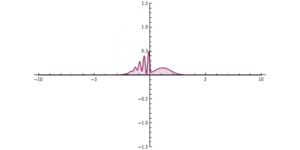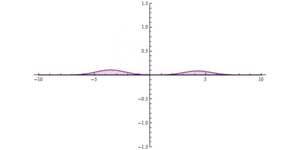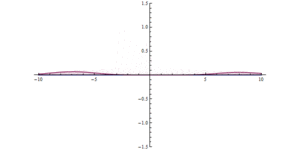
اگر بخواهیم می توانیم به عقب برگردیم و مقادیر ثابت ها را پیدا کنیمآ،ب،جی،اچ اکنون در معادلات (ما همچنین باید شرایط عادی سازی را اعمال کنیم). در سمت راست سطوح انرژی و توابع موج را در این مورد نشان میدهیم (جایی که
اکنون در معادلات (ما همچنین باید شرایط عادی سازی را اعمال کنیم). در سمت راست سطوح انرژی و توابع موج را در این مورد نشان میدهیم (جایی که ):
): ، شعاع نیم دایره بزرگتر می شود و ریشه ها به مقادیر نزدیک و نزدیکتر می شوند.
، شعاع نیم دایره بزرگتر می شود و ریشه ها به مقادیر نزدیک و نزدیکتر می شوند. ، و مورد
، و مورد  با�0�
با�0� درست شد. مانندتو0∝�0�
درست شد. مانندتو0∝�0� به سمت صفر میل خواهد کرد و بنابراین فقط یک حالت محدود وجود خواهد داشت. راه حل تقریبی پس از آن است�2=تو02-تو04
به سمت صفر میل خواهد کرد و بنابراین فقط یک حالت محدود وجود خواهد داشت. راه حل تقریبی پس از آن است�2=تو02-تو04 ، و انرژی تمایل دارد�=-متر�2�02/2ℏ2
، و انرژی تمایل دارد�=-متر�2�02/2ℏ2 . اما این فقط انرژی حالت محدود یک
. اما این فقط انرژی حالت محدود یک  . مقادیر نرمال شده هستند
. مقادیر نرمال شده هستند ارتباط مستقیم بین زوجین مجاز را بیان می کند
ارتباط مستقیم بین زوجین مجاز را بیان می کند همانطور که
همانطور که  به ترتیب برای توابع موج برابری زوج و فرد. در معادلات قبلی فقط قسمت های مشتق مثبت توابع باید در نظر گرفته شوند. نمودار به طور مستقیم زوج های مجاز را نشان می دهد
به ترتیب برای توابع موج برابری زوج و فرد. در معادلات قبلی فقط قسمت های مشتق مثبت توابع باید در نظر گرفته شوند. نمودار به طور مستقیم زوج های مجاز را نشان می دهد

 . راه حل مربوطه برای تابع موج با
. راه حل مربوطه برای تابع موج با پیدا شده است
پیدا شده است

 یک بار تعیین می شوند
یک بار تعیین می شوند
 وجود معادله ریشه به بالا همیشه تضمین شده نیست، به عنوان مثال، همیشه می توان مقداری از آن را پیدا کردآ
وجود معادله ریشه به بالا همیشه تضمین شده نیست، به عنوان مثال، همیشه می توان مقداری از آن را پیدا کردآ آنقدر کوچک است که برای مقادیر داده شده از
آنقدر کوچک است که برای مقادیر داده شده از و
و ، هیچ سطح انرژی گسسته ای وجود ندارد. نتایج چاه متقارن از معادله بالا با تنظیم به دست می آید
، هیچ سطح انرژی گسسته ای وجود ندارد. نتایج چاه متقارن از معادله بالا با تنظیم به دست می آید .
.

 قسمت شعاعی تابع موج است. توجه کنید که برای (n = 1) قسمت زاویه ای ثابت است (ℓ = 0).
قسمت شعاعی تابع موج است. توجه کنید که برای (n = 1) قسمت زاویه ای ثابت است (ℓ = 0).








 می خواند
می خواند![{\displaystyle {\hat {H}}\psi (x)=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2 }}}+V(x)\right]\psi (x)=E\psi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cebcb7b8c2a842aa74465b47f55d8dc936341e5) جایی که
جایی که
![{\displaystyle V(x)=V_{0}[\Theta (x)-\Theta (xa)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b52afbe20b051bc09bfcb26c46de6c0d52269b) پتانسیل مانع با ارتفاع است
پتانسیل مانع با ارتفاع است و عرض
و عرض 

 و
و . مانع را می توان به هر کدام منتقل کردایکس
. مانع را می توان به هر کدام منتقل کردایکس انرژی جنبشی است.
انرژی جنبشی است. ). در هر یک از این بخش ها، پتانسیل ثابت است، به این معنی که ذره شبه آزاد است و حل معادله شرودینگر را می توان به صورت برهم نهی از
). در هر یک از این بخش ها، پتانسیل ثابت است، به این معنی که ذره شبه آزاد است و حل معادله شرودینگر را می توان به صورت برهم نهی از 

 روی ضرایبآ
روی ضرایبآ وب
وب جهت بردار سرعت را نشان می دهد. توجه داشته باشید که اگر انرژی ذره کمتر از ارتفاع سد باشد،
جهت بردار سرعت را نشان می دهد. توجه داشته باشید که اگر انرژی ذره کمتر از ارتفاع سد باشد، خیالی می شود و تابع موج به صورت تصاعدی در داخل مانع در حال فروپاشی است. با این وجود، ما علامت گذاری را حفظ می کنیم
خیالی می شود و تابع موج به صورت تصاعدی در داخل مانع در حال فروپاشی است. با این وجود، ما علامت گذاری را حفظ می کنیم . مورد
. مورد در زیر درمان می شود.
در زیر درمان می شود. باید از
باید از 









 ). ممکن است منعکس شود (
). ممکن است منعکس شود ( ) یا منتقل شده (
) یا منتقل شده ( ).
). (ذره ورودی)،
(ذره ورودی)، (انعکاس)
(انعکاس) (بدون ذره ورودی از سمت راست)، و
(بدون ذره ورودی از سمت راست)، و (انتقال). سپس ضرایب را حذف می کنیم
(انتقال). سپس ضرایب را حذف می کنیم از معادله و حل کنید
از معادله و حل کنید و
و .
.

 ،
،  ، بنابراین در هر دوی این عبارات یک تکینگی وجود دارد.
، بنابراین در هر دوی این عبارات یک تکینگی وجود دارد.
 = 7. خط چین: نتیجه کلاسیک. خط جامد: نتیجه مکانیک کوانتومی
= 7. خط چین: نتیجه کلاسیک. خط جامد: نتیجه مکانیک کوانتومی
 . این اثر که با حالت کلاسیک متفاوت است،
. این اثر که با حالت کلاسیک متفاوت است،  ، در حالی که در داخل مانع به طور تصاعدی در طول یک فاصله میرا می شود
، در حالی که در داخل مانع به طور تصاعدی در طول یک فاصله میرا می شود . اگر مانع بسیار گستردهتر از این طول پوسیدگی باشد، قسمت چپ و راست عملاً مستقل هستند و در نتیجه تونلزنی سرکوب میشود.
. اگر مانع بسیار گستردهتر از این طول پوسیدگی باشد، قسمت چپ و راست عملاً مستقل هستند و در نتیجه تونلزنی سرکوب میشود.
 .
.
 . نتیجه کلاسیک انتقال کامل بدون هیچ بازتابی (
. نتیجه کلاسیک انتقال کامل بدون هیچ بازتابی ( ،
، ) نه تنها در حد انرژی بالا بازتولید می شود
) نه تنها در حد انرژی بالا بازتولید می شود اما همچنین زمانی که انرژی و عرض مانع برآورده می شود
اما همچنین زمانی که انرژی و عرض مانع برآورده می شود ، جایی که،…
، جایی که،… (به قله های نزدیک مراجعه کنید
(به قله های نزدیک مراجعه کنید و 1.8 در شکل بالا). توجه داشته باشید که احتمالات و دامنه های نوشته شده برای هر انرژی (بالا/زیر) ارتفاع مانع است.
و 1.8 در شکل بالا). توجه داشته باشید که احتمالات و دامنه های نوشته شده برای هر انرژی (بالا/زیر) ارتفاع مانع است.
 .
. در حین نگهداری
در حین نگهداری ثابت.
ثابت.
![{\displaystyle {\hat {H}}\psi (x)=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2 }}}+V(x)\right]\psi (x)=E\psi (x)،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5da2645c6d41085b01458a55a9580b088983c178)





 .
.








 .
.

 ، که k عدد موج ذره است.
، که k عدد موج ذره است. 






















 انرژی سیستم مکانیکی مربوطه، طبق تعریف ،
انرژی سیستم مکانیکی مربوطه، طبق تعریف ،
 انرژی تحت تغییرات مختصات فضای پیکربندی ثابت است
انرژی تحت تغییرات مختصات فضای پیکربندی ثابت است ، یعنی
، یعنی
 به عنوان ضرایب یک فرم خطی تغییر می کند.
به عنوان ضرایب یک فرم خطی تغییر می کند. به صراحت به زمان بستگی ندارد. قانون بقای انرژی بیان می کند که انرژی
به صراحت به زمان بستگی ندارد. قانون بقای انرژی بیان می کند که انرژی افراطی بودن . (به عبارت دیگر،
افراطی بودن . (به عبارت دیگر، معادلات اویلر-لاگرانژ را برآورده می کند). در نظر گرفتن کل مشتق زمانی از
معادلات اویلر-لاگرانژ را برآورده می کند). در نظر گرفتن کل مشتق زمانی از![{\displaystyle -{\frac {\partial L}{\partial t}}{\biggl |}_{\mathbf {q} (t)}={\frac {\mathrm {d} }{\mathrm {d } t}}\left[E{\biggl |}_{\mathbf {q} (t)}\راست].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8bb04875cb2c57a1ce578378edae29d1f1797)
 بنابراین
بنابراین



















 از عمودی مختصات و مولفه های سرعت آونگ باب هستند
از عمودی مختصات و مولفه های سرعت آونگ باب هستند


![{\displaystyle {\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1 {2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right ){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^ {2}{\dot {\theta }}^{2}+mg\ell \cos \theta \,.\end{آرایه}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcea9ca5dd9452880b94f4315f2430d4f9c88684)


![\frac{\mathrm{d}}{\mathrm{d}t}\left[ m( \dot x \ell \cos\theta + \ell^2 \dot\theta ) \right] + m \ell (\ نقطه x \dot \theta + g) \sin\theta = 0;](https://wikimedia.org/api/rest_v1/media/math/render/svg/27ef95240aa335e09f85c8c7ef67a7301547c588)

 باید معادلات حرکت یک آونگ ساده را که در یک قاب اینرسی ساکن است ، ارائه دهد ، در حالی که¨→0
باید معادلات حرکت یک آونگ ساده را که در یک قاب اینرسی ساکن است ، ارائه دهد ، در حالی که¨→0 باید معادلات یک آونگ در یک سیستم دائماً شتابدهنده و غیره را ارائه دهد. علاوه بر این، با توجه به شرایط شروع مناسب و یک گام زمانی انتخابی، با گام برداشتن از نتایج به صورت تکراری، به دست آوردن نتایج به صورت عددی امری بیاهمیت است .
باید معادلات یک آونگ در یک سیستم دائماً شتابدهنده و غیره را ارائه دهد. علاوه بر این، با توجه به شرایط شروع مناسب و یک گام زمانی انتخابی، با گام برداشتن از نتایج به صورت تکراری، به دست آوردن نتایج به صورت عددی امری بیاهمیت است .






![{\displaystyle [t_{\text{st}},t_{\text{fin}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a944afffe8a6ed04da84668c122a86910bb9708c) و نقاط پایانی ثابت
و نقاط پایانی ثابت  و
و ، سپس دو لاگرانژی که یک سیستم را توصیف می کنند می توانند با "مشتق زمان کل" یک تابع متفاوت باشند.
، سپس دو لاگرانژی که یک سیستم را توصیف می کنند می توانند با "مشتق زمان کل" یک تابع متفاوت باشند. : [29]
: [29]
 به معنای
به معنای
 معادلات حرکتی یکسان [30] [31] از اعمال مربوطه را تولید می کنداس
معادلات حرکتی یکسان [30] [31] از اعمال مربوطه را تولید می کنداس واس"
واس" از طریق مرتبط هستند
از طریق مرتبط هستند![{\displaystyle {\begin{aligned}S'[\mathbf {q} ]=\int \limits _{t_{\text{st}}}^{t_{\text{fin}}}L'(\mathbf {q} (t)،{\dot {\mathbf {q} }}(t)،t)\,dt=\int \limits _{t_{\text{st}}}^{t_{\text{ fin}}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt+\int _{t_{\text{st}}}^{ t_{\text{fin}}}{\frac {\mathrm {d} f(\mathbf {q} (t),t)}{\mathrm {d} t}}\,dt\\=S[\ mathbf {q} ]+f(P_{\text{fin}},t_{\text{fin}})-f(P_{\text{st}},t_{\text{st}}),\end {هم راستا}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18afb93a0e579c8b88bf8564811c4f9437e22d33)
 و
و مستقل از.
مستقل از.






![{\displaystyle \int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _ {j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\mathrm {d} }{\mathrm { d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)-{\frac {\mathrm {d } }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)\,\mathrm {d } t\,=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j} \right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({ \frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,\mathrm {d} t\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54a48053647f191bd378c62f02e1dc5e53fdfb4e)













![{\displaystyle \sum _{j=1}^{n}\left[Q_{j}-\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\ T جزئی {\ جزئی {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}= 0\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf81ebf14cb6b43779228e274d39444e1a4d7787)


 انرژی جنبشی کل سیستم، برابر با مجموع Σ انرژی جنبشی ذرات است، [5] و V انرژی پتانسیل سیستم است .
انرژی جنبشی کل سیستم، برابر با مجموع Σ انرژی جنبشی ذرات است، [5] و V انرژی پتانسیل سیستم است .

 ، فقط است
، فقط است ; برای ارتباط دادن مولفه سرعت به مختصات مربوطه z 2 نیازی به استفاده از قوانین زنجیره نامناسب یا مشتقات کل نیست .
; برای ارتباط دادن مولفه سرعت به مختصات مربوطه z 2 نیازی به استفاده از قوانین زنجیره نامناسب یا مشتقات کل نیست .

 .
.







 متشکل از یک فضای پیکربندی
متشکل از یک فضای پیکربندی  و عملکرد صاف
و عملکرد صاف درون آن فضایی که لاگرانژی نامیده می شود . برای بسیاری از سیستم
درون آن فضایی که لاگرانژی نامیده می شود . برای بسیاری از سیستم  جایی که
جایی که و
و به ترتیب انرژی جنبشی و پتانسیل سیستم هستند . [2]
به ترتیب انرژی جنبشی و پتانسیل سیستم هستند . [2]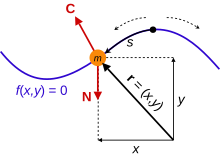

 در مکانیک نیوتنی، معادلات حرکت با قوانین نیوتن ارائه می شود . قانون دوم " نیروی خالص برابر است با جرم ضربدر شتاب ".
در مکانیک نیوتنی، معادلات حرکت با قوانین نیوتن ارائه می شود . قانون دوم " نیروی خالص برابر است با جرم ضربدر شتاب ". برای هر ذره اعمال می شود. برای یک سیستم ذرات N در 3 بعد، معادلات دیفرانسیل معمولی 3 N مرتبه دوم در موقعیتهای ذرات وجود دارد که باید حل شوند.
برای هر ذره اعمال می شود. برای یک سیستم ذرات N در 3 بعد، معادلات دیفرانسیل معمولی 3 N مرتبه دوم در موقعیتهای ذرات وجود دارد که باید حل شوند.


 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.