همبستگی (پیرسون ، کندال ، اسپیرمن)
فهرست تجزیه و تحلیل آماری همبستگی (پیرسون ، کندال ، اسپیرمن)
همبستگی (پیرسون ، کندال ، اسپیرمن)
همبستگی یک تحلیل دو متغیره است که قدرت ارتباط بین دو متغیر و جهت رابطه را اندازه گیری می کند. از نظر قدرت رابطه ، مقدار ضریب همبستگی بین 1+ و -1 تغییر می کند. مقدار 1 ± نشان دهنده درجه كامل ارتباط بین دو متغیر است. هرچه مقدار ضریب همبستگی به سمت 0 می رود ، رابطه بین دو متغیر ضعیف تر خواهد بود. جهت رابطه با علامت ضریب نشان داده می شود. علامت + نشان دهنده یک رابطه مثبت و علامت - یک رابطه منفی است. معمولاً در آمار ، چهار نوع همبستگی را اندازه گیری می کنیم: همبستگی پیرسون، همبستگی رتبه کندال ، همبستگی اسپیرمن و همبستگی نقطه ای-دوقلویی. نرم افزار زیر به شما امکان می دهد خیلی راحت یک همبستگی را انجام دهید.
R همبستگی پیرسون: پیرسون r و همبستگی آماری همبستگی به طور گسترده استفاده برای اندازه گیری درجه از رابطه بین متغیرهای خطی مربوط است. برای مثال، در بازار سهام، اگر ما می خواهیم برای اندازه گیری چگونه دو سهم مربوط به هر یک از دیگر، پیرسون r و همبستگی برای اندازه گیری میزان ارتباط بین دو استفاده شده است. همبستگی نقطه به نقطه با فرمول همبستگی پیرسون انجام می شود با این تفاوت که یکی از متغیرها دوگانه است. از فرمول زیر استفاده می شود برای محاسبه پیرسون r و همبستگی:
r xy = ضریب همبستگی پیرسون r بین x و y
n = تعداد مشاهدات
x i = مقدار x (برای هر مشاهده)
y i = مقدار y (برای هر مشاهده)
انواع سوالات تحقیق که یک همبستگی پیرسون می تواند بررسی کند:
آیا از نظر آماری بین سن ، اندازه گیری شده در سال و قد ، اندازه گیری شده در اینچ رابطه معنی داری وجود دارد؟
آیا بین دمای اندازه گیری شده بر حسب درجه فارنهایت و فروش بستنی رابطه ای وجود دارد که بر اساس درآمد اندازه گیری می شود؟
آیا رابطه ای بین رضایت شغلی ، اندازه گیری شده توسط JSS و درآمد ، اندازه گیری شده بر حسب دلار وجود دارد؟
فرضیات
برای همبستگی پیرسون r ، هر دو متغیر باید به طور معمول توزیع شوند (متغیرهای توزیع شده به طور معمول دارای یک منحنی زنگوله ای هستند). فرضیات دیگر شامل خطی بودن و همدلی بودن است. خطی بودن فرض می کند که یک رابطه مستقیم بین هر یک از دو متغیر وجود دارد و هموسدیستی بودن فرض می کند که داده ها به طور مساوی در مورد خط رگرسیون توزیع شده اند.
همبستگی پیرسون را انجام دهید و آن را تفسیر کنید
شرایط کلیدی
اندازه اثر: از استاندارد کوهن برای ارزیابی ضریب همبستگی برای تعیین قدرت رابطه یا اندازه اثر ممکن است استفاده شود. ضرایب همبستگی بین .10 و .29 نشان دهنده یک ارتباط کوچک ، ضرایب بین 0.30 و .49 نمایانگر یک ارتباط متوسط است و ضرایب 0.50 به بالا یک ارتباط یا رابطه بزرگ را نشان می دهد.
داده های مداوم: داده هایی که فاصله یا سطح نسبت دارند. این نوع داده دارای خصوصیات اندازه و فواصل برابر بین واحدهای مجاور است. فواصل برابر بین واحدهای مجاور به معنای وجود مقادیر مساوی از متغیر اندازه گیری شده بین واحدهای مجاور در مقیاس است. یک مثال می تواند سن باشد. افزایش سن از 21 به 22 همان افزایش سن از 60 به 61 سال خواهد بود.
همبستگی رتبه کندال : همبستگی رتبه کندال یک آزمون غیر پارامتری است که قدرت وابستگی بین دو متغیر را اندازه گیری می کند. اگر دو نمونه a و b را در نظر بگیریم که اندازه نمونه n باشد ، می دانیم که تعداد کل جفت شدن های ab n ( n -1) / 2 است . برای محاسبه مقدار همبستگی رتبه کندال از فرمول زیر استفاده شده است:
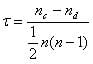
Nc = تعداد
ناسازگار Nd = تعداد ناسازگار
همبستگی کندال را انجام دهید و آن را تفسیر کنید
شرایط کلیدی
سازگار: به همین ترتیب سفارش داده شده است.
ناسازگار: متفاوت سفارش داده شده است.
همبستگی رتبه Spearman : همبستگی رتبه Spearman یک آزمون غیر پارامتری است که برای اندازه گیری میزان ارتباط بین دو متغیر استفاده می شود. آزمون همبستگی رتبه Spearman هیچ فرضی در مورد توزیع داده ها ندارد و هنگامی که متغیرها در مقیاس حداقل ترتیبی اندازه گیری می شوند ، تحلیل همبستگی مناسب است.
برای محاسبه همبستگی رتبه Spearman از فرمول زیر استفاده شده است:
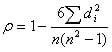
ρ = همبستگی رتبه Spearman
di = اختلاف بین صفات متغیرهای مربوطه
n = تعداد مشاهدات
انواع سوالات تحقیقاتی که همبستگی اسپیرمن می تواند بررسی کند:
آیا از نظر آماری بین سطح تحصیلات شرکت کنندگان (دبیرستان ، لیسانس یا تحصیلات تکمیلی) و حقوق اولیه آنها رابطه معناداری وجود دارد؟
آیا از نظر آماری بین موقعیت اتمام اسب و نژاد رابطه معنی داری وجود دارد؟
فرضیات
مفروضات همبستگی اسپیرمن این است که داده ها باید حداقل ترتیبی باشند و امتیازات یک متغیر باید به صورت یکنواخت با متغیر دیگر مرتبط باشد.
همبستگی Spearman را انجام دهید و آن را تفسیر کنید
شرایط کلیدی
اندازه اثر: از استاندارد کوهن برای ارزیابی ضریب همبستگی برای تعیین قدرت رابطه یا اندازه اثر ممکن است استفاده شود. ضرایب همبستگی بین .10 و .29 نشان دهنده یک ارتباط کوچک ، ضرایب بین 0.30 و .49 نمایانگر یک ارتباط متوسط است و ضرایب 0.50 به بالا یک ارتباط یا رابطه بزرگ را نشان می دهد.
داده های عادی: در یک مقیاس ترتیبی ، سطوح یک متغیر به گونه ای مرتب می شوند که بتوان یک سطح را از سطح دیگر بالاتر / پایین تر در نظر گرفت. با این حال ، لزوماً اختلاف اختلاف بین سطوح مشخص نیست. به عنوان مثال می توان به درجه بندی سطح تحصیلات اشاره کرد. مدرک تحصیلات تکمیلی بالاتر از لیسانس است و لیسانس بالاتر از دیپلم دبیرستان. با این حال ، ما نمی توانیم میزان تحصیلات تکمیلی بالاتر را با مقطع کارشناسی مقایسه کنیم. همچنین نمی توانیم بگوییم که تفاوت تحصیلات در مقطع تحصیلات تکمیلی و کارشناسی همان تفاوت بین مدرک لیسانس و دیپلم دبیرستان است.
منابع همبستگی:
Algina، J.، & Keselman، HJ (1999). مقایسه ضرایب همبستگی چندگانه مجذور: بررسی یک فاصله اطمینان و اهمیت آزمون. روشهای روانشناختی ، 4 (1) ، 76-83.
Bobko ، P. (2001). همبستگی و رگرسیون: کاربردهایی برای روانشناسی و مدیریت سازمانی صنعتی (ویرایش دوم). هزار اوکس ، کالیفرنیا: انتشارات سیج. چشم انداز
بونت ، DG (2008). برآورد فاصله متاآنالیز برای همبستگی های متغیر روشهای روانشناختی ، 13 (3) ، 173-181.
چن ، PY و پوپویچ ، PM (2002). همبستگی: معیارهای پارامتری و غیرپارامتری . هزار اوکس ، کالیفرنیا: انتشارات سیج. چشم انداز
Cheung، MW -L.، & Chan، W. (2004). آزمایش ضرایب همبستگی وابسته از طریق مدل سازی معادلات ساختاری . روشهای تحقیق سازمانی ، 7 (2) ، 206-223.
Coffman، DL، Maydeu-Olivares، A.، Arnau، J. (2008). تخمین فاصله آزاد توزیع مجانبی: برای ضریب همبستگی درون کلاس با کاربردها در داده های طولی. روش شناسی ، 4 (1) ، 4-9.
کوهن ، ج. ، کوهن ، پی. ، وست ، SG ، و آیکن ، LS (2003). تحلیل رگرسیون / همبستگی چندگانه برای علوم رفتاری . (ویرایش سوم). مهوا ، نیوجرسی: همکاران لارنس ارلباوم. چشم انداز
Hatch، JP، Hearne، EM، & Clark، GM (1982). روشی برای آزمون همبستگی سریال در تجزیه و تحلیل واریانس اندازه گیری های تکراری متغیر. روش تحقیق و ابزار دقیق رفتار ، 14 (5) ، 497-498.
کندال ، ام جی و گیبونز ، جی دی (1990). روشهای همبستگی رتبه (ویرایش پنجم). لندن: ادوارد آرنولد. چشم انداز
Krijnen ، WP (2004). بارهای مثبت و ضرایب همبستگی از ماتریس های کوواریانس مثبت روان سنجی ، 69 (4) ، 655-660.
شیعه ، جی. (2006). برآورد دقیق زمان ، محاسبه توان و تعیین اندازه نمونه در تحلیل همبستگی نرمال. روان سنجی ، 71 (3) ، 529-540.
Stauffer ، JM ، و Mendoza ، JL (2001). توالی مناسب برای اصلاح ضرایب همبستگی برای محدودیت دامنه و عدم اطمینان. روان سنجی ، 66 (1) ، 63-68.
صفحات مرتبط:
- جدول مقادیر بحرانی: همبستگی پیرسون
- همبستگی رتبه Spearman را انجام دهید و آن را تفسیر کنید
- همبستگی دو متغیره (پیرسون) را انجام دهید و آن را تفسیر کنید
https://www.statisticssolutions.com/free-resources/directory-of-statistical-analyses/correlation-pearson-kendall-spearman/
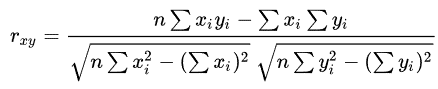
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.