ریاضیات

Kendall's Tau nn این ضریب است که برای اندازه گیری ارتباط بین دو جفت داده رتبه بندی شده استفاده می شود. این نام به نام موریس کندال ، آمارشناس انگلیسی است که آن را در سال 1938 توسعه داده است. 0 تا 1. 0 Tau-a (بدون کراوات) و Tau-b (با کراوات) 87

فرمول Tau-a n 88

ناسازگار و ناسازگار n 89

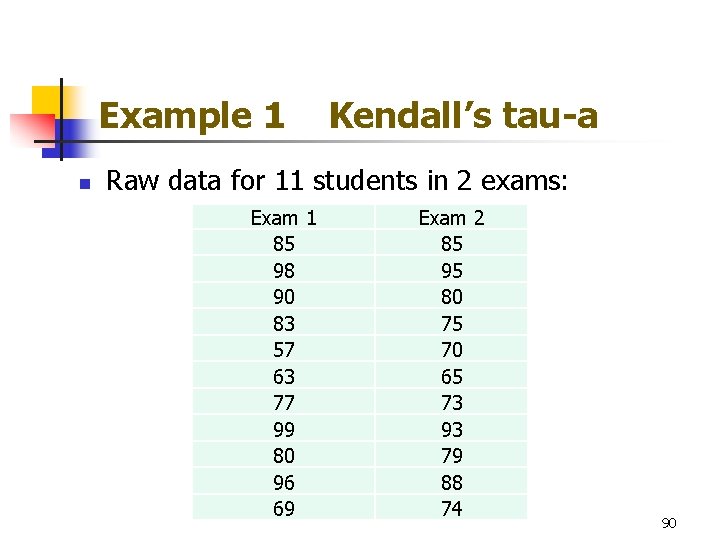
مثال 1 داده های خام کندال برای 11 دانشجو در 2 آزمون: آزمون 1 85 98 90 83 57 63 77 99 80 96 69 آزمون 1 85 95 80 75 70 65 73 93 93 79 88 74 90

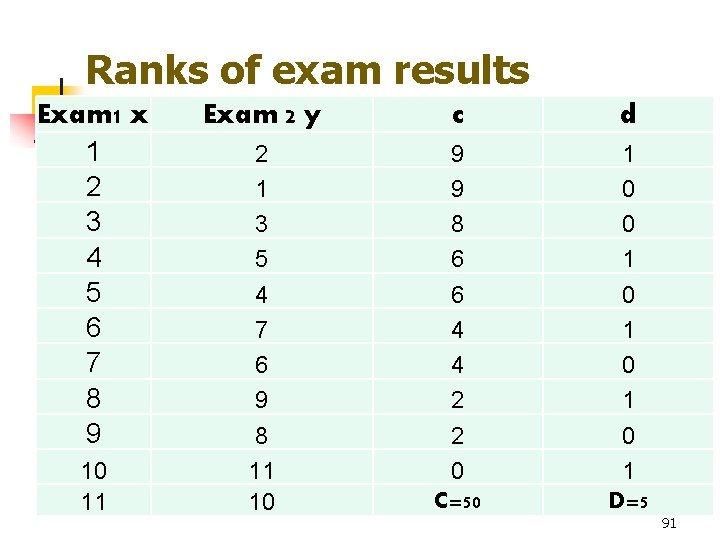
رتبه های نتایج آزمون 1 x 1 2 3 4 5 6 7 8 9 10 11 آزمون 2 ycd 2 1 3 5 4 7 6 9 8 11 10 9 9 8 8 6 6 4 4 2 2 0 C = 50 1 0 1 0 1 91 = D = 5

محاسبه برای ṫ n 92

مراحل محاسبه ṫ 1. مرتب سازی داده ها x به ترتیب صعودی ، جفت y با x 2. مرتبه را برای هر y بشمارید 3. جمع C و D 3. جمع C و D 4. برای محاسبه 93 formula از فرمول استفاده کنید

فرمول tau-b (با کراوات) n 94

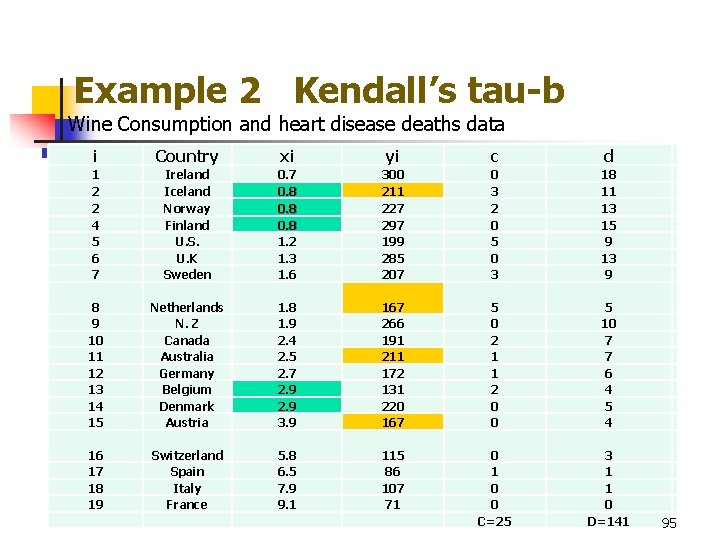
مثال 2 Kendall's tau-b شراب مصرف و بیماری های قلبی داده های مرگ من کشور xi yi cd 1 2 2 4 5 6 7 ایرلند ایسلند نروژ فنلاند USU K سوئد 0. 7 0. 8 1. 2 1. 3 1. 6 300 211 227 297 199 285 207 0 3 2 0 5 0 3 18 11 13 15 9 13 9 8 9 10 11 12 13 14 15 هلند N. Z کانادا استرالیا آلمان بلژیک دانمارک اتریش 1. 8 1. 9 2. 4 2. 5 2. 7 2. 9 3. 9 167 266 191 211 172 131 220 167 5 0 2 1 1 2 0 0 5 10 7 7 6 4 5 4 16 17 18 19 سوئیس اسپانیا ایتالیا فرانسه 5. 8 6. 5 7. 9 9. 1 115 86 107 71 0 0 C = 25 3 1 1 0 D = 141 95

محاسبه tau-b n 96

آزمون فرضیه برای τ n 97

نتایج آزمون فرضیه n 98

https://slidetodoc.com/nonparametric-statistical-methods-presented-by-guo-cheng-ning/