تعریف روش رگرسیون حداقل مربعات
روش رگرسیون حداقل مربعات شکلی از تحلیل رگرسیونی است که رابطه بین متغیر وابسته و مستقل را همراه با یک خط خطی ایجاد می کند. این خط به عنوان "خط بهترین تناسب" نامیده می شود.
تحلیل رگرسیون یک روش آماری است که به کمک آن می توان مقادیر مجهول یک متغیر را از مقادیر شناخته شده متغیر دیگر تخمین زد یا پیش بینی کرد. متغیری که برای پیشبینی علاقه متغیر استفاده میشود، متغیر مستقل یا توضیحی نامیده میشود و متغیری که پیشبینی میشود، متغیر وابسته یا تبیینشده نامیده میشود.
اجازه دهید دو متغیر x و y را در نظر بگیریم. اینها بر روی یک نمودار با مقادیر x در مقادیر محور x از y در محور y رسم می شوند. این مقادیر با نقاط در نمودار زیر نشان داده شده است. یک خط مستقیم از میان نقاط کشیده میشود - به آن خط بهترین تناسب گفته میشود.
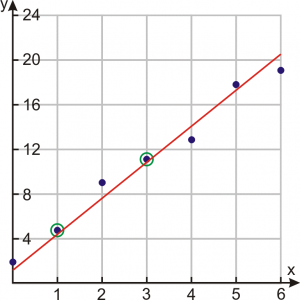
هدف از رگرسیون حداقل مربعات این است که اطمینان حاصل شود که خط ترسیم شده از طریق مجموعه مقادیر ارائه شده نزدیکترین رابطه را بین مقادیر ایجاد می کند.
فرمول رگرسیون حداقل مربعات
خط رگرسیون تحت روش حداقل مربعات با استفاده از فرمول زیر محاسبه می شود:
ŷ = a + bx

شما می توانید از این تصویر در وب سایت خود، قالب ها و غیره استفاده کنید،لطفاً یک پیوند انتساب به ما ارائه دهید
جایی که،
- ŷ = متغیر وابسته
- x = متغیر مستقل
- a = y-برق
- b = شیب خط
شیب خط b با استفاده از فرمول زیر محاسبه می شود:
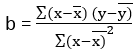
یا
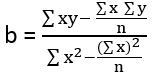
مقطع Y، 'a' با استفاده از فرمول زیر محاسبه می شود -
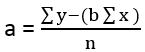
خط بهترین تناسب در رگرسیون حداقل مربع
درخط بهترین تناسبیک خط مستقیم است که از طریق پراکنده ای از نقاط داده کشیده شده است که به بهترین نحو نشان دهنده رابطه بین آنها است.
اجازه دهید نمودار زیر را در نظر بگیریم که در آن مجموعه ای از داده ها در امتداد محور x و y رسم شده است. این نقاط داده با استفاده از نقاط آبی نشان داده می شوند. سه خط از میان این نقاط کشیده می شود - یک خط سبز، یک خط قرمز و یک خط آبی. خط سبز از یک نقطه و خط قرمز از سه نقطه داده می گذرد. با این حال، خط آبی از چهار نقطه داده عبور می کند و فاصله بین نقاط باقیمانده تا خط آبی در مقایسه با دو خط دیگر حداقل است.
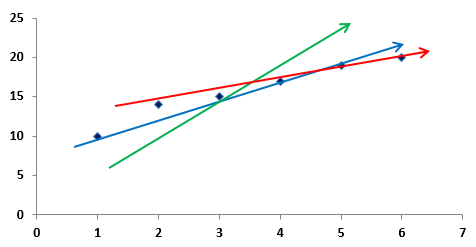
در نمودار بالا، خط آبی نشاندهنده خط بهترین تناسب است زیرا به تمام مقادیر نزدیکتر است و فاصله بین نقاط خارج از خط تا خط حداقل است (یعنی فاصله بین باقیماندهها تا خط بهترین تناسب - همچنین به عنوان مجموع مربعات باقیمانده نامیده می شود). در دو خط دیگر، نارنجی و سبز، فاصله بین باقیمانده ها تا خطوط در مقایسه با خط آبی بیشتر است.
روش حداقل مربعات نزدیکترین رابطه را بین وابسته ومتغیرهای مستقلبا به حداقل رساندن فاصله بین باقیمانده ها، و خط بهترین تناسب، به عنوان مثال، مجموع مربعات باقیمانده در این روش حداقل است. از این رو اصطلاح "کمترین مربع" به وجود می آید.
نمونه هایی از خط رگرسیون حداقل مربعات
اجازه دهید این فرمول ها را در سوال زیر اعمال کنیم -
شما می توانید این قالب اکسل رگرسیون حداقل مربعات را از اینجا دانلود کنید – قالب اکسل رگرسیون حداقل مربعات
مثال شماره 1
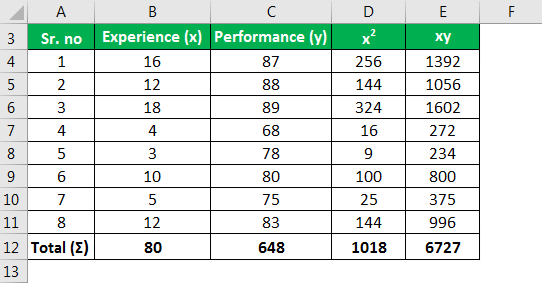
جزئیات مربوط به تجربه تکنسین ها در یک شرکت (در چند سال) و رتبه عملکرد آنها در جدول زیر ارائه شده است. با استفاده از این مقادیر، رتبه عملکرد را برای یک تکنسین با 20 سال تجربه تخمین بزنید.
| تجربه تکنسین (در سال) | رتبه بندی عملکرد |
|---|---|
| 16 | 87 |
| 12 | 88 |
| 18 | 89 |
| 4 | 68 |
| 3 | 78 |
| 10 | 80 |
| 5 | 75 |
| 12 | 83 |
راه حل -
برای محاسبه حداقل مربعات، ابتدا مقطع Y (a) و شیب یک خط (b) را به صورت زیر محاسبه می کنیم:
شیب خط (ب)
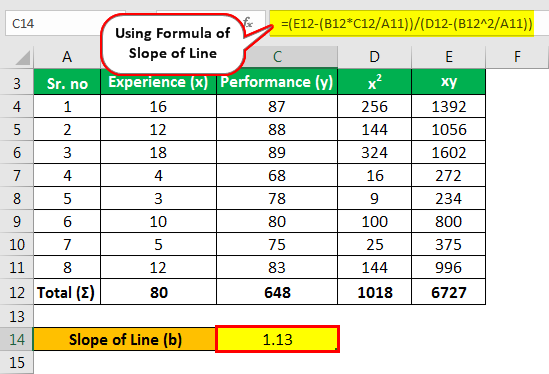
- b = 6727 - [(80*648)/8] / 1018 - [(80) 2/8 ]
- = 247/218
- = 1.13
قطع Y (a)
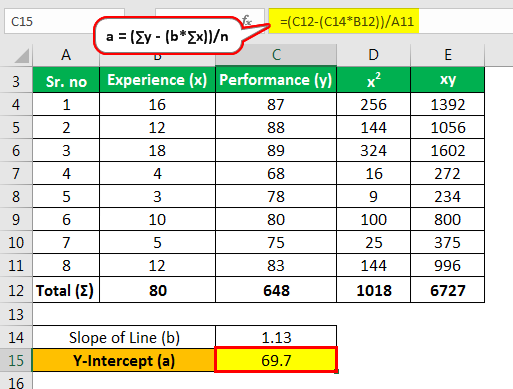
- a = 648 - (1.13) (80) /8
- = 69.7
خط رگرسیون به صورت زیر محاسبه می شود:
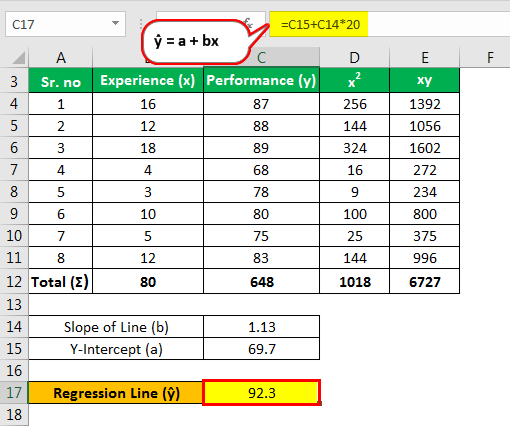
جایگزینی 20 به جای مقدار x در فرمول،
- ŷ = a + bx
- ŷ = 69.7 + (1.13) (20)
- ŷ = 92.3
امتیاز عملکرد برای یک تکنسین با 20 سال سابقه، 92.3 برآورد شده است.
مثال شماره 2
معادله رگرسیون حداقل مربعات با استفاده از اکسل
معادله رگرسیون حداقل مربعات را می توان با استفاده از اکسل با مراحل زیر محاسبه کرد:
- درج کنیدجدول داده ها در اکسل.
- یک نمودار پراکندگی با استفاده از نقاط داده درج کنید.
- یک خط روند را در نمودار پراکندگی درج کنید.
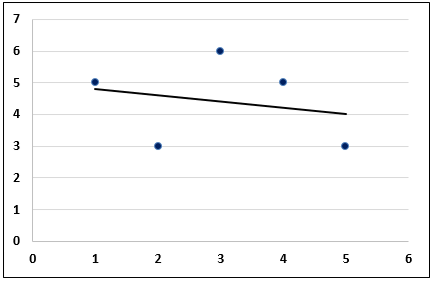
- در زیر گزینه های خط روند - خط روند خطی را انتخاب کنید و معادله نمایش را در نمودار انتخاب کنید.
- معادله رگرسیون حداقل مربعات برای مجموعه داده شده اکسل روی نمودار نمایش داده می شود.
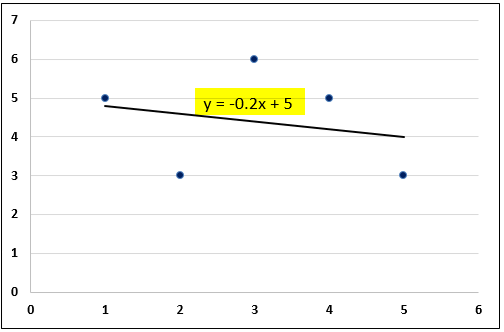
بنابراین، معادله رگرسیون حداقل مربعات برای مجموعه دادههای اکسل محاسبه میشود. با استفاده از معادله، پیش بینی ها و تحلیل روند ممکن است ساخته شود. ابزارهای اکسل نیز محاسبات رگرسیون دقیق را فراهم می کنند.
مزایای
- روش حداقل مربعات تحلیل رگرسیون برای مدلهای پیشبینی و تحلیل روند مناسبتر است. بهترین کاربرد آن در زمینههای اقتصاد، مالی و بازارهای سهام است که در آن ارزش هر متغیر آتی با کمک متغیرهای موجود و رابطه بین آنها پیشبینی میشود.
- روش حداقل مربعات نزدیکترین رابطه را بین متغیرها فراهم می کند. تفاوت بین مجموع مربعات باقیمانده تا خط بهترین تناسب در این روش حداقل است.
- مکانیزم محاسباتی ساده و کاربردی است.
معایب
- روش حداقل مربعات بر ایجاد نزدیکترین رابطه بین مجموعه معینی از متغیرها متکی است. مکانیسم محاسباتی به دادهها حساس است و در صورت وجود هر گونه اطلاعات پرت (دادههای استثنایی)، نتایج ممکن است به طور عمده تأثیر بگذارند.
- این نوع محاسبه برای مدل های خطی مناسب است. برای معادلات غیر خطی، مکانیسم های محاسباتی جامع تری اعمال می شود.
نتیجه
روش حداقل مربعات یکی از متداول ترین روش های مورد استفاده برای مدل های پیش بینی وتحلیل روند. هنگامی که به درستی محاسبه شود، بهترین نتایج را ارائه می دهد.
منبع
https://www.wallstreetmojo.com/least-squares-regression/
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.