​

بیان مشکل [ ویرایش ]

هدف شامل تنظیم پارامترهای یک تابع مدل برای بهترین تناسب با یک مجموعه داده است. یک مجموعه داده ساده از n نقطه (جفت داده) تشکیل شده است.(x_{i},y_{i})\!, i = 1, …, n , جایی کهx_{i}\!یک متغیر مستقل است وy_{i}\!یک متغیر وابسته است که مقدار آن با مشاهده پیدا می شود. تابع مدل دارای فرم است{\displaystyle f(x,{\boldsymbol {\beta }})}، که در آن m پارامترهای قابل تنظیم در بردار نگهداری می شوند{\boldsymbol {\beta }}. هدف یافتن مقادیر پارامتر برای مدلی است که "بهترین" با داده ها مطابقت دارد. تناسب یک مدل با یک نقطه داده با باقیمانده آن اندازه گیری می شود که به عنوان تفاوت بین مقدار مشاهده شده متغیر وابسته و مقدار پیش بینی شده توسط مدل تعریف می شود:

{\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }}).}

باقی مانده ها در برابر متناظر رسم می شوندایکسارزش های. نوسانات تصادفی در مورد{\displaystyle r_{i}=0}نشان می دهد که یک مدل خطی مناسب است.

روش حداقل مربعات با به حداقل رساندن مجموع مجذور باقیمانده ، مقادیر پارامتر بهینه را پیدا می کند .اس: [10]

{\displaystyle S=\sum _{i=1}^{n}r_{i}^{2}.}

نمونه ای از یک مدل در دو بعدی مدل خط مستقیم است. نشان دادن قطع y به عنوان\بتا _{0}و شیب به عنوان\بتا _{1}، تابع مدل توسط داده می شودf(x,\boldsymbol \beta)=\beta_0+\beta_1 x. حداقل مربعات خطی را برای نمونه ای کامل از این مدل ببینید.

یک نقطه داده ممکن است از بیش از یک متغیر مستقل تشکیل شده باشد. به عنوان مثال، هنگامی که یک هواپیما را به مجموعه ای از اندازه گیری های ارتفاع برازش می دهیم، صفحه تابعی از دو متغیر مستقل x و z است. در کلی‌ترین حالت ممکن است یک یا چند متغیر مستقل و یک یا چند متغیر وابسته در هر نقطه داده وجود داشته باشد.

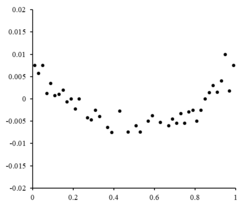
در سمت راست یک نمودار باقی مانده است که نوسانات تصادفی را نشان می دهد{\displaystyle r_{i}=0}، نشان می دهد که یک مدل خطی است{\displaystyle (Y_{i}=\alpha +\beta x_{i}+U_{i})}مناسب است.U_{i}یک متغیر مستقل و تصادفی است. [10]  

باقی مانده ها در برابر مربوطه رسم می شوندایکسارزش های. شکل سهمی از نوسانات در مورد{\displaystyle r_{i}=0}نشان می دهد که یک مدل سهموی مناسب است.

اگر نقاط باقیمانده دارای نوعی شکل بودند و به طور تصادفی در نوسان نبودند، یک مدل خطی مناسب نخواهد بود. به عنوان مثال، اگر نمودار باقیمانده یک شکل سهموی داشته باشد که در سمت راست دیده می شود، یک مدل سهموی{\displaystyle (Y_{i}=\alpha +\beta x_{i}+\gamma x_{i}^{2}+U_{i})}برای داده ها مناسب خواهد بود. باقی مانده برای یک مدل سهموی را می توان از طریق محاسبه کردta  {\displaystyle r_{i}=y_{i}-{\hat {\alpha }}-{\hat {\beta }}x_{i}-{\widehat {\gamma }}x_{i}^{2 }}. [10]

محدودیت ها [ ویرایش ]

این فرمول رگرسیون فقط خطاهای مشاهده‌ای را در متغیر وابسته در نظر می‌گیرد (اما رگرسیون مجموع حداقل مربعات جایگزین می‌تواند خطاها را در هر دو متغیر محاسبه کند). دو زمینه نسبتاً متفاوت با مفاهیم متفاوت وجود دارد:

  • رگرسیون برای پیش بینی در اینجا یک مدل برای ارائه یک قانون پیش‌بینی برای کاربرد در موقعیت مشابهی که داده‌های مورد استفاده برای برازش در آن اعمال می‌شود، برازش داده می‌شود. در اینجا، متغیرهای وابسته مربوط به چنین کاربردهای آتی، مشمول همان نوع خطای مشاهداتی هستند که در داده‌های مورد استفاده برای برازش استفاده می‌شوند. بنابراین منطقاً استفاده از قانون پیش‌بینی حداقل مربعات برای چنین داده‌هایی سازگار است.
  • رگرسیون برای تناسب یک "رابطه واقعی". در تجزیه و تحلیل رگرسیون استاندارد که منجر به برازش حداقل مربعات می شود، این فرض ضمنی وجود دارد که خطاهای متغیر مستقل صفر هستند یا به شدت کنترل می شوند تا ناچیز باشند. هنگامی که خطاهای متغیر مستقل غیر قابل چشم پوشی هستند، می توان از مدل های خطای اندازه گیری استفاده کرد. چنین روش هایی می تواند منجر به تخمین پارامترها ، آزمون فرضیه ها و فواصل اطمینان شود که وجود خطاهای مشاهده در متغیرهای مستقل را در نظر می گیرد. [11] یک رویکرد جایگزین، برازش یک مدل با حداقل مجذورات کل است; این را می توان به عنوان اتخاذ یک رویکرد عمل گرایانه برای متعادل کردن اثرات منابع مختلف خطا در فرمول بندی یک تابع هدف برای استفاده در برازش مدل در نظر گرفت.

حل مسئله حداقل مربعات [ ویرایش ]

حداقل مجموع مربع ها با صفر کردن گرادیان به دست می آید . از آنجایی که مدل دارای پارامترهای m است، معادلات شیب m وجود دارد:

 

{\displaystyle {\frac {\partial S}{\partial \beta _{j}}}=2\sum _{i}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}}=0،\ j=1،\ldots،m،}

و ازr_i=y_i-f(x_i،\boldsymbol \بتا)، معادلات گرادیان تبدیل می شود

 

{\displaystyle -2\sum _{i}r_{i}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}= 0،\ j=1،\ldots، m.}

 

معادلات گرادیان برای تمام مسایل حداقل مربعات اعمال می شود. هر مسئله خاص به عبارات خاصی برای مدل و مشتقات جزئی آن نیاز دارد. [12]

حداقل مربعات خطی [ ویرایش ]

مقاله اصلی: حداقل مربعات خطی

یک مدل رگرسیون زمانی خطی است که مدل ترکیبی خطی از پارامترها باشد، به عنوان مثال،

 

{\displaystyle f(x,{\boldsymbol {\beta }})=\sum _{j=1}^{m}\beta _{j}\phi _{j}(x)،}

که در آن تابع\phi _{j}تابعی ازایکس. [12]

 

اجازه دادن{\displaystyle X_{ij}=\phi _{j}(x_{i})}و قرار دادن متغیرهای مستقل و وابسته در ماتریسایکسوYبه ترتیب می توانیم حداقل مربعات را به صورت زیر محاسبه کنیم. توجه داشته باشید کهدیمجموعه ای از تمام داده ها است. [12] [13]

 

 

{\displaystyle L(D,{\boldsymbol {\beta }})=\left\|YX{\boldsymbol {\beta }}\right\|^{2}=(YX{\boldsymbol {\beta }}) ^{\mathsf {T}}(YX{\boldsymbol {\beta }})=Y^{\mathsf {T}}YY^{\mathsf {T}}X{\boldsymbol {\beta }}-{\ علامت برجسته {\beta }}^{\mathsf {T}}X^{\mathsf {T}}Y+{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}X {\boldsymbol {\beta }}}

 

یافتن حداقل را می توان از طریق صفر کردن گرادیان ضرر و حل آن به دست آورد{\boldsymbol {\beta }}

 

{\displaystyle {\frac {\partial L(D,{\boldsymbol {\beta }})}{\partial {\boldsymbol {\beta }}}}={\frac {\partial \left(Y^{\ mathsf {T}}YY^{\mathsf {T}}X{\boldsymbol {\beta }}-{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}Y+ {\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}X{\boldsymbol {\beta }}\right)}{\partial {\boldsymbol {\beta }}} }=-2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}}

 

در نهایت گرادیان از دست دادن را بر روی صفر قرار داده و برای را حل کنید{\boldsymbol {\beta }}دریافت می کنیم: [13] [12]

 

{\displaystyle -2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}=0\Rightarrow X^{\mathsf {T}}Y=X^ {\mathsf {T}}X{\boldsymbol {\beta }}}

 

{\displaystyle {\boldsymbol {\hat {\beta }}}=\left(X^{\mathsf {T}}X\right)^{-1}X^{\mathsf {T}}Y}

 

حداقل مربعات غیر خطی [ ویرایش ]

مقاله اصلی: حداقل مربعات غیر خطی

در برخی موارد، یک راه حل با شکل بسته برای مسئله حداقل مربعات غیرخطی وجود دارد - اما به طور کلی وجود ندارد. در صورت عدم پاسخ به شکل بسته، از الگوریتم های عددی برای یافتن مقدار پارامترها استفاده می شود.{\displaystyle \بتا }\بتاکه هدف را به حداقل می رساند. اکثر الگوریتم ها شامل انتخاب مقادیر اولیه برای پارامترها هستند. سپس، پارامترها به صورت مکرر پالایش می شوند، یعنی مقادیر با تقریب متوالی به دست می آیند:

 

{\displaystyle {\beta _{j}}^{k+1}={\beta _{j}}^{k}+\Delta \beta _{j}،}

که در آن بالانویس k یک عدد تکرار و بردار افزایش ها است\دلتا \بتا _{j}بردار شیفت نامیده می شود. در برخی از الگوریتم‌های متداول، در هر تکرار ممکن است مدل با تقریب به یک بسط سری تیلور مرتبه اول خطی شود.{\boldsymbol \beta }^{k}:

 

{\displaystyle {\begin{aligned}f(x_{i},{\boldsymbol {\beta }})&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}\left(\beta _{j}-{\ بتا _{j}}^{k}\right)\\&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}J_{ij}\, \Delta \بتا _{j}.\end{تراز شده}}}

 

J Jacobian تابعی از ثابت ها، متغیر مستقل و پارامترها است، بنابراین از یک تکرار به تکرار دیگر تغییر می کند. باقی مانده توسط داده شده است

 

{\displaystyle r_{i}=y_{i}-f^{k}(x_{i},{\boldsymbol {\beta }})-\sum _{k=1}^{m}J_{ik} \,\Delta \beta _{k}=\Delta y_{i}-\sum _{j=1}^{m}J_{ij}\,\Delta \beta _{j}.}

 

برای به حداقل رساندن مجموع مربع هایr_{i}، معادله گرادیان صفر تنظیم شده و برای آن حل می شود\دلتا \بتا _{j}:

 

{\displaystyle -2\sum _{i=1}^{n}J_{ij}\left(\Delta y_{i}-\sum _{k=1}^{m}J_{ik}\,\ دلتا \بتا _{k}\right)=0,}

که در بازآرایی تبدیل به m معادلات خطی همزمان می شوند، معادلات عادی :

 

{\displaystyle \sum _{i=1}^{n}\sum _{k=1}^{m}J_{ij}J_{ik}\,\Delta \beta _{k}=\sum _{ i=1}^{n}J_{ij}\,\Delta y_{i}\qquad (j=1,\ldots ,m).}

 

معادلات عادی به صورت نماد ماتریسی نوشته می شوند

 

{\displaystyle \left(\mathbf {J} ^{\mathsf {T}}\mathbf {J} \right)\Delta {\boldsymbol {\beta }}=\mathbf {J} ^{\mathsf {T} }\Delta \mathbf {y}.}

 

اینها معادلات تعیین کننده الگوریتم گاوس-نیوتن هستند.

تفاوت بین حداقل مربعات خطی و غیرخطی [ ویرایش ]

  • تابع مدل، f ، در LLSQ (حداقل مربعات خطی) ترکیبی خطی از پارامترهای فرم است.f = X_{i1}\beta_1 + X_{i2}\beta_2 +\cdotsاین مدل ممکن است یک خط مستقیم، یک سهمی یا هر ترکیب خطی دیگری از توابع را نشان دهد. در NLLSQ (حداقل مربعات غیرخطی) پارامترها به عنوان توابع ظاهر می شوند، مانند\beta^2، e^{\بتا x}و غیره اگر مشتقات{\displaystyle \partial f/\partial \beta _{j}}یا ثابت هستند یا فقط به مقادیر متغیر مستقل بستگی دارند، مدل در پارامترها خطی است. در غیر این صورت مدل غیر خطی است.
  • برای یافتن راه حل برای یک مشکل NLLSQ به مقادیر اولیه برای پارامترها نیاز دارید. LLSQ به آنها نیاز ندارد.
  • الگوریتم های حل برای NLLSQ اغلب نیاز دارند که Jacobian را بتوان مشابه LLSQ محاسبه کرد. عبارات تحلیلی برای مشتقات جزئی می تواند پیچیده باشد. اگر عبارات تحلیلی به دست آوردن غیرممکن باشد، باید مشتقات جزئی را با تقریب عددی محاسبه کرد یا باید تخمینی از ژاکوبین انجام داد، اغلب از طریق تفاوت های محدود .
  • عدم همگرایی (شکست الگوریتم در یافتن حداقل) یک پدیده رایج در NLLSQ است.
  • LLSQ در سطح جهانی مقعر است، بنابراین عدم همگرایی مشکلی نیست.
  • حل NLLSQ معمولاً یک فرآیند تکراری است که باید با برآورده شدن یک معیار همگرایی خاتمه یابد. راه‌حل‌های LLSQ را می‌توان با استفاده از روش‌های مستقیم محاسبه کرد، اگرچه مسائل با تعداد زیادی پارامتر معمولاً با روش‌های تکراری حل می‌شوند، مانند روش گاوس – سیدل .
  • در LLSQ راه حل منحصر به فرد است، اما در NLLSQ ممکن است چندین حداقل در مجموع مربع ها وجود داشته باشد.
  • تحت شرایطی که خطاها با متغیرهای پیش‌بینی‌کننده همبستگی ندارند، LLSQ تخمین‌های بی‌طرفانه به دست می‌دهد، اما حتی تحت آن شرایط، تخمین‌های NLLSQ عموماً بایاس هستند.

هر زمان که به دنبال راه حل برای یک مسئله حداقل مربعات غیرخطی هستیم، این تفاوت ها باید در نظر گرفته شوند. [12]

منبع

https://en.wikipedia.org/wiki/Least_squares

​