ادامه فضای بردار توپولوژیکی

توسط علی رضا نقش نیلچی | سه شنبه سی و یکم تیر ۱۳۹۹ | 15:5

انواع [ ویرایش ]

بسته به نوع برنامه ، محدودیت های اضافی معمولاً در ساختار توپولوژیکی فضا اعمال می شود. در حقیقت ، چندین نتیجه اصلی در تحلیل عملکردی به طور کلی برای فضاهای بردار توپولوژیکی در نظر نمی گیرند: قضیه نمودار بسته ، قضیه نقشه برداری باز و این واقعیت که فضای دوگانه فضا نقاطی را در فضا جدا می کند.

در زیر برخی از فضاهای مشترک بردار topological، یعنی در حدود خود دستور داده است خوب بودن .

فضای اف هستند کامل فضاهای برداری توپولوژیک با متریک ترجمه ثابت. این خدمات عبارتند از L p فضاهای برای همه P> 0 .
فضاهای بردار توپولوژیکی محدب محلی : در اینجا هر نقطه دارای یک پایگاه محلی است که از مجموعه های محدب تشکیل شده است . با تکنیکی که به عنوان عملکردهای مینکوفسکی شناخته می شود ، می توان نشان داد که فضایی به صورت محلی محدب است ، اگر و تنها در صورت تعریف توپولوژی آن توسط خانواده ای از هنجارهای نیمه تعریف شود. محدب محلی حداقل نیاز برای استدلالهای "هندسی" مانند قضیه هان-باناخ است . L p فضاها به صورت محلی محدب (در واقع، فضای باناخ) برای همه ص ≥ 1 ، اما نه برای 0 < P <1 .
فضاهای باریک : فضاهای محدب محلی که قضیه Banach-Steinhaus در آن نگهداری می شود.
فضای بورنولوژیکی : یک فضای محدب محلی که در آن عملگرهای خطی مداوم به هر فضای محدب محلی دقیقاً عملگرهای خطی محدود هستند .
فضای کلیشه ای : یک فضای محدب محلی که یک نوع شرایط انعطاف پذیری را برآورده می کند ، جایی که فضای دوگانه با توپولوژی همگرایی یکنواخت در مجموعه هایی کاملاً محدود وجود دارد .
فضای MONTEL : یک فضای که در آن هر بشکه بسته و مجموعه کراندار است جمع و جور
فضاهای Fréchet : اینها فضاهای کاملاً محدب محلی هستند که توپولوژی از یک معیار ترجمه متغیر یا معادل آن ناشی می شود: از یک خانواده قابل شمارش از هنجارهای نیمه. بسیاری از فضاهای جالب توابع در این کلاس قرار می گیرند. یک فضای F محدب محلی به صورت محلی فضایی Fréchet است.
LF-فضاهای هستند محدودیت از فضاهای فریشه . فضاهای ILH هستند محدودیت معکوس فضای هیلبرت.
فضاهای هسته ای : اینها فضاهای محدب محلی هستند با این خاصیت که هر نقشه محدودی از فضای هسته ای گرفته تا فضای دلخواه باناک یک عامل هسته ای است .
فضاهای نرمال و فضاهای نیمه هنجار : فضاهای محدب محلی که در آن می توان توپولوژی را با یک هنجار منفرد یا نیمه هنجار توصیف کرد . در فضاهای دارای هنجار ، یک عملگر خطی در صورت محدود بودن و در صورت محدود بودن ، مداوم است.
فضاهای بانواچ : فضاهای بردار کامل شده را تکمیل کنید . بیشتر تجزیه و تحلیل عملکردی برای فضاهای Banach تدوین شده است.
فضاهای انعکاس پذیر Banach : فضاهای Banach به طور طبیعی از دوتایی آنها (مانند تصویر زیر) همخوان است ، که تضمین می کند برخی از استدلال های هندسی قابل انجام باشند. یک مثال مهم است که نه انعکاسی است L 1 ، که دوگانه است L ∞ اما به شدت در دوگانه موجود L ∞ .
فضاهای هیلبرت : اینها یک محصول داخلی دارند . حتی اگر این فضاها ممکن است نامتناهی باشد ، بیشتر استدلال هندسی آشنا از ابعاد محدود می تواند در آنها انجام شود. اینها شامل فضاهای L 2 است.
فضاهای اقلیدسی : ℝ n یا ℂ n با توپولوژی ناشی از محصول داخلی استاندارد. همانطور که در بخش قبل اشاره شد ، برای یک n محدود محدود ، فقط یک فضای بردار توپولوژیکی n بعدی ، تا ایزومورفیسم وجود دارد. از این مسئله نتیجه می گیرد که هر فضای فرعی بعدی یک TVS بسته است. مشخصه ای از ابعاد محدود این است که یک تلویزیون Haus Hausff اگر و فقط در صورت محدود بودن ابعاد محدود باشد ، بصورت محلی فشرده است (بنابراین برای برخی از فضای اقلیدسی ایزومورفیک است).

فضای دوگانه [ ویرایش ]

هر فضای برداری توپولوژیکی است فضای پیوسته دو یعنی مجموعه ای X * از همه توابع خطی پیوسته، یعنی خطی پیوسته نقشه از فضای را در زمینه پایه 𝕂 . توپولوژی روی دوتایی می تواند به عنوان درشت ترین توپولوژی تعریف شود به گونه ای که جفت شدن هر یک از ارزیابی نقطه X * → continuous پیوسته است. این دوتایی را به یک فضای بردار توپولوژیکی محدب محلی تبدیل می کند. این توپولوژی توپولوژی ضعیف نامیده می شود . این ممکن است تنها توپولوژی طبیعی در فضای دوگانه باشد. به عنوان مثال ، فضای دوگانه طبیعی دارای یک هنجار طبیعی است که بر روی آن تعریف شده است. با این حال ، این به دلیل خاصیت فشردگی در کاربردها بسیار مهم استقضیه Banach – Alaoglu ). احتیاط: هرگاه X یک فضای محدب غیرقابل تنظیم باشد ، نقشه جفت شدن X * × X → continuous هرگز پیوسته نیست ، مهم نیست که توپولوژی فضای برداری کدام یک را در V * انتخاب کند .

خواص [ ویرایش ]

همچنین ببینید: فضای بردار توپولوژیکی محدب محلی به صورت محلی محدب

بگذارید X یک TVS باشد (لزوماً Hausdorff یا محلی محدب نیست). هر TVS یک گروه توپولوژیکی قابل تعویض است (علاوه بر این و نفی به عنوان عملیات گروهی).

تعریف : برای هر گونه S ⊆ X از محدب (. RESP و متعادل کننده شده ، disked ، محدب بسته، متعادل کننده بسته، disked بسته ) بدنه از S کوچکترین زیر مجموعه از است X است که این اموال و شامل S .

ما بسته (داخلی داخلی ، بدنه محدب ، بدنه متعادل ، بدنه دیسک را نشان می دهیم) مجموعه S توسط cl S (به ترتیب Int S ، co S ، bal S ، cobal S ) نشان می دهیم.

ترجمه توپولوژی ثابت

یكی از بیشترین خصوصیات توپولوژی برداری این است كه هر توپولوژی برداری به صورت ثابت ترجمه می شود:

برای همه X 0 ∈ X ، نقشه X → X تعریف شده توسط X ↦ X 0 + X است همسانریختی .

بنابراین برای هر x ∈ X و هر زیر مجموعه S ⊆ X ، x + S یک محله (توپولوژی) محله (محله باز ، محله بسته) از x است و اگر فقط در S اصل هم صادق است.

نقشه X → X تعریف شده توسط x ↦ - x نیز یک هومومورفیسم است.

خواص محلات و مجموعه های باز

زیرمجازهای محدب باز یک TVS X (لزوماً Hausdorff یا محدب محلی نیستند) دقیقاً مواردی هستند که از فرم z + { x ∈ X هستند : p ( x ) <1} = { x ∈ X : p ( x - z ) <1 } برای برخی از Z ∈ X و برخی مداوم مثبت زیر خطدار کاربردی ص در X . [9]
اگر S ⊆ X و U زیر مجموعه باز X باشد ، S + U یک مجموعه باز در X است . [1]
هر محله 0 یک مجموعه جاذبه است و حاوی محله ای متعادل با 0. است. [1]
مبدأ دارای یک محله محله است که از محله های متعادل بسته از 0 تشکیل شده است. اگر فضا به صورت محلی محدب باشد ، آنگاه دارای محله ای همسایه از محله های متعادل محدب محدب بسته از 0 است.
اگر S ⊆ X دارای فضای داخلی خالی باشد ، S - S محله ای با 0 است. [1]
اگر K یک IS جذب دیسک در یک TVS X و اگر P : = P K است مینکوفسکی کاربردی از K پس از آن [10]
Int K ⊆ { x ∈ X : p ( x ) <1} ⊆ K ⊆ { x ∈ X : p ( x ) 1} ⊆ Cl K
- توجه داشته باشید که ما تصور نمی کردیم که K خاصیت توپولوژیکی داشته باشد و آن p هم پیوسته باشد (که اگر و فقط اگر K محله 0 باشد ، اتفاق می افتد ).
دیسک در یک TVS است هیچ جا چگال اگر و تنها اگر بسته شدن آن یک محله از مبدا است. [11]
هر زیر مجموعه باز متصل به یک TVS به صورت قوس متصل است .
اجازه دهید τ و υ شود دو توپولوژی برداری روی X . سپس τ ⊆ υ اگر و تنها اگر هر زمان که یک شبکه X • = ( X من ) من ∈ من در X همگرا 0 در ( X ، υ) سپس X • → 0 در ( X ، τ) . [12]
بگذارید مبدأ محله ای در مبدا X باشد ، بگذارید S ⊆ X و اجازه دهید x ∈ X باشد. سپس X ∈ CL S اگر و تنها اگر یک شبکه وجود دارد بازدید کنندگان • = ( بازدید کنندگان N ) N ∈ 𝒩 در S (نمایه شده توسط 𝒩 ) به صورتی که بازدید کنندگان • → X در X . [13]
- به ویژه ، این امر نشان می دهد كه غالباً در نظر گرفتن مشكلات شبكه ای كه مبنای همسایگی آنها از مبدأ قرار دارند ، كافی است تا شبكه هایی در مجموعه های كارگردانی دلخواه.

داخلی

اگر S دارای فضای داخلی خالی باشد ، Int S = Int (cl S ) و cl S = cl (Int S ) .
اگر R ، S ⊆ X و S دارای فضای داخلی خالی باشد ، Int ( R ) + Int ( S ) R + Int ( S ) ⊆ Int ( R + S ) .
اگر S یک دیسک در X باشد که داخلی خالی ندارد ، 0 متعلق به فضای داخلی S است . [14]
- با این حال ، یک زیر مجموعه بسته متعادل از X با فضای داخلی خالی ممکن است در فضای داخلی خود 0 باشد. [14]
اگر S یک متعادل زیر مجموعه ای از X که داخلی شامل منشاء سپس المللی S و متعادل کننده شده است. [1] اگر فضای داخلی یک مجموعه متعادل خالی باشد اما منشأ آن را شامل نشود (چنین مجموعه هایی حتی در 2 پوند نیز وجود دارد ) ، بنابراین آن داخلی نمی تواند یک مجموعه متعادل باشد.
اگر X متعلق به داخلی S ⊆ X و Y ∈ CL S ، پس از آن نیمه باز خط بخش [ X ، Y ): = { TX + (1 - تی ) Y : 0 < تی ≤ 1} ⊆ بین المللی S .

کامل بودن

هر TVS دارای تکمیل است و هر تلویزیون تلویزیونی Hausdorff دارای تکمیل Hausdorff است. [1]
یک زیر مجموعه کامپکت از TVS (لزوماً Hausdorff) کامل نیست. [15]
اگر یک TVS دارای یک محله کامل از مبدا باشد ، کامل است. [15]
یک زیر مجموعه کامل از تلویزیون Haus Hausff بسته است. [15]
اگر C یک زیر مجموعه کامل از TVS باشد ، هر زیر مجموعه ای از C که در C بسته است کامل است. [15]

مجموعه بسته و بسته

اگر S ⊆ X و a یک مقیاس باشد ، یک cl ( S ) ⊆ Cl ( aS ) ؛ اگر X هاسدورف، است ≠ 0 ، یا S = ∅ سپس برابری نگه می دارد: CL ( به عنوان ) = CL ( S ) .
- بنابراین ، هر مضرب مقیاس غیر صفر یک مجموعه بسته بسته است. اگر X از Hausdorff باشد ، هر مكثر مقياس يك مجموعه بسته بسته مي شود.
اگر S ⊆ X و S + S ⊆ 2 cl S باشد ، Cl S محدب است. [16]
اگر R ، S ⊆ X سپس cl ( R ) + cl ( S ) ⊆ cl ( R + S ) و cl [cl ( R ) + cl ( S )] = cl ( R + S ) . [1] بنابراین اگر R + S بسته باشد ، Cl ( R ) + Cl ( S ) نیز هست . [16]
اگر S ⊆ X و x ∈ X ، cl ( x + S ) = x + cl ( S ) . [1]
اگر S ⊆ X و اگر R مجموعه ای از مقیاس ها باشد به گونه ای که نه cl S و نه cl R حاوی صفر نیست (cl R ) (cl S ) = cl ( RS ) . [16]
بستن یک فضای بردار یک TVS یک فضای بردار است (بنابراین به طور خاص ، بسته شدن {0 } یک فضای فرعی بردار است).
اگر S ⊆ X سپس cl S =∩N ∈ 𝒩( S + N ) که در آن 𝒩 هر پایه محله در حالت های است X . [17]
- به طور خاص ، هر محله مبدا بسته به {0 است .
- از این رو نتیجه می گیرد که هر زیر مجموعه S از cl ({0}) که حاوی منشا باشد کاملاً جمع و جور است و بنابراین کامل است (برای اثبات به پاورقی مراجعه کنید) [18] . به طور خاص ، اگر X هاوسدورف نباشد ، مجموعه های کاملاً جمع و جور و بسته ای وجود دارند که بسته نیستند.
- توجه داشته باشید که مجموعه های S در TVS X به گونه ای هستند که cl S ≠ ∩ { U : S ⊆ U ، U در X } باز شود . [19]
اگر X یک TVS واقعی و S ⊆ X است ، پس از آن∩r > 1 rS ⊆ cl S ؛ اگر S محله محدب از مبدأ باشد ، برابری در آن وجود دارد.
مجموعه یک مجموعه جمع و جور و یک مجموعه بسته بسته است. با این حال ، ممکن است جمع دو زیرمجموعه بسته نتواند بسته شود. [1]
اگر M یک فضای بردار X و N باشد یک محله بسته از 0 در X است به طوری که U ∩ N در X بسته می شود ، سپس M در X بسته می شود . [20]
یک فضای بردار بردار توپولوژیکی کامل از یک Haussffff TVS بسته است. [1]
هر فضای فرعی بردار ابعادی متناسب با یک TVS Hausdorff بسته است. مجموع یک فضای فرعی بردار بسته و یک فضای فرعی وکتور محدود بعدی بسته است. [1]
فضای فرعی و بردار TVS که بسته است اما باز نیست ، هیچ جا متراکم نیست . [11]

تپه های بسته

بدنه محدب بسته یک مجموعه برابر با بسته شدن پوسته محدب آن مجموعه است (یعنی به cl (co ( S )) ). [1]
تعادل بسته بسته یک مجموعه برابر با بسته شدن پوسته متعادل آن مجموعه است (یعنی به cl (bal ( S )) ). [1]
پوسته بسته دیسک بسته با بسته شدن دیسک دیسک آن مجموعه برابر است (یعنی به cl (cobal ( S )) ). [1]
اگر R ، S ⊆ X و پوسته محدب بسته یکی از مجموعه S یا R جمع و جور باشد ، Cl (co ( R )) + cl (co ( S )) = cl (co ( R + S )) . [1]
اگر R ، S ⊆ X هرکدام یک پوسته محدب بسته داشته باشد که جمع و جور باشد ( یعنی cl (co ( R )) و cl (co ( S )) جمع و جور هستند)) سپس cl (co ( R ∪ S )) = co [cl ( co ( R )) ∪ cl (co ( S ))] .

مجموعه های کامپکت و کاملاً محدود

زیر مجموعه یک TVS اگر کاملاً کامل و کاملاً محدود باشد کاملاً فشرده است. [21]
- بنابراین ، در یک TVS کامل ، یک زیر مجموعه بسته و کاملاً محدود جمع و جور است. [21]
در هر TVS غیر Hausdorff یک مجموعه جمع و جور (و در نتیجه کامل) وجود دارد که بسته نیست (برای مثال به پاورقی مراجعه کنید). [22] [21]
بسته شدن یک مجموعه کاملاً محدود.
هر مجموعه کاملاً محدود کاملاً محدود. [21]
هر مجموعه نسبتاً جمع و جور کاملاً محدود است. [21]
تصویر یک مجموعه کاملاً محدود تحت یک نقشه یکنواخت مداوم (به عنوان مثال یک نقشه خطی مداوم) کاملاً محدود است. [21]
در یک فضای محدب محلی ، هر ترکیب خطی از مجموعه های کاملاً محدود کاملاً محدود است. [23]
اگر K یک زیر مجموعه جمع و جور از TVS است X و U یک زیر مجموعه باز است X containg K ، پس از آن وجود دارد یک محله وجود دارد N از 0 به طوری که K + N ⊆ U . [20]

قلاب و فشردگی

در یک TVS عمومی ، پوسته محدب بسته یک مجموعه جمع و جور ممکن است نتواند فشرده باشد.

بدنه متعادل یک مجموعه کامپکت ( کاملاً محدود ) دارای همین خاصیت است. [1]
در یک فضای Frecchet ، پوسته محدب بسته یک مجموعه جمع و جور جمع و جور است. [24]
بدنه محدب از یک اتحادیه محدود از مجموعه های محدب جمع و جور دوباره جمع و جور و محدب است. [1]
در یک فضای محدب محلی ، بدنه محدب و پوسته دیسک شده از یک مجموعه کاملاً محدود محدود است. [1]
در یک فضای کامل محدب محلی ، بدنه محدب و پوسته دیسک دیسک یک مجموعه جمع و جور هر دو جمع و جور هستند. [1]
- به طور کلی، اگر K یک زیر مجموعه جمع و جور از فضا در سطح محلی محدب است، پس از آن محدب شرکت K (محدوده بدنه disked cobal K ) جمع و جور است اگر و تنها اگر آن را کامل است. [1]

محدودیت

هر مجموعه کاملاً محدود محدود است. [23]
یک مجموعه محدود است اگر و فقط اگر هر یک از پیامدهای آن مجموعه ای محدود است. [23]
یک فضای بردار یک TVS محدود است اگر و فقط در صورتی که در بسته شدن } 0 contained موجود باشد. [23]
در یک فضای محدب محلی ، پوسته های محدب از مجموعه های محدود شده محدود شده اند. این به طور کلی برای TVS صحیح نیست. [23]
اگر M یک زیرفضای برداری از TVS است X ، پس از آن یک زیر مجموعه از M در محدود M اگر و تنها اگر آن را در محدود X . [23]

سری و دنباله ها

یک سری Σ∞
من = 1 X من شده است که گفت همگرایی در یک TVS X اگر دنباله مجموع همگرا با مشتقات جزئی.
اگر یک سری Σ∞
من = 1 X من همگرا در یک TVS X پس از آن ایکس من → 0 در X . [25]

حقایق مهم جبری و تصورات غلط رایج

اگر S ⊆ X سپس 2 S ⊆ S + S ؛ اگر S محدب باشد ، برابری وجود دارد.
- برای مثال که در آن برابری کند نیست را نگه دارید، اجازه دهید X غیر صفر و مجموعه S = {- X ، X }؛ S = { x ، 2 x } نیز کار می کند.
زیر مجموعه C محدب است اگر و تنها اگر ( بازدید کنندگان + تی ) C = SC + TC برای همه واقعی مثبت ها و تی . [26]
بدنه دیسک شده از مجموعه S ⊆ X برابر است با محدب محدب از بدنه متعادل S (یعنی به همکاری (بال ( S )) ).
- با این حال ، به طور کلی شرکت (bal ( S )) ≠ bal (co ( S )) .
زیر مجموعه متعادل S است جذب اگر و تنها اگر برای هر x را ∈ X وجود دارد، برخی از اسکالر وجود دارد به طوری که تبر ∈ S . [1]
اگر R ، S ⊆ X و یک اسکالر است و سپس شرکت ( R + S ) = شرکت R + CO S و CO ( به عنوان ) = شرکت S . [1]
اگر R ، S ⊆ X مجموعه های جدا کننده غیر خالی محدب و x ∉ R ∪ S باشند ، پس S ∩ co ( R ∪ { x }) = ∅ یا R ∩ ( S ∪ { x }) = .
در هر فضای بردار غیر بدیهی X ، دو زیر مجموعه محدب غیر خالی وجود دارد که اتحاد X است .

خواص دیگر

هر TVS کاملاً منظم است . با این وجود ، یک TVS نباید طبیعی باشد. [27]
هر TVS متصل است . [1]
یک تلویزیون است pseudometrizable اگر و تنها اگر آن را به یک پایه و اساس محله شمارا در مبدا، یا معادل آن، اگر و تنها اگر توپولوژی آن است که توسط یک تولید F -seminorm . TVS قابل اندازه گیری است اگر و فقط اگر Hausdorff و قابل اندازه گیری است.
هر توپولوژی TVS توسط خانواده ای از F- seminorms ایجاد می شود. [28]
فرض کنید X یک TVS است که دارای توپولوژی نامشخص است . سپس X یک فضای Baire است اگر و فقط اگر X هیچ زیر مجموعه ای متراکم و جاذبه در هیچ جا جذب نکرده باشد. [11]
TVS X یک فضای Baire است اگر و فقط اگر X غیر مستهجن است ، اتفاق می افتد اگر و فقط اگر یک مجموعه D و D هیچ جایی متراکم وجود ندارد به گونه ای باشد که X =∪n ∈ ND . [11]
- توجه داشته باشید که هر تلویزیون غیر منتظره محلی محدب یک فضای خنجر است . [11]

خواص حفظ شده توسط اپراتورهای تنظیم شده [ ویرایش ]

بدنه متعادل یک مجموعه کامپکت ( کاملاً محدود ، باز) دارای همین خاصیت است. [1]
فضای داخلی یک مجموعه محدب محدب است. [1]
بسته شدن یک محدب (متناسب ، متعادل ، محدود ، جذب) همان ویژگی را دارد. [1]
بسته شدن یک فضای فرعی بردار یک فضای فرعی بردار است. [1]
مجموعه (مینکوفسکی) از دو مجموعه جمع و جور (به ترتیب محدود ، متعادل ، محدب) دارای همان خاصیت است. [1]
- جمع دو مجموعه بسته لازم نیست بسته شود.
مبالغ محدود ، اتحادیه های محدود ، مضرب های مقیاس پذیر ، زیرمجموعه ها ، درهای بسته ، فضای داخلی ، بدنه متعادل مجموعه های محدود. [23]
هر مضرب مقیاس مجموعه ای از محدب (نسبتاً متعادل) همان خاصیت را دارد.
هر مضرب مقیاس غیر صفر یک مجموعه باز (به عنوان مثال یک محله 0 ، یک مجموعه جاذب) یک مجموعه باز است (به عنوان مثال یک محله 0 ، یک مجموعه جاذب).
بدنه محدب از یک مجموعه متعادل (باز (باز)) متعادل است (به ترتیب باز).
- پوسته محدب یک مجموعه بسته نباید بسته شود. [1]
- بدنه محدب یک مجموعه محدود لازم نیست .

در جدول زیر ، رنگ هر سلول نشان می دهد که آیا خاصیت خاصی از زیر مجموعه های X (که با نام ستون به عنوان مثال "محدب نشان داده شده است) در زیر عملگر تنظیم شده است (نشان داده شده با نام ردیف به عنوان مثال" بسته شدن ") وجود دارد. اگر در هر TVS ، یک ویژگی تحت عملگر تعیین شده حفظ شود ، آن سلول به رنگ سبز رنگ خواهد بود. در غیر این صورت ، قرمز رنگ خواهد بود.

به عنوان مثال ، از آنجا که اتحاد دو مجموعه جذب کننده دوباره جذب می شود ، سلول در ردیف " R ∪ S " و ستون "جذب" به رنگ سبز رنگ می شوند. اما از آنجا که تقاطع دلخواه مجموعه های جذب کننده نیاز به جذب ندارد ، سلول در ردیف "تقاطع های دلخواه (حداقل 1 مجموعه)" و ستون "جذب" به رنگ قرمز رنگ است. اگر سلول رنگی نباشد ، آن اطلاعات هنوز پر نشده است.

منبع

https://en.wikipedia.org/wiki/Topological_vector_space

ادامه فضای بردار توپولوژیکی

توسط علی رضا نقش نیلچی | سه شنبه سی و یکم تیر ۱۳۹۹ | 14:40

توپولوژی بردار نهایی [ ویرایش ]

بگذارید X یک فضای برداری واقعی یا پیچیده باشد. وجود دارد یک TVS topololgy وجود دارد τ F در X است که بهتر از هر دیگر TVS-توپولوژی در X (این است که، هر TVS-توپولوژی در X لزوما یک زیر مجموعه از τ F ). [2] هر نقشه خطی از ( X ، 𝜏 f ) به TVS دیگر لزوماً مداوم است. [2] اگر X دارای یک غیر قابل شمارش اساس Hamel سپس τ F است نه به صورت محلی محدب و نه ناتهی یک مجموعه میگر .[2]

فضاهای بردار ضرب [ ویرایش ]

یک محصول دکارتی از خانواده ای از فضاهای بردار توپولوژیکی ، که وقف توپولوژی محصول باشد ، یک فضای بردار توپولوژیکی است. به عنوان مثال، مجموعه X از تمام توابع F : ℝ → ℝ : این مجموعه X را می توان با فضای شناسایی ℝ ℝ و حمل یک طبیعی توپولوژی کالا . با استفاده از این توپولوژی ، X به یک وکتور توپولوژیکی تبدیل می شود ، که دارای توپولوژی به نام توپولوژی همگرایی نقطه ای است . دلیل این نام به شرح زیر است: اگر ( f n ) دنباله ای از عناصر در X باشد، پس از آن F N است حد F ∈ X اگر و تنها اگر( F N ( X دارای محدودیت( F ( X برای هر عدد حقیقی x را . این فضای کامل است، اما normable است: در واقع، هر محله از 0 در توپولوژی محصول شامل خطوط، یعنی ، مجموعه 𝕂 F برای F ≠ 0 .

ساختار توپولوژیکی [ ویرایش ]

فضای برداری یک گروه آبلیان با توجه به عملکرد علاوه بر این است ، و در یک فضای بردار توپولوژیکی عملکرد معکوس همیشه مداوم است (از آنجا که همان ضرب با − 1 است). از این رو ، هر فضای بردار توپولوژیکی یک گروه توپولوژیکی بیلی است .

بگذارید X یک فضای بردار توپولوژیکی باشد. با توجه به فضای زیر M ⊂ X ، فضای کمّی X / M با توپولوژی بزرگ معمول یک فضای بردار توپولوژیکی Hausdorff است اگر و فقط در صورت بسته بودن M باشد. [3] این اجازه به ساخت زیر می دهد: با توجه به فضای بردار توپولوژیکی X (که احتمالاً Hausdorff نیست) ، فضای سهم X / M را تشکیل دهید که در آن M بسته شدن 0 {است. X / M سپس فضایی بردار توپولوژیکی Hausdorff است که می تواند به جای X مورد مطالعه قرار گیرد.

به طور خاص ، فضاهای بردار توپولوژیک فضاهای یکنواخت هستند و بنابراین می توان در مورد کامل بودن ، همگرایی یکنواخت و استمرار یکنواخت صحبت کرد . (این بدان معنی است که هر فضای بردار توپولوژیکی Hausdorff Tychonoff است . [4] ) فعالیت فضای بردار علاوه بر این به طور یکنواخت و مداوم است و ضرب مقیاس کوشکی مداوم است (با این حال ، تقریباً هرگز به طور یکنواخت مداوم نیست). به همین دلیل ، هر فضای بردار توپولوژیکی می تواند تکمیل شود و به این ترتیب یک فضای فرعی خطی متراکم از یک فضای بردار توپولوژیک کامل است.

قضیه Birkhoff-Kakutani به می دهد که سه شرط زیر در بردار topological فضای X معادل: [5]

مبدأ 0 در X بسته شده است ، و تعداد محله های قابل توجهی برای 0 در X وجود دارد .
X است ناتهی یک مجموعه میگر (به عنوان یک فضای توپولوژیک).
یک معیار ترجمه-متغیر در X وجود دارد که نشانگر توپولوژی داده شده در X است .

فضای خطی متریک معنی یک فضای برداری (حقیقی یا مختلط) همراه با یک متریک که جمع و ضرب اسکالر به طور مداوم می باشد. با قضیه بیرخوف-کاکوتی ، نتیجه می گیرد که یک معیار معادل وجود دارد که ترجمه-متغیر است.

با قوت بیشتر: فضای بردار توپولوژیکی گفته می شود که در صورت القاء توپولوژی آن ممکن است نرمال باشد. یک فضای بردار توپولوژیکی در صورتی که هاسدورف باشد و دارای محله ای محدب محدب باشد ، عادی است اگر و فقط قابل استفاده باشد. [6]

یک عملگر خطی بین دو فضای بردار توپولوژیکی که در یک نقطه مداوم است بر روی کل دامنه مداوم است. علاوه بر این، یک عملگر خطی F مداوم است اگر F ( X ) محدود است (به شرح زیر تعریف شده است) برای برخی از محله X 0.

یک ابرقابل هواپیما در یک وکتور توپولوژیکی فضای X یا متراکم یا بسته است. کاربردی خطی F در یک فضای برداری توپولوژیکی X است یا متراکم و یا هسته بسته شده است. علاوه بر این ، f در صورت بسته بودن هسته هسته ، پیوسته است .

اجازه دهید 𝕂 یک غیر گسسته موضعا فشرده درست توپولوژیک، برای مثال اعداد حقیقی یا اعداد مختلط. یک فضای برداری توپولوژیکی بیش از 𝕂 به صورت محلی جمع و جور است اگر و تنها اگر آن محدود بعدی به، این است که، ریخت 𝕂 N برای برخی از عدد طبیعی N .

مفاهیم محلی [ ویرایش ]

گفته می شود که یک زیر مجموعه E از یک وکتور توپولوژیکی فضای X است

متقارن اگر - E ⊆ E ، یا معادل آن ، اگر - E = E ؛
متعادل کننده شده اگر TE ⊆ E برای هر عددی {{ریاضی || T | 1 پوند
محدب اگر TE + (1-T ) E ⊆ E برای هر واقعی 0 ≤ T ≤ 1
محدود اگر برای هر محله V از 0 ، سپس E ⊆ TV که تی به اندازه کافی بزرگ است. [7]

تعریف محدودیت می تواند کمی تضعیف شود. E محدود است اگر و فقط اگر هر زیر مجموعه قابل توجهی از آن محدود باشد. همچنین ، E محدود است اگر و فقط اگر برای هر محله متعادل V از 0 ، T وجود دارد که E ⊆ tV . علاوه بر این ، هنگامی که X به صورت محلی محدب باشد ، محدودیت می تواند توسط seminorms مشخص شود : زیر مجموعه E در صورت محدود بودن هر هنجار p مداوم در E محدود است .

هر فضای بردار توپولوژیک دارای یک پایگاه محلی از مجموعه های جذب و متعادل است .

دنباله X • = ( X i )∞
من = 1در TVS X گفته می شود:

کوشی اگر برای هر محله V 0، تفاوت X M - X N متعلق به V که M و N به اندازه کافی بزرگ است.
همگرا مکی 0 اگر وجود دارد یک دنباله از اعداد حقیقی مثبت وجود دارد تحقیق • = ( R i )∞
i = 1واگرایی به ∞ به گونه‌ای است که ( r i x i )∞
i = 1در X به 0 صفر می رسد . [8]

هر دنباله كوچي محدود است ، گرچه ممكن است نت هاي كوچي يا فيلم هاي كوچي محدود نشوند. یک فضای بردار توپولوژیکی که در آن هر توالی کوشی به هم پیوسته متوالی گفته می شود . به طور کلی ، ممکن است کامل نباشد (به این معنا که همه فیلترهای کاشی همگرا می شوند). هر مجموعه کامپکت محدود و کامل است اما اگر TVS Hausdorff نباشد ، زیر مجموعه های جمع و جور لزوما بسته نمی شوند.

منبع

https://en.wikipedia.org/wiki/Topological_vector_space

فضای بردار توپولوژیکی

توسط علی رضا نقش نیلچی | سه شنبه سی و یکم تیر ۱۳۹۹ | 14:34

در ریاضیات ، یک فضای بردار توپولوژیکی (همچنین به آن یک فضای توپولوژیکی خطی گفته می شود ) یکی از ساختارهای اساسی است که در تجزیه و تحلیل عملکردی مورد بررسی قرار می گیرد .

یک فضای بردار توپولوژیکی یک فضای بردار (یک ساختار جبری ) است که یک فضای توپولوژیکی نیز محسوب می شود ، و در نتیجه دومی مفهوم استمرار را می پذیرد . به طور خاص ، فضای توپولوژیکی آن دارای یک ساختار توپولوژیک یکنواخت است و این امکان را فراهم می کند تا یک مفهوم همگرایی یکنواخت فراهم شود .

عناصر فضاهای بردار توپولوژیکی به طور معمول توابع یا اپراتورهای خطی هستند که در فضاهای بردار توپولوژیکی فعالیت می کنند ، و توپولوژی اغلب به گونه ای تعریف می شود که تصور خاصی از همگرایی توالی توابع را به خود اختصاص می دهد.

فضاهای هیلبرت و فضاهای باناخ نمونه خوبی است.

مگر در مواردی که بیان شده باشد ، زمینه اصلی یک فضای بردار توپولوژیکی یا اعداد پیچیده یا عددهای واقعی فرض می شود .

فهرست

تعریف [ ویرایش ]

یک خانواده از محله های مبدأ با دو خاصیت فوق یک فضای بردار توپولوژیکی را مشخص می کنند. سیستم محلات هر نقطه دیگر در فضای بردار با ترجمه بدست می آید .

فضای برداری توپولوژیکی X است فضای برداری بیش از یک حوزه توپولوژیکی 𝕂 (اغلب واقعی یا پیچیده اعداد را با توپولوژی های استاندارد خود) است که با وقف توپولوژی به طوری که علاوه بر بردار X × X → X و اسکالر ضرب 𝕂 × X → X می توابع پیوسته (که در آن حوزه از این توابع با وقف توپولوژی کالا ).

بعضی از نویسندگان (به عنوان مثال ، والتر رودین ) نیاز به توپولوژی در X را T 1 دارند . سپس به این نتیجه می رسد که فضا هاوسدورف و حتی تاچونف است . ساختارهای جبری توپولوژیکی و خطی را می توان با مفروضات اضافی حتی نزدیکتر به هم پیوند داد ، که رایج ترین آنها در زیر ذکر شده است .

دسته فضاهای برداری توپولوژیک بیش از یک میدان توپولوژیکی داده 𝕂 است معمولا با نشان TVS 𝕂 یا TVect 𝕂 . اشیاء فضاهای بردار topological بیش از 𝕂 و morphisms هستند مستمر نقشه 𝕂 خطی از یک شی به دیگری.

راه های تعریف توپولوژی بردار [ ویرایش ]

از آنجایی که هر توپولوژی بردار نادرست ترجمه است (یعنی برای همه x 0 ∈ X ، نقشه X → X تعریف شده توسط x ↦ x 0 + x یک هومومورفیسم است ) ، برای تعریف یک توپولوژی بردار کافی است تا یک مبنای محله (یا فرعی) تعریف شود. برای آن در مبدا

قضیه [1] - فرض کنید که X یک فضای برداری حقیقی یا مختلط است و اجازه دهید ℬ یک مجموعه غیر تهی از زیرمجموعه از X . اگر base یک پایه فیلتر است و شرایط زیر را برآورده می کند:

هر B ∈ ℬ است و متعادل کننده شده و جذب ،
برای هر B ∈ ℬ وجود دارد وجود دارد U ∈ ℬ به طوری که U + U ⊆ B ،

سپس ℬ یک پایگاه محله در 0 برای توپولوژی بردار در X است .

اگر ℬ ارضا بالا دو شرط است، اما نه پایگاه فیلتر و سپس آن را یک محله شکل زیر اساس در 0 (نه فقط بر مبنای محله) برای یک توپولوژی برداری روی X .

مثالها [ ویرایش ]

هر فضای بردار هنجار شده دارای یک ساختار توپولوژیکی طبیعی است : هنجار یک متریک را القا می کند و متریک باعث ایجاد توپولوژی می شود. این یک فضای بردار توپولوژیکی است زیرا:

افزودنی بردار +: X × X → X با توجه به این توپولوژی به طور مشترک مداوم است. این به طور مستقیم از نابرابری مثلث پیروی از هنجار تبعیت می کند.
ضرب مقیاس ·: 𝕂 × X → X ، جایی که field زمینه اسکالار زمینه ای X است ، به طور مشترک پیوسته است. این از نابرابری مثلث و همگن هنجار پیروی می کند.

بنابراین ، تمام فضاهای Banach و فضاهای هیلبرت نمونه ای از فضاهای بردار توپولوژیکی هستند.

فضاهای بردار توپولوژیکی وجود دارد که توپولوژی ناشی از یک هنجار القا نمی شود ، اما هنوز هم به تجزیه و تحلیل علاقه دارند. نمونه هایی از چنین فضاهایی عبارتند از فضاهایی از توابع هولومورفیک در یک دامنه باز ، فضاهای توابع بی نهایت تمایز ، فضاهای شوارتز و فضاهای توابع تست و فضاهای توزیع روی آنها. اینها نمونه هایی از فضاهای مونتل است . فضای نامتناهی مونتل هرگز قابل قبول نیست. وجود یک هنجار برای یک فضای بردار توپولوژیکی معیار با معیار قابلیت پذیری کلموگوروف مشخص می شود .

یک میدان توپولوژیک یک وکتور توپولوژیکی بر روی هر یک از زیر شاخه های آن است .

اگر X یک فضای بردار باشد ، توپولوژی بی اهمیت { X ، ∅ top یک توپولوژی TVS در X است . اگر X یک فضای برداری غیر بدیهی (یعنی غیر 0 بعد) پس از آن است توپولوژی گسسته در X است نه یک توپولوژی TVS؛ علاوه بر این، توپولوژی cofinite در X (که در آن یک زیر مجموعه باز است اگر و تنها اگر مکمل آن محدود است) نیز نمی توپولوژی TVS در X .

عملگر خطی محدود

توسط علی رضا نقش نیلچی | سه شنبه سی و یکم تیر ۱۳۹۹ | 14:12

در تجزیه و تحلیل عملکردی ، یک عملگر خطی محدود یک تحول خطی L : X → Y بین فضاهای بردار توپولوژیکی (TVS) X و X است که زیر مجموعه های محدود از X را به زیر مجموعه های Y محدود می کند . اگر X و Y هستند فضاهای برداری عادی هنجار (نوع خاصی از TVS)، سپس L کراندار است اگر و تنها اگر برخی وجود دارد M ≥ 0 طوری که برای همه ایکس در X ،

|| Lx || Y ≤ M || x || X .

کوچکترین چنین M ، با اشاره | || ل || است، به نام هنجار اپراتور از L .

هر عملگر خطی پیوسته یک عملگر محدود است و علاوه بر این ، یک عملگر خطی بین فضاهای نرمال محدود شده است اگر و فقط اگر مداوم باشد. با این حال ، یک عملگر خطی محدود بین فضای بردار توپولوژیکی کلی تر لزوماً مداوم نیست.

فهرست

اپراتورهای محدود در فضاهای بردار توپولوژیکی [ ویرایش ]

یک عملگر خطی F : X → Y بین دو فضای برداری توپولوژیکی (TVSS) است به صورت محلی محدود و یا فقط محدود اگر هر زمان که B ⊆ X است محدود در X پس از آن F ( B ) در محدود Y . زیرمجموعه TVS اگر هر محله مبدا آن را جذب کند ، محدود (یا به عبارت دقیق تر ، فون نویمان محدود ) نامیده می شود. در یک فضای هنجار (و حتی در یک فضای نیمه کاره)) ، زیرمجموعه فون نویمان محدود است اگر و فقط در صورت محدود بودن هنجار باشد. از این رو ، برای فضاهای دارای هنجار ، مفهوم مجموعه محدود شده فون نویمان با مفهوم معمول یک زیر مجموعه دارای هنجار یکسان است.

هر عملگر خطی مداوم بین TVS یک اپراتور محدود است. اما ، به طور کلی ، یک عملگر خطی محدود بین دو TVS نیاز به مداوم ندارد.

این فرمول به فرد اجازه می دهد تا بین اپراتورهای محدود بین فضاهای بردار توپولوژیکی به عنوان یک اپراتور که مجموعه های محدود به مجموعه های محدود را تعیین می کند ، عملگرهای محدود را مشخص کند. در این زمینه ، هنوز هم صحیح است که هر نقشه پیوسته محدود است ، اما مکالمه شکست می خورد. یک عملگر محدود نباید مداوم باشد. واضح است ، این همچنین بدان معنی است که مرزبندی دیگر معادل استمرار لیپشیتز در این زمینه نیست.

اگر دامنه است فضای bornological (به عنوان مثال pseudometrizable TVS ، یک فضای فریشه ، یک فضای عادی هنجار ) و سپس عملگرهای خطی به هر فضاهای موضعا محدب دیگر این است که اگر محدود و تنها اگر پیوسته است. برای فضاهای LF ، یک مکالمه ضعیف تر وجود دارد. هر نقشه خطی محدود از یک فضای LF پیوسته است .

فضاهای بورنولوژیکی [ ویرایش ]

مقاله اصلی: فضای بورنولوژیک

فضاهای بورنولوژیکی دقیقاً آن فضاهای محدب محلی به ازای هر اپراتور خطی محدود به فضای محدب دیگر محلی لزوماً محدود هستند. بدین معنا که ، یک TVS X محدب محلی به صورت محلی یک فضای تولد است اگر و فقط برای هر TVS Y محدب محلی ، یک عملگر خطی F : X → Y مستمر است اگر و فقط در صورت محدود بودن محدود باشد. [1]

هر فضای هنجار شناسانه ای است.

خصوصیات اپراتورهای خطی محدود [ ویرایش ]

بگذارید F : X → Y یک عامل خطی بین TVS (لزوماً Hausdorff) نباشد. موارد زیر معادل هستند:

F محدود است (به صورت محلی).
(تعریف) F نقشه زیر مجموعه های محدود از حوزه خود به زیر مجموعه های محدود از برد آن؛
نقشه های F زیر مجموعه های دامنه خود را به زیر مجموعه های محدود تصویر خود (Im F : = F ( X محدود می کند .
توالی F توالی های تهی را به توالی محدود انجام می دهد [1]
- دنباله تهی دنباله ای است که به مبدا همگرا می شود.

و اگر X و Y به صورت محلی محدب باشند ، می توانیم به این لیست اضافه کنیم:

نقشه های F دیسک ها را به دیسک های محدود محدود می کند. [2]
نقشه های F -1 دیسکهای زاینده را به دیسکهای زاینده نشان می دهند. [2]

و اگر X یک فضای تولد و Y بصورت محلی محدب است ، می توانیم به این لیست اضافه کنیم:

F پیاپی مداوم است. [3]

عملگرهای خطی محدود شده بین فضاهای نرمال [ ویرایش ]

یک عملگر خطی محدود است به طور کلی یک تابع محدود ، به عنوان به طور کلی یکی می تواند دنباله پیدا X • = ( X i )∞
i = 1در X به این ترتیب $\ displaystyle \ | Lx_ {k} \ | _ {Y} \ rightarrow \ infty$ . در عوض ، تمام آنچه برای محدود کردن اپراتور لازم است این است

$\ displaystyle {\ frac {\ | Lx \ | _ {Y}} {\ | x \ | _ {X}}} \ leq M <\ infty$

برای همه x ≠ 0 . بنابراین ، اپراتور L تنها می تواند یک تابع محدود باشد اگر L ( x ) = 0 را برای همه x برآورده کند ، همانطور که با در نظر گرفتن اینکه برای یک عملگر خطی قابل درک است آسان است $\ displaystyle L (ax) = aL (x)$ برای همه مقیاس ها a . در عوض ، یک عملگر خطی محدود یک عملکرد محلی است .

یک عملگر خطی بین فضاهای نرمال محدود است اگر و فقط در صورت مداوم بودن ، و با خطی بودن ، اگر و فقط اگر در صفر مداوم باشد.

معادل محدودیت و استمرار [ ویرایش ]

همانطور که در مقدمه گفته شد ، یک عملگر خطی L بین فضاهای هنجار X و Y محدود است اگر و تنها اگر یک عملگر خطی مداوم باشد . اثبات به شرح زیر است.

فرض کنید L محدود باشد. سپس ، برای همه بردارها x ، h ∈ X با h nonzero داریم

$\ displaystyle \ | L (x + h) -L (x) \ | = \ | L (ساعت) \ | \ leq M \ | h \ |. \،$

اجازه دادن $\ mathit {ساعت \ ،$ به صفر بروید نشان می دهد که L برابر x است . علاوه بر این ، از آنجا که M ثابت به X وابسته نیست ، این نشان می دهد که در حقیقت L به طور یکنواخت مداوم و حتی Lipschitz مداوم است .

$\ displaystyle \ | Lx \ | = \ left \ Vert {\ | x \ | \ over \ delta} L \ left (\ delta {x \ over \ | x \ |} \ Right) \ Right \ Vert = {\ | x \ | \ over \ delta} \ left \ Vert L \ left (\ delta {x \ over \ | x \ |} \ Right) \ Right \ Vert \ leq {\ | x \ | \ over \ delta \ cdot 1 = {1 \ over \ delta} \ | x \ |.$

این ثابت می کند که L محدود است.

خصوصیات بیشتر [ ویرایش ]

شرط محدود شدن L ، یعنی وجود مقداری M به گونه‌ای که برای همه x وجود داشته باشد

$\ displaystyle \ | Lx \ | \ leq M \ | x \ | ، \ ،$

دقیقاً شرط L است که Lipschitz به طور مداوم در 0 باشد (و از این رو در همه جا ، زیرا L خطی است).

یک روش معمول برای تعریف یک عملگر خطی محدود بین دو فضای Banach داده شده به شرح زیر است. ابتدا یک عملگر خطی را روی یک زیر مجموعه متراکم از دامنه خود تعریف کنید ، به طوری که از نظر محلی محدود باشد. سپس ، اپراتور را به طور مداوم به یک عملگر خطی پیوسته در کل دامنه گسترش دهید .

مثالها [ ویرایش ]

هر عملگر خطی بین دو فضای هنجار محدود بعدی محدود است ، و چنین اپراتور ممکن است به عنوان ضرب توسط برخی ماتریس ثابت مشاهده شود .
هر عملگر خطی تعریف شده بر روی یک فضای هنجاری محدود بعدی محدود است.
در فضای دنباله c 00 در نهایت توالی صفر از اعداد واقعی ، که با هنجار ℓ 1 در نظر گرفته می شود ، عملگر خطی به اعداد واقعی که مبلغ یک دنباله را برمی گرداند محدود شده است ، با هنجار اپراتور 1. اگر همان فضای در نظر گرفته شود با ℓ ∞ هنجار، اپراتور همان است محدود نیست.
بسیاری از تبدیل های داخلی یک اپراتور خطی محدود هستند. به عنوان مثال ، اگر
$K: [a، b] \ بار [c، d] \ to \ mathbb R} \،$
یک تابع مداوم است ، سپس اپراتور L روی فضای C [ a ، b ] توابع پیوسته در [ a ، b ] وقف شده با هنجار یکنواخت و با مقادیر موجود در فضای C [ c ، d ] با L تعریف شده توسط فرمول
$(Lf) (y) = \ int_ {a} ^ {b} \! K (x، y) f (x) \، dx، \،$
محدود است این عملگر در واقع فشرده است . اپراتورهای جمع و جور یک کلاس مهم از اپراتورهای محدود را تشکیل می دهند.
عملگر لاپلاس
$\ Delta: H ^ 2 ({\ mathbb R} ^ n) \ to L ^ 2 ({\ mathbb R} ^ n) \،$
( دامنه آن یک فضای Sobolev است و مقادیر آن را در فضایی از توابع با مربع یکپارچه می کند ) محدود است.
اپراتور تغییر در لیتر 2 فضای از همه توالی ( X 0 ، X 1 ، X 2 ...) از اعداد حقیقی با $x_0 ^ 2 + x_1 ^ 2 + x_2 ^ 2 + \ cdots <\ infty، \،$
$L (x_0 ، x_1 ، x_2 ، \ نقطه) = (0 ، x_0 ، x_1 ، x_2 ، \ نقطه) \ ،$
محدود است هنجار عملگر آن به راحتی 1 مشاهده می شود.

اپراتورهای خطی بدون مرز [ ویرایش ]

هر عملگر خطی بین فضاهای استاندارد محدود نمی شود. بگذارید X فضای همه چند جملهای مثلثاتی باشد که با استفاده از هنجار تعریف شده در [−π، π] باشد

$\ | P \ | = \ int _ {- \ pi} ^ {\ pi} \! | P (x) | \، dx.$

اپراتور L : X → X را که با گرفتن مشتق عمل می کند ، تعریف کنید ، بنابراین یک چند جمله ای P را به مشتق P m خود ترسیم می کنید. سپس ، برای

$v = e ^ {در x}$

با n = 1 ، 2 ، .... ، داریم، $\ | v \ | = 2 \ پی ،$ در حالی که $\ | L (v) \ | = 2 \ pi n \ to \ infty$ به عنوان n → ∞ ، بنابراین این اپراتور محدود نیست.

معلوم است که این یک نمونه مفرد نیست بلکه بخشی از یک قاعده کلی است. با این وجود ، با توجه به هرگونه فضای هنجار X و Y با X نامتناهی و Y فضای صفر نیست ، می توان یک عملگر خطی پیدا کرد که از X تا Y ادامه نداشته باشد.

اینکه چنین عملیاتی اساسی به عنوان مشتق (و دیگران) محدود نیست ، مطالعه را دشوارتر می کند. اما اگر یک دامنه و دامنه اپراتور مشتق با دقت تعریف شود ، ممکن است شخصی نشان داده شود که یک اپراتور بسته است . اپراتورهای بسته عمومی تر از عملگرهای محدود هستند اما هنوز هم از بسیاری جهات "خوب رفتار می کنند".

ویژگی های فضای اپراتورهای خطی محدود [ ویرایش ]

فضای کلیه اپراتورهای خطی محدود از X تا Y توسط (B ( X ، Y مشخص شده و یک فضای بردار نرمال است.
اگر Y Banach باشد ، (B ( X ، Y نیز چنین است .
از این نتیجه می رود که فضاهای دوتایی Banach هستند.
برای هر (A ∈ B ( X ، Y ، هسته A یک فضای فرعی خطی X است .
اگر B ( X ، Y ) Banach باشد و X غیر آنی باشد ، Y آن Banach است.

گرانش ساختاری

توسط علی رضا نقش نیلچی | سه شنبه سی و یکم تیر ۱۳۹۹ | 14:1

گرانش ساختاری نظریه های گرانشی است که تحت تحولات دگرگونی در مفهوم هندسه ریمانی تغییر ناپذیر هستند. دقیق تر ، آنها تحت دگرگونی های ویل ثابت هستند $g _ {{ab}} \ rightarrow \ امگا ^ {2} (x) g _ {{ab}$ جایی که $g_ {ab$ است تانسور متریک و $\ امگا (x)$ یک تابع در است فضازمان .

فهرست

نظریه های مربع ویل [ ویرایش ]

ساده ترین تئوری در این دسته مربع Tensor Wey به عنوان Lagrangian است

${\ mathcal {S}} = \ int \ mathrm {d} ^ {4} x {\ sqrt {-g} C _ {{abcd}} C ^ {{abcd}}،$

جایی که {\ نمایشگر C_ {abcd}} $C _ {c abcd}}$ تانسور Weyl است. این است که با عمل معمول انیشتین - هیلبرت که Lagrangian فقط مقیاس ریکی است در تضاد است . معادله حرکت بر متغیر متریک ، معادله باخ نامیده می شود ،

$\ displaystyle 2 \، \ nabla _ {a} \، \ nabla _ {d} {{C ^ {a}} _ {bc}} ^ {d} + {{C ^ {a}} _ {bc} } ^ {d} R_ {تبلیغ = 0 ،$

جایی که {\ نمایشگر R_ {ab} $R_ {ab$ است تانسور ریچی . معیارهای کاملاً مسطح ، راه حلهای این معادله هستند.

از آنجا که این نظریه ها به معادلات مرتبه چهارم برای نوسانات در پس زمینه ثابت منجر می شوند ، ظاهراً یکسان نیستند. بنابراین به طور کلی اعتقاد بر این است که آنها نمی توانند به طور مداوم اندازه گیری شوند. این اکنون مورد اختلاف است. [1]

نظریه های چهار مشتق [ ویرایش ]

گرانش ساختاری نمونه ای از یک نظریه 4- مشتق است. این بدان معنی است که هر اصطلاح در معادله موج می تواند حداکثر 4 مشتق داشته باشد. نظریه های مثبت و منفی نظریه های 4 مشتق وجود دارد. نکته مثبت این است که نسخه کمی از نظریه همگرا تر و قابل تغییر تر است . نکته منفی این است که ممکن است مسائلی با علیت وجود داشته باشد. مثال ساده تر از معادله موج 4 مشتق معادله موج مقیاس 4 مشتق است:

$\ displaystyle \ operatorname {\ Box} ^ {2} \ Phi = 0$

راه حل این امر در یک میدان مرکزی نیرو عبارت است از:

$\ Phi (r) = 1 - {\ frac {2m} {r}} + ar + br ^ {2$

دو اصطلاح اول برابر با یک معادله موج عادی است. از آنجا که این معادله یک تقریب ساده تر به گرانش کنفورماسی است ، m با جرم منبع مرکزی مطابقت دارد. دو اصطلاح آخر برای معادلات موج 4 مشتق منحصر به فرد است. پیشنهاد شده است که مقادیر اندک به آنها اختصاص داده شود تا ثابت شتاب کهکشانی (که به عنوان ماده تاریک نیز شناخته می شود ) و ثابت انرژی تاریک را تشکیل دهند . [2] راه حل معادل محلول شوارتزیلد در نسبیت عام برای یک منبع کروی برای گرانش کنفورماس متریک با:

$\ displaystyle \ varphi (r) = g ^ {00 = (1-6bc) ^ {\ frac {1} {2}} - {\ frac {2b} {r}} + cr + {\ frac {d 3}} r ^ {2}}$

برای نشان دادن تفاوت بین نسبیت عام. 6bc بسیار کوچک است بنابراین نمی توان نادیده گرفت. مسئله این است که اکنون c کل انرژی جرم منبع است ، b انتگرال فاصله چگالی فاصله از مربع است. بنابراین این یک پتانسیل کاملاً متفاوت برای نسبیت عام است و فقط یک تغییر جزئی نیست.

مسئله اصلی با تئوری های گرانش کنفورماسی و همچنین هر نظریه ای با مشتقات بالاتر ، حضور معمولی ارواح است که به بی ثباتی های نسخه کوانتومی نظریه اشاره دارد ، گرچه ممکن است راه حلی برای مسئله شبح وجود داشته باشد. [3]

یک روش جایگزین این است که ثابت گرانشی را به عنوان میدان تقسیم شکسته تقارن در نظر بگیرید که در این صورت شما تصحیح کوچکی از گرانش نیوتنی را مانند این در نظر خواهید گرفت (جایی که ما در نظر می گیریم $\ varepsilon$ یک اصلاح کوچک:

$\ displaystyle \ operatorname {\ Box} \ Phi + \ varepsilon ^ {2} \ operatorname {\ Box} ^ {2 \ Phi = 0$

در این صورت راه حل کلی همان پرونده نیوتنی است ، مگر اینکه یک عبارت اضافی وجود داشته باشد:

$left \ displaystyle \ Phi = 1 - {\ frac {2m} {r}} سمت چپ (1+ \ alpha \ sin \ left (+ \ frac {r} {\ varepsilon}} + \ beta \ Right) \ Right) }$

جایی که یک مؤلفه اضافی وجود دارد که از نظر سینوسی از فضا متفاوت است. طول موج این تغییر می تواند بسیار بزرگ باشد مانند عرض اتمی. بنابراین به نظر می رسد چندین پایدار پایدار در اطراف یک نیروی گرانشی در این مدل وجود دارد.

وحدت سازه با مدل استاندارد [ ویرایش ]

این تئوری با افزودن یک اصطلاح گرانشی مناسب به عملکرد مدل استاندارد در زمان خمیده ، یک عدم تغییر شکل محلی (ویل) را ایجاد می کند. سنج مخروطی با انتخاب مقیاس جرمی مرجع بر اساس ثابت اتصال جفت ثابت شده است. این روش توده ها را برای بوزون های بردار و زمینه های ماده مشابه مکانیسم هیگز ایجاد می کند بدون تقارن تقارن خود به خود سنتی. [4]

منبع

https://en.wikipedia.org/wiki/Conformal_gravity

شعاع طیفی

توسط علی رضا نقش نیلچی | دوشنبه سی ام تیر ۱۳۹۹ | 15:17

در ریاضیات ، شعاع طیفی یک ماتریس مربع یا یک عملگر خطی محدود ، بزرگترین مقدار مطلق مقادیر ویژه آن است (یعنی supremum در بین مقادیر مطلق عناصر در طیف آن ). بعضی اوقات توسط ρ مشخص می شود.

فهرست

ماتریس [ ویرایش ]

بگذارید λ 1 ، ... ، λ n ، ارزش ویژه ( واقعی یا پیچیده ) یک ماتریس A ∈ C n � n باشد. سپس شعاع طیفی آن( ρ ( A تعریف می شود:

$\ displaystyle \ rho (A) = \ max \ left \ {| \ lambda _ {1} |، \ dotsc، | \ lambda _ {n} | \ Right \}$

تعداد شرط از{\ نمایشگر A} $آ$ را می توان با استفاده از شعاع طیفی بیان کرد $\ displaystyle \ rho (A) \ rho (A ^ {- 1})}$ .

شعاع طیفی نوعی از کمترین میزان هنجارهای یک ماتریس است. از یک طرف ، $\ displaystyle \ rho (A) \ leqslant \ | A \ |}$ برای هر هنجار ماتریس طبیعی $\ | \ cdot \ |$ و از طرف دیگر فرمول گلفند این را بیان می کند $\ displaystyle \ rho (A) = \ lim _ {k \ to \ infty} \ | A ^ {k} \ | ^ {1 / k}$ ؛ هر دو این نتایج در زیر نشان داده شده است. با این حال ، شعاع طیفی لزوما راضی نیست $\ displaystyle \ | A \ mathbf {v} \ | \ leqslant \ rho (A) \ | \ mathbf {v} \ |}$ برای بردارهای دلخواه $\ displaystyle \ mathbf {v} \ in \ mathbb {C} ^ {n}$ . برای دیدن دلیل ، اجازه دهید $\ displaystyle r> 1$ خودسرانه باشید و ماتریس را در نظر بگیرید $\ displaystyle C_ {r} = {\ fill pmatrix} 0 & r ^ {- 1} \\ r & 0 \ end {pmatrix}}$ . چند جمله ای مشخصه از ${\ صفحه نمایش C_ {r}$ است $\ displaystyle \ lambda ^ {2} -1}$ ، از این رو مقادیر خاص آن هستند $ساعت 1 بعد از ظهر 1$ ، و بنابراین $\ displaystyle \ rho (C_ {r}) = 1$ . با این حال $\ displaystyle C_ {r} \ mathbf {e} _ {1} = r \ mathbf {e} _ {2}}$ ، بنابراین $\ displaystyle \ | C_ {r} \ mathbf {e} _ {1} \ | = r> 1 = \ rho (C_ {r}) \ | \ mathbf {e} _ {1} \ |}$ برای $\ displaystyle \ | \ cdot \ |}$ هر کسی بودن $\ displaystyle \ ell ^ {p}}$ هنجار در $\ mathbb {C} ^ n$ . آنچه هنوز اجازه می ده $\ displaystyle \ | C_ {r} ^ {k} \ | ^ {1 / k} \ به 1$ مانند $k \ to \ infty$ این است که $\ displaystyle C_ {r} ^ {2} = I$ ، ساخت $\ displaystyle \ | C_ {r} ^ {k} \ | ^ {1 / k} \ leqslant \ | C_ {r} \ | ^ {1 / k} = r ^ {1 / k} \ to 1$ مانند $k \ to \ infty$ .

$\ displaystyle \ | A \ mathbf {v} \ | \ leqslant \ rho (A) \ | \ mathbf {v} \ |}$ برای همه $\ displaystyle \ mathbf {v} \ in \ mathbb {C} ^ {n}$

چه موقع نگه دارد $آ$ یک ماتریس هرمیتی و $\ displaystyle \ | \ cdot \ |}$ است هنجار اقلیدسی .

نمودارها [ ویرایش ]

شعاع طیفی از یک نمودار محدود تعریف شده است که شعاع طیفی از ماتریس مجاور آن است .

این تعریف در مورد نمودارهای نامتناهی با درجه های محدود vertices گسترش می یابد (یعنی تعداد واقعی C وجود دارد به گونه ای که درجه هر راس نمودار از C کوچکتر است ). در این حالت ، برای نمودار G تعریف کنید:

$\ ell ^ {2} (G) = \ left \ {f: V (G) \ to {\ mathbf {R}} \: \ \ sum \ nolimits _ {{v \ in V (G)}} \ left \ | f (v) ^ {2} \ Right \ | <\ infty \ Right \.$

بگذارید γ عامل مجاور G باشد :

${\ شروع {موارد} \ gamma: \ ell ^ {2} (G) \ to \ ell ^ {2} (G) \\ (\ gamma f) (v) = \ sum _ {{(u، v) \ در E (G)} f (u) \ end {موارد}$

شعاع طیفی G تعریف می شود شعاع طیفی از محدود عملگر خطی γ .

حد بالایی [ ویرایش ]

مرزهای بالا برای شعاع طیفی یک ماتریس [ ویرایش ]

گزاره زیر یک حد بالایی ساده و در عین حال مفید برای شعاع طیفی یک ماتریس را نشان می دهد:

قضیه. بگذارید A ∈ C n � n با شعاع طیفی ρ ( A ) و یک هنجار ماتریس سازگار || ⋅ || . سپس برای هر عدد صحیح $\ displaystyle k \ geqslant 1$ :

$\ rho (A) \ leq \ | A ^ {k} \ | ^ {\ frac {1} {k}.$

اثبات

بگذارید ( v ، λ ) یک جفت eigenveector - eigenvalue برای یک ماتریس A باشد. با خاصیت زیر ضرب از هنجار ماتریس ، دریافت می کنیم:

$| \ lambda | ^ {k} \ | \ mathbf {v} \ | = \ | \ lambda ^ {k} \ mathbf {v} \ | = \ | A ^ {k} \ mathbf {v} \ | \ leq \ | A ^ {k} \ | \ cdot \ | \ mathbf {v} \ |$

و از v 0 ما داریم

$| \ lambda | ^ {k} \ leq \ | A ^ {k} \ |$

و بنابراین

$\ rho (A) \ leq \ | A ^ {k} \ | ^ {\ frac {1} {k}.$

مرزهای بالا برای شعاع طیفی از یک نمودار [ ویرایش ]

بسیاری از مرزهای بالایی برای شعاع طیفی از نمودار از نظر تعداد آن وجود دارد N از رئوس و تعداد آن متر از لبه. به عنوان مثال ، اگر

$\ displaystyle {\ frac {(k-2) (k-3)} {2}} \ leq mn \ leq {\ frac {k (k-3)} {2}}}$

جایی که $\ displaystyle 3 \ leq k \ leq n$ یک عدد صحیح است ، سپس [1]

$\ displaystyle \ rho (G) \ leq {\ sqrt {2m-n-k + {\ frac {5} {2}} + {\ sqrt {2m-2n + {\ frac {9} {4}}}} }$

دنباله قدرت [ ویرایش ]

قضیه [ ویرایش ]

شعاع طیفی ارتباط نزدیکی با رفتار همگرایی توالی قدرت یک ماتریس دارد. یعنی ، قضیه زیر وجود دارد:

قضیه بگذارید A ∈ C n � n با شعاع طیفی ρ ( A ) . سپس ρ ( A ) <1 اگر و فقط اگر

$\ lim _ {k \ to \ infty} A ^ {k} = 0.$

از طرف دیگر ، اگر ρ ( A )> 1 $\ displaystyle \ lim _ {k \ to \ infty} \ | A ^ {k} \ | = \ infty$ . این بیانیه برای هر انتخاب هنجار ماتریس در C n � n در نظر گرفته شده است .

اثبات قضیه [ ویرایش ]

فرض کنید حد مورد نظر صفر باشد ، نشان خواهیم داد که ρ ( A ) <1 . بگذارید ( v ، λ ) یک جفت eigenveector - eigenvalue برای A باشد. از آنجا که A k v = λ k v داریم:

${\ شروع {تراز وسط 0 & = \ left (\ lim _ {k \ to \ infty} A ^ {k} \ Right) \ mathbf {v} \\ & = \ lim _ {k \ to \ infty} \ left (A ^ {k} \ mathbf {v} \ درست) \\ & = \ lim _ {k \ به \ infty} \ lambda ^ {k} \ mathbf {v} \\ & = \ mathbf {v} \ lim _ {k \ to \ infty} \ lambda ^ {k} \ end {تراز شده}$

و از آنجا که با فرضیه 0 v ، باید داشته باشیم

$\ lim _ {k \ to \ infty} \ lambda ^ {k} = 0$

که دلالت دارد | λ | <1. از آنجا که این باید برای هر مقدمه ای صحیح باشد ، می توانیم نتیجه بگیریم ρ ( A ) <1.

حال فرض کنید که شعاع A کمتر از 1 است . از قضیه فرم عادی جردن ، می دانیم که برای همه A ∈ C n � n ، V ، J ∈ C n � n با V غیر مفرد و J بلوک مورب وجود دارد به گونه ای که:

$A = VJV ^ {- 1$

با

$J = {\ آغاز {bmatrix} J_ {m_ {1}} (\ lambda _ {1}) & 0 & 0 & \ cdots & 0 \\ 0 & J_ {m_ {2}} (\ lambda _ {2}) & 0 & \ cdots & 0 \\ \ vdots & \ cdots & \ ddots & \ cdots & \ vdots \\ 0 & \ cdots & 0 & J_ {m_ {s-1}} (\ lambda _ {s-1}) & 0 \\ 0 & \ cdots & \ cdots & 0 & J_ {m_ {s}} (\ lambda _ {s}) \ end {bmatrix}$

جایی که

$J_ {m_ {i} \ (\ lambda _ {i}) = {\ fill {bmatrix \ lambda _ {i} & 1 & 0 & \ cdots & 0 \\ 0 & \ lambda _ {i} & 1 & \ cdots & 0 \** vdots & \ vdots & \ ddots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & \ lambda _ {i} & 1 \\ 0 & 0 & \ cdots & 0 & \ lambda _ {i} \ end {bmatrix} \ in \ mathbf {C} ^ {m_ {i} \ بار m_ {i}} ، 1 \ leq i \ leq s.$

دیدن آن بسیار آسان است

$A ^ {k} = VJ ^ {k} V ^ {- 1$

و از آنجا که J مورب است ،

$J ^ {k} = {\ آغاز {bmatrix} J_ {m_ {1}} ^ {k} (\ lambda _ {1}) & 0 & 0 & \ cdots & 0 \\ 0 & J_ {m_ {2}} ^ {k} (\ lambda _ {2}) & 0 & \ cdots & 0 \\* vdots & \ cdots & \ ddots & \ cdots & \ vdots \\ 0 & \ cdots & 0 & J_ {m_ {s-1} ^ {k} (\ lambda _ {s -1}) & 0 \\ 0 & \ cdots & \ cdots & 0 & J_ {m_ {s}} ^ {k} (\ lambda _ {s}) \ end {bmatrix}$

در حال حاضر ، یک نتیجه استاندارد در قدرت $m_ {i} \ بار m_ {i$ اردن بلوک اظهار داشت که ، برای $k \ geq m_ {i} -1$ :

$J_ {m_ {i} {^ {k} (\ lambda _ {i}) = {\ fill bmatrix \ lambda _ {i} ^ {k} & {k \ 1 1 choose \ lambda _ {i} ^ k-1} & {k \ انتخاب 2} \ lambda _ {i} ^ {k-2} & \ cdots & c k \ انتخاب m_ {i} -1} \ lambda _ {i} ^ {k-m_ {i} +1} \\ 0 & \ lambda _ {i} ^ {k} & {k \ انتخاب 1} \ lambda _ {i} ^ {k-1} & \ cdots & {k \ انتخاب m_ {i -2} \ lambda _ {i} ^ {k-m_ {i} +2 \\\ vdots & \ vdots & \ ddots & \ ddots & \ vdots \\ 0 & 0 & cdots & \ lambda _ {i} ^ { k} & {k \ انتخاب 1} \ lambda _ {i} ^ {k-1} \\ 0 & 0 & \ cdots & 0 & \ lambda _ {i} ^ {k} \ end {bmatrix}$

بنابراین ، اگر $\ rho (A) <1$ پس برای همه $| \ lambda _ {i} | <1$ . از این رو برای همه من :

$\ lim _ {{k \ to \ infty}} J _ {{m_ {i}}} ^ {k} = 0$

که نشان می دهد

$\ lim _ {{k \ to \ infty}} J ^ {k} = 0.$

از این رو،

$\ lim _ {\ k \ to \ infty}} A ^ {k} = \ lim _ {{k \ to \ infty}} VJ ^ {k} V ^ {{- 1}} = V \ left (\ lim _ {{k \ به \ infty}} J ^ {k} \ درست) V ^ {{- 1}} = 0$

از طرف دیگر ، اگر $\ rho (A)> 1$ ، حداقل یک عنصر در J وجود دارد که با افزایش k ، محدود نمی ماند ، بنابراین بخش دوم بیانیه را اثبات می کند.

فرمول گلفند [ ویرایش ]

قضیه [ ویرایش ]

قضیه بعدی شعاع طیفی را به عنوان حد هنجارهای ماتریس می دهد.

قضیه (فرمول گلفند ؛ 1941). برای هر هنجار ماتریس || ⋅ || ، داریم

$\ rho (A) = \ lim _ {{k \ to \ infty}} \ left \ | A ^ {k} \ Right \ | ^ {{{\ frac {1} {k}}}.$ [2] .

اثبات [ ویرایش ]

برای هر ε > 0 ، ابتدا دو ماتریس زیر را می سازیم:

$A _ {{\ pm}} = {\ frac {1 {{\ rho (A) \ pm \ varepsilon}} A.$

سپس:

$\ rho \ left (A _ {{\ pm}} \ Right) = {\ frac {\ rho (A) {\ rho (A) \ pm \ varepsilon}}، \ qquad \ rho (A _ {+}) < 1 <\ rho (A _ {-}).$

ابتدا قضیه قبلی را روی A اعمال می کنیم :

$\ lim _ {{k \ to \ infty}} A _ {+} ^ {k} = 0.$

به این معنی که با تعریف حد توالی ، N ∈ N وجود دارد به گونه ای که برای همه k ≥ N ،

$\ displaystyle {\ شروع {تراز شده} \ چپ \ | A _ {+} ^ {k} \ Right \ | <1 \ end {تراز وسط}}$

بنابراین

$\ displaystyle {\ شروع {تراز شده} \ چپ \ | A ^ {k} \ درست \ | ^ {\ frac {1} {k}} <\ rho (A) + \ varepsilon. \ end {تراز شده$

استفاده از قضیه قبلی در A - دلالت دارد $\ | A _ {-} ^ {k} \ |$ محدود نیست و N - ∈ N وجود دارد به گونه ای که برای همه k ≥ N - ،

$\ displaystyle {\ شروع {تراز شده} \ چپ \ | A _ {-} ^ {k} \ Right \ |> 1 \ end {تراز شده}}}$

بنابراین

$\ displaystyle {\ شروع {تراز شده} \ چپ \ | A ^ {k} \ درست \ | ^ {\ frac {1} {k}}> \ rho (A) - \ varepsilon. \ end {تراز شده}}$

بگذارید N = max { N ، N - } باشد ، پس باید:

$\ displaystyle \ forall \ varepsilon> 0 \ quad \ n N \ in \ mathbf {N} \ quad \ forall k \ geq N \ quad \ rho (A) - \ varepsilon <\ left \ | A ^ {k} \ راست \ | ^ {\ frac {1} {k}} <\ rho (A) + \ varepsilon$

که طبق تعریف

$\ lim _ {\ k \ to \ infty}} \ left \ | A ^ {k} \ Right \ | ^ {{{\ frac {1} {k}}}} = \ rho (A).$

نتیجه گیری های گلفند [ ویرایش ]

فرمول گلفند مستقیماً به مرز شعاع طیفی از محصولاتی که ماتریسهای بسیار ظریف دارند محدود می شود ، یعنی با فرض اینکه همه آنها رفت و آمد می کنند.

$\ rho (A_ {1} \ cdots A_ {n}) \ leq \ rho (A_ {1}) \ cdots \ rho (A_ {n}).$

در واقع ، اگر هنجار سازگار باشد ، اثبات بیش از پایان نامه نشان می دهد. در حقیقت ، با استفاده از لیم قبلی ، می توانیم در حد تعیین شده ، حد پایین سمت چپ را با شعاع طیفی جایگزین کنیم و دقیق تر بنویسیم:

$\ forall \ varepsilon> 0، \ وجود N \ in m \ mathbf {N}} ، \ forall k \ geq N \ quad \ rho (A) \ leq \ | A ^ {k} \ | ^ {{{\ frac 1} {k}}}} <\ rho (A) + \ varepsilon$

که طبق تعریف

$\ displaystyle \ lim _ {k \ to \ infty} \ left \ | A ^ {k} \ Right \ | ^ {\ frac {1} {k}} = \ rho (A) ^ {+}،}$

جایی که به این معنی است که از بالا به حد مجاز رسیده است.

مثال [ ویرایش ]

ماتریس را در نظر بگیرید

$A = {\ fill bmatrix} 9 & -1 & 2 \\ - 2 & 8 & 4 \\ 1 & 1 & 8 \ end {bmatrix$

مقادیر ویژه آنها 5 ، 10 ، 10 است . با تعریف ، ρ ( A ) = 10 . در جدول زیر ، مقادیر $\ | A ^ {k} \ | ^ {{{\ frac {1} {k}}}}$ برای چهار هنجار استفاده شده در مقابل چندین مقدار افزایش k ذکر شده است (توجه داشته باشید که به دلیل شکل خاص این ماتریس ، $\ |. \ | _ {1} = \ |. \ | _ {\ infty$ ):

ک	$\ \|. \ \| _ {1} = \ \|. \ \| _ {\ infty$	$\ \|. \ \| _ {F}$	$\ \|. \ \| _ {2$
1	14	15.362291496	10.681145748
2	12.649110641	12.328294348	10.595665162
3	11.934831919	11.532450664	10.500980846
4	11.501633169	11.151002986	10.418165779
5	11.216043151	10.921242235	10.351918183
$\ vdots$	$\ vdots$	$\ vdots$	$\ vdots$
10	10.604944422	10.455910430	10.183690042
11	10.548677680	10.413702213	10.166990229
12	10.501921835	10.378620930	10.153031596
$\ vdots$	$\ vdots$	$\ vdots$	$\ vdots$
20	10.298254399	10.225504447	10.091577411
30	10.197860892	10.149776921	10.060958900
40	10.148031640	10.112123681	10.045684426
50	10.118251035	10.089598820	10.036530875
$\ vdots$	$\ vdots$	$\ vdots$	$\ vdots$
100	10.058951752	10.044699508	10.018248786
200	10.029432562	10.022324834	10.009120234
300	10.019612095	10.014877690	10.006079232
400	10.014705469	10.011156194	10.004559078
$\ vdots$	$\ vdots$	$\ vdots$	$\ vdots$
1000	10.005879594	10.004460985	10.001823382
2000	10.002939365	10.002230244	10.000911649
3000	10.001959481	10.001486774	10.000607757
$\ vdots$	$\ vdots$	$\ vdots$	$\ vdots$
10000	10.000587804	10.000446009	10.000182323
20000	10.000293898	10.000223002	10.000091161
30000	10.000195931	10.000148667	10.000060774
$\ vdots$	$\ vdots$	$\ vdots$	$\ vdots$
100000	10.000058779	10.000044600	10.000018232

عملگرهای خطی محدود [ ویرایش ]

برای یک عملگر خطی A محدود و هنجار اپراتور || � || ، مجدداً داریم

$\ rho (A) = \ lim _ {{k \ to \ infty}} \ | A ^ {k} \ | ^ {{{\ frac {1} {k}}}.$

اگر شعاع طیفی آن با شعاع عددی آن همزمان باشد ، یک عملگر محدود (در یک فضای پیچیده هیلبرت) به عنوان یک عملگر طیفی شناخته می شود . نمونه ای از چنین اپراتور یک اپراتور معمولی است .

منابع

https://en.wikipedia.org/wiki/Spectral_radius

روش ژاکوبی

توسط علی رضا نقش نیلچی | دوشنبه سی ام تیر ۱۳۹۹ | 14:10

در جبر خطی عددی ، روش Jacobi یک الگوریتم تکراری برای تعیین راه حل های یک سیستم کاملاً مورب غالب از معادلات خطی است . هر عنصر مورب حل شده است و یک مقدار تقریبی به آن وصل می شود. فرآیند تا زمانی که همگرا شود تکرار می شود. این الگوریتم یک نسخه سلب شده از روش تبدیل جاکوبی از مورب مورباسیون است . این روش به نام کارل گوستاو ژاکوب ژاکوبی نامگذاری شده است .

فهرست

توضیحات [ ویرایش ]

اجازه دهید

$A \ mathbf {x} = \ mathbf {b$

یک سیستم مربع از معادلات خطی n ، که در آن:

$A = {\ fill bmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn \ end {bmatrix}}، \ qquad \ mathbf {x} = {\ fill bmatrix} x_ {1} \\ x_ {2 } \\\ vdots \\ x_ {n} \ end {bmatrix}}، \ qquad \ mathbf {b} = {\ fill bmatrix} b_ {1 \\ b_ {2} \\\ vdots \\ b_ { n} \ end {bmatrix.$

سپس را می توان به تجزیه مورب جزء D ، یک قسمت پایین مثلثی L و بخش مثلثی بالای U :

$\ displaystyle A = D + L + U \ qquad {\ text {جایی که}} \ qquad D = {\ fill {bmatrix} a_ {11} & 0 & \ cdots & 0 \\ 0 & a_ {22} & \ cdots & 0 \\\ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & a_ {nn} \ end {bmatrix}} {\ text {و} + L + U = {\ شروع {bmatrix 0 & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & 0 & cdots & a_ {2n} \\\ vdots & \ vdots & \ dots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & 0 \ end {bmatrix}. }$

سپس محلول به صورت تکراری از طریق بدست می آید

$\ displaystyle \ mathbf {x} ^ {(k + 1)} = D ^ {- 1} (\ mathbf {b} - (L + U) \ mathbf {x} ^ {(k)})،}$

جایی که $\ mathbf {x} ^ {(k)$ است ک هفتم تقریب و یا تکرا $\ mathbf {x$ و $\ mathbf {x} ^ {(k + 1)$ تکرار بعدی یا k + 1 است $\ mathbf {x$ . فرمول مبتنی بر عنصر بدین ترتیب است:

$x_ {i} ^ {(k + 1)} = {\ frac {1} {a_ {ii}}} \ سمت چپ (b_ {i} - \ sum _ {j \ neq i} a_ {ij} x_ {j } ^ {(k) right \ درست) ، \ quad i = 1،2 ، \ ldots ، n.$

محاسبه $\ displaystyle x_ {i} ^ {(k + 1)}}$ نیاز به هر عنصر در x ( k ) به جز خود دارد. برخلاف روش گاوس-سییدل ، ما نمی توانیم بازنویسی کنیم $\ displaystyle x_ {i} ^ {(k)$ با $\ displaystyle x_ {i} ^ {(k + 1)}}$ ، زیرا این مقدار توسط بقیه محاسبات مورد نیاز خواهد بود. حداقل مقدار ذخیره سازی دو بردار اندازه n است .

الگوریتم [ ویرایش ]

ورودی:  حدس اولیهبه محلول ، (مورب غالب مورب)
  
      
، وکتور سمت راست   
، معیار همگرایی
 خروجی:  راه حل هنگامی که همگرایی حاصل شد 
نظرات:  شبه کد بر اساس فرمول مبتنی بر عنصر فوق


در حالی که همگرایی رسیده است انجام 
    برای من: = 1 مرحله تا N انجام

        برای j: = 1 مرحله تا زمانی که n do انجام دهم 
            اگر j ≠ i باشد

            پایان 
        پایان

    پایان

پایان

همگرایی [ ویرایش ]

شرط همگرایی استاندارد (برای هر روش تکراری) زمانی است که شعاع طیفی ماتریس تکرار کمتر از 1 باشد:

$\ displaystyle \ rho (D ^ {- 1} (L + U)) <1.$

شرط کافی (اما لازم نیست) برای همگرایی روش این است که ماتریس A کاملاً یا غیرقابل برگشت به صورت مورب مسلط است . تسلط مورب سخت گیرانه به این معنی است که برای هر سطر ، مقدار مطلق اصطلاح مورب از مجموع مقادیر مطلق سایر اصطلاحات بیشتر است:

$\ سمت چپ | a_ {ii} \ Right |> \ sum _ {j \ neq i} {\ left | a_ {ij} \ Right |.$

روش ژاکوبی حتی اگر این شرایط راضی نباشد گاهی همگرا می شود.

توجه داشته باشید که روش Jacobi برای هر ماتریس مثبت مثبت متقارن همگرا نیست . مثلا

$\ displaystyle A = {\ fill {pmatrix} 29 & 2 & 1 \\ 2 & 6 & 1 \\ 1 & 1 & {\ frac {1} {5}} \ end {pmatrix}} \ quad \ Rightarrow \ quad D ^ {- 1} (L + U ) = {\ fill pmatrix} 0 & {\ frac {2} 29}} & {\ frac {1 {29}} \\ {\ frac {1} {3}} & 0 & {\ frac {1} 6}} \\ 5 & 5 & 0 \ end {pmatrix} \ quad \ Rightarrow \ quad \ rho (D ^ {- 1} (L + U)) \ تقریبا 1.0661 \ ،.}$

مثال [ ویرایش ]

یک سیستم خطی از فرم $تبر = ب$ با برآورد اولیه $x ^ {{(0)}}$ از رابطه زیر بدست می آید

$A = {\ fill bmatrix} 2 & 1 \\ 5 & 7 \\ end {bmatrix}}، \ b = {\ fill bmatrix} 11 \\ 13 \* end {bmatrix} \ quad {\ متن {و} } \ quad x ^ {(0) = {\ fill bmatrix} 1 \\ 1 \\\ end {bmatrix.$

ما از معادله استفاده می کنیم $\ displaystyle x ^ {(k + 1)} = D ^ {- 1} (b- (L + U) x ^ {(k)})$ ، در بالا شرح داده شده ، برای برآورد $ایکس$ . ابتدا معادله را به روشی راحت تر بازنویسی می کنیم $\ displaystyle D ^ {- 1} (b- (L + U) x ^ {(k)}) = Tx ^ {(k) + C$ ، جایی که $\ displaystyle T = -D ^ {- 1} (L + U)$ و $C = D ^ {- 1} b$ . از مقادیر شناخته شده

$D ^ {- 1} = {\ fill {bmatrix} 1/2 & 0 \\ 0 & 1/7 \\ end end {bmatrix}}، \ L = {\ fill bmatrix 0 & 0 \\ 5 & 0 \\ end end {bmatrix } \ quad {\ text و}} \ quad U = begin \ آغاز {bmatrix} 0 & 1 \\ 0 & 0 \\ end {bmatrix}.$

ما تعیین می کنیم $T = -D ^ {- 1} (L + U)$ مانند

$T = {\ fill bmatrix} 1/2 & 0 \\ 0 & 1/7 \\\ end {bmatrix}} \ left \ {begin \ fill {bmatrix 0 & 0 \\ - 5 & 0 \ end end {bmatrix}} + {\ fill bmatrix} 0 & -1 \\ 0 & 0 \\\ end {bmatrix} \ Right \} = {\ fill bmatrix 0 & -1 / 2 \\ - 5/7 & 0 \\\ end {bmatrix}.$

به علاوه، $ج$ به عنوان یافت می شود

$C = {\ fill bmatrix} 1/2 & 0 \\ 0 & 1/7 \\\ end {bmatrix}} {\ fill bmatrix} 11 \\ 13 \\ end end {bmatrix} = {\ fill {bmatrix 11 / 2 \\ 13/7 \\\ end {bmatrix.$

با $تی$ و $ج$ محاسبه شده ، ما تخمین می زنیم $ایکس$ مانند $x ^ {(1) = Tx ^ {(0)} + C$ :

$x ^ {(1) = {\ آغاز {bmatrix} 0 & -1 / 2 \\ - 5/7 & 0 \\\ end {bmatrix}} {\ fill bmatrix 1 \\ 1 \\ end {bmatrix } + {\ fill bmatrix} 11/2 \\ 13/7 \\ end end {bmatrix}} = {\ fill {bmatrix} 5.0 \\ 8/7 \** end {bmatrix} \ تقریبی {\ آغاز bmatrix} 5 \\ 1.143 \\* end {bmatrix}.$

تکرار بعدی بازده است

$x ^ {(2) = {\ fill bmatrix} 0 & -1 / 2 \\ - 5/7 & 0 \\\ end {bmatrix}} {\ fill bmatrix} 5.0 \\ 8/7 \\ end end bmatrix}} + {\ fill bmatrix} 11/2 \\ 13/7 \\\ end {bmatrix}} = {\ fill bmatrix 69/14 \ - - 12/7 \\ end end {bmatrix \ تقریبی {\ آغاز {bmatrix 9 4.929 \ - 1.714 \\\ end {bmatrix}.$

این روند تا همگرایی تکرار می شود (یعنی تا زمانی که $\ | تبر ^ {(ن) - b \ |$ کوچک است) راه حل پس از 25 تکرار است

$x = {\ fill bmatrix} 7.111 \\ - 3.222 \ end {bmatrix.$

مثال دیگر [ ویرایش ]

فرض کنید سیستم خطی زیر به ما داده می شود:

${\ شروع {تراز شده} 10x_ {1} -x_ {2} + 2x_ {3} & = 6، \\ - x_ {1} + 11x_ {2} -x_ {3} + 3x_ {4} & = 25، \\ 2x_ {1} -x_ {2} + 10x_ {3} -x_ {4} & = - 11، \\ 3x_ {2} -x_ {3} + 8x_ 4} & = 15. \ end {تراز شده }$

اگر (0 ، 0 ، 0 ، 0) را به عنوان تقریب اولیه انتخاب کنیم ، سپس اولین راه حل تقریبی توسط

$\ displaystyle {\ شروع {تراز شده} x_ {1} & = (6 + 0- (2 * 0)) / 10 = 0.6 ، \\ x_ {2} & = (25 + 0 + 0- (3 * 0 )) / 11 = 25/11 = 2.2727 ، \\ x_ {3} & = (- 11- (2 * 0) + 0 + 0) /10=-1.1 ، \\ x_ {4} & = (15- (3 * 0) +0) /8=1.875.*end {تراز شده}}}$

با استفاده از تقریبهای به دست آمده ، روش تکراری تا رسیدن به دقت مطلوب تکرار می شود. در زیر راه حل های تقریبی بعد از پنج تکرار است.

$x_ {1$	$x_ {2$	$x_ {3$	$x_ {4$
0.6	2.27272	-1.1	1.875
1.04727	1.7159	-0.80522	0.88522
0.93263	2.05330	-1.0493	1.13088
1.01519	1.95369	-0.9681	0.97384
0.98899	2.0114	-1.0102	1.02135

راه حل دقیق سیستم (1 ، 2 ، −1 ، 1) است .

مثالی با استفاده از پایتون و نامپی [ ویرایش ]

روش عددی زیر به سادگی برای تولید بردار راه حل تکرار می کند.

def jacobi(A, b, x_init, epsilon=1e-10, max_iterations=500):
    D = np.diag(np.diag(A))
    LU = A - D
    x = x_init
    for i in range(max_iterations):
        D_inv = np.diag(1 / np.diag(D))
        x_new = np.dot(D_inv, b - np.dot(LU, x))
        if np.linalg.norm(x_new - x) < epsilon:
            return x_new
        x = x_new
    return x

# problem data
A = np.array([
    [5, 2, 1, 1],
    [2, 6, 2, 1],
    [1, 2, 7, 1],
    [1, 1, 2, 8]
])
b = np.array([29, 31, 26, 19])

# you can choose any starting vector
x_init = np.zeros(len(b))
x = jacobi(A, b, x_init)

print('x:', x)
print('computed b:', np.dot(A, x))
print('real b:', b)

Produces the output:

x: [3.99275362 2.95410628 2.16183575 0.96618357]
computed b: [29. 31. 26. 19.]
real b: [29 31 26 19]

روش ژاکوبی وزنی [ ویرایش ]

تکرار وزنی ژاکوبی از یک پارامتر استفاده می کند $\ امگا$ برای محاسبه تکرار به عنوان

$\ displaystyle \ mathbf {x} ^ {(k + 1)} = \ omega D ^ {- 1} (\ mathbf {b} - (L + U) \ mathbf {x} ^ {(k)}) + \ سمت چپ (1- \ امگا \ راست) \ mathbf {x} ^ {(k)}$

با $\ امگا = 2/3$ انتخاب معمول بودن [1]

همگرایی در مورد قطعی مثبت متقارن [ ویرایش ]

در صورتی که ماتریس سیستم $آ$ از نوع متقارن مثبت است که می تواند همگرایی را نشان دهد.

اجازه دهید $\ displaystyle C = C _ {\ omega} = I- \ omega D ^ {- 1} A}$ ماتریس تکرار باشد. سپس ، همگرایی برای آن تضمین شده است

$\ displaystyle \ rho (C _ {\ omega) <1 \ quad \ Longleftrightarrow \ quad 0 <\ omega <{\ frac {2} {\ lambda _ {\ text {max}} (D ^ {- 1} A )}} \،$

جایی که $\ displaystyle \ lambda _ {\ text {حداکثر}}}$ حداکثر ارزش ویژه است.

شعاع طیفی را می توان برای انتخاب خاص از به حداقل رساند $\ displaystyle \ omega = \ omega _ {\ text {opt}}$ به شرح زیر است

$\ displaystyle \ min _ {\ omega} \ rho (C _ {\ omega) = \ rho (C _ {\ omega _ {\ text {opt}}}) = 1 - {\ frac {2} {\ kappa ( D ^ {- 1} A) +1}} \ quad {\ text {برای}} \ quad \ omega _ {\ متن {opt}}: = {\ frac {2} {\ lambda _ {\ text {min } (D ^ {- 1} A) + \ lambda _ {\ text {max}} (D ^ {- 1} A)}} \ ،،}$

جایی که (kappa) $\ کاپا$ است تعداد شرط ماتریس .

منبع

https://en.wikipedia.org/wiki/Jacobi_method

روش گاوس-سییدل

توسط علی رضا نقش نیلچی | دوشنبه سی ام تیر ۱۳۹۹ | 13:16

از ویکیپدیا، دانشنامه آزاد

در جبر خطی عددی ، روش گاوس-سییدل ، همچنین به عنوان روش لیبمن یا روش جابجایی پی در پی شناخته می شود ، یک روش تکراری است که برای حل یک سیستم خطی از معادلات استفاده می شود . این نام به ریاضیدانان آلمانی کارل فردریش گاوس و فیلیپ لودویگ فون سییدل داده شده است و شبیه به روش ژاکوبی است . اگرچه می توان برای هر ماتریس با عناصر غیر صفر بر روی موربها اعمال شد ، همگرایی فقط در صورتی تضمین می شود که ماتریس به طور مورب به طور مسلط غالب باشد [1] ، یا متقارن و مثبت قطعی . این تنها در نامه ای خصوصی از گاوس به شاگردش گرلینگ در سال 1823 ذکر شده است. [2] انتشاراتی قبل از سال 1874 توسط Seidel ارائه نشده بود.

فهرست

توضیحات [ ویرایش ]

روش گاوس-سییدل یک روش تکراری برای حل سیستم مربعی معادلات خطی n با x ناشناخته است :

$A \ mathbf {x} = \ mathbf {b$ .

با تکرار تعریف می شود

$L _ {*} \ mathbf {x} ^ {(k + 1)} = \ mathbf {b} -U \ mathbf {x} ^ {(k)}،$

جایی که ) $\ mathbf {x} ^ {(k)$ است ک هفتم تقریب و یا تکرار $\ displaystyle \ mathbf {x}، \، \ mathbf {x} ^ {(k + 1)}$ تکرار بعدی یا k + 1 است $\ mathbf {x$ ، و ماتریس A به یک جزء مثلثی پایین تر تجزیه می شود $L _ {*$ ، و یک جزء کاملاً مثلثی فوقانی $A = L _ {*} + U$ . [3]

با جزئیات بیشتر ، A ، x و b را در اجزای آنها بنویسید :

سپس تجزیه A به مؤلفه مثلثی زیرین آن و جزء مثلثی فوقانی بالایی آن توسط:

$A = L _ {*} + U \ qquad {\ متن {جایی که}} \ qquad L _ {*} = {\ آغاز {bmatrix} a_ {11} & 0 & 0 cdots & 0 \\ a_ {21} & a_ {22} & \ cdots & 0 \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \ end {bmatrix}}، \ quad U = {\ آغاز {bmatrix} 0 & a_ {12} & \ cdots & a_ {1n \\ 0 & 0 & \ cdots & a_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & cdots & 0 \ end {bmatrix}.$

سیستم معادلات خطی ممکن است به صورت زیر بازنویسی شود:

$L _ {*} \ mathbf {x} = \ mathbf {b} -U \ mathbf {x$

روش گاوس-سییدل در حال حاضر با استفاده از مقدار قبلی x در سمت راست ، سمت چپ این عبارت را برای x حل می کند . از نظر تحلیلی ، این ممکن است به صورت زیر نوشته شود:

$\ mathbf {x} ^ {(k + 1)} = L _ {*} ^ {- 1} (\ mathbf {b} -U \ mathbf {x} ^ {(k)}).$

با این حال ، با استفاده از شکل مثلثی از $L _ {*$ عناصر (x ( k +1 را می توان با استفاده از تعویض رو به جلو محاسبه کرد :

$\ displaystyle x_ {i} ^ {(k + 1)} = {\ frac {1} {a_ {ii}} left \ سمت چپ (b_ {i} - \ sum _ {j = 1} ^ {i-1 } a_ {ij} x_ {j} ^ {(k + 1)} - \ sum _ {j = i + 1} ^ {n} a_ {ij} x_ {j} ^ {(k)} \ درست) ، \ quad i = 1،2 ، \ نقطه ، شماره}$ [4]

این روش به طور کلی ادامه می یابد تا تغییرات ایجاد شده در یک تکرار کمتر از تحمل مانند یک باقیمانده به اندازه کافی کوچک باشد.

بحث [ ویرایش ]

فرمول عاقلانه روش Gauss-Seidel بسیار شبیه به روش Jacobi است .

محاسبه (x ( k +1 از عناصر (x ( k +1 که قبلاً محاسبه شده اند استفاده می کند و فقط عناصر x ( k ) که در تکرار k + 1 محاسبه نشده اند ، استفاده می شود. این بدان معناست که برخلاف روش ژاکوبی ، فقط به عنوان یک وکتور ذخیره سازی لازم است زیرا عناصر را می توان در هنگام محاسبه رونویسی کرد ، که می تواند برای مشکلات بسیار بزرگ سودمند باشد.

اما برخلاف روش ژاکوبی ، محاسبات مربوط به هر عنصر به صورت موازی قابل انجام نیست . علاوه بر این ، مقادیر در هر تکرار به ترتیب معادلات اصلی بستگی دارد.

گاوس-سییدل همان SOR است (آرامش پی در پی بیش از حد) با $\ امگا = 1$ .

همگرایی [ ویرایش ]

خصوصیات همگرایی روش گاوس-سییدل به ماتریس A بستگی دارد . یعنی ، این روش در صورت وجود همگرا شناخته می شود:

A متقارن مثبت- قطعی است ، [5] یا
A کاملاً یا غیرقابل برگشت به صورت مورب مسلط است . [6]

روش گاوس-سییدل حتی اگر این شرایط راضی نباشد گاهی همگرا می شود.

الگوریتم [ ویرایش ]

از آنجا که عناصر را می توان رونویسی کرد زیرا در این الگوریتم محاسبه می شوند ، فقط به یک وکتور ذخیره سازی نیاز است و نمایه سازی بردار حذف می شود. الگوریتم به شرح زیر است:

ورودی: A ، b 
خروجی:

حدس اولیه را انتخاب کنید به محلول 
تکرار کنید تا همگرایی
     برای  I  از 1 تا  n  انجام ندهید

        برای  J  از 1 تا  N  انجام 
            اگر  J ≠ من  پس از آن

            در صورت 
        پایان ( پایان دادن به j )

    پایان ( من یکی از دایره)
    بررسی کنید که آیا همگرایی به دست آمده است یا خیر
پایان (تکرار)

مثالها [ ویرایش ]

نمونه ای از نسخه ماتریس [ ویرایش ]

یک سیستم خطی به عنوان نشان داده شده است $A \ mathbf {x} = \ mathbf {b$ از رابطه زیر بدست می آید:

$A = {\ شروع {bmatrix} 16 & 3 \\ 7 & -11 \\\ end {bmatrix}$ و آغاز $b = {\ fill bmatrix} 11 \\ 13 \ end {bmatrix}.$

ما می خواهیم از معادله استفاده کنیم

$\ mathbf {x} ^ {(k + 1)} = L _ {*} ^ {- 1} (\ mathbf {b} -U \ mathbf {x} ^ {(k)})$

در فرم

$\ mathbf {x} ^ {(k + 1)} = T \ mathbf {x} ^ {(k) + C$

جایی که:

$T = -L _ {*} ^ {- 1} U$ و $C = L _ {*} ^ {- 1} \ mathbf {b.$

ما باید تجزیه شویم $A _ {} ^ {}$ در مجموع یک جزء مثلثی پایین $L _ {*} ^ {}$ و یک جزء دقیق مثلثی فوقانی $U _ {} ^ {}$ :

$L _ {*} = {\ آغاز {bmatrix} 16 & 0 \\ 7 & -11 \\ end end {bmatrix$ $U = {\ شروع {bmatrix} 0 & 3 \\ 0 & 0 \ end {bmatrix}.$

معکوس از $L _ {*} ^ {}$ است:

$L _ {*} ^ {- 1} = {\ fill bmatrix} 16 & 0 \\ 7 & -11 \ end {bmatrix}} ^ {- 1} = {\ fill {bmatrix 0.0625 & 0.0000 \\ 0.0398 & -0.0909 \\\ end {bmatrix$ .

اکنون می توانیم پیدا کنیم:

$\ displaystyle T = - {\ fill bmatrix} 0.0625 & 0.0000 \\ 0.0398 & -0.0909 \ end {bmatrix}} \ بار \ fill bmatrix 0 & 3 \\ 0 & 0 \ end {bmatrix}} = {\ bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1194 \ end {bmatrix}} ،}$

$\ displaystyle C = {\ fill bmatrix} 0.0625 & 0.0000 \\ 0.0398 & -0.0909 \ end {bmatrix}} \ بار \ fill bmatrix 11 \\ 13 \ end {bmatrix}} = {\ آغاز bmatrix 68 0.6875 \\ - 0.7439 \ end {bmatrix}.$

حالا ما داریم $C _ {} ^ {}$ و ما می توانیم از آنها برای به دست آوردن بردارها استفاده کنیم $\ mathbf {x$ به طور تکراری

اول از همه ، ما باید انتخاب کنیم $\ mathbf {x} ^ {(0)$ : فقط می توان حدس زد. هرچه حدس بهتر باشد ، الگوریتم سریعتر عمل می کند.

ما فرض می کنیم:

$x ^ {(0) = {\ آغاز {bmatrix} 1.0 \\ 1.0 \ end {bmatrix}.$

سپس می توانیم محاسبه کنیم:

$x ^ {(1) = {\ آغاز {bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1193 \ end {bmatrix}} \ بار {\ fill {bmatrix 1.0 \\ 1.0 \ end {bmatrix}} + { \ fill bmatrix 68 0.6875 \ 0.6875 \\ - 0.7443 \ end {bmatrix}} = {\ fill bmatrix} 0.5000 \ - 0.8636 \ end {bmatrix.$

$x ^ {(2) = {\ fill bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1193 \ end {bmatrix}} \ بار {\ fill {bmatrix 0.5000 \\ - 0.8636 \ end {bmatrix}} + {\ fill bmatrix 68 0.6875 \\ - 0.7443 \ end {bmatrix} = {\ fill bmatrix} 0.8494 \\ - 0.6413 \ end {bmatrix}.$

$x ^ {(3) = {\ آغاز {bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1193 \ end {bmatrix}} \ بار {\ fill {bmatrix 0.8494 \ 0.8494 \\ - 0.6413 \\\ end {bmatrix } + {\ fill bmatrix} 0.6875 \\ - 0.7443 \ end {bmatrix}} = {\ fill bmatrix} 0.8077 \\ - 0.6678 \ end {bmatrix}.$

$x ^ {(4) = {\ آغاز {bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1193 \ end {bmatrix}} \ بار {\ fill {bmatrix 0.8077 \ 0.8077 \\ - 0.6678 \ end {bmatrix}} + {\ fill bmatrix 68 0.6875 \\ - 0.7443 \ end {bmatrix} = {\ fill bmatrix} 0.8127 \ \ - 0.6646 \ end {bmatrix}.$

$x ^ {(5) = {\ آغاز {bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1193 \ end {bmatrix}} \ بار {\ fill {bmatrix 0.8127 \ 0.8127 \\ - 0.6646 \ end {bmatrix}} + {\ fill bmatrix 68 0.6875 \\ - 0.7443 \ end {bmatrix} = {\ fill bmatrix} 0.8121 \\ - 0.6650 \ end bmatrix}.$

$x ^ {(6) = {\ آغاز {bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1193 \ end {bmatrix}} \ بار {\ fill {bmatrix 0.8121 \ 0.8121 \\ - 0.6650 \ end {bmatrix}} + {\ fill bmatrix 68 0.6875 \\ - 0.7443 \ end {bmatrix} = {\ fill bmatrix} 0.8122 \\ - 0.6650 \ end {bmatrix}.$

$x ^ {(7) = {\ آغاز {bmatrix} 0.000 & -0.1875 \\ 0.000 & -0.1193 \ end {bmatrix}} \ بار {\ fill bmatrix 0.8122 \ 0.8122 \\ - 0.6650 \ end {bmatrix}} + {\ fill bmatrix 68 0.6875 \\ - 0.7443 \ end {bmatrix} = {\ fill bmatrix} 0.8122 \\ - 0.6650 \ end {bmatrix}.$

همانطور که انتظار می رود ، الگوریتم به راه حل دقیق همگرا می شود:

$\ displaystyle \ mathbf {x} = A ^ {- 1} \ mathbf {b} \ تقریبی {\ آغاز {bmatrix} 0.8122 \\ - 0.6650 \ end {bmatrix}}.$

در حقیقت ، ماتریس A کاملاً مورب مسلط است (اما قطعی مثبت نیست).

مثال دیگر برای نسخه ماتریس [ ویرایش ]

سیستم خطی دیگری که به عنوان نشان داده شده است $A \ mathbf {x} = \ mathbf {b$ از رابطه زیر بدست می آید:

$A = {\ شروع {bmatrix 2 & 3 \\ 5 & 7 \\ end {bmatrix}$ و $b = {\ شروع {bmatrix} 11 \\ 13 \\\ end {bmatrix.$

ما می خواهیم از معادله استفاده کنیم

$\ mathbf {x} ^ {(k + 1)} = L _ {*} ^ {- 1} (\ mathbf {b} -U \ mathbf {x} ^ {(k)})$

در فرم

$\ mathbf {x} ^ {(k + 1)} = T \ mathbf {x} ^ {(k) + C$

جایی که:

$T = -L _ {*} ^ {- 1} U$ و $C = L _ {*} ^ {- 1} \ mathbf {b.$

ما باید تجزیه شویم $A _ {} ^ {}$ در مجموع یک جزء مثلثی پایین $L _ {*} ^ {}$ و یک جزء دقیق مثلثی فوقانی $U _ {} ^ {}$ :

$L _ {*} = {\ شروع {bmatrix 2 & 0 \\ 5 & 7 \\ end {bmatrix$ و $U = {\ شروع {bmatrix} 0 & 3 \\ 0 & 0 \\ end {bmatrix}.$

معکوس از $L _ {*} ^ {}$ است:

$L _ {*} ^ {- 1} = {\ fill {bmatrix} 2 & 0 \\ 5 & 7 \** end {bmatrix}} ^ {- 1} = {\ fill bmatrix} 0.500 & 0.000 \\ - 0.357 & 0. 143 \\\ end {bmatrix}$ .

اکنون می توانیم پیدا کنیم:

$T = - {\ fill bmatrix} 0.500 & 0.000 \\ - 0.357 & 0.143 \\\ end {bmatrix} \ بار {\ آغاز {bmatrix 0 & 3 \\ 0 & 0 \ end end {bmatrix}} = { \ fill bmatrix 000 0.000 & -1.500 \ 0.000 & 1.071 \\\ end {bmatrix}} ،$

$C = {\ fill bmatrix} 0.500 & 0.000 \\ - 0.357 & 0.143 \\\ end {bmatrix} \ بار {\ آغاز {bmatrix 11 \\ 13 \\ end {bmatrix}} = {\ شروع {bmatrix 5 5.500 \ 5.500 \ - 2.071 \\\ end {bmatrix.$

حالا ما داریم $T _ {} ^ {}$ و $C _ {} ^ {}$ و ما می توانیم از آنها برای به دست آوردن بردارها استفاده کنیم $\ mathbf {x$ به طور تکراری

اول از همه ، ما باید انتخاب کنیم $\ mathbf {x} ^ {(0)$ : فقط می توان حدس زد. هرچه حدس بهتر باشد ، الگوریتم سریعتر انجام می شود.

ما فرض می کنیم:

$x ^ {(0) = {\ آغاز {bmatrix} 1.1 \\ 2.3 \\\ end {bmatrix.$

سپس می توانیم محاسبه کنیم:

$x ^ {(1) = {\ آغاز {bmatrix} 0 & -1.500 \\ 0 & 1.071 \\\ end {bmatrix} \ times \ fill bmatrix} 1.1 \\ 2.3 \\ end {bmatrix} + {\ fill bmatrix} 5.500 \ - 2.071 \\\ end {bmatrix}} = {\ fill bmatrix} 2.050 \\ 0.393 \\\ end {bmatrix}.$

$x ^ {(2) = {\ fill bmatrix} 0 & -1.500 \\ 0 & 1.071 \\\ end {bmatrix} \ times \ fill bmatrix} 2.050 \\ 0.393 \\\ end {bmatrix} + {\ fill bmatrix} 5.500 \ - 2.071 \\\ end {bmatrix}} = {\ fill bmatrix} 4.911 \ - 1.651 \\\ end {bmatrix}.$

$x ^ {(3)} = \ cdots. \،$

اگر ما برای همگرایی تست کنیم ، متوجه می شویم که این الگوریتم متفاوت است. در واقع ، ماتریس A نه به طور مورب مسلط است و نه قطعی مثبت. سپس ، همگرایی به راه حل دقیق

$\ mathbf {x} = A ^ {- 1} \ mathbf {b} = {\ آغاز {bmatrix -38 \\ 29 \ end {bmatrix}$

تضمین شده نیست و در این حالت رخ نخواهد داد.

نمونه ای از نسخه معادله [ ویرایش ]

فرض کنید معادلات k داده شده در جایی که x n بردارهای این معادلات و نقطه شروع x 0 هستند . از اولین معادله برای x 1 از نظر $x_ {n + 1} ، x_ {n + 2} ، \ dot، x_ {n.$ برای معادلات بعدی مقادیر قبلی x s را جایگزین کنید .

برای روشن شدن آن یک نمونه را در نظر بگیرید.

$\ displaystyle \ fill {array} {rrrrl} 10x_ {1} & - x_ {2} & + 2x_ {3} && = 6، \\ - x_ {1} & + 11x_ {2} & - x_ {3 } & + 3x_ {4} & = 25، \\ 2x_ {1} & - x_ {2} & + 10x_ {3} & - x_ {4} & = - 11، \\ & 3x_ {2} & - x_ 3} & + 8x_ {4} & = 15. \ end {array}}$

حل کردن برای $x_ {1} ، x_ {2} ، x_ {3$ و $x_ {4$ می دهد:

${\ شروع {تراز شده} x_ {1} & = x_ {2} / 10-x_ {3} / 5 + 3/5، \\ x_ {2} & = x_ {1} / 11 + x_ {3} / 11-3x_ {4} / 11 + 25/11، \\ x_ {3} & = - x_ {1} / 5 + x_ {2} / 10 + x_ {4} / 10-11 / 10، \\ x_ {4} & = - 3x_ {2} / 8 + x_ {3} /8+15/8.\end {تراز شده}}$

فرض کنید ما (0 ، 0 ، 0 ، 0) را به عنوان تقریب اولیه انتخاب می کنیم ، سپس اولین راه حل تقریبی توسط

${\ شروع {تراز شده} x_ {1} & = 3/5 = 0.6 ، \\ x_ {2} & = (3/5) /11+25/11=3/55+25/11=2.3272 ، \\ x_ {3} & = - (3/5) / 5 + (2.3272) /10-11/10=-3/25+0.23272-1.1=-0.9873، \\ x_ {4} & = - 3 (2.3272) /8+(-0.9873)/8+15/8=0.8789.\end{aligned}}$

با استفاده از تقریبهای به دست آمده ، روش تکراری تا رسیدن به دقت مطلوب تکرار می شود. در زیر راه حل تقریبی بعد از چهار تکرار است.

$\ displaystyle \ fill {array} {llll} x_ {1} & x_ {2} & x_ {3} & x_ {4} \\\ hline 0.6 & 2.32727 & -0.987273 & 0.878864 \\ 1.03018 & 2.03694 & -1.01446 & 0 .984341 \\ 1.00659 & 2.00356 & -1.00253 & 0.998351 \\ 1.00086 & 2.0003 & -1.00031 & 0.99985 \ end {array}}}$

راه حل دقیق سیستم (1 ، 2 ، −1 ، 1) است .

مثالی با استفاده از Python و NumPy [ ویرایش ]

روش عددی زیر به سادگی برای تولید بردار راه حل تکرار می کند.

واردات  numpy  به عنوان  np

ITERATION_LIMIT  =  1000

# مقدار اولیه ماتریس 
A  =  np . آرایه ([[ 10. ،  - 1. ،  2. ،  0. ]، 
              [ - 1. ،  11. ،  - 1. ،  3. ]، 
              [ 2. ،  - 1. ،  10. ،  - 1. ]، 
              [ 0. ،  3. ،  - 1. ،  8. ]]) 
# بردار RHS 
b  =  np را اولیه کنید . آرایه ([6. ،  25. ،  - 11. ،  15. ])

چاپ ( "سیستم معادلات:" ) 
برای  من  در  دامنه ( . شکل [ 0 ]): ردیف = [ " {0: 3G} * X {1} " . فرمت ( [ من ، J ]، J + 1 ) برای J در دامنه ( . شکل [ 1 ])] چاپ ( "[ {0} ] = [ {1: 3G} ]" .
              
    قالب ( "+" . پیوستن به ( ردیف ) ،  b [ i ]))

x  =  np . zeros_like ( b ) 
برای  it_count  در  دامنه ( 1 ،  ITERATION_LIMIT ): 
    x_new  =  np . zeros_like ( X ) 
    چاپ ( "تکرار {0} : {1} " . فرمت ( it_count ،  X )) 
    برای  من  در  دامنه ( . شکل [ 0 ]): S1 = NP .
          نقطه ( [ من ، : من ]، x_new [: من ]) S2 = NP . dot ( A [ i ، i + 1 :]، x [ i + 1 :]) x_new [ i ] = ( b [ i ] - s1 - s2 ) / A [ i ، i ] اگر np . تمیز کردن  
                
                 
     ( x ،  x_new ،  rtol = 1e-8 ): 
        break 
    x  =  x_new

چاپ ( "راه حل: {0} " . فرمت ( x )) 
خطا  =  np . نقطه ( ، X ) - ب چاپ ( "خطا: {0} " . فرمت ( خطا ))

خروجی را تولید می کند:

سیستم  از  معادلات : 
[  10 * X1  +   - 1 * X2  +    2 * X3  +    0 * X4 ]  =  [   6 ] 
[  - 1 * X1  +   11 * X2  +   - 1 * X3  +    3 * X4 ]  =  [  25 ] 
[   2 * x1  +   - 1 * x2  +  10 * x3  +   - 1 * x4 ]  =  [ - 11 ] 
[   0 * x1  +    3 * x2  +   - 1 * x3  +    8 * x4 ]  =  [  15 ] 
Iteration  1 :  [  0.   0.   0.   0. 0. ] 
Iteration  2 :  [  0.6          2.32727273  - 0.98727273   0.87886364 ] 
تکرار 3 :  [  1.03018182   2.03693802  - 1.0144562    0.98434122 ] 
تکرار  4 :  [  1.00658504   2.00355502  - 1.00252738   0.99835095 ] 
تکرار  5 :  [  1.00086098   2.00029825  - 1.00030728   0.99984975 ] 
تکرار  6 :  [  1.00009128   2.00002134  - 1.00003115   0.9999881  ] 
تکرار  7 :  [  1.00000836   2.00000117  - 1.00000275  0.99999922 ] 
تکرار  8 :  [  1.00000067   2.00000002  - 1.00000021   0.99999996 ] 
تکرار  9 :  [  1.00000004   1.99999999  - 1.00000001   1.         ] 
تکرار  10 :  [  1.   2.  - 1.   1. ] 
راه حل :  [  1.   2.  - 1.   1. ] 
خطا :  [   2.06480930e-08   - 1.25551054e-08    3.61417563e-11    0.00000000e + 00]

برنامه ای برای حل خودسرانه شماره. معادلات با استفاده از Matlab [ ویرایش ]

$x_ {i} ^ {(k + 1)} = {\ frac {1} {a_ {ii}}} \ سمت چپ (b_ {i} - \ sum _ {j <i} a_ {ij} x_ {j} ^ {(k + 1) - \ sum _ {j> i} a_ {ij} x_ {j} ^ {(k)} \ Right)، \ quad i، j = 1،2، \ ldots، n$

تابع  x = gauss_seidel ( A ، b ، X ، iters ) 
    برای  i  =  1 : iters 
        برای j = 1: size (A، 1)
            x ( j )  =  ( 1 / A ( j ، j ))  *  ( b ( j )  -  A ( j ، :) * x  +  A ( j ، j ) * x ( j ))؛
        پایان 
پایان    
پایان

منبع

https://en.wikipedia.org/wiki/Gauss%E2%80%93Seidel_method

تبدیل ویل

توسط علی رضا نقش نیلچی | دوشنبه سی ام تیر ۱۳۹۹ | 2:20

کمیت تغییر شکل [ ویرایش ]

بصری ، تغییر شکل یک شیء ریاضی ، خانواده ای از همان نوع اشیاء است که به پارامترهای مختلفی بستگی دارد. در اینجا ، قوانینی برای چگونگی تغییر شکل دادن به جبر تبانی "کلاسیک" از مشاهدات به یک جبر کوانتومی غیر قابل تغییر از مشاهدات فراهم می کند.

طرح اصلی در تئوری تغییر شکل ، شروع با یک ساختار جبری است (مثلاً یک جبر دروغ بگویید ) و بپرسید: آیا یک یا چند پارامتر (خانواده) از ساختارهای مشابه وجود دارد ، به طوری که برای یک مقدار اولیه پارامتر (ها) یکی با همین ساختار (دروغ دروغ) یکی با آن شروع شده است؟ (قدیمی ترین نمونه این ممکن است تحقق Eratosthenes در جهان باستان باشد که یک زمین مسطح از یک کره کروی تغییر شکل پذیر است ، با پارامتر تغییر شکل 1 / R ⊕ .) به عنوان مثال ، ممکن است یک torus noncommutative را به عنوان کمیت تغییر شکل از طریق ★محصول را به طور ضمنی به همه ظرافت های همگرایی (که معمولاً در کمیت تغییر شکل رسمی مورد توجه قرار نمی گیرند) بپردازید. با توجه به اینکه جبر توابع موجود در یک فضا هندسه آن فضا را تعیین می کند ، مطالعه محصول ستاره منجر به مطالعه تغییر شکل هندسه غیرتهاجمی آن فضا می شود.

در زمینه بالا تخت به عنوان مثال فاز فضا، محصول ستاره ( کالا مویال ، در واقع توسط Groenewold در سال 1946 معرفی)، ★ Ħ ، از یک جفت از توابع در F 1 ، F 2 ∈ C ∞ (ℜ 2 ) است، مشخص شده توسط

$\ Phi [f_1 \ star f_2] = \ Phi [f_1] \ Phi [f_2]. \،$

محصول ستاره به طور کلی قابل تعویض نیست ، اما در حد 0 comm comm به محصول رفتاری معمولی می رود . به این ترتیب ، گفته می شود که تغییر شکل جبر رفتاری C ∞ ( 2 ℜ ) را تعریف می کند .

برای مثال Weyl-map بالا ، محصول ★ ممکن است از نظر قلم پواسون نوشته شود

$f_1 \ star f_2 = \ sum_ {n = 0} ^ \ infty \ frac {1} {n!} \ left (\ frac {i \ hbar} {2} \ Right) ^ n \ Pi ^ n (f_1، f_2 )$

در اینجا ، پی بوستون Poisson است ، اپراتوری به گونه ای تعریف شده است که قدرت آن باشد

$\ Pi ^ 0 (f_1 ، f_2) = f_1f_2$

$\ Pi ^ 1 (f_1، f_2) = \ {f_1، f_2 \} = \ frac {\ partial f_1} {\ part q q} \ frac {\ partial f_2} {\ جزئی p} - \ frac {\ جزئی f_1} {\ جزئی جزئی} \ frac {\ جزئی f_2} {\ جزئی q} ~ ،$

که در آن { F 1 ، F 2 } است براکت پواسون . به طور کلی،

$\ Pi ^ n (f_1، f_2) = \ sum_ {k = 0} ^ n (-1) ^ k {n \ انتخاب k} \ چپ (\ frac {\ جزئی) ^ k} {\ جزئی p ^ k} \ frac {\ جزئی ^ {nk}} {\ جزئی q ^ {nk}} f_1 \ راست) \ بار \ چپ (\ frac {\ جزئی) ^ ^ nk}} {\ جزئی p ^ {nk}} \ frac {\ جزئی ^ k} {\ جزئی q ^ k} f_2 \ درست)$

جایی که را انتخاب کنید} ${n \ k انتخاب کنید$ است ضریب دو جمله ای .

بنابراین ، به عنوان مثال ، [8] گاوسی ها به صورت ابرقابل بیان ،

$\ exp \ left (- {a} (q ^ 2 + p ^ 2) \ Right) ~ \ star \ exp \ left (- {b} (q ^ 2 + p ^ 2) \ Right) = {1 \ بیش از 1+ \ hbar ^ 2 ab} \ exp \ left (- {a + b \ over 1+ \ hbar ^ 2 ab} (q ^ 2 + p ^ 2) \ Right)،$

یا

$\ delta (q) ~ \ star ~ \ delta (p) = {2 \ h h} \ exp \ left (2i {qp \ over \ hbar} \ right)،$

غیره. این فرمول ها در مختصاتی که در آن شاخه پواسون ثابت است (براکت های ساده و صاف پواسون) پیش بینی شده است. برای فرمول کلی در منیفولدهای پواسون دلخواه ، به شماره فرمول تدریج Kontsevich .

Antisymmetrization این ★ بازده -product براکت مویال ، تغییر شکل کوانتومی مناسب از براکت پواسون ، و همشکل فاز فضا (ویگنر تبدیل) از کوانتومی کموتاتور در حد معمول بیشتر فرمول هیلبرت-فضای از مکانیک کوانتومی. به همین ترتیب ، آن را سنگ بنای معادلات دینامیکی رصدها در این فرمول فاز فضا قرار می دهد.

نتایج حاصل از فرمولاسیون کامل فاز مکانیک کوانتومی ، کاملاً معادل نمایندگی اپراتور فضایی هیلبرت ، با اپراتور موازی ضربات چند برابر با ضریب همبستگی ستاره ای است. [8]

مقدار چشمداشتی در کوانتیزه فاز فضا isomorphically به ردیابی اپراتور مشاهدات به دست آمده Φ با ماتریس چگالی در فضای هیلبرت: آنها با انتگرال فاز فضای مشاهدات به دست آمده مانند بالا F با ویگنر توزیع شبه احتمال موثر در خدمت به عنوان یک اقدام .

بنابراین ، با بیان مکانیک کوانتومی در فضای فاز (همان تردد مکانیک کلاسیک) ، نقشه فوق Weyl شناخت مکانیک کوانتومی را به عنوان تغییر شکل (عمومی سازی ، اصل مکاتبات Cf. ) مکانیک کلاسیک ، با پارامتر تغییر شکل ħ / S تسهیل می کند . (سایر تغییر شکلهای آشنا در فیزیک شامل تغییر شکل نیوتن کلاسیک به مکانیک نسبیت گرایانه ، با پارامتر تغییر شکل V / c ؛ یا تغییر شکل گرانش نیوتنی به نسبیت عام ، با پارامتر تغییر شکل شوارتزیلد - شعاع / بعد-ویژگی) در مقابل ، انقباض گروه منجر می شود. پارامترهای ناپدید شده نظریه های کلاسیک را تغییر شکل نداد.)

عبارت کلاسیک، مشاهدات، و عملیات (مانند براکت پواسون) بر اساس اصلاح Ħ اصلاحات کوانتومی وابسته، به عنوان ضرب خاصیت جابجایی معمولی استفاده در مکانیک کلاسیک به تعمیم غیر مبادلهای ستاره ضرب توصیف مکانیک کوانتومی و اساسی اصل عدم قطعیت آن است.

با وجود نام آن ، Quantization Deformation یک طرح سنجش موفقیت آمیز نیست ، یعنی روشی برای تولید یک تئوری کوانتومی از یک روش کلاسیک. این فقط یک تغییر نمایندگی از فضای هیلبرت به فضا فضا است.

مقاله اصلی: فرمول بندی فاز فضا

کلیات [ ویرایش ]

در کلیت بیشتر ، کمیت ویل در مواردی مورد مطالعه قرار می گیرد که فضای فاز یک مانیفولد دلسوز یا احتمالاً منیفولد پواسون باشد . ساختارهای مرتبط شامل گروههای Poisson-Lie و جبرهای Kac-Moody است .

منبع

https://en.wikipedia.org/wiki/Wigner%E2%80%93Weyl_transform

تبدیل ویل

توسط علی رضا نقش نیلچی | دوشنبه سی ام تیر ۱۳۹۹ | 2:19

فرمول اساسی [ ویرایش ]

ویل تبدیل (یا تدریج ویل ) از تابع f را توسط اپراتور زیر در فضای هیلبرت داده می شود،

$\ displaystyle \ Phi [f] = {\ frac {1} {(2 \ pi) ^ {2}}} \ iint \! \! \! \ iint f (q، p) \ left (e ^ {i (a (Qq) + b (Pp))} \ right) {\ text {d}} q \، {\ text {d}} p \، {\ text d}} a \، {\ text {d } ب.$

در طول ، $\ hbar$ است ثابت کاهیده پلانک .

انجام انتگرال های p و q ابتدا در فرمول فوق آموزنده است که اثر محاسبات تبدیل فوریه معمولی را دارد. ${\ tilde {f}$ از عملکرد $f$ ، در حالی که اپراتور را ترک می کنید

$\ displaystyle e ^ {i (aQ + bP)}$ . در این حالت ، تبدیل Weyl می تواند به صورت [5] نوشته شود .

$\ displaystyle \ Phi [f] = {\ frac {1} {(2 \ pi) ^ {2}}} \ iint {\ tilde {f}} (a، b) e ^ iaQ + ibP} \، دا ، db$ .

بنابراین ممکن است ما از نقشه Weyl به شرح زیر فکر کنیم: ما یک تبدیل معمولی فوریه از عملکرد را می گیریم ) $f (p ، q)$ اما پس از اعمال فرمول وارونگی فوریه ، عملگرهای کوانتومی را جایگزین می کنیم $پ$ و $س$ برای متغیرهای اصلی کلاسیک $پ$ و $ق$ بنابراین ، یک نسخه کوانتومی از {\ displaystyle f $f$ ""

شکل کمتر متقارن ، اما مفید برای برنامه های کاربردی ، به شرح زیر است:

$\ displaystyle \ Phi [f] = {\ frac {2} {(2 \ pi \ hbar) ^ {3/2}}} \ iint \! \! \! \ iint \! \! dqdpd {\ tilde { x}} d {\ tilde {p}} ~ e ^ {{\ frac {i} {\ hbar}} ({\ tilde {x}} {\ tilde {p}} - 2 ({\ tilde {p -p) ({\ tilde {x}} - q))} ~ f (q، p) ~ | {\ tilde {x}} \ rangle \ langle {\ tilde {p} | |}$

در نمایه موقعیت [ ویرایش ]

نقشه Weyl سپس ممکن است از نظر عناصر ماتریس هسته انتگرال این اپراتور بیان شود ، [6]

$\ langle x | \ Phi [f] | y \ rangle = \ int _ {- \ infty} ^ \ infty {\ text {d} p \ over h} ~ e ^ {ip (xy) / \ hbar} ~ f \ left ({x + y \ over2 ، p \ درست).$

نقشه معکوس [ ویرایش ]

معکوس از بالا نقشه ویل است نقشه ویگنر ، که طول می کشد اپراتور Φ بازگشت به اصل فاز- فضا تابع هسته F ،

$f (q، p) = 2 \ int _ {- \ infty} ^ \ infty \ text {d} y ~ e ^ {- 2ipy / \ hbar} ~ \ langle q + y | \ Phi [f] | qy \ rangle.$

اگر کسی جایگزین شود $\ displaystyle \ Phi [f]$ در عبارت بالا با اپراتور دلخواه، تابع نتیجه F در ثابت پلانک بستگی دارد Ħ ، و ممکن است به خوبی توصیف فرآیندهای مکانیک کوانتومی، به شرط آن است که به درستی از طریق تشکیل محصول ستاره ، در زیر. [7] به نوبه خود ، نقشه Weyl از نقشه Wigner با فرمول گرونew ولد خلاصه می شود ، [8]

$\ displaystyle \ Phi [f] = h \ iint \، da \، db ~ e ^ {iaQ + ibP \ operatorname {Tr} (e ^ {- iaQ-ibP} \ Phi).$

کمیت Weyl از مشاهدات چند جمله ای [ ویرایش ]

در حالی که فرمولهای بالا درک خوبی از کمی سازی Weyl از یک مشاهده بسیار کلی در فضای فاز دارند ، آنها برای محاسبات بر روی مشاهدات ساده ، مانند مواردی که چند جمله ای در آن هستند ، بسیار مناسب نیستند. $ق$ و $پ$ . در بخش های بعدی خواهیم دید که در چنین چند جمله ای ها ، کمیت Weyl نشان دهنده ترتیب کاملاً متقارن از اپراتورهای غیرموتور است. $س$ و $پ$ . به عنوان مثال، نقشه ویگنر از کوانتومی زاویه ای-حرکت مربع اپراتور L 2 است که فقط حرکت زاویه ای کلاسیک مربع نیست، اما آن را بیشتر شامل مدت جبران -3 Ħ 2 /2 ، که حساب برای حرکت زاویه ای nonvanishing از زمین سولید استیت مدار بور .

خواص [ ویرایش ]

کمیت Weyl از چندجملهای [ ویرایش ]

عمل اندازه گیری Weyl در توابع چند جمله ای $ق$ و $پ$ کاملاً با فرمول متقارن زیر مشخص می شود: [9]

$\ displaystyle (aq + bp) ^ {n} \ longmapsto (aQ + bP) ^ {n}$

برای همه اعداد واقعی $آ$ و $ب$ . از این فرمول ، نشان دادن کمیت ویل بر عملکردی از فرم دشوار نیست $\ displaystyle q ^ {k} p ^ {l}$ میانگین کل سفارشات ممکن را می دهد $ک$ عوامل $س$ و $ل$ عوامل $پ$ . مثلاً ما داریم

$\ displaystyle 6p ^ {2} q ^ {2} ~~ \ longmapsto ~~ P ^ {2} Q ^ {2} + Q ^ {2} P ^ {2} + PQPQ + PQ ^ {2} P + QPQP + QP ^ {2} Q.$

اگرچه این نتیجه از نظر مفهومی طبیعی است ، اما برای محاسبات زمانی مناسب نیست $ک$ و $ل$ بزرگ هستند در چنین مواردی ، ما می توانیم به جای فرمول McCoy استفاده کنیم [10]

$\ displaystyle p ^ {m} q ^ {n} ~~ \ longmapsto ~~ {1 \ over 2 ^ {n}} \ sum _ {r = 0} ^ {n} {n \ انتخاب r} Q ^ { r} P ^ {m} Q ^ {nr} = {1 \ over 2 ^ {m}} \ sum _ {s = 0} ^ {m} {m \ انتخاب s} P ^ {s} Q ^ {n } P ^ {ms}.$

این عبارت یک پاسخ ظاهراً متفاوت برای پرونده $\ displaystyle p ^ {2} q ^ {2}$ از بیان کاملاً متقارن در بالا. با این وجود هیچ تضادی وجود ندارد ، از آنجا که روابط رفت و برگشت کانونی بیش از یک عبارت را برای همان اپراتور مجاز می کند. (خواننده ممکن است استفاده از روابط رفت و آمد را برای بازنویسی فرمول کاملاً متقارن برای پرونده مفید باشد. $\ displaystyle p ^ {2} q ^ {2}$ از نظر اپراتورها $Q \ displaystyle QP ^ {2} Q}$ و $\ displaystyle Q ^ {2} P ^ {2}$ و اولین بیان را در فرمول مک کوی با $\ displaystyle m = n = 2$ .)

به طور گسترده ای تصور می شود که اندازه گیری ویل ، از بین تمام طرح های سنجش کمترین حد ممکن ، به نقشه برداری براکت پواسون در سمت کلاسیک به رفت و آمد در سمت کوانتومی نزدیک می شود. (مکاتبات دقیق با توجه به قضیه گرونewولد غیرممکن است .) برای مثال ، [11]

قضیه : اگر ${\ نمایشگر f (q ، p)$ چند جمله ای درجه حداکثر 2 و ${\ نمایشگر g (q ، p)$ پس از آن ما چند جمله ای خودسرانه داریم

$\ displaystyle \ Phi (\ {f، g \}) = {\ frac {1} {i \ hbar}} [\ Phi (f)، \ Phi (g)]}$ .

کمیت ویل از توابع کلی [ ویرایش ]

اگر F است تابع حقیقی ، سپس ویل نقشه تصویر خود را Φ [ F ] است خود الحاقی .
اگر F یک عنصر از است فضای شوارتز ، پس از آن Φ [ F ] است طبقه اثری .
به طور کلی ، Φ [ f ] یک اپراتور بدون مرز متراکم تعریف شده است .
نقشه Φ [ f ] از یک به یک در فضای شوارتز (به عنوان یک فضای فرعی از توابع مربع یکپارچه) است.

منبع

https://en.wikipedia.org/wiki/Wigner%E2%80%93Weyl_transform

تبدیل ویل - وینگر

توسط علی رضا نقش نیلچی | دوشنبه سی ام تیر ۱۳۹۹ | 2:12

تبدیل Wigner-Weylدر مکانیک کوانتومی ، تبدیل ویل - وینگر یا ویل - وینگر (پس از هرمان Weyl و یوجین Wigner ) یک نقشه برداری معکوس بین توابع در فرمول فضای فاز کوانتومی و اپراتورهای فضای هیلبرت در تصویر شرودینگر است .

معمولاً نقشه برداری از توابع در فاز فاز به اپراتورها تبدیل ویل یا کمیت ویل گفته می شود ، در حالی که نقشه برعکس ، از اپراتورها تا توابع در فضای فاز ، Wigner transform نامیده می شود . این نقشه برداری ابتدا در سال 1927 توسط هرمان ویل در تلاش برای نقشه برداری از توابع فاز کلاسیک تقارن شده برای اپراتورها ابداع شد ، روشی که به کمیت سازی ویل معروف است . [1] اکنون فهمیده شده است که کمیت ویل همه خصوصیاتی را که برای تعیین کمیت لازم است را برآورده نمی کند و بنابراین گاهی اوقات پاسخ های غیرفیزیکی می دهد. از طرف دیگر ، برخی از ویژگیهای خوب که در زیر توضیح داده شده نشان می دهد که اگر فردی به دنبال توابع نقشه برداری روش ثابت اندازه گیری منفرد در فضای فاز کلاسیک برای اپراتورها باشد ، کمیت ویل بهترین گزینه است. ( قضیه گرونew ولد می گوید که هیچ نقشه ای نمی تواند تمام خصوصیاتی را که ایده آل می باشد داشته باشد.)

صرف نظر از این ، تبدیل ویل - وینگر یک تحول انتگرالی کاملاً تعریف شده بین بازه فاز و بازنماییهای اپراتور است و بینشی در عملکرد مکانیک کوانتومی دارد. از همه مهمتر ، توزیع شبه احتمال Wigner تبدیل Wigner از ماتریس چگالی کوانتومی استو برعکس ، ماتریس چگالی تبدیل ویل از عملکرد Wigner است. برخلاف اهداف اصلی ویل در جستجوی یک طرح کمیت سنجی مداوم ، این نقشه صرفاً به تغییر نمایندگی در مکانیک کوانتومی مربوط می شود. نیازی به اتصال "کلاسیک" با مقادیر "کوانتومی" نیست. به عنوان مثال ، عملکرد فاز فضا ممکن است صریحاً به ثابت anc پلانک بستگی داشته باشد ، همانطور که در برخی موارد آشنا با حرکت زاویه ای انجام می شود. این تغییر نمایندگی برگشت ناپذیر سپس به فرد امکان می دهد مکانیک کوانتومی را در فضای فاز بیان کند ، همانطور که در دهه 1940 توسط هیلبراند جی. گرونewولد [2] و خوزه انریکه وفادار مورد قدردانی قرار گرفت . [3] [4]

فهرست

تعریف کمیت ویل از یک مشاهده کلی [ ویرایش ]

در زیر تحول ویل در ساده ترین ، فاز دو مرحله ای اقلیدسی توضیح داده شده است. بگذارید مختصات موجود در فضای فاز (q ، p) باشند و بگذارید f یک تابعی باشد که در همه جا در فضای فاز تعریف شده است. در آنچه در زیر می آید ، ما عملگرهای P و Q را برآورده می کنیم که روابط رفت و برگشتی متعارف مانند عملکرد معمولی موقعیت و حرکت در نمایندگی شرودینگر را برآورده می کنند . ما فرض می کنیم که اپراتورهای نمایی $\ displaystyle e ^ {iaQ}}$ و $\ displaystyle e ^ {ibP}}$ نمایشی غیرقابل برگشت از روابط ویل را تشکیل می دهند ، به گونه ای که قضیه استون فون نویمان (تضمین یگانگی روابط رفت و آمد متعارف).

منبع

https://en.wikipedia.org/wiki/Wigner%E2%80%93Weyl_transform

مقیاس های ویل

توسط علی رضا نقش نیلچی | دوشنبه سی ام تیر ۱۳۹۹ | 2:0

ویل اسکارال

در فرمالیسم Newman-Penrose (NP) از نسبیت عام ، مقیاس های ویل به مجموعه ای از پنج مقیاس پیچیده اشاره دارند $\ {\ Psi _ {0} ، \ Psi _ {1}، \ Psi _ {2}، \ Psi _ {3}، \ Psi _ {4} \}$ که ده مؤلفه مستقل از تانسور Weyl از یک فضا زمان چهار بعدی را رمزگذاری می کند .

فهرست

تعاریف [ ویرایش ]

با توجه به یک تتراد پیچیده تهی $\ {l ^ {a} ، n ^ {a} ، m ^ {a} ، {\ bar {m}} ^ {a} \}$ و با همایش $\ {(- ، + ، + ، +)؛ l ^ a n_a = -1 \، m ^ a \ bar {m} _a = 1 \$ مقیاسهای Weyl-NP توسط [1] [2] [3] تعریف شده اند

$\ Psi _ {0}: = C _ {{\ alpha \ beta \ gamma \ delta}} l ^ {\ alpha} m ^ {\ beta} l ^ {\ gamma} m ^ {\ delta} \،$

$\ Psi _ {1}: = C _ {{\ alpha \ beta \ gamma \ delta}} l ^ {\ alpha} n ^ {\ beta} l ^ {\ gamma} m ^ {\ delta} \،$

$\ Psi _ {2}: = C _ {{\ alpha \ beta \ gamma \ delta}} l ^ {\ alpha} m ^ {\ beta} {\ bar {m}} ^ {\ gamma} n ^ {\ delta } \ ،$

$\ Psi _ {3}: = C _ {{\ alpha \ beta \ gamma \ delta}} l ^ {\ alpha} n ^ {\ beta} {\ bar {m}} ^ {\ gamma} n ^ {\ delta } \ ،$

$\ Psi _ {4}: = C _ {{\ alpha \ beta \ gamma \ delta}} n ^ {\ alpha} {\ bar {m}} ^ {\ beta} n ^ {\ gamma} {\ bar {m } ^ {\ دلتا} \.$

نکته: اگر کسی کنوانسیون را اتخاذ کند $\ {(+ ، - ، - ، -)؛ l ^ a n_a = 1 \، m ^ a \ bar {m} _a = -1 \$ تعاریف $\ Psi_i$ باید مقادیر متضاد را بدست آورد. [4] [5] [6] [7] یعنی

$\ Psi _ {i} \ mapsto - \ Psi _ {i}$ بعد از انتقال امضا

مشتقات جایگزین [ ویرایش ]

همچنین ببینید: معادلات میدان نیومن - پنروز

با توجه به تعاریف فوق ، قبل از محاسبه مقیاس های Weyl-NP از طریق انقباض با بردارهای تتراد مربوطه ، باید از تنورهای Weyl پی برد. با این حال ، این روش به طور کامل روحیه فرمالیسم نیومن-پنروز را نشان نمی دهد . به عنوان جایگزین، یک ابتدا می تواند محاسبه ضرایب چرخش و سپس با استفاده از معادلات میدان NP به استخراج پنج ویل-NP بندی [ نیازمند منبع ]

$\ Psi _ {0} = D \ sigma - \ delta \ kappa - (\ rho + {\ bar {\ rho}}) \ sigma - (3 \ varepsilon - {\ bar {\ varepsilon}}) \ sigma + ( \ tau - {\ bar \ pi}} + {\ bar {\ alpha}} + 3 \ beta) \ kappa \ ،$

$\ Psi _ {1} = D \ beta - \ delta \ varepsilon - (\ alpha + \ pi) \ sigma - ({\ bar {\ rho}} - {\ bar {\ varepsilon}}) \ beta + (\ mu + \ gamma) \ kappa + ({\ bar {\ alpha}} - {\ bar {\ pi}}) \ varepsilon \ ،،$

$\ Psi _ {2} = {\ bar {\ delta}} \ tau - \ Delta \ rho - (\ rho {\ bar {\ mu}} + \ sigma \ lambda) + ({\ bar {\ beta} - \ alpha - {\ bar {\ tau}}) \ tau + (\ gamma + {\ bar {\ gamma}}) \ rho + \ nu \ kappa -2 \ Lambda \،$

$\ Psi _ {3} = {\ bar {\ delta}} \ gamma - \ Delta \ alpha + (\ rho + \ varepsilon) \ nu - (\ tau + \ beta) \ lambda + ({\ bar {\ gamma }} - {\ bar {\ mu}}) \ alpha + ({\ bar {\ beta}} - {\ bar {\ tau}}) \ gamma \ ،.$

$\ Psi _ {4} = \ delta \ nu - \ Delta \ lambda - (\ mu + {\ bar {\ mu}}) \ lambda - (3 \ gamma - {\ bar {\ gamma}}) \ lambda + (3 \ alpha + {\ bar {\ beta}} + \ pi - {\ bar {\ tau}}) \ nu \ ،.$

جایی که $\ لامبدا$ (استفاده برای $\ Psi _ {2$ ) به مقیاس انحنای NP اشاره دارد $\ لامبدا: = {\ frac {R} {24}$ که می تواند مستقیماً از متریک فضاسازی محاسبه شود $g_ {ab$ .

تفسیر بدنی [ ویرایش ]

سوکرز (1965) [8] تفسیری از اسکالرهای مختلف ویل در مسافت های بزرگ داد:

$\ Psi _ {2$ یک اصطلاح "Coulomb" است که نشان دهنده تک قطبی گرانشی منبع است.

$\ Psi _ {1$ و $\ Psi _ {3$ شرایط تابش "طولی" ورودی و خروجی هستند.

$\ Psi _ {0$ و $\ Psi_4$ شرایط تابش "عرضی" ورودی و خروجی هستند.

برای یک فضای عمومی بدون علامت مسطح حاوی اشعه ( پتروف نوع اول) ، $\ Psi _ {1$ و $\ Psi _ {3$ با انتخاب مناسب تتراد پوچ می توان به صفر تبدیل کرد. بنابراین این می تواند به عنوان مقادیر سنج مشاهده شود.

یک مورد به خصوص مهم مهم ترسناک ویل است $\ Psi_4$ . می توان نشان داد که تشعشع گرانشی خروجی (در یک فاصله زمانی بدون علامت مسطح) را توصیف می کند

$\ Psi _ {4} = {\ frac {1} {2}} \ left ({\ ddot {h}} _ {{{\ hat {\ theta}} {\ hat {\ theta}}}} - \ ddot {h} {_ {{{\ hat \ phi}} {\ hat \ phi}}} right \ Right) + i {\ ddot {h}} _ {{{\ hat {\tata} \ hat {\ phi}}}} = - - {\ ddot {h}} _ {+} + i {\ ddot {h}} _ {\ بار \.$

اینجا $h_ +$ و $ساعت_ بار$ قطبش های "به علاوه" و "متقاطع" از تشعشع گرانشی ، و نقاط دو نشان دهنده تمایز دو برابر است. [ نیاز به توضیح ]

با این حال ، نمونه های خاصی وجود دارد که تفسیر ذکر شده در بالا شکست می خورد. [9] اینها راه حلهای خلاء دقیقی از معادلات میدان انیشتین با تقارن استوانه ای هستند. به عنوان مثال ، یک استوانه ایستا (بی نهایت طولانی) می تواند یک میدان گرانشی تولید کند که نه تنها مؤلفه Wey مانند "Coulomb" مشابه انتظار داشته باشد. $\ Psi _ {2$ بلکه مؤلفه های "موج عرضی" ناپدید می شوند $\ Psi _ {0$ و $\ Psi_4$ . علاوه بر این ، امواج کاملاً خروجی انیشتین-روزن یک مؤلفه "موج عرضی ورودی" غیر صفر دارند $\ Psi _ {0$ .

منبع

https://en.wikipedia.org/wiki/Weyl_scalar

هرمان ویل

توسط علی رضا نقش نیلچی | یکشنبه بیست و نهم تیر ۱۳۹۹ | 23:50

هرمان ویل

بدنیا آمدن	هرمان کلاوس هوگو ویل 9 نوامبر 1885 المشورن ، امپراتوری آلمان
فوت کرد	8 دسامبر 1955 (70 سالگی) زوریخ ، سوئیس
ملیت	آلمانی
آلما ماده	دانشگاه گوتینگن
شناخته شده برای	لیست مباحث نامگذاری شده توسط هرمان ویل واقع بینانه ساختاری انتنتی [1] Wormhole
همسر (همسر)	فردریکه برته هلن جوزف (نام مستعار "هلا") (1893-1993) الن بور (نائل لوهشتاین) (1902-1988)
فرزندان	فریتز یواخیم ویل (1915-1915) مایکل ویل (1917–2011)
جوایز	عضو انجمن سلطنتی [2] جایزه لوباچفسکی (1927) سخنرانی گیبس (1948)
حرفه علمی
زمینه های	فیزیک ریاضی
موسسات	موسسه مطالعات پیشرفته دانشگاه گوتینگن ETH زوریخ
پایان نامه	Singuläre Integralgleichungen mit besonder Berücksichtigung des Fourierschen Integraltheorems (1908)
مشاور دکترا	دیوید هیلبرت [3]
دانشجویان دکترا	الكساندر وینشتین
سایر دانشجویان قابل توجه	Saunders Mac Lane
تأثیرات	امانوئل کانت [4] ادموند هوسرل [4] LEJ بروور [4]
امضا

هرمان کلاوس هوگو ویل ، ForMemRS [2] ( آلمانی: [vaɪl] ؛ 9 نوامبر 1885 - 8 دسامبر 1955) یک ریاضیدان آلمانی ، فیزیکدان نظری و فیلسوف بود . اگرچه بیشتر عمر کار خود را در زوریخ ، سوئیس و سپس پرینستون ، نیوجرسی گذراند ، اما او با سنت ریاضیات دانشگاه گوتینگن ، که توسط نمایندگان دیوید هیلبرت و هرمان مینکوفسکی نمایندگی شده است ، همراه است .

تحقیقات وی برای فیزیک نظری و همچنین رشته های صرفاً ریاضی از جمله نظریه اعداد از اهمیت عمده ای برخوردار بوده است . وی یکی از مؤثرترین ریاضیدانان قرن بیستم و عضو مهمی از انستیتوی مطالعات پیشرفته در سالهای اولیه بود. [5] [6] [7]

ویل کارهای فنی و برخی کلی را در مورد فضا ، زمان ، ماده ، فلسفه ، منطق ، تقارن و تاریخ ریاضیات منتشر کرد . او یکی از اولین کسانی بود که ارتباط نسبیت عام با قوانین الکترومغناطیس را تصور می کرد . در حالی که هیچ ریاضیدان نسل خود مایل به "جهان گرایی" هنری پوانکاره یا هیلبرت نبود ، ویل به اندازه هر کس نزدیک شد. [ بی طرفی است مورد مناقشه ] مایکل Atiyah، به ویژه ، اظهار داشته است که هر وقت او یک موضوع ریاضی را بررسی می کرد ، می فهمید که ویل بر او مقدم بوده است. [8]

فهرست

زندگینامه [ ویرایش ]

ویل در المشورن ، یک شهر کوچک در نزدیکی هامبورگ ، آلمان متولد شد و در Gymnasium Christianeum در Altona شرکت کرد . [9]

از سال 1904 تا 1908 در هر دو گوتینگن و مونیخ در رشته ریاضیات و فیزیک تحصیل کرد . دکترای وی در دانشگاه گوتینگن تحت نظارت دیوید هیلبرت که وی بسیار تحسین کرد ، اهدا شد .

در سپتامبر سال 1913 در گوتینگن ، ویل با فردریکه برته هلن جوزف ازدواج کرد (30 مارس 1893 [10] - 5 سپتامبر 1948 [11] ) که با نام هلن (نام مستعار "هلا") رفت. هلن دختر دکتر برونو ژوزف بود (سیزدهم دسامبر 1861 - 10 ژوئن 1934) ، پزشک معلمی که سمت Sanitätsrat را در ریبنیتز-دامگارتن آلمان نگه داشت. هلن یک فیلسوف بود (او شاگرد پدیدارشناس Edmund Husserl بود ) و مترجم ادبیات اسپانیایی به آلمانی و انگلیسی (به ویژه آثار فیلسوف اسپانیایی خوزه اورتگا و گاست ). [12] از طریق ارتباط نزدیک هلن با هوسرل بود که هرمان با تفکر هوسرل با (و بسیار تحت تأثیر آن) آشنا شد. هرمان و هلن دو پسر داشتند ،فریتز یواخیم ویل (19 فوریه 1915 - 20 ژوئیه 1977) و مایکل ویل (15 سپتامبر 1917 - 19 مارس 2011) ، [13] هر دو در زوریخ سوئیس متولد شدند. هلن در 5 سپتامبر 1948 در پرینستون ، نیوجرسی درگذشت. یک مراسم یادبود به افتخار او در 9 سپتامبر 1948 در پرینستون برگزار شد. سخنرانان در مراسم یادبود شامل پسرش فریتز یواخیم ویل و ریاضیدانان اسوالد وبلن و ریچارد کورانت بودند . [14] در سال 1950 هرمان با مجسمه ساز الن بور (نائل لوهشتاین) ازدواج کرد (17 آوریل 1902 - 14 ژوئیه 1988) ، [15] که بیوه استاد ریچارد جوزف بور (11 سپتامبر 1892 - 15 دسامبر 1940) بود [ 16] زوریخ.

پس از چند سال تدریس دروس تدریس ، ویل در سال 1913 گوتینگن را ترک کرد تا زوریخ صندلی ریاضیات را بگیرد [17] در ETH زوریخ ، جایی که او همکار آلبرت انیشتین بود ، که مشغول بررسی جزئیات نظریه نسبیت عام . انیشتین تأثیر ماندگاری در ویل داشت که مجذوب فیزیک ریاضی شد. در سال 1921 ویل با اروین شرودینگر ، فیزیکدان نظری که در آن زمان استاد دانشگاه زوریخ بود ملاقات کرد.. آنها به مرور زمان به دوستان نزدیک می شدند. ویل با همسر شرودینگر همسر آنماری (آنی) شرودینگر (née Bertel) رابطه جنسی عاشقانه ای داشت ، در همان زمان آنی در حال کمک به پرورش یک دختر نامشروع اروین به نام روت جورجی گری اریک مارس بود که در سال 1934 در آکسفورد انگلستان به دنیا آمد. . [18] [19]

ویل سخنگوی کامل کنگره بین المللی ریاضیدانان (ICM) در سال 1928 در بولونیا [20] و سخنگوی دعوت شده از ICM در سال 1936 در اسلو بود . وی در سال 1928 به عنوان یك عضو انجمن فیزیكی آمریكا انتخاب شد [21] و عضو آكادمی ملی علوم در سال 1940. [22] برای سال تحصیلی 1928-1929 وی استاد مهمان در دانشگاه پرینستون بود ، [23] كه در آنجا او مقاله ای با هوارد پی. رابرتسون نوشت . [24]

ویل در سال 1930 زوریخ را ترک کرد تا جانشین هیلبرت در گوتینگن شود و وقتی نازی ها در سال 1933 قدرت را به دست گرفتند ، به ویژه هنگامی که همسر وی یهودی بود ، رفت. به او در مؤسسه جدید مطالعات پیشرفته در پرینستون ، نیوجرسی ، یکی از اولین مقامهای اساتید ارائه شده بود ، اما به دلیل عدم تمایل به ترک میهن خود کاهش یافته بود. با اوج گرفتن اوضاع سیاسی در آلمان ، او نظر خود را تغییر داد و وقتی دوباره به مقام پیشنهاد شد ، پذیرفت. وی تا زمان بازنشستگی در سال 1951 در آنجا ماند. همراه او با همسر دوم الن ، وقت خود را در پرینستون و زوریخ گذراند و در 8 دسامبر سال 1955 در حالی که در زوریخ زندگی می کرد در اثر حمله قلبی درگذشت.

ویل در 12 دسامبر سال 1955 در زوریخ Created شد . [25] خدمه وی در دستان خصوصی ماندند [ منبع غیرقابل اعتماد؟ ] تا سال 1999، در آن زمان آنها در طاق دخمه مردگان در فضای باز در دفن شدهاند گورستان پرینستون . [26] بقایای فرزند هرمان مایکل ویل (2011-1991) درست در کنار خاکستر هرمان در همان طاق کلمبیایی منتقل می شود.

ویل یک پناهیست بود . [27]

مشارکت ها [ ویرایش ]

این بخش برای تأیید نیاز به استناد اضافی دارد . لطفاً با افزودن استناد به منابع معتبر ، این مقاله را بهبود بخشید . اطلاعات بدون مرجع ممکن است مشکل ایجاد کرده و پاک شوند. یافتن منابع: "هرمان ویل" - اخبار · روزنامه ها · کتاب ها · محقق · JSTOR
( فوریه 2017 ) ( یاد بگیرید چگونه و چه زمانی این پیام الگوی را حذف کنید )

هرمان ویل (چپ) و ارنست پشل (راست).

توزیع مقادیر ویژه [ ویرایش ]

اطلاعات بیشتر: قانون Weyl و قانون Weyl j حدس Weyl

در سال 1911 ویل انتشار Über die asymptotische Verteilung der Eigenwerte ( در مورد توزیع بدون علامت ویژه مقادیر ویژه ) را نشان داد که در آن ثابت کرد که مقادیر ویژه لاپلاسیان در دامنه جمع و جور مطابق قانون به اصطلاح Weyl توزیع می شوند . وی در سال 1912 براساس اصول گوناگونی اثبات جدیدی ارائه داد. ویل چندین بار به این موضوع بازگشت ، سیستم الاستیسیته را در نظر گرفت و حدس ویل را تدوین کرد . این آثار توزیع بی اهمیت دامنه از مقادیر ویژه از تجزیه و تحلیل مدرن را آغاز کردند.

مبانی هندسی مانیفولدز و فیزیک [ ویرایش ]

اطلاعات بیشتر: تبدیل Weyl و Tensor Weyl

در سال 1913 ، ویل Die Idee der Riemannschen Fläche ( مفهوم یک سطح ریمان ) را منتشر کرد ، که به درمان یکپارچه ای از سطوح ریمان پرداخت . در آن ویل از توپولوژی مجموعه ای برای تعیین دقیق تر نظریه سطح ریمان استفاده کرد ، مدلی که در ادامه کار روی مانیفولد ها دنبال می شود . او به همین منظور کارهای اولیه LEJ Brouwer در توپولوژی را جذب کرد .

ویل به عنوان یکی از چهره های اصلی مکتب گوتینگن ، از ابتدای فعالیت خود کاملاً مورد تأیید کار اینشتین بود. او پیشرفت فیزیک نسبیت را در سال 1918 در Raum، Zeit، Materie ( فضا ، زمان ، ماده ) خود دنبال کرد و در سال 1922 به چاپ چهارم رسید. در سال 1918 ، او مفهوم سنج را معرفی کرد و اولین نمونه از آنچه اکنون است معروف به یک نظریه سنج است . نظریه سنج ویلی تلاشی ناموفق برای مدل سازی میدان الکترومغناطیسی و میدان گرانشی به عنوان خصوصیات هندسی فضا بود . تانسور Weyl در هندسه ریمانیاز اهمیت عمده ای در درک ماهیت هندسه کنفورماسی برخوردار است. در سال 1929 ، ویل مفهوم vierbein را به نسبیت عام معرفی کرد. [28]

رویکرد کلی خود را در فیزیک بر پایهی پدیدارشناسی فلسفه ادموند هوسرل ، به طور خاص هوسرل 1913 ی ideen زو einer reinen Phänomenologie UND phänomenologischen فلسفه. Erstes Buch: Allgemeine Einführung in die reine Phänomenologie (ایده های یک پدیدارشناسی ناب و فلسفه پدیدارشناسی. کتاب اول: مقدمه عمومی). هوسرل به انتقاد گوتلوب فرگه به شدت در مورد نخستین اثر خود در مورد فلسفه حسابی واکنش جدی نشان داده بود و در حال بررسی حس ریاضی و ساختارهای دیگر بود ، که فرگه از مرجع تجربی متمایز کرده بود. [ نیاز به استناد ]

گروه های توپولوژیک ، گروه های دروغ و تئوری نمایندگی [ ویرایش ]

مقاله اصلی: پیتر ویل قضیه ، گروه ویل ، spinor ویل ، و جبر ویل

از سال 1923 تا 1938 ، ویل تئوری گروه های جمع و جور ، از نظر بازنمایی ماتریس را توسعه داد . در مورد گروه جمع و جور دروغ ، او فرمول شخصیت اساسی را ثابت کرد .

این نتایج در درک ساختار تقارن مکانیک کوانتومی اساسی است که وی بر اساس تئوری گروهی قرار داده است. این شامل اسپینورها بود . همراه با فرمول ریاضی مکانیک کوانتومی در مقیاسی بزرگ به دلیل جان فون نویمان ، این درمان آشنا داد از حدود سال 1930. گروه های غیر جمع و جور و نمایندگی خود را، به ویژه گروه هایزنبرگ ، همچنین در این زمینه خاص شده بودند، در خود 1927 کمیت ویل ، بهترین پل بین فیزیک کلاسیک و کوانتومی تا به امروز. از این زمان ، و مطمئناً به کمک نمایشگاههای ویل ، گروه های دروغ و جبرهای دروغ بسیار کمک شده استهر دو ریاضیات محض و فیزیک نظری به یک بخش اصلی تبدیل شدند .

کتاب او گروه های کلاسیک نظریه ثابت را مجددا مورد بررسی قرار داده است . آن را پوشش داده گروه متقارن ، گروه کلی خطی ، گروه های متعامد و گروه ها symplectic و نتایج را بر روی خود ویژگیهای و تضمینی .

تحلیل هارمونیک و نظریه شماره تحلیلی [ ویرایش ]

اطلاعات بیشتر: ملاک ویل

ویلی همچنین با استفاده از معیار خود برای توزیع یکنواخت mod 1 ، که یک گام اساسی در تئوری اعداد تحلیلی بود ، نحوه استفاده از مبالغ نمایی در تقریب دیوفانتین را نشان داد . این کار به عملکرد zema ریمان و همچنین نظریه شماره افزودنی اعمال شده است . توسط بسیاری دیگر ساخته شده است.

مبانی ریاضیات [ ویرایش ]

در زنجیره ویل منطق توسعه تجزیه و تحلیل اخباری با استفاده از سطوح پایین تر از برتراند راسل را نظریه منشعب از انواع . او قادر به توسعه بسیاری از حساب دیفرانسیل و انتگرال کلاسیک بود، در حالی که با استفاده از نه اصل موضوع انتخاب و نه اثبات با تناقض ، و اجتناب از گئورگ کانتور را مجموعه های نامحدود . ویل در این دوره از ساختارگرایی رادیکال ایده آل گرایانه عاشقانه ، فیچت آلمانی ، فیچت خواست .

اندکی پس از انتشار «Continuum Weyl» به طور خلاصه موقعیت خود را کاملاً به شهودگرایی بروو تغییر داد. در زنجیره ، امتیاز constructible به عنوان نهادهای گسسته وجود داشته باشد. ویل یک پیوستار را می خواست که مجموع امتیازات نیست. او مقاله جنجالی نوشت و اعلام كرد كه ، برای خودش و لژ بروو ، "ما انقلاب هستیم". [ نیاز به استناد ] این مقاله در تبلیغ دیدگاه های شهودی نسبت به آثار اصلی خود بروور بسیار مؤثر است.

جورج پولیا و ویل ، در طی یک گردهمایی ریاضیدانان در زوریخ (9 فوریه 1918) ، در مورد جهت آینده ریاضیات شرط بندی کردند. ویل پیش بینی کرد که در 20 سال بعد ، ریاضیدانان متوجه می شوند که کل مبهم بودن مفاهیمی مانند اعداد واقعی ، مجموعه ها و شمارش معقولات چیست و علاوه بر این ، سؤال در مورد حقیقت یا غلط بودن حداقل خاصیت فوقانیاعداد واقعی است. به همان اندازه که پرسیدن درباره حقیقت ادعاهای اساسی هگل در فلسفه طبیعت معنی دار است. [29] هر پاسخی برای چنین سؤالی غیرقابل توصیف ، بی ربط با تجربه و در نتیجه بی معنا خواهد بود.

با این حال ، طی چند سال ویل تصمیم گرفت که شهودگرایی Brouwer محدودیت های زیادی را در ریاضیات ایجاد کند ، همانطور که همیشه منتقدین گفته اند. مقاله "بحران" معلم فرمالیست ویل را هیلبرت ناراحت کرده بود ، اما بعدها در دهه 1920 ویل بخشی از موقعیت خود را با وضعیت هیلبرت آشتی داد.

بعد از حدود 1928 ویل ظاهرا تصمیم گرفته بود که شهود گرایی ریاضی بود سازگار با شور و شوق خود را برای نمی پدیدارشناسی فلسفه هوسرل ، به عنوان او فکر ظاهرا زودتر بود. ویل در دهه های آخر عمر خود بر ریاضیات به عنوان "ساخت نمادین" تأکید کرد و نه تنها به هیلبرت بلکه به ارنست کاسیرر نزدیک تر شد . اما ویل به ندرت به کاسیر اشاره می کند ، و فقط مقالات و بندهایی مختصر برای بیان این موضع نوشت.

تا سال 1949 ، ویل کاملاً از ارزش نهایی شهود گری سرخورده شد و نوشت: "ریاضیات با بروو بالاترین وضوح شهودی خود را به دست می آورد. او موفق می شود تا آغاز تجزیه و تحلیل را به روشی طبیعی توسعه دهد ، همه وقت ارتباط را با شهود بسیار بیشتر حفظ می کند. با این وجود نمی توان انکار کرد که در پیشبرد تئوری های بالاتر و عمومی تر ، عدم استفاده از قوانین ساده منطق کلاسیک سرانجام منجر به تقریباً غیرقابل تحمل می شود. بنای برج او که اعتقاد بر این است که از بلوک های بتونی ساخته شده است ، قبل از چشمانش در غبار حل می شود. "

فرمین های ویل [ ویرایش ]

مقاله اصلی: ویل فرمیون

در سال 1929 ، ویل فرمیون را برای استفاده در یک نظریه جایگزینی برای نسبیت پیشنهاد داد. این فرمیون یک قطعه ذرات بدون جرم و بار الکتریکی است. یک الکترون می تواند به دو فرمون Weyl تقسیم شود یا از دو فرمون Weyl تشکیل شود. نوترینوها یک بار تصور می شد که فرمیونها ویل، اما آنها در حال حاضر شناخته شده اند که جرم است. فرمینون های ویل برای برنامه های الکترونیکی به دنبال حل مشکلات موجود در الکترون هستند. چنین قطعات جزئی در سال 2015 کشف شد ، به شکلی از کریستال های معروف به نیمه های ویلی ، نوعی ماده توپولوژیکی. [30] [31] [32]

نقل قول ها [ ویرایش ]

سوال مبانی نهایی و معنای نهایی ریاضیات باز است. ما نمی دانیم که در چه جهاتی راه حل نهایی خود را پیدا خواهد کرد و حتی اصلاً نمی توان از یک هدف نهایی نهایی انتظار داشت. "ریاضیات" ممکن است یک فعالیت خلاق انسان ، مانند زبان یا موسیقی ، از اصالت اولیه باشد ، که تصمیمات تاریخی آن مخالف عقلانیت عینی کامل است.

- Gesammelte Abhandlungen —as به نقل از کتاب سال - انجمن فلسفی آمریکا ، 1943 ، ص. 392

در این روزها فرشته توپولوژی و شیطان جبر انتزاعی برای روح هر حوزه ریاضی فردی می جنگند. ویل (1939b ، ص 500)

کتابشناسی [ ویرایش ]

1911. dieber die asymptotische Verteilung der Eigenwerte ، Nachrichten der Königlichen Gesellschaft der Wissenschaften zu Göttingen، 110-117 (1911).
1913. Die Idee der Riemannschen Flāche ، [33] 2d 1955. Concept of a Riemann Surface . آدیسون وسلی.
1918. Das Kontinuum ، trans. 1987 The Continuum: یک بررسی مهم از بنیاد تحلیل . شابک 0-486-67982-9
1918. راوم ، زیت ، مادری . 5 عدد به سال 1922 ویرایش. با یادداشت های یورگن ایلرز ، 1980. trans. 4 edn. هنری بروس ، ماده زمان فضایی در سال 1922 ، Methuen ، rept. 1952 داور. شابک 0-486-60267-2 .
1923. Mathematische Analyze des Raumproblems .
1924. آیا ist Materie بود؟
1925. (انتشار: 1988 ویرایش K. Chandrasekharan) Geometrische Idee از ریمان .
1927. Philosophie der Mathematik und Naturwissenschaft ، edd 2d. 1949. فلسفه ریاضیات و علوم طبیعی ، پرینستون 0689702078. با مقدمه جدیدی از فرانك ویلكسك ، انتشارات دانشگاه پرینستون ، 2009 ، ISBN 978-0-691-14120-6 .
1928. Gruppentheorie und Quantenmechanik . ترجمه توسط HP Robertson، Theory of Groups and Quantum Mechanics ، 1931، rept. 1950 داور. شابک 0-486-60269-9
1929. "Elektron und Gravitation I" ، Zeitschrift Physik ، 56 ، صص 330-352. - معرفی vierbein به GR
1933. یل جهان باز ، خزندگان. 1989 Oxbow Press ISBN 0-918024-70-6
1934. ذهن و طبیعت ایالات متحده از پنسیلوانیا پرس.
1934. "در ماتریس های عمومی ریمان ،" آن. ریاضی. 35 : 400-415.
1935. تئوری ابتدایی invariants .
1935. ساختار و نمایندگی گروه های مداوم: سخنرانی در دانشگاه پرینستون طی سالهای 1933-343 .
ویل ، هرمان (1939) ، گروه های کلاسیک. ISarian و انتشارات آنها ، انتشارات دانشگاه پرینستون ، ISBN 978-0-691-05756-9، MR 0000255 [34]
ویل ، هرمان (1939b) ، "ثابت" ، مجله ریاضیات دوک ، 5 (3): 489-502 ، doi : 10.1215 / S0012-7094-39-00540-5 ، ISSN 0012-7094 ، MR 0000030
1940. تئوری جبری اعداد ، خزندگان. 1998 پرینستون یو. پرس. شابک 0-691-05917-9
ویل ، هرمان (1950) ، "تأخیر ، پیر و جدید ، از مسئله مقادیر ویژه" ، گاو نر. عامر ریاضی. انجمن ، 56 (2): 115–139 ، doi : 10.1090 / S0002-9904-1950-09369-0(متن سخنرانی جوزیا ویلارد گیبس در سال 1948 )
1952. تقارن . انتشارات دانشگاه پرینستون. شابک 0-691-02374-3
1968. در K. Chandrasekharan ed ، Gesammelte Abhandlungen . جلد چهارم آبپاش

همچنین مشاهده کنید [ ویرایش ]

مباحث به نام هرمان ویل [ ویرایش ]

مقاله اصلی: لیست مواردی که به نام هرمان ویل نامگذاری شده است

ماژورنا- ویل اسپینور
قضیه پیتر – ویل
دوگانگی Schur-Weyl
جبر ویل
پایه ویل از ماتریس گاما
اتاق ویل
فرمول شخصیت ویلی
معادله ویل ، یک معادله موج نسبی
ویل فرمیون
سنج ویل
گرانش ویل
نماد ویل
کمیت ویل
ویل اسپینور
ویل جمع ، نوعی از مبلغ نمایی
تقارن ویل : به تحول ویل نگاه کنید
تایلر ویل
تبدیل ویل
تحول ویل
قضیه ویل - شوتن
ملاک ویل
لیم ویل در مورد کمبود خون
لیم ویلی در مورد "بسیار ضعیف" معادله لاپلاس

منابع

https://en.wikipedia.org/wiki/Hermann_Weyl

اصل کاوالیری

توسط علی رضا نقش نیلچی | جمعه بیست و هفتم تیر ۱۳۹۹ | 20:28

دو پشته سکه های انگلیس با همان حجم ، که اصل کاوالیری را در سه بعد نشان می دهد

در هندسه ، اصل کاوالیری ، اجرای مدرن از روش indivisibles ، به نام Bonaventura Cavalieri ، به شرح زیر است: [1]

مورد 2 بعدی : فرض کنید دو منطقه در یک هواپیما بین دو خط موازی در آن هواپیما قرار دارد. اگر هر خط به موازات این دو خط ، هر دو منطقه را در بخش های با طول مساوی تقاطع کند ، دو منطقه دارای مساوی هستند.
مورد 3 بعدی : فرض کنید دو منطقه در سه فضا (جامدات) بین دو هواپیمای موازی قرار دارند. اگر هر هواپیما به موازات این دو هواپیما ، هر دو منطقه را در مقطع مساحت مساوی تقاطع کند ، دو منطقه دارای حجم برابر هستند.

امروزه اصل کاوالیری به عنوان گامی اولیه در جهت حسابگر انتگرال تلقی می شود ، و در حالی که از بعضی اشکال مانند تعمیم آن در قضیه فوبینی استفاده می شود ، نتایج با استفاده از اصل کاوالیری اغلب می تواند مستقیماً از طریق ادغام نشان داده شود. در جهت دیگر ، اصل کاوالیری از روش یونانی باستان فرسودگی خارج شد ، که از محدودیتهایی استفاده می کرد اما از infinitesimals استفاده نمی کرد .

فهرست

تاریخچه [ ویرایش ]

Bonaventura Cavalieri ، ریاضیدان این اصل نام دارد.

اصل کاوالیری در ابتدا به روش غیرقابل تقسیم نامگذاری می شد ، نامی که در اروپای رنسانس شناخته می شد . کاوالیری تئوری کاملی از غیرقابل توصیف را توسعه داد ، که در Geometria indivisibilibus continorum nova quadam ratione promota ( Geometry ، به روش جدیدی توسط indivisibles of the Continua ، 1635) و Exercitationes Geometae جنس خود توضیح داد ( شش تمرین هندسی ، 1647). [2] در حالی که کار کاوالیری این اصل را بنا نهاده بود ، در انتشارات خود او را تکذیب کرد که زنجیره ای از جزء به منظور اجتناب از پارادوکس های مرتبط و مشاجرات مذهبی ساخته شده است و او از آن برای یافتن نتایج قبلاً ناشناخته استفاده نمی کند. [3]

در قرن 3 قبل از میلاد ، ارشمیدس با استفاده از روشی که شبیه به اصل کاوالیری است ، [4] با توجه به حجم یک مخروط و استوانه در کار خود با عنوان روش مضامین مکانیکی ، توانست حجم یک کره را پیدا کند . در قرن 5 میلادی ، زو چونگزی و پسرش زو چنگشی روش مشابهی برای یافتن جلوی کره ایجاد کردند. [5] انتقال از قرار indivisibles کاوالیری به اوانجلیستا توریچلی را و جان والیس را بینهایت یک پیشرفت عمده در تاریخ بود حساب دیفرانسیل و انتگرال . افراد غیرقابل مشاهده اشخاص تجسمی بودند1 ، به طوری که تصور می شد شکل هواپیما از بینهایت خطوط 1 بعدی ساخته شده است. در همین حال ، infinitesimals موجوداتی با همان ابعادی بودند که شکل می دهند. بنابراین ، یک شکل هواپیما می تواند از "موازی" از عرض نامتناهی ساخته شود. با استفاده از فرمول جمع حاصل از پیشرفت حسابی ، والیس مساحت یک مثلث را با تقسیم آن در موازی های نامتناهی از عرض 1 / uted محاسبه کرد.

مثالها [ ویرایش ]

کره [ ویرایش ]

سطح مقطع دیسک شکل کره همان ناحیه با سطح مقطع حلقه شکل آن قسمت از استوانه را دارد که در خارج از مخروط قرار دارد.

اگر کسی بداند که حجم مخروط است ${\ frac {1} {3}} \ سمت چپ ({\ متن {پایه}} \ بار {\ متن {ارتفاع}} \ سمت راست)$ سپس می توان از اصل کاوالیری استفاده کرد تا این واقعیت را داشته باشد که حجم یک کره است ${\ frac {4} {3}} \ pi r ^ {3}$ ، جایی که $r$ شعاع است

که به شرح زیر انجام می شود: حوزه ای از شعاع را در نظر بگیرید $r$ و یک سیلندر شعاع $r$ و قد $r$ . درون سیلندر مخروطی است که جلوی آن در مرکز یک پایه استوانه است و پایه آن پایه دیگر استوانه است. توسط قضیه فیثاغورسی ، این هواپیما واقع شده است $ی$ واحدهای بالاتر از "استوا" در یک کره از حلقه در منطقه قرار دارند $\ pi \ سمت چپ (r ^ {2} -y ^ {2} \ سمت راست)$ . مساحت تقاطع هواپیما با بخشی از استوانه که خارج از مخروط است نیز قرار دارد $\ pi \ سمت چپ (r ^ {2} -y ^ {2} \ سمت راست)$ . همانطور که می بینیم مساحت هر تقاطع دایره با صفحه افقی که در هر بلندی واقع شده است $ی$ مساحت تقاطع هواپیما با بخشی از استوانه که خارج از مخروط است برابر است. بنابراین ، با استفاده از اصل کاوالیری ، می توان گفت که حجم کره نیم برابر است با حجم بخشی از استوانه که "خارج" مخروط است. حجم فوق مخروط فوق است $\ frac {1} 3}}$ از حجم استوانه ، بنابراین حجم خارج از مخروط است

$\ frac {2} 3}}$ حجم سیلندر بنابراین حجم نیمه بالایی کره است $\ frac {2} 3}}$ حجم سیلندر حجم سیلندر است

$\ متن {پایه}} \ بار {\ متن {ارتفاع}} = \ pi r ^ {2} \ cdot r = \ pi r ^ {3$

("پایگاه" در واحد مساحت است ؛ "ارتفاع" در واحدهای مسافت است . مساحت × فاصله = حجم.)

بنابراین حجم نیمه فوقانی است $\ displaystyle {\ frac {2} {3}} \ pi r ^ {3}$ و کل کره است ${\ frac {4} {3}} \ pi r ^ {3}$ .

مخروط و هرم [ ویرایش ]

این واقعیت که حجم هر هرم ، صرف نظر از شکل پایه ، چه دایره ای شکل در مورد مخروط ، یا مربع مانند در مورد اهرام مصر ، یا هر شکل دیگر ، (1/3) پایه × ارتفاع ، می تواند با اصل کاوالیری برقرار شود ، اگر کسی فقط می داند که در یک مورد صادق است. ممکن است ابتدا با تقسیم فضای داخلی یک منشور مثلثی به سه مؤلفه هرمی با حجم مساوی ، آن را در یک مورد واحد ایجاد کند. ممکن است با استفاده از اصل کاوالیری برابری آن سه جلد را نشان دهد.

در واقع، استدلال بینهایت اصل یا مشابه کاوالیری است لازم برای محاسبه حجم مخروط و حتی اهرام است که اساسا محتوای، مشکل سوم هیلبرت - اهرام چند وجهی و مخروط نمی تواند قطع و دوباره مرتب به شکل استاندارد، و به جای آن باید مقایسه شود به معنی بی نهایت (بی نهایت) یونانیان باستان از روشهای مختلف پیش ساز مانند استدلالهای مکانیکی Archimedes یا روش فرسودگی برای محاسبه این حجمها استفاده می کردند.

مشکل حلقه دستمال [ ویرایش ]

مقاله اصلی: مشکل حلقه دستمال

اگر یک سوراخ از ارتفاع h مستقیماً از طریق مرکز یک کره حفر شود ، حجم باند باقی مانده به اندازه کره بستگی ندارد. برای یک حوزه بزرگتر ، باند نازک تر اما طولانی تر خواهد بود.

در آنچه که حلقه حلقه دستمال نامیده می شود ، با اصل کاوالیری نشان داده می شود که وقتی یک سوراخ مستقیم از مرکز یک کره حفر شود که باند باقی مانده دارای ارتفاع h باشد ، حجم مواد باقیمانده به طور شگفت آور بستگی به اندازه آن ندارد. کره. سطح مقطع حلقه باقیمانده یک حلقه هواپیما است که مساحت آن تفاوت بین نواحی دو دایره است. با قضیه فیثاغورس ، مساحت یکی از دو دایره π برابر r 2 - y 2 است ، در جایی که r شعاع کره و y فاصله آن از صفحه استوا تا هواپیما برش است و از طرف دیگر است. πبار r 2 - ( h / 2) 2 . هنگامی که این موارد از بین برود ، r 2 لغو می شود. از این رو عدم وابستگی به پاسخ خط پایین به r .

سیکلوئیدها [ ویرایش ]

سطح مقطع افقی منطقه محدود شده توسط دو قوس حلقوی ردیابی شده توسط یک نقطه در همان دایره که در یک مورد در جهت عقربه های ساعت در خط زیر آن می چرخد ، و در دیگری در جهت عقربه های ساعت در خط بالای آن ، طول آن با طول مشابه است. سطح مقطع افقی دایره.

N. رید نشان داده است [6] چگونه برای پیدا کردن مساحت محدود شده توسط سیکلوئید با استفاده از اصل کاوالیری. دایره شعاع rمی تواند در جهت عقربه های ساعت بر روی خط زیر آن یا در جهت خلاف جهت عقربه های ساعت بر روی یک خط بالاتر از آن بچرخد. نقطه ای از دایره به این ترتیب دو سیکلوئید را مشخص می کند. هنگامی که دایره مسافت خاصی را چرخانده است ، زاویه ای که از طریق آن می توانست به جهت عقربه های ساعت چرخانده شود و آن که از طریق آن می توانست خلاف جهت عقربه های ساعت باشد همان است. بنابراین دو نقطه ردیابی سیکلوئیدها در ارتفاعات مساوی هستند. بنابراین خط از طریق آنها افقی است (یعنی به موازات دو خط که دایره روی آن می چرخد). در نتیجه ، هر مقطع افقی دایره دارای طول یکسان با سطح مقطع افقی مربوطه از منطقه است که توسط دو قوس سیویید محدود شده است. براساس اصل کاوالیری ، این دایره مساحتی برابر با آن منطقه دارد.

مستطیل را در نظر بگیرید که یک قوس تک حلقوی محدود دارد. از تعریف یک سیکلوئید ، عرض 2π r و ارتفاع 2 r داردبنابراین مساحت آن چهار برابر مساحت دایره است. مساحت این مستطیل را که در بالای قوس سیکلوئید قرار دارد محاسبه کنید با مستحکم کردن مستطیل در نقطه میانی که قوس با مستطیل در آن قرار دارد ، یک قطعه را با 180 درجه بچرخانید و نیمه دیگر مستطیل را با آن بپیچانید. مستطیل جدید ، به مساحت دو برابر دایره ، از منطقه "عدسی" بین دو سیکلوئید تشکیل شده است که مساحت آن در بالا محاسبه شده است که همان دایره است و دو منطقه ای که منطقه را بالای قوس سیکلوئید تشکیل داده اند. در مستطیل اصلی. بنابراین ، ناحیه محدود شده توسط یک مستطیل در بالای یک قوس کامل از سیکلوئید دارای مساحتی برابر با منطقه دایره است و بنابراین ، منطقه محدود به طاق سه برابر مساحت دایره است.

منبع

https://en.wikipedia.org/wiki/Cavalieri%27s_principle

دنباله استورم

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 23:0

در ریاضیات ، دنباله استورم از یک چند جمله ای p یک متغیره ، دنباله ای از چندجمله ای مرتبط با p و مشتق آن با یک نوع از الگوریتم اقلیدس برای چندجمله ای است . قضیه استورم بیان تعداد متمایز واقعی ریشه ازp واقع در یک فاصله زمانی از نظر تعدادی از تغییرات نشانه هایی از ارزش های دنباله استورم در مرزهای فاصله. با استفاده از فاصله همه اعداد واقعی ، تعداد کل ریشه های واقعی p را نشان می دهد . [1]

در حالی که قضیه اساسی جبر به راحتی تعداد کلی ریشه های پیچیده را که با کثرت شمارش می شود ، به دست می آورد ، روشی برای محاسبه آنها ارائه نمی دهد. قضیه استورم تعداد ریشه های واقعی متمایز را شمرده و آنها را در فواصل زمانی قرار می دهد. با تقسیم فواصل حاوی برخی از ریشه ها ، می توان ریشه ها را در فواصل کوچک دلخواه جدا کرد که هر یک دقیقاً یک ریشه دارد. این بازده قدیمی ترین الگوریتم جداسازی ریشه واقعی و الگوریتم دقیق یافتن ریشه برای چندجمله ای یک متغیره است.

برای محاسبه طول اعداد حقیقی ، قضیه استورم کارآمد کمتر از روش های دیگر بر اساس است حکومت دکارت از نشانه . با این حال ، آن را در هر زمینه بسته واقعی کار می کند ، و بنابراین ، برای مطالعه نظری پیچیدگی محاسباتی از تجزیه پذیری و حذف کمی در تئوری مرتبه اول اعداد واقعی اساسی است.

توالی استورم و قضیه استورم به نام ژاک چارلز فرانسوا استورم نامگذاری شده است که در سال 1829 قضیه را کشف کرد. [2]

فهرست

قضیه [ ویرایش ]

زنجیره استورم و یا توالی استورم یک چند جمله ای های تک متغیری (P ( X با ضرایب حقیقی دنباله ای از چند جمله ای است ${\ displaystyle P_ {0} ، P_ {1} ، \ ldots ،$ به طوری که

$\ displaystyle {\ شروع {تراز شده} P_ {0} & = P ، \\ P_ {1} & = P '، \\ P_ {i + 1} & = - \ operatorname {rem} (P_ {i-1 } ، P_ {i}) ، \ end {تراز شده}}}$

برای من ≥ 1 ، که در آن P ' است مشتق از P ، و ${\ displaystyle \ operatorname {rem} (P_ {i-1} ، P_ {i})}$ باقی مانده از است تقسیم اقلیدسی از $P _ {{i-1}$ توسط ${\ displaystyle P_ {i}.}$ طول دنباله Sturm حداکثر درجه P است .

تعداد تغییرات علامت در ξ دنباله Sturm از P تعداد تغییرات علامت-نادیده گرفتن صفرها در دنباله اعداد واقعی است

${\ displaystyle P_ {0} (\ xi) ، P_ {1} (\ xi) ، P_ {2} (\ xi) ، \ ldots.$

این تعداد از علائم در اینجا( V ( ξ مشخص شده است .

کشورهای قضیه استورم که اگر P است چند جمله ای رایگان مربع ، تعداد ریشه حقیقی متمایز از P در فاصله نیمه باز ( ، ب ] است [1]

قضیه با تعیین علامت در + ∞ چند جمله ای به عنوان علامت ضریب پیشرو آن (به عنوان مثال ضریب اصطلاح بالاترین درجه) به فواصل نامحدود گسترش می یابد . در -∞ نشانه ای از یک چند جمله ای به نشانه ضریب پیشرو آن برای یک چند جمله ای حتی درجه، و علامت مخالف برای یک چندجملهای از درجه فرد است.

در مورد یک چند جمله ای غیر آزاد مربع، اگر نه و نه ب ریشه های متعدد از است p ، پس از آن V ( ) - V ( ب ) تعداد است متمایز ریشه های حقیقی P .

اثبات قضیه به شرح زیر است: وقتی مقدار x از a به b افزایش یابد ، ممکن است از صفر برخی عبور کند $P_ {من$ ( i > 0 )؛ وقتی این اتفاق می افتد ، تعداد تغییرات علامت از $display \ displaystyle (P_ {i-1 ، P_ {i} ، P_ {i + 1})}$ تغییر نمی کند. وقتی x از یک ریشه عبور می کند ${\ نمایشگر P_ {0} = P ،$ تعداد تغییرات علائم $display \ displaystyle (P_ {0} ، P_ {1})}$ از 1 به 0 کاهش می یابد. این تنها مقادیر x است که ممکن است برخی از علائم تغییر کند.

مثال [ ویرایش ]

فرض کنید ما می خواهیم تعداد ریشه ها را در چند دامنه برای چند جمله ای پیدا کنیم $p (x) = x ^ {4} + x ^ {3} -x-1$ . بنابراین

${\ شروع {تراز شده} p_ {0} (x) & = p (x) = x ^ {4} + x ^ {3} -x-1 \\ p_ {1} (x) & = p '(x ) = 4x ^ {3} + 3x ^ {2} -1 \ end {تراز شده}}$

باقی مانده از تقسیم اقلیدسی از p 0 توسط p 1 است $\ displaystyle - {\ tfrac {3} {16}} x ^ {2} - {\ tfrac {3} {4}} x - {\ tfrac {15} 16}}}؛}$ ضرب آن را با 1 پوند بدست می آوریم

$p_ {2} (x) = {\ tfrac {3} 16}} x ^ {2} + {\ tfrac {3} {4}} x + {\ tfrac {15} 16}}$ .

تقسیم بعدی p 1 بر p 2 و ضرب باقیمانده توسط − 1 ، به دست می آوریم

$p_ {3} (x) = - 32x-64$ .

اکنون p 2 را بر p 3 تقسیم می کنیم و باقیمانده را با − 1 ضرب می کنیم ، به دست می آوریم

$p_ {4} (x) = - {\ tfrac {3} 16}$ .

از آنجا که این یک ثابت است ، این محاسبه محاسبات دنباله استورم را تمام می کند.

برای پیدا کردن تعداد ریشه های واقعی $p_ {0$ یکی به ارزیابی توالی از نشانه های این چند جمله ای در -∞ و ∞ ، که به ترتیب (+، -، +، +، -) و (+، +، +، -، -) . بدین ترتیب

$\ displaystyle V (- \ infty) -V (+ \ infty) = 3-1 = 2 ،$

که نشان می دهد p دارای دو ریشه واقعی است.

این امر را می توان با ذکر این نکته تأیید کرد که p ( x ) را می توان به عنوان ( x 2 - 1) ( x 2 + x + 1) تعیین کرد ، جایی که عامل اول دارای ریشه −1 و 1 است و فاکتور دوم ریشه واقعی ندارد. این آخرین ادعا از فرمول درجه دوم و همچنین از قضیه اشتورم حاصل می شود که توالی های علامت (+ ، - ، -) را در −∞ و (+ ، + ، -) در + gives به دست می دهد .

تعمیم [ ویرایش ]

توالی Sturm از دو جهت تعمیم یافته است. برای تعریف هر چند جمله ای در دنباله ، Sturm از منفی باقی مانده تقسیم اقلیدسی دو مورد قبلی استفاده کرد. این قضیه صادق است اگر کسی منفی باقیمانده را توسط محصول یا مقدار آن با یک ثابت مثبت یا مربع چند جمله ای جایگزین کند. همچنین در نظر گرفتن سکانس هایی که چند جمله ای دوم مشتق اول نیست ، مفید است (در زیر مراجعه کنید).

توالی استورم تعمیم یک دنباله متناهی از چند جمله ای با ضرایب حقیقی است

${\ displaystyle P_ {0} ، P_ {1} ، \ نقطه ، P_ {m}$

به طوری که

درجه بعد از درجه اول کاهش می یابد: $\ displaystyle \ deg P_ {i} <\ deg P_ {i-1}}$ برای i = 2 ، ... ، m ؛
$P_m$ هیچ ریشه واقعی ندارد و یا نشانه ای را در نزدیکی ریشه واقعی خود تغییر نمی دهد.
اگر P i ( ξ ) = 0 برای 0 < i < m و ξ یک عدد واقعی باشد ، P P - 1 ( ξ ) P i + 1 ( ξ ) <0 .

شرط آخر دلالت بر این دارد که دو چند جمله ای متوالی هیچ ریشه واقعی مشترکی ندارند. به طور خاص ، توالی اصلی استورم یک توالی استورم تعمیم یافته است ، اگر (و تنها در صورت این کار) چند جمله ای دارای ریشه واقعی چندگانه نیست (در غیر این صورت ، دو چند جمله ای اول دنباله استورم دارای یک ریشه مشترک هستند).

هنگام محاسبه توالی اصلی استورم توسط تقسیم اقلیدسی ، ممکن است اتفاق بیفتد که شخص با چند جمله ای روبرو شود که عاملی دارد که هرگز منفی نباشد ، چنین $x ^ {2$ یا $x ^ {2} +1$ . در این حالت ، اگر کسی محاسبات را با چند جمله ای که توسط فاکتور غیر منفی جایگزین آن شده است ، ادامه دهد ، یک دنبالهاستورم تعمیم داده می شود که ممکن است برای محاسبه تعداد ریشه های واقعی نیز استفاده شود ، زیرا اثبات قضیه Sturm هنوز هم اعمال می شود ( به دلیل شرط سوم). این ممکن است گاهی اوقات محاسبه را ساده کند ، اگرچه پیدا کردن چنین عواملی غیر منفی به استثنای قدرتهای x حتی معمولاً دشوار است .

استفاده از توالی های شبه باقیمانده [ ویرایش ]

در جبر رایانه ، چند جمله ای که در نظر گرفته می شود ضرایب عدد صحیح دارند یا ممکن است به ضرایب عدد صحیح تبدیل شوند. دنباله Sturm از چند جمله ای با ضرایب عدد صحیح ، عموماً شامل چند جمله ای است که ضرایب آن عدد صحیح نیستند (مثال بالا را ببینید).

برای جلوگیری از محاسبه با اعداد منطقی ، یک روش معمول جایگزینی تقسیم اقلیدسی توسط تقسیم شبه برای محاسبه بزرگترین تقسیم کننده های چند جمله ای است . این به معنای جایگزینی توالی باقیمانده الگوریتم اقلیدسی توسط یک دنباله شبه باقیمانده است ، یک دنباله شبه باقیمانده یک دنباله است. ${\ displaystyle p_ {0} ، \ ldots ، p_ {k}}$ از چند جمله ای به طوری که ثابت وجود دارد $a_ {من$ و $b_ {من$ به طوری که $\ displaystyle b_ {i} p_ {i + 1}}$ بخش باقیمانده بخش اقلیدسی است $display \ displaystyle a_ {i} p_ {i-1}}$ توسط ${\ displaystyle p_ {i}.}$ (انواع مختلف توالی های شبه باقیمانده با انتخاب گزینه ها تعریف می شوند $a_ {من$ و $\ displaystyle b_ {i}؛}$ معمولا، $a_ {من$ برای معرفی مخرج در طول تقسیم اقلیدسی انتخاب نشده است ، و $b_ {من$ یک تقسیم کننده مشترک ضرایب باقیمانده است. دیدن دنباله شبه باقی مانده برای جزئیات بیشتر.) به عنوان مثال، دنباله باقی مانده از الگوریتم اقلیدسی رشته شبه باقی مانده است $\ displaystyle a_ {i} = b_ {i} = 1$ برای هر من ، و دنباله استورم از چند جمله ای یک دنباله شبه باقیمانده با است ${\ displaystyle a_ {i} = 1$ و $\ displaystyle b_ {i} = - 1}$ برای هر من .

توالی های شبه باقیمانده مختلف برای محاسبه بزرگترین تقسیم کننده مشترک چند جمله ای با ضرایب عدد صحیح و بدون معرفی مخرج طراحی شده اند ( دنباله شبه باقیمانده را ببینید ). همه آنها را می توان با انتخاب علامت توالی استورم تعمیم داد $b_ {من$ برعکس نشانه $a_i$ این امکان استفاده از قضیه استورم را با توالی شبه باقی مانده فراهم می کند.

جداسازی ریشه [ ویرایش ]

برای چند جمله ای با ضرایب واقعی ، جداسازی ریشه شامل یافتن ، برای هر ریشه واقعی ، بازه ای است که شامل این ریشه است و هیچ ریشه دیگری ندارد.

این برای یافتن ریشه مفید است و امکان انتخاب ریشه فراهم می شود و نقطه شروع خوبی برای الگوریتم های عددی سریع مانند روش نیوتن است . همچنین برای تأیید نتیجه مفید است ، زیرا اگر روش نیوتن در خارج از فاصله زمانی همگرا شود ممکن است بلافاصله استنباط شود که به ریشه اشتباه همگرا می شود.

جداسازی ریشه برای محاسبه با اعداد جبری نیز مفید است . برای محاسبه با اعداد جبری ، یک روش معمول این است که آنها را به عنوان یک جفت چند جمله ای که عدد جبری یک ریشه است ، و یک فاصله انزوا نشان دهید. مثلا ${\ sqrt {2}$ ممکن است توسط ابهامات نمایان شود ${\ displaystyle (x ^ {2} -2 ، [0،2]).$

قضیه استورم راهی برای جداسازی ریشه های واقعی فراهم می کند که از کارایی کمتری (برای چند جمله ای ها با ضرایب عدد صحیح) نسبت به سایر روش های حاکم بر نشانه های دکارت برخوردار است . با این وجود ، در برخی شرایط ، عمدتاً برای مقاصد تئوری ، مفید است ، برای مثال برای الگوریتم های هندسه جبری واقعی که شامل نامتناهی ها است .

برای جداسازی ریشه های واقعی ، فرد از یک فاصله شروع می شود $(الف ، ب)$ حاوی تمام ریشه های واقعی ، یا ریشه های مورد علاقه (اغلب ، معمولاً در مشکلات جسمی ، فقط ریشه های مثبت جالب هستند) ، و یکی محاسبه می کند ${\ displaystyle V (a)$ و ${\ displaystyle V (b).$ برای تعریف این بازه شروع ، می توانید از اندازه ریشه ها استفاده کنید (به ویژگی های ریشه چند جمله ای: محدودیت های روی ریشه های چند جملهای (پیچیده) مراجعه کنید ). سپس ، با انتخاب c در وسط ، این فاصله را به دو قسمت تقسیم می کنیم ${\ displaystyle (a، b].$ محاسبه ${\ نمایشگر V (ج)}$ تعداد ریشه های واقعی را در ${\ نمایشگر (a، c]$ و ${\ نمایشگر (c ، b] ،$ و ممکن است یکی از عملیات های مشابه در هر زیر زیر تکرار شود. هنگامی که فرد مواجه می شود ، در طی این فرآیند فاصله ای که هیچ ریشه ای ندارد ، ممکن است از لیست فواصل مورد نظر سرکوب شود. هنگامی که یک فرد با فاصله ای دقیقاً یک ریشه روبرو می شود ، ممکن است فرد از تقسیم آن متوقف شود ، زیرا این یک فاصله ایزوله است. این فرآیند سرانجام متوقف می شود ، هنگامی که فقط فواصل ایزوله سازی باقی می ماند.

این فرایند جداسازی ممکن است با هر روشی برای محاسبه تعداد ریشه های واقعی در یک بازه استفاده شود. تجزیه و تحلیل پیچیدگی نظری و تجربیات عملی نشان می دهد که روش های مبتنی بر قانون علائم دکارت کارایی بیشتری دارند. از این رو نتیجه می گیرد که امروزه ، توالی استورم بندرت برای جداسازی ریشه استفاده می شود.

برنامه [ ویرایش ]

توالی استورم Generalized اجازه می دهد تا ریشه های چند جمله ای را که چند جمله ای دیگری نیز مثبت است (یا منفی) شمرده ، بدون محاسبه صریح این ریشه. اگر کسی فاصله ایزوله کننده برای ریشه اولین چند جملهای خود را بداند ، این امکان را می دهد تا بدون محاسبه تقریبی بهتر ریشه ، علامت چند جملهای دوم را نیز در این ریشه خاص چند جملهای اول پیدا کنید.

بگذارید( P ( x و (Q ( x دو چند جمله ای با ضرایب واقعی باشند به گونه ای که P و Q هیچ ریشه مشترکی ندارند و P دارای ریشه چندگانه نیست. به عبارت دیگر ، P و P ' Q چند جمله ای های coprime هستند . این محدودیت واقعاً بر کلی بودن آنچه در پی می آید تأثیر نمی گذارد ، زیرا محاسبات GCD اجازه می دهد تا پرونده کلی را برای این مورد کاهش دهیم ، و هزینه محاسبه یک دنبالهاستورم همان اندازه یک GCD است.

بگذارید W ( a ) تعداد تغییرات علامت را در یک توالی استورم تعمیم یافته با شروع از P و P ' Q مشخص کند . اگر a < b دو عدد واقعی باشد ، W ( a ) - W ( b ) تعداد ریشه های P در فاصله است $(الف ، ب)$ به گونه ای که Q ( a )> 0 منفی تعداد ریشه ها در همان فاصله است به گونه ای که Q ( a ) <0 . همراه با تعداد کل ریشه های P در همان بازه ای که با قضیه استورم داده شده است ، این تعداد ریشه های P را به گونه ای می دهد که Q ( a )> 0 و تعداد ریشه های P به گونه ای باشد که Q ( a ) <0 . [1]

حداکثر درجه P است .

منبع

https://en.wikipedia.org/wiki/Sturm%27s_theorem

قضیه استورم

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 22:47

در ریاضیات ، دنباله استورم از یک چند جمله ای p یک متغیره ، دنباله ای از چندجمله ای مرتبط با p و مشتق آن با یک نوع از الگوریتم اقلیدس برای چندجمله ای است . قضیه استورم بیان تعداد متمایز واقعی ریشه ازp واقع در یک فاصله زمانی از نظر تعدادی از تغییرات نشانه هایی از ارزش های دنباله استورم در مرزهای فاصله. با استفاده از فاصله همه اعداد واقعی ، تعداد کل ریشه های واقعی p را نشان می دهد . [1]
در حالی که قضیه اساسی جبر به راحتی تعداد کلی ریشه های پیچیده را که با کثرت شمارش می شود ، به دست می آورد ، روشی برای محاسبه آنها ارائه نمی دهد. قضیه استورم تعداد ریشه های واقعی متمایز را شمرده و آنها را در فواصل زمانی قرار می دهد. با تقسیم فواصل حاوی برخی از ریشه ها ، می توان ریشه ها را در فواصل کوچک دلخواه جدا کرد که هر یک دقیقاً یک ریشه دارد. این بازده قدیمی ترین الگوریتم جداسازی ریشه واقعی و الگوریتم دقیق یافتن ریشه برای چندجمله ای یک متغیره است.
برای محاسبه طول اعداد حقیقی ، قضیه استورم کارآمد کمتر از روش های دیگر بر اساس است حکومت دکارت از نشانه . با این حال ، آن را در هر زمینه بسته واقعی کار می کند ، و بنابراین ، برای مطالعه نظری پیچیدگی محاسباتی از تجزیه پذیری و حذف کمی در تئوری مرتبه اول اعداد واقعی اساسی است.
توالی استورم و قضیه استورم به نام ژاک چارلز فرانسوا استورم نامگذاری شده است که در سال 1829 قضیه را کشف کرد. [2]
فهرست1قضیه2مثال3تعمیم4استفاده از توالی های شبه باقیمانده5جداسازی ریشه6کاربرد7همچنین ببینید8منابعقضیه [ ویرایش ]
زنجیره استورم و یا توالی استورم یک چند جمله ای های تک متغیری( P ( X  با ضرایب حقیقی دنباله ای از چند جمله ای است به طوری که

برای من ≥ 1 ، که در آن P ' است مشتق از P ، وباقی مانده از است تقسیم اقلیدسی از توسططول دنباله
در ریاضیات ، دنباله استورم از یک چند جمله ای p یک متغیره ، دنباله ای از چندجمله ای مرتبط با p و مشتق آن با یک نوع از الگوریتم اقلیدس برای چندجمله ای است . قضیه استورم بیان تعداد متمایز واقعی ریشه ازp واقع در یک فاصله زمانی از نظر تعدادی از تغییرات نشانه هایی از ارزش های دنباله استورم در مرزهای فاصله. با استفاده از فاصله همه اعداد واقعی ، تعداد کل ریشه های واقعی p را نشان می دهد . [1]
در حالی که قضیه اساسی جبر به راحتی تعداد کلی ریشه های پیچیده را که با کثرت شمارش می شود ، به دست می آورد ، روشی برای محاسبه آنها ارائه نمی دهد. قضیه استورم تعداد ریشه های واقعی متمایز را شمرده و آنها را در فواصل زمانی قرار می دهد. با تقسیم فواصل حاوی برخی از ریشه ها ، می توان ریشه ها را در فواصل کوچک دلخواه جدا کرد که هر یک دقیقاً یک ریشه دارد. این بازده قدیمی ترین الگوریتم جداسازی ریشه واقعی و الگوریتم دقیق یافتن ریشه برای چندجملهای یک متغیره است.
برای محاسبه طول اعداد حقیقی ، قضیه استورم کارآمد کمتر از روش های دیگر بر اساس است حکومت دکارت از نشانه . با این حال ، آن را در هر زمینه بسته واقعی کار می کند ، و بنابراین ، برای مطالعه نظری پیچیدگی محاسباتی از تجزیه پذیری و حذف کمی در تئوری مرتبه اول اعداد واقعی اساسی است.
توالی استورم و قضیه استورم به نام ژاک چارلز فرانسوا استورم نامگذاری شده است که در سال 1829 قضیه را کشف کرد. [2]
فهرست1قضیه2مثال3تعمیم4استفاده از توالی های شبه باقیمانده5جداسازی ریشه6کاربرد7همچنین ببینید8منابعقضیه [ ویرایش ]
زنجیره استورم و یا توالی استورم یک چند جمله ای های تک متغیری  (P ( X با ضرایب حقیقی دنباله ای از چند جمله ای است به طوری که

برای من ≥ 1 ، که در آن P ' است مشتق از P ، وباقی مانده از است تقسیم اقلیدسی از توسططول دنباله Sturm حداکثر درجه P است .
تعداد تغییرات علامت در ξ دنباله Sturm از P تعداد تغییرات علامت-نادیده گرفتن صفرها در دنباله اعداد واقعی است

این تعداد از علائم در اینجا( V ( ξ مشخص شده است .
کشورهای قضیه استورم که اگر P است چند جمله ای رایگان مربع ، تعداد ریشه حقیقی متمایز از P در فاصله نیمه باز ( ، ب ] است   [1]
قضیه با تعیین علامت در + ∞ چند جمله ای به عنوان علامت ضریب پیشرو آن (به عنوان مثال ضریب اصطلاح بالاترین درجه) به فواصل نامحدود گسترش می یابد . در -∞ نشانه ای از یک چند جمله ای به نشانه ضریب پیشرو آن برای یک چند جمله ای حتی درجه، و علامت مخالف برای یک چندجملهای از درجه فرد است.
در مورد یک چند جمله ای غیر آزاد مربع، اگر نه و نه ب ریشه های متعدد از است p ، پس از آن V ( ) - V ( ب ) تعداد است متمایز ریشه های حقیقی P .
اثبات قضیه به شرح زیر است: وقتی مقدار x از a به b افزایش یابد ، ممکن است از صفر برخی عبور کند( i > 0 )؛ وقتی این اتفاق می افتد ، تعداد تغییرات علامت ازتغییر نمی کند. وقتی x از یک ریشه عبور می کند تعداد تغییرات علائم از 1 به 0 کاهش می یابد. این تنها مقادیر x است که ممکن است برخی از علائم تغییر کند.مثال [ ویرایش ]
فرض کنید ما می خواهیم تعداد ریشه ها را در چند دامنه برای چند جمله ای پیدا کنیم. بنابراین

باقی مانده از تقسیم اقلیدسی از p 0 توسط p 1 استضرب آن را با 1 پوند بدست می آوریم
.
تقسیم بعدی p 1 بر p 2 و ضرب باقیمانده توسط − 1 ، به دست می آوریم
.
اکنون p 2 را بر p 3 تقسیم می کنیم و باقیمانده را با − 1 ضرب می کنیم ، به دست می آوریم
.
از آنجا که این یک ثابت است ، این محاسبه محاسبات دنباله استورم را تمام می کند.
برای پیدا کردن تعداد ریشه های واقعی یکی به ارزیابی توالی از نشانه های این چند جمله ای در -∞ و ∞ ، که به ترتیب (+، -، +، +، -) و (+، +، +، -، -) . بدین ترتیب

که نشان می دهد p دارای دو ریشه واقعی است.
این امر را می توان با ذکر این نکته تأیید کرد که p ( x ) را می توان به عنوان ( x 2 - 1) ( x 2 + x + 1) تعیین کرد ، جایی که عامل اول دارای ریشه −1 و 1 است و فاکتور دوم ریشه واقعی ندارد. این آخرین ادعا از فرمول درجه دوم و همچنین از قضیه اشتورم حاصل می شود که توالی های علامت (+ ، - ، -) را در −∞ و (+ ، + ، -) در + gives به دست می دهد .تعمیم [ ویرایش ]
توالی Sturm از دو جهت تعمیم یافته است. برای تعریف هر چند جمله ای در دنباله ، Sturm از منفی باقی مانده تقسیم اقلیدسی دو مورد قبلی استفاده کرد. این قضیه صادق است اگر کسی منفی باقیمانده را توسط محصول یا مقدار آن با یک ثابت مثبت یا مربع چند جمله ای جایگزین کند. همچنین در نظر گرفتن سکانس هایی که چند جمله ای دوم مشتق اول نیست ، مفید است (در زیر مراجعه کنید).
توالی استورم تعمیم یک دنباله متناهی از چند جمله ای با ضرایب حقیقی است

به طوری کهدرجه بعد از درجه اول کاهش می یابد:برای i = 2 ، ... ، m ؛ هیچ ریشه واقعی ندارد و یا نشانه ای را در نزدیکی ریشه واقعی خود تغییر نمی دهد.اگر P i ( ξ ) = 0 برای 0 i m و ξ یک عدد واقعی باشد ، P P - 1 ( ξ ) P i + 1 ( ξ )
شرط آخر دلالت بر این دارد که دو چند جمله ای متوالی هیچ ریشه واقعی مشترکی ندارند. به طور خاص ، توالی اصلی استورم یک توالی استورم تعمیم یافته است ، اگر (و تنها در صورت این کار) چند جمله ای دارای ریشه واقعی چندگانه نیست (در غیر این صورت ، دو چند جمله ای اول دنباله استورم دارای یک ریشه مشترک هستند).
هنگام محاسبه توالی اصلی استورم توسط تقسیم اقلیدسی ، ممکن است اتفاق بیفتد که شخص با چند جمله ای روبرو شود که عاملی دارد که هرگز منفی نباشد ، چنین  یا. در این حالت ، اگر کسی محاسبات را با چند جمله ای که توسط فاکتور غیر منفی جایگزین آن شده است ، ادامه دهد ، یک دنبالهاستورم تعمیم داده می شود که ممکن است برای محاسبه تعداد ریشه های واقعی نیز استفاده شود ، زیرا اثبات قضیه Sturm هنوز هم اعمال می شود ( به دلیل شرط سوم). این ممکن است گاهی اوقات محاسبه را ساده کند ، اگرچه پیدا کردن چنین عواملی غیر منفی به استثنای قدرتهای x حتی معمولاً دشوار است .استفاده از توالی های شبه باقیمانده [ ویرایش ]
در جبر رایانه ، چند جمله ای که در نظر گرفته می شود ضرایب عدد صحیح دارند یا ممکن است به ضرایب عدد صحیح تبدیل شوند. دنباله Sturm از چند جمله ای با ضرایب عدد صحیح ، عموماً شامل چند جمله ای است که ضرایب آن عدد صحیح نیستند (مثال بالا را ببینید).
برای جلوگیری از محاسبه با اعداد منطقی ، یک روش معمول جایگزینی تقسیم اقلیدسی توسط تقسیم شبه برای محاسبه بزرگترین تقسیم کننده های چند جمله ای است . این به معنای جایگزینی توالی باقیمانده الگوریتم اقلیدسی توسط یک دنباله شبه باقیمانده است ، یک دنباله شبه باقیمانده یک دنباله است. از چند جمله ای به طوری که ثابت وجود دارد  و  به طوری که بخش باقیمانده بخش اقلیدسی است  توسط  (انواع مختلف توالی های شبه باقیمانده با انتخاب گزینه ها تعریف می شوند و  معمولا، برای معرفی مخرج در طول تقسیم اقلیدسی انتخاب نشده است ، و یک تقسیم کننده مشترک ضرایب باقیمانده است. دیدن دنباله شبه باقی مانده برای جزئیات بیشتر.) به عنوان مثال، دنباله باقی مانده از الگوریتم اقلیدسی رشته شبه باقی مانده استبرای هر من ، و دنباله استورم از چند جمله ای یک دنباله شبه باقیمانده با است و برای هر من .
توالی های شبه باقیمانده مختلف برای محاسبه بزرگترین تقسیم کننده مشترک چند جمله ای با ضرایب عدد صحیح و بدون معرفی مخرج طراحی شده اند ( دنباله شبه باقیمانده را ببینید ). همه آنها را می توان با انتخاب علامت توالی استورم تعمیم داد برعکس نشانه  این امکان استفاده از قضیه استورم را با توالی شبه باقی مانده فراهم می کند.جداسازی ریشه [ ویرایش ]
برای چند جمله ای با ضرایب واقعی ، جداسازی ریشه شامل یافتن ، برای هر ریشه واقعی ، بازه ای است که شامل این ریشه است و هیچ ریشه دیگری ندارد.
این برای یافتن ریشه مفید است و امکان انتخاب ریشه فراهم می شود و نقطه شروع خوبی برای الگوریتم های عددی سریع مانند روش نیوتن است . همچنین برای تأیید نتیجه مفید است ، زیرا اگر روش نیوتن در خارج از فاصله زمانی همگرا شود ممکن است بلافاصله استنباط شود که به ریشه اشتباه همگرا می شود.
جداسازی ریشه برای محاسبه با اعداد جبری نیز مفید است . برای محاسبه با اعداد جبری ، یک روش معمول این است که آنها را به عنوان یک جفت چند جمله ای که عدد جبری یک ریشه است ، و یک فاصله انزوا نشان دهید. مثلا ممکن است توسط ابهامات نمایان شود
قضیه استورم راهی برای جداسازی ریشه های واقعی فراهم می کند که از کارایی کمتری (برای چند جمله ای ها با ضرایب عدد صحیح) نسبت به سایر روش های حاکم بر نشانه های دکارت برخوردار است . با این وجود ، در برخی شرایط ، عمدتاً برای مقاصد تئوری ، مفید است ، برای مثال برای الگوریتم های هندسه جبری واقعی که شامل نامتناهی ها است .
برای جداسازی ریشه های واقعی ، فرد از یک فاصله شروع می شود  حاوی تمام ریشه های واقعی ، یا ریشه های مورد علاقه (اغلب ، معمولاً در مشکلات جسمی ، فقط ریشه های مثبت جالب هستند) ، و یکی محاسبه می کند  و برای تعریف این بازه شروع ، می توانید از اندازه ریشه ها استفاده کنید (به ویژگی های ریشه چند جمله ای: محدودیت های روی ریشه های چند جملهای (پیچیده) مراجعه کنید ). سپس ، با انتخاب c در وسط ، این فاصله را به دو قسمت تقسیم می کنیم محاسبه  تعداد ریشه های واقعی را در  و و ممکن است یکی از عملیات های مشابه در هر زیر زیر تکرار شود. هنگامی که فرد مواجه می شود ، در طی این فرآیند فاصله ای که هیچ ریشه ای ندارد ، ممکن است از لیست فواصل مورد نظر سرکوب شود. هنگامی که یک فرد با فاصله ای دقیقاً یک ریشه روبرو می شود ، ممکن است فرد از تقسیم آن متوقف شود ، زیرا این یک فاصله ایزوله است. این فرآیند سرانجام متوقف می شود ، هنگامی که فقط فواصل ایزوله سازی باقی می ماند.
این فرایند جداسازی ممکن است با هر روشی برای محاسبه تعداد ریشه های واقعی در یک بازه استفاده شود. تجزیه و تحلیل پیچیدگی نظری و تجربیات عملی نشان می دهد که روش های مبتنی بر قانون علائم دکارت کارایی بیشتری دارند. از این رو نتیجه می گیرد که امروزه ، توالی استورم بندرت برای جداسازی ریشه استفاده می شود.برنامه [ ویرایش ]
توالی استورم Generalized اجازه می دهد تا ریشه های چند جمله ای را که چند جمله ای دیگری نیز مثبت است (یا منفی) شمرده ، بدون محاسبه صریح این ریشه. اگر کسی فاصله ایزوله کننده برای ریشه اولین چند جملهای خود را بداند ، این امکان را می دهد تا بدون محاسبه تقریبی بهتر ریشه ، علامت چند جملهای دوم را نیز در این ریشه خاص چند جملهای اول پیدا کنید.
بگذارید( P ( x  و (Q ( x  دو چند جمله ای با ضرایب واقعی باشند به گونه ای که P و Q هیچ ریشه مشترکی ندارند و P دارای ریشه چندگانه نیست. به عبارت دیگر ، P و P ' Q چند جمله ای های coprime هستند . این محدودیت واقعاً بر کلی بودن آنچه در پی می آید تأثیر نمی گذارد ، زیرا محاسبات GCD اجازه می دهد تا پرونده کلی را برای این مورد کاهش دهیم ، و هزینه محاسبه یک دنبالهاستورم همان اندازه یک GCD است.
بگذارید W ( a ) تعداد تغییرات علامت را در یک توالی استورم تعمیم یافته با شروع از P و P ' Q مشخص کند . اگر a b دو عدد واقعی باشد ، W ( a ) - W ( b ) تعداد ریشه های P در فاصله استبه گونه ای که Q ( a )> 0 منفی تعداد ریشه ها در همان فاصله است به گونه ای که Q ( a ) P در همان بازه ای که با قضیه استورم داده شده است ، این تعداد ریشه های P را به گونه ای می دهد که Q ( a )> 0 و تعداد ریشه های P به گونه ای باشد که Q ( a ) [1]
حداکثر درجه P است .
تعداد تغییرات علامت در ξ دنباله
در ریاضیات ، دنباله استورم از یک چند جمله ای p یک متغیره ، دنباله ای از چندجملهای مرتبط با p و مشتق آن با یک نوع از الگوریتم اقلیدس برای چندجملهای است . قضیه استورم بیان تعداد متمایز واقعی ریشه ازp واقع در یک فاصله زمانی از نظر تعدادی از تغییرات نشانه هایی از ارزش های دنباله استورم در مرزهای فاصله. با استفاده از فاصله همه اعداد واقعی ، تعداد کل ریشه های واقعی p را نشان می دهد . [1]
در حالی که قضیه اساسی جبر به راحتی تعداد کلی ریشه های پیچیده را که با کثرت شمارش می شود ، به دست می آورد ، روشی برای محاسبه آنها ارائه نمی دهد. قضیه استورم تعداد ریشه های واقعی متمایز را شمرده و آنها را در فواصل زمانی قرار می دهد. با تقسیم فواصل حاوی برخی از ریشه ها ، می توان ریشه ها را در فواصل کوچک دلخواه جدا کرد که هر یک دقیقاً یک ریشه دارد. این بازده قدیمی ترین الگوریتم جداسازی ریشه واقعی و الگوریتم دقیق یافتن ریشه برای چندجملهای یک متغیره است.
برای محاسبه طول اعداد حقیقی ، قضیه استورم کارآمد کمتر از روش های دیگر بر اساس است حکومت دکارت از نشانه . با این حال ، آن را در هر زمینه بسته واقعی کار می کند ، و بنابراین ، برای مطالعه نظری پیچیدگی محاسباتی از تجزیه پذیری و حذف کمی در تئوری مرتبه اول اعداد واقعی اساسی است.
توالی استورم و قضیه استورم به نام ژاک چارلز فرانسوا استورم نامگذاری شده است که در سال 1829 قضیه را کشف کرد. [2]
فهرست1قضیه2مثال3تعمیم4استفاده از توالی های شبه باقیمانده5جداسازی ریشه6کاربرد7همچنین ببینید8منابعقضیه [ ویرایش ]
زنجیره استورم و یا توالی استورم یک چند جمله ای های تک متغیری P ( X ) با ضرایب حقیقی دنباله ای از چند جمله ای است به طوری که

برای من ≥ 1 ، که در آن P ' است مشتق از P ، وباقی مانده از است تقسیم اقلیدسی از توسططول دنباله Sturm حداکثر درجه P است .
تعداد تغییرات علامت در ξ دنباله Sturm از P تعداد تغییرات علامت-نادیده گرفتن صفرها در دنباله اعداد واقعی است

این تعداد از علائم در اینجا( V ( ξ مشخص شده است .
کشورهای قضیه استورم که اگر P است چند جمله ای رایگان مربع ، تعداد ریشه حقیقی متمایز از P در فاصله نیمه باز ( ، ب ] است V ( ) - V ( ب ) (در اینجا، و ب هستند اعداد واقعی به گونه ای که یک b ). [1]
قضیه با تعیین علامت در + ∞ چند جمله ای به عنوان علامت ضریب پیشرو آن (به عنوان مثال ضریب اصطلاح بالاترین درجه) به فواصل نامحدود گسترش می یابد . در -∞ نشانه ای از یک چند جمله ای به نشانه ضریب پیشرو آن برای یک چند جمله ای حتی درجه، و علامت مخالف برای یک چندجملهای از درجه فرد است.
در مورد یک چند جمله ای غیر آزاد مربع، اگر نه و نه ب ریشه های متعدد از است p ، پس از آن V ( ) - V ( ب ) تعداد است متمایز ریشه های حقیقی P .
اثبات قضیه به شرح زیر است: وقتی مقدار x از a به b افزایش یابد ، ممکن است از صفر برخی عبور کند( i > 0 )؛ وقتی این اتفاق می افتد ، تعداد تغییرات علامت ازتغییر نمی کند. وقتی x از یک ریشه عبور می کند تعداد تغییرات علائم از 1 به 0 کاهش می یابد. این تنها مقادیر x است که ممکن است برخی از علائم تغییر کند.مثال [ ویرایش ]
فرض کنید ما می خواهیم تعداد ریشه ها را در چند دامنه برای چند جمله ای پیدا کنیم. بنابراین

باقی مانده از تقسیم اقلیدسی از p 0 توسط p 1 استضرب آن را با 1 پوند بدست می آوریم
.
تقسیم بعدی p 1 بر p 2 و ضرب باقیمانده توسط − 1 ، به دست می آوریم
.
اکنون p 2 را بر p 3 تقسیم می کنیم و باقیمانده را با − 1 ضرب می کنیم ، به دست می آوریم
.
از آنجا که این یک ثابت است ، این محاسبه محاسبات دنباله استورم را تمام می کند.
برای پیدا کردن تعداد ریشه های واقعی یکی به ارزیابی توالی از نشانه های این چند جمله ای در -∞ و ∞ ، که به ترتیب (+، -، +، +، -) و (+، +، +، -، -) . بدین ترتیب

که نشان می دهد p دارای دو ریشه واقعی است.
این امر را می توان با ذکر این نکته تأیید کرد که p ( x ) را می توان به عنوان ( x 2 - 1) ( x 2 + x + 1) تعیین کرد ، جایی که عامل اول دارای ریشه −1 و 1 است و فاکتور دوم ریشه واقعی ندارد. این آخرین ادعا از فرمول درجه دوم و همچنین از قضیه اشتورم حاصل می شود که توالی های علامت (+ ، - ، -) را در −∞ و (+ ، + ، -) در + gives به دست می دهد .تعمیم [ ویرایش ]
توالی Sturm از دو جهت تعمیم یافته است. برای تعریف هر چند جمله ای در دنباله ، Sturm از منفی باقی مانده تقسیم اقلیدسی دو مورد قبلی استفاده کرد. این قضیه صادق است اگر کسی منفی باقیمانده را توسط محصول یا مقدار آن با یک ثابت مثبت یا مربع چند جمله ای جایگزین کند. همچنین در نظر گرفتن سکانس هایی که چند جمله ای دوم مشتق اول نیست ، مفید است (در زیر مراجعه کنید).
توالی استورم تعمیم یک دنباله متناهی از چند جمله ای با ضرایب حقیقی است

به طوری کهدرجه بعد از درجه اول کاهش می یابد:برای i = 2 ، ... ، m ؛ هیچ ریشه واقعی ندارد و یا نشانه ای را در نزدیکی ریشه واقعی خود تغییر نمی دهد.اگر P i ( ξ ) = 0 برای 0 i m و ξ یک عدد واقعی باشد ، P P - 1 ( ξ ) P i + 1 ( ξ )
شرط آخر دلالت بر این دارد که دو چند جمله ای متوالی هیچ ریشه واقعی مشترکی ندارند. به طور خاص ، توالی اصلی استورم یک توالی استورم تعمیم یافته است ، اگر (و تنها در صورت این کار) چند جمله ای دارای ریشه واقعی چندگانه نیست (در غیر این صورت ، دو چند جمله ای اول دنباله استورم دارای یک ریشه مشترک هستند).
هنگام محاسبه توالی اصلی استورم توسط تقسیم اقلیدسی ، ممکن است اتفاق بیفتد که شخص با چند جمله ای روبرو شود که عاملی دارد که هرگز منفی نباشد ، چنین  یا. در این حالت ، اگر کسی محاسبات را با چند جمله ای که توسط فاکتور غیر منفی جایگزین آن شده است ، ادامه دهد ، یک دنبالهاستورم تعمیم داده می شود که ممکن است برای محاسبه تعداد ریشه های واقعی نیز استفاده شود ، زیرا اثبات قضیه Sturm هنوز هم اعمال می شود ( به دلیل شرط سوم). این ممکن است گاهی اوقات محاسبه را ساده کند ، اگرچه پیدا کردن چنین عواملی غیر منفی به استثنای قدرتهای x حتی معمولاً دشوار است .استفاده از توالی های شبه باقیمانده [ ویرایش ]
در جبر رایانه ، چند جمله ای که در نظر گرفته می شود ضرایب عدد صحیح دارند یا ممکن است به ضرایب عدد صحیح تبدیل شوند. دنباله Sturm از چند جمله ای با ضرایب عدد صحیح ، عموماً شامل چند جمله ای است که ضرایب آن عدد صحیح نیستند (مثال بالا را ببینید).
برای جلوگیری از محاسبه با اعداد منطقی ، یک روش معمول جایگزینی تقسیم اقلیدسی توسط تقسیم شبه برای محاسبه بزرگترین تقسیم کننده های چند جمله ای است . این به معنای جایگزینی توالی باقیمانده الگوریتم اقلیدسی توسط یک دنباله شبه باقیمانده است ، یک دنباله شبه باقیمانده یک دنباله است. از چند جمله ای به طوری که ثابت وجود دارد  و  به طوری که بخش باقیمانده بخش اقلیدسی است  توسط  (انواع مختلف توالی های شبه باقیمانده با انتخاب گزینه ها تعریف می شوند و  معمولا، برای معرفی مخرج در طول تقسیم اقلیدسی انتخاب نشده است ، و یک تقسیم کننده مشترک ضرایب باقیمانده است. دیدن دنباله شبه باقی مانده برای جزئیات بیشتر.) به عنوان مثال، دنباله باقی مانده از الگوریتم اقلیدسی رشته شبه باقی مانده استبرای هر من ، و دنباله استورم از چند جمله ای یک دنباله شبه باقیمانده با است و برای هر من .
توالی های شبه باقیمانده مختلف برای محاسبه بزرگترین تقسیم کننده مشترک چند جمله ای با ضرایب عدد صحیح و بدون معرفی مخرج طراحی شده اند ( دنباله شبه باقیمانده را ببینید ). همه آنها را می توان با انتخاب علامت توالی استورم تعمیم داد برعکس نشانه  این امکان استفاده از قضیه استورم را با توالی شبه باقی مانده فراهم می کند.جداسازی ریشه [ ویرایش ]
برای چند جمله ای با ضرایب واقعی ، جداسازی ریشه شامل یافتن ، برای هر ریشه واقعی ، بازه ای است که شامل این ریشه است و هیچ ریشه دیگری ندارد.
این برای یافتن ریشه مفید است و امکان انتخاب ریشه فراهم می شود و نقطه شروع خوبی برای الگوریتم های عددی سریع مانند روش نیوتن است . همچنین برای تأیید نتیجه مفید است ، زیرا اگر روش نیوتن در خارج از فاصله زمانی همگرا شود ممکن است بلافاصله استنباط شود که به ریشه اشتباه همگرا می شود.
جداسازی ریشه برای محاسبه با اعداد جبری نیز مفید است . برای محاسبه با اعداد جبری ، یک روش معمول این است که آنها را به عنوان یک جفت چند جمله ای که عدد جبری یک ریشه است ، و یک فاصله انزوا نشان دهید. مثلا ممکن است توسط ابهامات نمایان شود
قضیه استورم راهی برای جداسازی ریشه های واقعی فراهم می کند که از کارایی کمتری (برای چند جمله ای ها با ضرایب عدد صحیح) نسبت به سایر روش های حاکم بر نشانه های دکارت برخوردار است . با این وجود ، در برخی شرایط ، عمدتاً برای مقاصد تئوری ، مفید است ، برای مثال برای الگوریتم های هندسه جبری واقعی که شامل نامتناهی ها است .
برای جداسازی ریشه های واقعی ، فرد از یک فاصله شروع می شود  حاوی تمام ریشه های واقعی ، یا ریشه های مورد علاقه (اغلب ، معمولاً در مشکلات جسمی ، فقط ریشه های مثبت جالب هستند) ، و یکی محاسبه می کند  و برای تعریف این بازه شروع ، می توانید از اندازه ریشه ها استفاده کنید (به ویژگی های ریشه چند جمله ای: محدودیت های روی ریشه های چند جملهای (پیچیده) مراجعه کنید ). سپس ، با انتخاب c در وسط ، این فاصله را به دو قسمت تقسیم می کنیم محاسبه  تعداد ریشه های واقعی را در  و و ممکن است یکی از عملیات های مشابه در هر زیر زیر تکرار شود. هنگامی که فرد مواجه می شود ، در طی این فرآیند فاصله ای که هیچ ریشه ای ندارد ، ممکن است از لیست فواصل مورد نظر سرکوب شود. هنگامی که یک فرد با فاصله ای دقیقاً یک ریشه روبرو می شود ، ممکن است فرد از تقسیم آن متوقف شود ، زیرا این یک فاصله ایزوله است. این فرآیند سرانجام متوقف می شود ، هنگامی که فقط فواصل ایزوله سازی باقی می ماند.
این فرایند جداسازی ممکن است با هر روشی برای محاسبه تعداد ریشه های واقعی در یک بازه استفاده شود. تجزیه و تحلیل پیچیدگی نظری و تجربیات عملی نشان می دهد که روش های مبتنی بر قانون علائم دکارت کارایی بیشتری دارند. از این رو نتیجه می گیرد که امروزه ، توالی استورم بندرت برای جداسازی ریشه استفاده می شود.برنامه [ ویرایش ]
توالی استورم Generalized اجازه می دهد تا ریشه های چند جمله ای را که چند جمله ای دیگری نیز مثبت است (یا منفی) شمرده ، بدون محاسبه صریح این ریشه. اگر کسی فاصله ایزوله کننده برای ریشه اولین چند جملهای خود را بداند ، این امکان را می دهد تا بدون محاسبه تقریبی بهتر ریشه ، علامت چند جملهای دوم را نیز در این ریشه خاص چند جملهای اول پیدا کنید.
بگذارید( P ( x  و (Q ( x  دو چند جمله ای با ضرایب واقعی باشند به گونه ای که P و Q هیچ ریشه مشترکی ندارند و P دارای ریشه چندگانه نیست. به عبارت دیگر ، P و P ' Q چند جمله ای های coprime هستند . این محدودیت واقعاً بر کلی بودن آنچه در پی می آید تأثیر نمی گذارد ، زیرا محاسبات GCD اجازه می دهد تا پرونده کلی را برای این مورد کاهش دهیم ، و هزینه محاسبه یک دنبالهاستورم همان اندازه یک GCD است.
بگذارید W ( a ) تعداد تغییرات علامت را در یک توالی استورم تعمیم یافته با شروع از P و P ' Q مشخص کند . اگر a b دو عدد واقعی باشد ، W ( a ) - W ( b ) تعداد ریشه های P در فاصله استبه گونه ای که Q ( a )> 0 منفی تعداد ریشه ها در همان فاصله است به گونه ای که Q ( a ) P در همان بازه ای که با قضیه استورم داده شده است ، این تعداد ریشه های P را به گونه ای می دهد که Q ( a )> 0 و تعداد ریشه های P به گونه ای باشد که Q ( a ) [1]
منبع
https://en.wikipedia.org/wiki/Sturm%27s_theorem
از P تعداد تغییرات علامت-نادیده گرفتن صفرها در دنباله اعداد واقعی است

این تعداد از علائم در اینجا( V ( ξ مشخص شده است .
کشورهای قضیه استورم که اگر P است چند جمله ای رایگان مربع ، تعداد ریشه حقیقی متمایز از P در فاصله نیمه باز ( ، ب ] است V ( ) - V ( ب ) (در اینجا، و ب هستند اعداد واقعی به گونه ای که یک b ). [1]
قضیه با تعیین علامت در + ∞ چند جمله ای به عنوان علامت ضریب پیشرو آن (به عنوان مثال ضریب اصطلاح بالاترین درجه) به فواصل نامحدود گسترش می یابد . در -∞ نشانه ای از یک چند جمله ای به نشانه ضریب پیشرو آن برای یک چند جمله ای حتی درجه، و علامت مخالف برای یک چندجملهای از درجه فرد است.
در مورد یک چند جمله ای غیر آزاد مربع، اگر نه و نه ب ریشه های متعدد از است p ، پس از آن V ( ) - V ( ب ) تعداد است متمایز ریشه های حقیقی P .
اثبات قضیه به شرح زیر است: وقتی مقدار x از a به b افزایش یابد ، ممکن است از صفر برخی عبور کند( i > 0 )؛ وقتی این اتفاق می افتد ، تعداد تغییرات علامت ازتغییر نمی کند. وقتی x از یک ریشه عبور می کند تعداد تغییرات علائم از 1 به 0 کاهش می یابد. این تنها مقادیر x است که ممکن است برخی از علائم تغییر کند.مثال [ ویرایش ]
فرض کنید ما می خواهیم تعداد ریشه ها را در چند دامنه برای چند جمله ای پیدا کنیم. بنابراین

باقی مانده از تقسیم اقلیدسی از p 0 توسط p 1 استضرب آن را با 1 پوند بدست می آوریم
.
تقسیم بعدی p 1 بر p 2 و ضرب باقیمانده توسط − 1 ، به دست می آوریم
.
اکنون p 2 را بر p 3 تقسیم می کنیم و باقیمانده را با − 1 ضرب می کنیم ، به دست می آوریم
.
از آنجا که این یک ثابت است ، این محاسبه محاسبات دنباله استورم را تمام می کند.
برای پیدا کردن تعداد ریشه های واقعی یکی به ارزیابی توالی از نشانه های این چند جمله ای در -∞ و ∞ ، که به ترتیب (+، -، +، +، -) و (+، +، +، -، -) . بدین ترتیب

که نشان می دهد p دارای دو ریشه واقعی است.
این امر را می توان با ذکر این نکته تأیید کرد که p ( x ) را می توان به عنوان ( x 2 - 1) ( x 2 + x + 1) تعیین کرد ، جایی که عامل اول دارای ریشه −1 و 1 است و فاکتور دوم ریشه واقعی ندارد. این آخرین ادعا از فرمول درجه دوم و همچنین از قضیه اشتورم حاصل می شود که توالی های علامت (+ ، - ، -) را در −∞ و (+ ، + ، -) در + gives به دست می دهد .تعمیم [ ویرایش ]
توالی Sturm از دو جهت تعمیم یافته است. برای تعریف هر چند جمله ای در دنباله ، Sturm از منفی باقی مانده تقسیم اقلیدسی دو مورد قبلی استفاده کرد. این قضیه صادق است اگر کسی منفی باقیمانده را توسط محصول یا مقدار آن با یک ثابت مثبت یا مربع چند جمله ای جایگزین کند. همچنین در نظر گرفتن سکانس هایی که چند جمله ای دوم مشتق اول نیست ، مفید است (در زیر مراجعه کنید).
توالی استورم تعمیم یک دنباله متناهی از چند جمله ای با ضرایب حقیقی است

به طوری کهدرجه بعد از درجه اول کاهش می یابد:برای i = 2 ، ... ، m ؛ هیچ ریشه واقعی ندارد و یا نشانه ای را در نزدیکی ریشه واقعی خود تغییر نمی دهد.اگر P i ( ξ ) = 0 برای 0 i m و ξ یک عدد واقعی باشد ، P P - 1 ( ξ ) P i + 1 ( ξ ) .
شرط آخر دلالت بر این دارد که دو چند جمله ای متوالی هیچ ریشه واقعی مشترکی ندارند. به طور خاص ، توالی اصلی استورم یک توالی استورم تعمیم یافته است ، اگر (و تنها در صورت این کار) چند جمله ای دارای ریشه واقعی چندگانه نیست (در غیر این صورت ، دو چند جمله ای اول دنباله استورم دارای یک ریشه مشترک هستند).
هنگام محاسبه توالی اصلی استورم توسط تقسیم اقلیدسی ، ممکن است اتفاق بیفتد که شخص با چند جمله ای روبرو شود که عاملی دارد که هرگز منفی نباشد ، چنین  یا. در این حالت ، اگر کسی محاسبات را با چند جمله ای که توسط فاکتور غیر منفی جایگزین آن شده است ، ادامه دهد ، یک دنبالهاستورم تعمیم داده می شود که ممکن است برای محاسبه تعداد ریشه های واقعی نیز استفاده شود ، زیرا اثبات قضیه Sturm هنوز هم اعمال می شود ( به دلیل شرط سوم). این ممکن است گاهی اوقات محاسبه را ساده کند ، اگرچه پیدا کردن چنین عواملی غیر منفی به استثنای قدرتهای x حتی معمولاً دشوار است .استفاده از توالی های شبه باقیمانده [ ویرایش ]
در جبر رایانه ، چند جمله ای که در نظر گرفته می شود ضرایب عدد صحیح دارند یا ممکن است به ضرایب عدد صحیح تبدیل شوند. دنباله Sturm از چند جمله ای با ضرایب عدد صحیح ، عموماً شامل چند جمله ای است که ضرایب آن عدد صحیح نیستند (مثال بالا را ببینید).
برای جلوگیری از محاسبه با اعداد منطقی ، یک روش معمول جایگزینی تقسیم اقلیدسی توسط تقسیم شبه برای محاسبه بزرگترین تقسیم کننده های چند جمله ای است . این به معنای جایگزینی توالی باقیمانده الگوریتم اقلیدسی توسط یک دنباله شبه باقیمانده است ، یک دنباله شبه باقیمانده یک دنباله است. از چند جمله ای به طوری که ثابت وجود دارد  و  به طوری که بخش باقیمانده بخش اقلیدسی است  توسط  (انواع مختلف توالی های شبه باقیمانده با انتخاب گزینه ها تعریف می شوند و  معمولا، برای معرفی مخرج در طول تقسیم اقلیدسی انتخاب نشده است ، و یک تقسیم کننده مشترک ضرایب باقیمانده است. دیدن دنباله شبه باقی مانده برای جزئیات بیشتر.) به عنوان مثال، دنباله باقی مانده از الگوریتم اقلیدسی رشته شبه باقی مانده استبرای هر من ، و دنباله استورم از چند جمله ای یک دنباله شبه باقیمانده با است و برای هر من .
توالی های شبه باقیمانده مختلف برای محاسبه بزرگترین تقسیم کننده مشترک چند جمله ای با ضرایب عدد صحیح و بدون معرفی مخرج طراحی شده اند ( دنباله شبه باقیمانده را ببینید ). همه آنها را می توان با انتخاب علامت توالی استورم تعمیم داد برعکس نشانه  این امکان استفاده از قضیه استورم را با توالی شبه باقی مانده فراهم می کند.جداسازی ریشه [ ویرایش ]
برای چند جمله ای با ضرایب واقعی ، جداسازی ریشه شامل یافتن ، برای هر ریشه واقعی ، بازه ای است که شامل این ریشه است و هیچ ریشه دیگری ندارد.
این برای یافتن ریشه مفید است و امکان انتخاب ریشه فراهم می شود و نقطه شروع خوبی برای الگوریتم های عددی سریع مانند روش نیوتن است . همچنین برای تأیید نتیجه مفید است ، زیرا اگر روش نیوتن در خارج از فاصله زمانی همگرا شود ممکن است بلافاصله استنباط شود که به ریشه اشتباه همگرا می شود.
جداسازی ریشه برای محاسبه با اعداد جبری نیز مفید است . برای محاسبه با اعداد جبری ، یک روش معمول این است که آنها را به عنوان یک جفت چند جمله ای که عدد جبری یک ریشه است ، و یک فاصله انزوا نشان دهید. مثلا ممکن است توسط ابهامات نمایان شود
قضیه استورم راهی برای جداسازی ریشه های واقعی فراهم می کند که از کارایی کمتری (برای چند جمله ای ها با ضرایب عدد صحیح) نسبت به سایر روش های حاکم بر نشانه های دکارت برخوردار است . با این وجود ، در برخی شرایط ، عمدتاً برای مقاصد تئوری ، مفید است ، برای مثال برای الگوریتم های هندسه جبری واقعی که شامل نامتناهی ها است .
برای جداسازی ریشه های واقعی ، فرد از یک فاصله شروع می شود  حاوی تمام ریشه های واقعی ، یا ریشه های مورد علاقه (اغلب ، معمولاً در مشکلات جسمی ، فقط ریشه های مثبت جالب هستند) ، و یکی محاسبه می کند  و برای تعریف این بازه شروع ، می توانید از اندازه ریشه ها استفاده کنید (به ویژگی های ریشه چند جمله ای: محدودیت های روی ریشه های چند جملهای (پیچیده) مراجعه کنید ). سپس ، با انتخاب c در وسط ، این فاصله را به دو قسمت تقسیم می کنیم محاسبه  تعداد ریشه های واقعی را در  و و ممکن است یکی از عملیات های مشابه در هر زیر زیر تکرار شود. هنگامی که فرد مواجه می شود ، در طی این فرآیند فاصله ای که هیچ ریشه ای ندارد ، ممکن است از لیست فواصل مورد نظر سرکوب شود. هنگامی که یک فرد با فاصله ای دقیقاً یک ریشه روبرو می شود ، ممکن است فرد از تقسیم آن متوقف شود ، زیرا این یک فاصله ایزوله است. این فرآیند سرانجام متوقف می شود ، هنگامی که فقط فواصل ایزوله سازی باقی می ماند.
این فرایند جداسازی ممکن است با هر روشی برای محاسبه تعداد ریشه های واقعی در یک بازه استفاده شود. تجزیه و تحلیل پیچیدگی نظری و تجربیات عملی نشان می دهد که روش های مبتنی بر قانون علائم دکارت کارایی بیشتری دارند. از این رو نتیجه می گیرد که امروزه ، توالی استورم بندرت برای جداسازی ریشه استفاده می شود.برنامه [ ویرایش ]
توالی استورم Generalized اجازه می دهد تا ریشه های چند جمله ای را که چند جمله ای دیگری نیز مثبت است (یا منفی) شمرده ، بدون محاسبه صریح این ریشه. اگر کسی فاصله ایزوله کننده برای ریشه اولین چند جملهای خود را بداند ، این امکان را می دهد تا بدون محاسبه تقریبی بهتر ریشه ، علامت چند جملهای دوم را نیز در این ریشه خاص چند جملهای اول پیدا کنید.
بگذارید( P ( x  و (Q ( x  دو چند جمله ای با ضرایب واقعی باشند به گونه ای که P و Q هیچ ریشه مشترکی ندارند و P دارای ریشه چندگانه نیست. به عبارت دیگر ، P و P ' Q چند جمله ای های coprime هستند . این محدودیت واقعاً بر کلی بودن آنچه در پی می آید تأثیر نمی گذارد ، زیرا محاسبات GCD اجازه می دهد تا پرونده کلی را برای این مورد کاهش دهیم ، و هزینه محاسبه یک دنبالهاستورم همان اندازه یک GCD است.
بگذارید W ( a ) تعداد تغییرات علامت را در یک توالی استورم تعمیم یافته با شروع از P و P ' Q مشخص کند . اگر a b دو عدد واقعی باشد ، W ( a ) - W ( b ) تعداد ریشه های P در فاصله استبه گونه ای که Q ( a )> 0 منفی تعداد ریشه ها در همان فاصله است به گونه ای که Q ( a ) . همراه با تعداد کل ریشه های P در همان بازه ای که با قضیه استورم داده شده است ، این تعداد ریشه های P را به گونه ای می دهد که Q ( a )> 0 و تعداد ریشه های P به گونه ای باشد که Q ( a ) . [1]
منبع
https://en.wikipedia.org/wiki/Sturm%27s_theorem

نظریه نوسان

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 22:32

در ریاضیات ، در زمینه معادلات دیفرانسیل معمولی ، یک راه حل غیر اصلی برای معادله دیفرانسیل معمولی

$F (x، y، y '، \ \ dot، \ y ^ {{(n-1)}}) = y ^ {{(n) qu \ quad x \ in [0، + \ infty)$

اگر تعداد نامتناهی ریشه داشته باشد ، نوسان کننده نامیده می شود . در غیر این صورت آن را غیر نوسان می گویند . معادله دیفرانسیل است که به نام نوسان اگر آن را تا یک راه حل نوسان. تعداد ریشه ها همچنین اطلاعاتی در مورد طیف مشکلات ارزش مرزی مرتبط دارد .

فهرست

مثالها [ ویرایش ]

معادله دیفرانسیل

${\ displaystyle y '' + y = 0$

نوسان است زیرا گناه ( x ) یک راه حل است.

ارتباط با تئوری طیفی [ ویرایش ]

تئوری نوسانات توسط ژاک چارلز فرانسوا استورم در تحقیقات خود درباره مشکلات اشتورم-لیوویل از سال 1836 آغاز شد. در آنجا وی نشان داد که عملکرد عملکردی یکم از مسئله اشتورم-لیوویل دقیقاً دارای ریشه 1 است. برای معادله یک بعدی شرودینگر سؤال در مورد نوسان / عدم نوسان به این سؤال پاسخ می دهد که آیا مقادیر ویژه در انتهای طیف مداوم جمع می شوند یا خیر.

نظریه نوسانات نسبی [ ویرایش ]

در سال 1996 Gesztesy - Simon - Teschl نشان داد که تعداد ریشه های تعیین کننده Wronski از دو عملکرد ویژه ی یک مشکل Sturm-Liouville به تعدادی از مقادیر ویژه ای بین مقادیر ویژه مربوطه می دهد. بعداً توسط Krüger-Teschl به مورد دو عامل اساسی در مورد دو مشکل مختلف Sturm-Liouville تعمیم داده شد. بررسی تعداد ریشه های تعیین کننده Wronski از دو راه حل به عنوان نظریه نوسان نسبی شناخته شده است.

منبع

https://en.wikipedia.org/wiki/Oscillation_theory

ادامه نظریه اشتورم-لیوویل

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 22:28

کاربرد معادلات دیفرانسیل جزئی [ ویرایش ]

حالتهای عادی [ ویرایش ]

برخی از معادلات دیفرانسیل جزئی با کمک تئوری SL قابل حل هستند. فرض کنید ما به حالت های ارتعاشی یک غشای نازک ، که در یک قاب مستطیل شکل برگزار می شود ، 0 ≤ x ≤ L 1 ، 0 ≤ y ≤ L 2 علاقه مند هستیم . معادله حرکت برای جابجایی غشای عمودی ، W ( x ، y ، t ) توسط معادله موج داده شده است :

$\ displaystyle {\ frac {\ partial ^ {2} W} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} W} {\ جزئی y ^ {2}}} = { \ frac {1} {c ^ {2}}} {\ frac {\ جزئی ^ {2} W} {\ جزئی t ^ {2}}}.$

روش جداسازی متغیرها پیشنهاد می کند که ابتدا به دنبال راه حلهای فرم ساده W = X ( x ) × Y ( y ) × T ( t ) باشید . برای چنین عملکردی W معادله دیفرانسیل جزئی تبدیل می شودX ″/ایکس + Y "/Y = 1/ج 2 T ″/تی. از آنجا که سه اصطلاح این معادله توابع x ، y ، t به طور جداگانه است ، آنها باید ثابت باشند. به عنوان مثال ، اصطلاح اول X X = λX را برای λ ثابت ثابت می دهد . شرایط مرزی ("در یک قاب مستطیل شکل") در صورت x = 0 ، L 1 یا y = 0 ، L 2 W = 0 می باشد و ساده ترین مشکلات ویژه مقادیر ویژه SL را مانند مثال ، و ارائه "راه حل های حالت عادی" تعریف می کند. برای W با وابستگی زمانی هارمونیک ،

$W _ {n mn}} (x، y، t) = A _ {n mn}} \ sin \ left ({\ frac \ m \ pi x {L_ {1}}} \ Right) \ sin \ left ( \ frac {n \ pi y {{L_ {2}} right \ Right) \ cos \ left (\ omega _ {{mn}} t \ Right)$

جایی که m و n عدد صحیح غیر صفر هستند ، A mn ثابتهای دلخواه هستند ، و

$\ omega _ {n mn}} ^ {2} = c ^ {2} \ left ({\ frac {m ^ {2} \ pi ^ {2}} {L_ {1} ^ {2}}} + { \ frac {n ^ {2} \ pi ^ {2}} {L_ {2} ^ {2}}} \ درست).$

توابع W mn مبنایی را برای فضای هیلبرت راه حل (تعمیم یافته) معادله موج ایجاد می کند. این است که، یک راه حل دلخواه W را می توان به یک جمع از این حالت، که در فرکانس های فردی خود ارتعاش تجزیه ω MN . این نمایندگی ممکن است به مبلغ بی نهایت همگرا نیاز داشته باشد .

معادله خطی مرتبه دوم [ ویرایش ]

برای مرتبه دوم خطی در یک بعد مکانی و مرتبه اول در زمان فرم:

$\ displaystyle f (x) \ frac {\ جزئی ^ {2} u} {\ جزئی x ^ {2}}} + g (x) \ frac {\ جزئی جزئی} {\ جزئی x}} + h (x) تو = {\ frac {\ جزئی تو u {\ جزئی t}} + k (t) تو ،$

${\ displaystyle u (a، t) = u (b، t) = 0، \ qquad u (x، 0) = s (x).}$

ما با جدا کردن متغیرها ، فرض می کنیم

${\ displaystyle u (x، t) = X (x) T (t).$

سپس معادله دیفرانسیل جزئی جزئی فوق ما ممکن است به شرح زیر باشد:

$\ frac {{\ hat L}} X (x) {X (x)}} = {\ frac {{\ hat hat M}} T (t)} {T (t)}$

جایی که

$\ displaystyle \ hat {L}} = f (x) \ frac {\ mathrm {d} ^ {2}} {\ mathrm {d} x ^ {2}}} + g (x) {\ frac \ mathrm {d}} {\ mathrm {d} x}} + h (x)، \ qquad {\ hat hat M}} = {\ frac {\ mathrm {d}} {\ mathrm {d} t} k + k (t).$

از آنجا که با تعریف ، L̂ و X ( x ) مستقل از زمان t و M̂ و T ( t ) از موقعیت x مستقل هستند ، بنابراین هر دو طرف معادله فوق باید برابر با یک ثابت باشند:

$\ displaystyle \ hat {L}} X (x) = \ lambda X (x)، \ qquad X (a) = X (b) = 0، \ qquad {\ hat {M}} T (t) = \ lambda T (t).$

اولین بار از این معادلات باید به عنوان یک مشکل استورم-لیوویل از نظر تابع ویژه حل شود X N ( X ) و مقادیر ویژه λ N . دومین این معادلات پس از مشخص شدن ارزشهای ویژه می توانند به صورت تحلیلی حل شوند.

$\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} t}} T_ {n} (t) = {\ bigl (} \ lambda _ {n} -k (t) {\ bigr) } T_ {n} (t)$

${\ displaystyle T_ {n} (t) = a_ {n} \ exp \ left (\ lambda _ {n} t- \ int _ {0} ^ {t} k (\ tau) \، \ mathrm {d \ tau \ درست)$

${\ displaystyle u (x، t) = \ sum _ {n} a_ {n} X_ {n} (x) \ exp \ left (\ lambda _ {n} t- \ int _ {0} ^ {t k (\ tau) \، \ mathrm {d} \ tau \ Right)$

$\ displaystyle a_ {n} = {\ frac {{\ bigl \ langle} X_ {n} (x)، s (x) \ bigr \ rangle}} {big bigl \ langle} X_ {n} (x ) ، X_ {n} (x) \ bigr \ rangle}}}}$

جایی که

$\ displaystyle \ bigl \ langle} y (x)، z (x) \ bigr \ rangle = \ int _ {a} ^ {b} y (x) z (x) w (x) \، \ mathrm {d} x،$

${\ displaystyle w (x) = {\ frac {\ exp \ left (\ int {\ frac {g (x)} {f (x)} \، \ mathrm {d} x \ Right)} {f ( ایکس)}}.}$

نمایندگی راه حل ها و محاسبه عددی [ ویرایش ]

معادله دیفرانسیل Sturm-Liouville ( 1 ) با شرایط مرزی ممکن است به روش تحلیلی حل شود ، که می تواند دقیق باشد یا یک تقریب را فراهم کند ، با استفاده از روش Rayleigh-Ritz یا با استفاده از روش ماتریس واریانس گرک و همکاران. [1] [2] [3]

از نظر عادی ، روشهای متنوعی نیز موجود است. در موارد دشوار ، ممکن است لازم باشد محاسبات میانی را تا چند صد رقم اعشار از دقت انجام دهید تا مقادیر ویژه ای را به درستی به چند مکان اعشاری بدست آورید.

روش های تیراندازی [4] [5] این روش را ادامه دهید با حدس زدن یک مقدار از λ ، حل مشکل مقدار اولیه تعریف شده توسط شرایط مرزی در یک نقطه پایانی، می گویند، ، فاصله [ ، ب ] ، مقایسه ارزش این راه حل طول می کشد در انتهای دیگر b با شرط مرزی مورد نظر دیگر ، و در آخر افزایش یا کاهش λ در صورت لزوم برای اصلاح مقدار اصلی. این استراتژی برای یافتن مقادیر ویژه مقدماتی کاربردی نیست. [ نیاز به توضیح ]
روش اختلاف محدود .
روش سری قدرت پارامتر طیفی (SPPS) [6] از تعمیم واقعیت زیر در مورد معادلات دیفرانسیل معمولی مرتبه دوم استفاده می کند: اگر y راه حل باشد که در هیچ نقطه ای از [ a ، b ] از بین نرود ، تابع

$y (x) \ int _ {a} ^ {x} {\ frac {{\ mathrm {d}} t} {p (t) y (t) ^ {2}}}$

راه حل همان معادله است و از نظر خطی مستقل از y است . علاوه بر این ، تمام راه حل ها ترکیبی خطی از این دو راه حل هستند. در الگوریتم SPPS ، باید با یک مقدار دلخواه λ شروع شود*
0(اغلب λ*
0= 0 ؛ لازم نیست یک مقادیر ویژه باشد) و هر راه حل y 0 از ( 1 ) با λ = λ*
0که در [ a ، b ] ناپدید نمی شود . (بحث در زیر راه های یافتن مناسب y 0 و λ*
0.) دو توالی از توابع X ( n ) ( t ) ، X̃ ( n ) ( t ) روی [ a ، b ] که به آن انتگرال های تکراری گفته می شوند ، به صورت بازگشتی به صورت زیر تعریف می شوند. ابتدا وقتی که n = 0 است ، آنها گرفته می شوند که به طور یکسان برابر 1 در [ a ، b ] هستند . برای به دست آوردن توابع بعدی آنها به صورت متناوب ضرب می شوند1/پی2
0و وای2
$\ displaystyle (5) \ qquad \ qquad X ^ {(n) (t) = {\ آغاز {موارد} \ displaystyle - \ int _ {a} ^ {x} X ^ {(n-1)} ( t) p (t) ^ {- 1} y_ {0} (t) ^ {- 2} \، \ mathrm {d} t & n {\ text {عجیب}} ، \\ [6pt] \ displaystyle \ quad \ int _ {a} ^ {x} X ^ {(n-1)} (t) y_ {0} (t) ^ {2} w (t) \، \ mathrm {d} t & n {\ متن {حتی} \ end {موارد}}}$

$\ displaystyle (6) \ qquad \ qquad {\ tilde {X}} ^ {(n) (t) = {\ آغاز {موارد} \ displaystyle \ quad \ int _ {a} ^ {x} {\ tilde {X}} ^ {(n-1)} (t) y_ {0} (t) ^ {2} w (t) \، \ mathrm {d} t & n {\ text {عجیب}} ، \\ [6pt ] \ displaystyle - \ int _ {a} ^ {x} {\ tilde {X}} ^ {(n-1) (t) p (t) ^ {- 1} y_ {0} (t) ^ -2} \، \ mathrm {d} t & n text \ text {حتی.}} \ end {موارد}}$

انتگرال های تکرار شده در حال حاضر به عنوان ضرایب در دو سری قدرت زیر در λ استفاده می شوند :

$\ displaystyle u_ {0} = y_ {0} \ sum _ {k = 0} ^ {\ infty} \ left (\ lambda - \ lambda _ {0} ^ {*} \ Right) ^ {k} {\ tilde {X}} ^ {(2k)}،$

$u_ {1} = y_ {0} \ sum _ {{k = 0}} ^ {\ infty} \ left (\ lambda - \ lambda _ {0} ^ {*} \ Right) ^ {k} X ^ {(2k + 1)}.$

سپس برای هر λ (واقعی یا پیچیده) ، u 0 و u 1 راه حل های مستقل خطی از معادله مربوطه ( 1 ) هستند . (توابع p ( x ) و q ( x ) از طریق تأثیرگذاری بر انتخاب y 0 در این ساخت و ساز شرکت می کنند .)

یکی دیگر ضرایب c 0 و c 1 را انتخاب می کند به طوری که ترکیب y = c 0 u 0 + c 1 u 1 اولین شرط مرزی را برآورده می کند ( 2 ) . این کار ساده است زیرا X ( n ) ( a ) = 0 و X̃ ( n ) ( a ) = 0 برای n > 0 انجام می شود . مقادیر X ( n ) ( b )و X̃ ( n ) ( b ) مقادیر u 0 ( b ) و u 1 ( b ) و مشتقات u ′ 0 ( b ) و u ′ 0 ( b ) را ارائه می دهد ، بنابراین شرط مرز دوم ( 3 ) تبدیل می شود. معادله در یک سری قدرت در λ . برای کارهای عددی ممکن است این سری به تعداد محدودی از اصطلاحات کوتاه شود و یک چند جمله ای قابل محاسبه در λ تولید شود که ریشه های تقریبی مقادیر خاص اوضاع به دنبال هستند.

هنگامی که λ = λ 0 ، این به ساخت اصلی که در بالا توضیح داده شده است برای یک راه حل بصورت خطی مستقل از یک داده خاص کاهش می یابد. بازنمودها (' 5 ' ) و (' 6 ' ) در تئوري اشتورم-ليول نيز کاربردهاي نظري دارند. [6]

ساخت یک راه حل غیرقابل استفاده [ ویرایش ]

روش SPPS می توانید، به خودی خود، مورد استفاده قرار گیرد برای پیدا کردن یک راه حل شروع Y 0 . معادله ( py ′) Consider = μqy را در نظر بگیرید ؛ یعنی ، q ، w و λ به ترتیب در ( 0 ) با 0 ، - q و μ جایگزین می شوند. سپس عملکرد ثابت 1 یک محلول غیرقابل انعطاف است که مربوط به مقادیر ویژه μ 0 = 0 است . در حالی که هیچ تضمینی وجود ندارد که تو 0 یا تو 1 نمی خواهد ناپدید می شوند، تابع پیچیده Y 0 = U0 + iu 1 هرگز از بین نمی رود زیرا دو راه حل مستقل از یک معادله SL معمولی نمی توانند همزمان به عنوان نتیجه قضیه جدایی Sturm از بین بروند . این ترفندبرای مقدار λ 0 = 0 راه حل y 0 از ( 1 ) را ارائه می دهد. در عمل اگر ( 1 ) ضرایب واقعی داشته باشد ، راه حل های مبتنی بر y 0 دارای بخش های تخیلی بسیار کوچکی هستند که باید دور ریخت.

منبع

https://en.wikipedia.org/wiki/Sturm%E2%80%93Liouville_theory

ادامه نظریه اشتورم-لیوویل

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 22:20

معادلات استورم-لیوویل به عنوان اپراتورهای دیفرانسیل خود متعهد [ ویرایش ]

نقشه برداری توسط:

${\ displaystyle Lu = - {\ frac {1} {w (x)}} سمت چپ ({\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ left [p (x) \، \ frac {\ mathrm {d} u} {\ mathrm {d} x}} \ Right] + q (x) u \ Right)$

می توان به عنوان یک عملگر خطی L نقشه برداری از یک تابع u به یک عملکرد دیگر Lu را مشاهده کرد ، و می توان آن را در زمینه تحلیل عملکردی مورد مطالعه قرار داد . در واقع می توان معادله ( 1 ) را به صورت زیر نوشت

${\ displaystyle Lu = \ lambda u.}$

این دقیقاً مسئله مقدماتی است؛ این است که، یکی به دنبال مقادیر ویژه لامبدا 1 ، λ 2 ، λ 3 ، ... و بردارهای ویژه متناظر تو 1 ، تو 2 ، تو 3 ، ... از L اپراتور. تنظیم مناسب این مشکل فضای هیلبرت است $\ displaystyle L ^ {2} ([a، b]، w (x) \، dx)$ با محصول مقیاس پذیر

$\ displaystyle \ langle f، g \ rangle = \ int _ {a} ^ {b} {\ overline {f (x)} g (x) w (x) \، \ mathrm {d} x.}$

در این فضا L بر روی توابع به اندازه کافی صاف تعریف شده است که شرایط مرزی عادی فوق را برآورده می کند. علاوه بر این ، L یک اپراتور خودمحور است:

$\ displaystyle \ langle Lf، g \ rangle = \ langle f، Lg \ rangle.}$

این امر می تواند بطور رسمی با استفاده از قطعات دوبار ادغام شود ، در حالی که شرایط مرزی به واسطه شرایط مرزی از بین می رود. پس از آن نتیجه می گیرد که مقادیر ویژه یک اپراتور Sturm-Liouville واقعی هستند و عملکردهای بنیادی L مربوط به مقادیر خاص ویژه متعامد متعامد هستند. با این حال ، این اپراتور بدون محدودیت است و از این رو وجود یک پایه متعارف ارتودنسی معمولی مشهود نیست. برای غلبه بر این مشکل ، باید به حلال نگاه کرد

$\ displaystyle \ سمت چپ (Lz \ راست) ^ {- 1} ، \ qquad z \ in \ mathbb {C} ،$

جایی که z به عنوان عدد واقعی انتخاب می شود که مقدمه ای خاص نیست. سپس ، محاسبه مقادیر حل شده برای حل معادله غیر همگن ، که می تواند با استفاده از فرمول تغییر پارامترها انجام شود . این نشان می دهد که حلال یک اپراتور انتگرال با هسته متقارن مداوم است (عملکرد سبز مسئله). به عنوان یک نتیجه از قضیه Arzelà-آسکولی ، این انتگرال جمع و جور و وجود یک توالی از مقادیر ویژه است α N که همگرا به 0 و تابع ویژه که به صورت به صورت orthonormal زیر از قضیه طیفی برای اپراتورهای جمع و جور . در آخر ، توجه داشته باشید که

$\ displaystyle \ left (Lz \ Right) ^ {- 1} u = \ alpha u، \ qquad Lu = \ left (z + \ alpha ^ {- 1} \ Right) u،$

معادل هستند ، بنابراین ممکن است بگیریم $\ displaystyle \ lambda = z + \ alfa ^ {- 1}$ با همان عملکردهای ویژه

اگر فاصله بی حد و مرز باشد ، یا اگر ضرایب در نقاط مرزی دارای مفرد باشند ، فرد L را مفرد می خواند . در این حالت ، طیف دیگر به تنهایی از مقادیر ویژه ای تشکیل نمی شود و می تواند یک جزء مداوم را شامل شود. هنوز یک گسترش عملکرد عملکردی مرتبط است (شبیه سری فوریه در مقابل تبدیل فوریه). این امر در مکانیک کوانتومی حائز اهمیت است ، زیرا معادله یک بعدی بعدی مستقل شرودینگر یک مورد خاص از معادله SL است.

کاربرد در مشکلات ارزش مرزی ناهمگن مرتبه دوم [ ویرایش ]

یک معادله دیفرانسیل خطی مرتبه دوم ناهمگن کلی را در نظر بگیرید

${\ displaystyle P (x) y '' + Q (x) y '+ R (x) y = f$

برای توابع داده شده ${\ نمایشگر P (x) ، Q (x) ، R (x) ، f (x)$ . مانند گذشته ، این می تواند به شکل SL کاهش یابد ${\ displaystyle Ly = f$ : نوشتن یک اپراتور SL به عنوان:

$\ displaystyle Lu = {\ frac {p} {w (x)}} u '' + {\ frac {p '} {w (x)} u' + {\ frac {q} {w (x) } تو ،}$

یکی سیستم را حل می کند:

$\ displaystyle p = Pw، \ quad p '= Qw، \ quad q = Rw.$

برای حل دو معادله اول کافی است ، که این مقدار به حل ( Pw ) Q = Qw یا

$\ displaystyle w '= {\ frac {Q-P'} {P}} w: = \ alpha w.$

راه حل این است:

${\ displaystyle w = \ exp \ left (\ int \ alpha \، \ mathrm {d} x \ right)، \ quad p = P \ exp \ left (\ int \ alpha \، \ mathrm {d} x \ Right ) ، \ quad q = R \ exp \ left (\ int \ alpha \، \ mathrm {d} x \ Right).$

با توجه به این تحول ، یکی برای حل کردن باقی مانده است:

${\ displaystyle Ly = f}$

به طور کلی ، اگر شرایط اولیه در برخی از نقاط مشخص شده باشد ، به عنوان مثال y ( a ) = 0 و y ′ ( a ) = 0 ، یک معادله دیفرانسیل مرتبه دوم با استفاده از روشهای معمولی قابل حل است و قضیه Picard-Lindelöf تضمین می کند که دیفرانسیل معادله در همسایگی نقطه ای که شرایط اولیه مشخص شده است ، یک راه حل منحصر به فرد دارد.

اما اگر به جای مشخص کردن مقادیر اولیه در یک نقطه واحد ، می خواهیم مقادیر را در دو نقطه مختلف (به اصطلاح مقادیر مرزی) ، به عنوان مثال y ( a ) = 0 و y ( b ) = 1 مشخص کنید ، مشکل به وجود می آید. خیلی سخت تر توجه كنید كه با افزودن یك تابع قابل تشخیص متفاوت مناسب به y ، كه مقادیر آن در a و b شرایط مرزی مورد نظر را برآورده می كند ، و با تزریق درون معادله دیفرانسیل پیشنهادی ، می توان بدون از دست دادن کلی فرض كرد كه شرایط مرزی از فرم y ( a ) = 0 وy ( b ) = 0 .

در اینجا، نظریه اشتورم-لیوویل می آید در بازی: در واقع، یک کلاس بزرگ از توابع F می تواند در شرایط از یک سری از eigenfunctions orthonormal گسترش U من از اپراتور لیوویل با مقادیر ویژه مربوط لامبدا من :

$\ displaystyle f (x) = \ sum _ {i} \ alpha _ {i} u_ {i} (x)، \ quad \ alpha _ {i} \ in {\ mathbb {R}}.}$

سپس یک راه حل برای معادله پیشنهادی بدیهی است:

$\ displaystyle y = \ sum _ {i} {\ frac {\ alpha _ {i}} {\ lambda _ {i}}} u_ {i}.$

این راه حل فقط در بازه a < x < b معتبر خواهد بود و ممکن است در مرزها شکست بخورد.

مثال: سری فوریه [ ویرایش ]

مشکل استورم-لیوویل را در نظر بگیرید:

$\ displaystyle (4) \ qquad \ qquad Lu = - {\ frac {\ mathrm {d} ^ {2} u} {\ mathrm {d} x ^ {2}}} = \ lambda u}$

زیرا ناشناخته ها λ و u ( x ) هستند . برای شرایط مرزی ، به عنوان مثال:

$u (0) = u (\ pi) = 0.$

مشاهده کنید که اگر k عدد صحیح باشد ، تابع

$\ displaystyle u_ {k} (x) = \ sin kx}$

یک راه حل با مقادیر ویژه λ = k 2 است . ما می دانیم که راه حل های یک مشکل SL پایه ای متعامد را تشکیل می دهد و از سری فوریه می دانیم که این مجموعه از عملکردهای سینوسی یک مبنای متعامد است. از آنجا که پایه های متعامد همیشه حداکثر هستند (با تعریف) نتیجه می گیریم که مشکل SL در این مورد مجرای بردار دیگری ندارد.

با توجه به موارد قبلی ، اجازه دهید اکنون مشکل ناهمگن را حل کنیم

${\ displaystyle Ly = x ، \ qquad x \ in (0 ، \ pi)$

با همان شرایط مرزی $\ displaystyle y (0) = y (\ pi) = 0$ . در این حالت ، ما باید f ( x ) = x را به عنوان یک سری فوریه گسترش دهیم. خواننده ممکن است را بررسی کنید، یا با یکپارچه سازی ∫ الکترونیکی ikx X د X و یا با مراجعه به جدول تبدیل فوریه، که ما در نتیجه بدست آوردن

$\ displaystyle Ly = \ sum _ {k = 1} ^ {\ infty} -2 {\ frac {\ left (-1 \ Right) ^ {k}} {k}} \ sin kx.$

این سری خاص فوریه به دلیل خواص همگرایی ضعیف ، مشکل ساز است. پیشینی مشخص نیست که آیا این سری به صورت نقطه همگرا است یا خیر. از آنجا که از تجزیه و تحلیل فوریه، از ضرایب فوریه هستند " مربع summable "، به همگرا سری فوریه در L 2 است که همه ما برای این نظریه خاص برای عملکرد. برای خواننده علاقه مند ذکر می کنیم که در این حالت ممکن است به نتیجه ای اعتماد کنیم که می گوید سری فوریه در هر نقطه از تفاوت پذیری همگرا می شود و در نقاط پرش (عملکرد x ، که به عنوان یک عملکرد دوره ای در نظر گرفته می شود ، دارای پرش در π ) همگرا می شود. به طور متوسط از حد چپ و راست (به همگرایی سری فوریه مراجعه کنید ).

بنابراین ، با استفاده از فرمول ( 4 ) ، راه حل را بدست می آوریم:

$\ displaystyle y = \ sum _ {k = 1} ^ {\ infty} 2 {\ frac {(-1) ^ {k}} {k ^ {3}}} \ sin kx = {\ tfrac {1 6}} (x ^ {3} - \ pi ^ {2} x).$

در این حالت ، ما می توانیم با استفاده از ضد تمایز پاسخ را پیدا کنیم ، اما این در بیشتر موارد زمانی که معادله دیفرانسیل در بسیاری از متغیرها باشد ، دیگر مفید نیست.

منبع

https://en.wikipedia.org/wiki/Sturm%E2%80%93Liouville_theory

نظریه اشتورم-لیوویل

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 22:13

در ریاضیات و کاربردهای آن ، تئوری کلاسیکاشتورم-لیوویل نظریه معادلات دیفرانسیل معمولی خطی مرتبه دوم واقعی از فرم است:

$\ displaystyle (1) \ qquad \ qquad {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \! \! \ left [\، p (x) {\ frac {\ mathrm {d } y} {\ mathrm {d} x}} \ Right] + q (x) y = - \ lambda \، w (x) y،$

برای توابع ضریب داده شده p ( x ) ، q ( x ) و w ( x )> 0 و یک تابع ناشناخته y از متغیر x رایگان . تابع w ( x ) ، که گاه با r ( x ) مشخص می شود ، عملکرد وزن یا تراکم نامیده می شود . همه معادلات دیفرانسیل معمولی خطی مرتبه دوم را می توان به این شکل کاهش داد.

در ساده ترین حالت که در آن تمام ضرایب مستمر در بازه محدود بسته [ ، ب ] و ص است مشتق مداوم، یک تابع Y نامیده می شود راه حل آن است که اگر به طور مداوم در مشتقپذیر ( ، ب ) و در معادله ( 1 ) در هر نقطه از ( ، ب ) . (در مورد کلیتر p ( x ) ، q ( x ) ، w ( x)) ، راه حل ها باید به معنای ضعیف درک شوند .) علاوه بر این ، y معمولاً برای برآورده کردن برخی شرایط مرزی در a و b لازم است . هر یک از این معادلات ( 1 ) همراه با شرایط مرزی آن ، یک مسئله اشتورم-لیوویل

مقدار λ در معادله مشخص نشده است: پیدا کردن λ که در آن یک راه حل غیرعادی وجود دارد بخشی از مشکل SL داده شده است. به این مقادیر λ ، در صورت وجود ، مقادیر اساسی مسئله گفته می شود ، و راه حل های مربوط عبارتند از عملکردهای اساسی مربوط به هر λ . این اصطلاحات به این دلیل است که راه حلها با مقادیر ویژه و عملکردهای ویژه یک اپراتور دیفرانسیل هرمیتیت در یک فضای مناسب با عملکرد مطابقت دارند.. نظریه اشتورم-لیوویل به بررسی وجود و رفتار بدون علامت ویژه مقادیر خاص ، نظریه کیفی مربوط به ویژگیهای ویژه و کامل بودن آنها در فضای عملکرد می پردازد.

این نظریه در ریاضیات کاربردی ، که در آن مشکلات SL بسیار معمول اتفاق می افتد ، به ویژه هنگام برخورد با معادلات دیفرانسیل جزئی خطی قابل تفکیک ، بسیار مهم است . به عنوان مثال ، در مکانیک کوانتومی ، معادله یک بعدی بعدی مستقل شرودینگر یک مسئله SL است.

گفته می شود که یک مسئله اشتورم-لیوویل معمولی است اگر p ( x ) ، w ( x )> 0 و p ( x ) ، p ′ ( x ) ، q ( x ) ، w ( x ) توابع مداوم بر روی متناهی باشند. فاصله [ a ، b ] ، و مشکل شرایط مرزی از فرم را از هم جدا کرده است :

$\ displaystyle (2) \ qquad \ qquad \ alpha _ {1} y (a) + \ alpha _ {2} y '(a) = 0 \ qquad \ qquad \ alpha _ {1} ^ {2} + \ آلفا _ {2} ^ {2}> 0 ،$

$\ displaystyle (3) \ qquad \ qquad \ beta _ {1} y (b) \، + \، \ beta _ {2} y '(b) = 0 \ qquad \ qquad \ beta _ {1} ^ { 2} + \ beta _ {2} ^ {2}> 0.$

نتیجه اصلی نظریه استورم-لیوویل بیان می کند که ، برای مسئله منظم استورم-لیوویل ( 1 ) ، ( 2 ) ، ( 3 ) :

مقادیر ویژه λ 1 ، λ 2 ، λ 3 ، ... واقعی هستند و می توانند به گونه ای شماره گذاری شوند

$\ lambda _ {1} <\ lambda _ {2} <\ lambda _ {3} <\ cdots <\ lambda _ {n} <\ cdots \ to \ infty؛$

مطابق با هر مقادیر خاص λ n یک عملکرد ویژه منحصر به فرد (تا چند برابر ثابت) y n ( x ) با دقیقا n -1 صفر در ( a ، b ) است که به عنوان راه حل اساسی th ( n ) نامیده می شود .
تابع ویژه نرمال تشکیل اساس orthonormal تحت W- کالا وزن درونی در فضای هیلبرت $\ displaystyle L ^ {2} ([a، b]، w (x) \، dx)$ . به این معنا که:

$\ displaystyle \ langle y_ {n، y_ {m} \ rangle = \ int _ {a} ^ {b} y_ {n} (x) y_ {m} (x) w (x) \، \ mathrm { d} x = \ delta _ {mn} ، \ \$ که در آن δ MN است دلتای کرونکر .

این نظریه پس از ژاک چارلز François Sturm (1803-1855) و جوزف لیوول (1809-1882) نامگذاری شده است .

فهرست

کاهش به فرم اشتورم-لیوویل [ ویرایش ]

گفته می شود که معادله دیفرانسیل ( 1 ) به شکل استورم-لیوویل یا فرم خود ترسیمی است . همه معادلات دیفرانسیل معمولی خطی مرتبه دوم را می توان در قالب سمت چپ ( 1 ) با ضرب هر دو طرف معادله با یک عامل یکپارچه سازی مناسب دوباره تغییر داد (گرچه در مورد معادلات دیفرانسیل جزئی مرتبه دوم نیز یکسان نیست. ، و یا اگر Y است بردار ). چند نمونه در زیر آمده است.

معادله بسل [ ویرایش ]

${\ displaystyle x ^ {2} y '' + xy '+ \ left (x ^ {2 - \ nu ^ {2} \ Right) y = 0$

که می تواند به شکل Sturm-Liouville نوشته شود (ابتدا با تقسیم بر x و سپس با فروپاشی دو اصطلاح در سمت چپ به یک ترم) به صورت زیر

${\ displaystyle \ left (xy '\ Right)$

معادله Legendre [ ویرایش ]

${\ displaystyle \ left (1-x ^ {2} \ Right) y '' - 2xy '+ \ nu (\ nu +1) y = 0$

از آنجا که می توان به راحتی در قالب اشتورم-لیوویل قرار داد د/د x(1 - x 2 ) = − 2 x ، بنابراین معادله Legendre معادل است

${\ displaystyle \ چپ (\ سمت چپ (1-x ^ {2} \ راست) y '\ Right)' + \ nu (\ nu +1) y = 0$

مثال با استفاده از یک عامل ادغام [ ویرایش ]

$\ displaystyle x ^ {3} y '' - xy '+ 2y = 0$

تقسیم بر همه در x 3 :

$y '' - {\ frac {1} {x ^ {2}}} y '+ {\ frac {2} {x ^ {3}} y = 0$

ضرب در یک عامل یکپارچه در

$\ displaystyle \ mu (x) = \ exp \ left (\ int - {\ frac {1} {x ^ {2}}} \، \ mathrm {d} x \ Right) = e ^ {\ frac {1 }{ایکس}}،}$

می دهد

$e ^ {{fr \ frac {1} {x}}}} y '' - {\ frac {e ^ {{fr \ frac {1} {x}}}}} x {^} '+ {\ frac {2e ^ {{{\ frac {1} {x}}}}} {x ^ {3}}} y = 0$

از آن زمان می توان به راحتی در قالب اشتورم-لیوویل قرار داد

$\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} e ^ {\ frac {1} {x}} = - - {\ frac {e ^ {\ frac {1} {x }} {x ^ {2}}}$

بنابراین معادله دیفرانسیل معادل است

$\ displaystyle \ left (e ^ {\ frac {1 {{x}} y '\ Right)' + {\ frac {2e ^ {\ frac {1} {x}}} {x ^ {3}}} y = 0.$

عامل یکپارچه سازی برای معادله مرتبه دوم [ ویرایش ]

$P (x) y '' + Q (x) y '+ R (x) y = 0$

ضرب در فاکتور یکپارچه سازی

$\ displaystyle \ mu (x) = {\ frac {1} {P (x)} \ exp \ left (\ int {\ frac {Q (x) {P (x)} \، \ mathrm { d} x \ درست) ،}$

و سپس جمع آوری شکل اشتورم-لیوویل را می دهد:

$\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} big \ bigl (} \ mu (x) P (x) y '{\ bigr)} + \ mu (x) R (x) y = 0 ،}$

یا به صراحت:

$left \ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ left (\ exp \ left (\ int {\ frac {Q (x) {P (x)}} \، \ mathrm {d} x \ Right) y '\ Right) + {\ frac {R (x)} {P (x)} \ exp \ left (\ int \ frac {Q (x)} {P ( x) =} \، \ mathrm {d} x \ درست) y = 0.$

منبع

https://en.wikipedia.org/wiki/Sturm%E2%80%93Liouville_theory

مثال بردار ویژه و مقدار ویژه ماتریس

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 20:38

بردار ویژه و مقدار ویژه ماتریس در متلب

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 20:36

2sqrt است. (3) ، آژانس ویژه 2sqrt (3) +3 و eigenveector 0 آخرین است.

مقادیر ویژه و مقادیر ویژه ماتریس Hadamard از نظم 4 که از یک ضرب تانسور ساخته شده اند چیست؟

توسط علی رضا نقش نیلچی | چهارشنبه بیست و پنجم تیر ۱۳۹۹ | 20:34

منبع

https://www.quora.com/What-are-the-eigenvalues-and-eigenvectors-of-the-Hadamard-matrix-of-order-4-constructed-from-a-tensor-product

ادامه ماتریس متقارن مشخص

توسط علی رضا نقش نیلچی | سه شنبه بیست و چهارم تیر ۱۳۹۹ | 20:56

فرم های درجه دوم [ ویرایش ]

مقاله اصلی: فرم درجه چهار قطعی

(کاملاً) شکل درجه دوم که مربوط به یک واقعیت است $n \ n n$ ماتریس $م$ این عملکرد است $\ displaystyle Q: \ mathbb {R} ^ {n} \ to \ mathbb {R}$ به طوری که $\ displaystyle Q (x) = x ^ {\ Texff {T}} Mx$ برای همه

$ایکس$ $م$ با تعویض آن می توان متقارن فرض کرد ${\ displaystyle {\ tfrac {1} {2}} \ left (M + M ^ {\ textf {T}} \ Right)$ .

یک ماتریس متقارن $م$ اگر مثبت باشد و فقط اگر فرم درجه دوم آن یک تابع محدب باشد ، مثبت است .

به طور کلی ، هر عملکرد درجه دوم از $\ mathbb {R} ^ {n$ به $\ mathbb {R$ می تواند به عنوان نوشته شود $\ displaystyle x ^ {\ textf {T}} Mx + x ^ {\ متنf T}} b + c$ جایی که $م$ متقارن است $n \ n n$ ماتریس ، $ب$ واقعی است $ن$ -وکتور ، و $ج$ یک ثابت واقعی این عملکرد درجه دوم کاملاً محدب است و از این رو حداقل و در صورت محدود بودن حداقل جهانی منحصر به فرد دارد $م$ قطعی مثبت است به همین دلیل ، ماتریس های مثبت مثبت نقش مهمی در مشکلات بهینه سازی بازی می کنند.

قطر همزمان مورب [ ویرایش ]

یک ماتریس متقارن و یک ماتریس قطعی متقارن و مثبت دیگر می تواند به طور همزمان مورب باشد ، اگرچه لزوماً از طریق یک تحول شباهت نیست . این نتیجه در مورد سه یا چند ماتریس گسترش نمی یابد. در این بخش برای پرونده واقعی می نویسیم. گسترش به مورد پیچیده فوری است.

اجازه دهید $م$ متقارن باشد و $ن$ یک ماتریس مشخص متقارن و مثبت. معادله ویژه مقدماتی عمومی را بنویسید $\ displaystyle (M- \ lambda N) x = 0$ جایی که ما آن را تحمیل می کنیم $ایکس$ عادی شود ، یعنی $\ displaystyle x ^ {\ textf T}} Nx = 1$ . اکنون ما برای تجزیه و تحلیل معکوس از تجزیه Cholesky استفاده می کنیم $ن$ مانند $\ displaystyle Q ^ {\ textf {T}} Q$ . ضرب توسط $س$ و اجازه دادن

$\ displaystyle x = Q ^ {\ textf T}} y}$ ، ما گرفتیم $\ displaystyle Q (M- \ lambda N) Q ^ {\ Texff {T}} y = 0$ ، که می تواند بازنویسی به عنوان ${\ نمایشگر \ چپ (QMQ ^ {\ Texff {T}} \ راست) y = \ lambda y$ جایی که $\ displaystyle y ^ {\ textf T}} y = 1$ . دستکاری اکنون بازده است $\ displaystyle MX = NX \ لامبدا$ جایی که $ایکس$ یک ماتریس است که به عنوان ستون های ویژه مجرای عمومی و $\ لامبدا$ یک ماتریس مورب از مقادیر ویژه ای تعمیم یافته است. در حال حاضر نسخه نهایی با $\ displaystyle X ^ {\ textf {T}}$ نتیجه نهایی را می دهد: $\ displaystyle X ^ {\ textf T}} MX = \ Lambda$ و $\ displaystyle X ^ {\ textf {T}} NX = I$ اما توجه داشته باشید که این دیگر یک مورب شدن متعامد با توجه به محصول داخلی است که در آن وجود ندارد $\ displaystyle y ^ {\ textf T}} y = 1$ . در حقیقت ، ما مورب هستیم $م$ با توجه به محصول داخلی ناشی از $ن$ .

توجه داشته باشید که این نتیجه با آنچه گفته می شود در مورد مورب همزمان در مقاله ماتریس Diagonalizable گفته می شود ، که اشاره به مورب همزمان با یک تغییر شباهت دارد ، مغایرت ندارد . نتیجه ما در اینجا بیشتر شبیه به مورب شدن همزمان دو شکل چهار درجه است و برای بهینه سازی یک فرم تحت شرایط از طرف دیگر مفید است. [3]

خواص [ ویرایش ]

سفارش جزئی ناشی از [ ویرایش ]

برای ماتریس مربع دلخواه $م$ ، $ن$ ما نوشتیم $\ displaystyle M \ geq N$ اگر $\ displaystyle MN \ geq 0$ یعنی $display \ displaystyle MN$ نیمه قطعی مثبت است این یک سفارش جزئی در مجموعه کلیه ماتریس های مربع را تعریف می کند . به طور مشابه می توان یک سفارش جزئی جزئی را تعریف کرد $\ displaystyle M> N$ . سفارش را سفارش Loewner می نامند .

معکوس از ماتریس قطعی مثبت [ ویرایش ]

هر ماتریس قطعی مثبت غیرقابل برگشت است و معکوس آن نیز قطعی مثبت است. [4] اگر $\ displaystyle M \ geq N> 0$ سپس

$\ displaystyle N ^ {- 1} \ geq M ^ {- 1> 0$ . [5] علاوه بر این ، با قضیه حداقل حداکثر ، k بزرگترین ارزش ویژه ای $م$ بزرگتر از k بزرگترین مقدمه ویژه ای است $ن$ .

مقیاس گذاری [ ویرایش ]

اگر $م$ قطعی مثبت است و $r> 0$ یک عدد واقعی است ، پس ${\ displaystyle rM$ قطعی مثبت است [6]

افزودنی [ ویرایش ]

اگر $م$ و $ن$ مثبت مثبت هستند ، پس جمع $م + ن$ همچنین قطعی مثبت است. [6]

ضرب [ ویرایش ]

اگر $م$ و $ن$ مثبت هستند ، پس از آن محصولات $MNM$ و $NMN$ همچنین قطعی مثبت هستند. اگر $\ displaystyle MN = NM$ ، سپس $MN$ همچنین قطعی مثبت است.
اگر $م$ پس از آن semidefinite مثبت است $\ displaystyle Q ^ {\ textf T}} MQ$ semidefinite مثبت است. اگر $م$ قطعی مثبت است و $س$ دارای رتبه ستون کامل ، پس از آن $\ displaystyle Q ^ {\ textf T}} MQ$ قطعی مثبت است [7]

تجزیه Cholesky [ ویرایش ]

برای هر ماتریس $آ$ ، ماتریکس $A ^ {*} A$ semidefinite مثبت است ، و ${\ displaystyle \ operatorname {rank} (A) = \ operatorname {rank} (A ^ {*} A)$ . برعکس ، هر ماتریس نیمه قطعی مثبت هرمیتی $م$ می تواند به عنوان نوشته شود $\ displaystyle M = LL ^ {*}}$ ، جایی که $ل$ مثلث پایین است. این تجزیه Cholesky است . اگر $م$ قطعی مثبت نیست ، سپس برخی از عناصر مورب $ل$ ممکن است صفر باشد

یک ماتریس هرمیتی $م$ مثبت است اگر و فقط اگر تجزیه منحصر به فرد Cholesky ، یعنی ماتریس $م$ اگر تنها یک ماتریس مثلثی پایین منحصر به فرد وجود داشته باشد ، مثبت است $ل$ ، با عناصر مورب واقعی و کاملاً مثبت ، به گونه ای که $\ displaystyle M = LL ^ {*}}$ .

ریشه مربع [ ویرایش ]

یک ماتریس $م$ نیمه قطعی مثبت است اگر و فقط اگر ماتریس نیمه قطعی مثبت وجود دارد $ب$ با $\ displaystyle B ^ {2} = M$ . این ماتریس $ب$ منحصر به فرد است، [8] نامیده می شود ریشه مربع از $م$ ، و با آن علامت گذاری شده است $\ displaystyle B = M ^ {\ frac {1} {2}}$ (ریشه مربع $ب$ این نیست که با ماتریس اشتباه گرفته شود $ل$ در عامل سازی Cholesky $\ displaystyle M = LL ^ {*}}$ ، که گاهی اوقات ریشه مربع نیز نامیده می شود $م$ )

اگر $\ displaystyle M> N> 0$ سپس $\ displaystyle M ^ {\ frac {1} {2}}> N ^ {\ frac {1} {2}}> 0$ .

فرعی [ ویرایش ]

هر زیرمجاز اصلی یک ماتریس مثبت مثبت قطعی مثبت است.

ردیابی [ ویرایش ]

مدخل های مورب ${\ displaystyle m_ {ii}}$ یک ماتریس قطعی مثبت واقعی و غیر منفی است. در نتیجه اثری ، $\ displaystyle \ operatorname {tr} (M) \ geq 0$ . علاوه بر این ، [9] از آنجا که هر زیر ماتریس اصلی (به طور خاص ، 2 - 2) قطعی مثبت است ،

$\ displaystyle \ left | m_ {ij} \ Right | \ leq {\ sqrt {m_ {ii} m_ {jj}}} \ leq {\ frac {m_ {ii} + m_ {jj}} {2}} \ چهارم \ من همه ، j}$

و بنابراین

$\ displaystyle \ max_ {i، j} \ left | m_ {ij} \ right | \ leq \ max _ {i} \ left | m_ {ii} \ Right |$

یک $n \ n n$ ماتریس هرمیتی $م$ در صورت برابری نابرابری های زیر ، قطعی مثبت است: [10]

$\ displaystyle \ operatorname {tr} (M)> 0 \ quad \ mathrm {و} \ quad {\ frac {(\ operatorname {tr} (M)) ^ {2}} {\ operatorname {tr} (M ^ {2})}}> n-1.$

محصول Hadamard [ ویرایش ]

اگر $\ displaystyle M ، N \ geq 0$ ، با اينكه $MN$ لازم نیست نیمه نهایی مثبت ، محصول Hadamard باشد $\ displaystyle M \ Circ N \ geq 0$ (این نتیجه اغلب قضیه محصول Schur نامیده می شود ). [11]

با توجه به محصول Hadamard از دو ماتریس semidefinite مثبت $\ displaystyle M = (m_ {ij}) \ geq 0$ ، $N \ geq 0$ ، دو نابرابری قابل توجه وجود دارد:

نابرابری اوپنهایم: $\ displaystyle \ det (M \ Circ N) \ geq \ det (N) \ prod \ nolimits _ {i} m_ {ii}.}$ [12]
$\ displaystyle \ det (M \ Circ N) \ geq \ det (M) \ det (N)$ . [13]

محصول کرونکر [ ویرایش ]

اگر $\ displaystyle M ، N \ geq 0$ ، با اينكه $MN$ لازم نیست semidefinite مثبت ، محصول Kronecker باشد $\ displaystyle M \ otimes N \ geq 0$ .

محصول فروبنیوس [ ویرایش ]

اگر $\ displaystyle M ، N \ geq 0$ ، با اينكه $MN$ لازم نیست semidefinite مثبت ، محصول Frobenius باشد $\ displaystyle M: N \ geq 0$ (لنکستر - تیزمنتسکی ، تئوری ماتریس ، ص 218).

محدب [ ویرایش ]

مجموعه ماتریسهای متقارن نیمه مثبت مثبت محدب است . یعنی اگر $م$ و $ن$ semidefinite مثبت هستند ، پس برای هر $\ آلفا$ بین 0 و 1 ، $\ displaystyle \ alpha M + (1- \ alpha) N$ همچنین semidefinite مثبت است. برای هر وکتور $ایکس$ :

$\ displaystyle x ^ {\ textf {T}} \ left (\ alpha M + (1- \ alpha) N \ Right) x = \ alpha x ^ {\ textf T}} Mx + (1- \ alpha) x ^ \ textf T}} Nx \ geq 0.$

این ویژگی تضمین می کند که مشکلات برنامه نویسی نیمه نهایی به یک راه حل بهینه در سطح جهانی تبدیل می شوند.

منبع

https://en.wikipedia.org/wiki/Definite_symmetric_matrix

ادامه ماتریس متقارن مشخص

توسط علی رضا نقش نیلچی | سه شنبه بیست و چهارم تیر ۱۳۹۹ | 20:56

رابطه با کسین [ ویرایش ]

قطعیت مثبت یک ماتریس ${\ نمایشگر A}$ بیان می کند که زاویه $\ تتا$ بین هر بردار $ایکس$ و تصویر آن $تبر$ همیشه ... هست 2} $\ displaystyle - \ pi / 2 <\ theta <+ \ pi / 2}$ :

$\ displaystyle \ cos \ theta = {\ frac {x ^ {T} Ax} {\ left \ Vert x \ Right \ Vert \ left \ Vert Axe \ right \ Vert}} = {\ frac {\ langle x، Ax \ rangle} {\ چپ \ Vert x \ right \ Vert \ left \ Vert Ax \ Right \ Vert}}، \ theta = \ta (x، Ax) = {\ widehat {x، Ax}} = {\ text زاویه بین}} x {\ متن و}} تبر$

خصوصیات بیشتر [ ویرایش ]

اگر $م$ یک ماتریس Toeplitz متقارن ، یعنی ورودی ها است $m_ {ij$ به عنوان تابعی از اختلاف شاخص مطلق آنها آورده شده است: $\ displaystyle m_ {ij} = ساعت (| ij |)}$ و نابرابری شدید
$\ displaystyle \ sum \ nolimits _ {j \ neq 0} \ left | h (j) \ Right | <h (0)$
پس از آن $م$ است به شدت مثبت مشخص شده است.
اجازه دهید $M> 0$ و $ن$ هرمیتی اگر $\ displaystyle MN + NM \ geq 0$ (احترام ، $\ displaystyle MN + NM> 0$ ) سپس $\ displaystyle N \ geq 0$ ( $N> 0$ ) [14]
اگر $M> 0$ واقعی است ، پس وجود دارد $\ delta> 0$ به طوری که $\ displaystyle M> \ delta I$ ، جایی که $من$ است ماتریس .
اگر $M_k$ نشان دهنده پیشرو است $k \ بار k$ جزئی، ${\ displaystyle \ det \ left (M_ {k} \ Right) / \ det \ left (M_ {k-1} \ Right)$ است ک هفتم محور در طول تجزیه LU .
یک ماتریس منفی قطعی است اگر آن K- سفارش هفتم منجر جزئی اصلی منفی زمانی است $ک$ عجیب است و مثبت $ک$ یکنواخت است
یک ماتریس $م$ اگر فقط بعنوان ماتریس گرمی برخی از بردارها ایجاد شود ، نیمه کاره مثبت است . بر خلاف مورد قطعی مثبت ، این بردارها نیازی به مستقل بودن خطی ندارند.

ماتریس هرمیتی در صورتی که تنها همه خردسالان اصلی آن غیرقانونی باشند semidefinite مثبت است. با این وجود ، توجه به افراد خردسال اصلی اصلی کافی نیست ، همانطور که در ماتریس مورب با مدخل 0 و 1-checked بررسی می شود.

بلوک ماتریس [ ویرایش ]

آ مثبت ${\ نمایشگر 2n \ بار 2n$ ماتریس ممکن است توسط بلوک ها نیز تعریف شود :

$\ displaystyle M = {\ آغاز {bmatrix} A&B \\ C&D \ end {bmatrix}}$

که در آن هر بلوک است $n \ n n$ . با استفاده از وضعیت مثبت ، بلافاصله از آن پیروی می کند $آ$ و $د$ هرمیتی هستند ، و $\ displaystyle C = B ^ {*}}$ .

ما آن را داریم $\ displaystyle z ^ {*} Mz \ geq 0$ برای همه پیچیده $z$ ، و به ویژه برای $\ displaystyle z = [v، 0] ^ {\ textf T}}$ . سپس

$\ displaystyle {\ fill {bmatrix} v ^ {*} & 0 \ end {bmatrix}} {\ fill bmatrix} A&B \\ B ^ {*} & D \ end {bmatrix} {\ fill bmatrix} v \ \ 0 \ end {bmatrix}} = v ^ {*} Av \ geq 0.$

یک استدلال مشابه می تواند در مورد آن اعمال شود $د$ و بنابراین نتیجه می گیریم که هر دو $آ$ و $د$ همچنین باید ماتریس های مشخص مثبت باشند.

نتایج مکالمه را می توان با شرایط قوی تر روی بلوک ها اثبات کرد ، برای مثال با استفاده از مکمل Schur .

فوق العاده محلی [ ویرایش ]

یک فرم کلی درجه دوم $f (\ mathbf {x})$ بر $ن$ متغیرهای واقعی $x_ {1} ، \ ldots ، x_ {n$ همیشه می تواند به صورت نوشته شود $\ displaystyle \ mathbf {x} ^ {\ textf {T}} M \ mathbf {x}$ جایی که $\ mathbf {x$ وکتور ستون با آن متغیرها ، و $م$ یک ماتریس واقعی متقارن است. بنابراین ، مثبت بودن ماتریس بدین معنی است $f$ حداقل یک (صفر) منحصر به فرد دارد $\ mathbf {x$ صفر است و برای سایرین کاملاً مثبت است $\ mathbf {x$ .

به طور کلی ، یک عملکرد واقعی دو برابر متفاوت است $f$ بر $ن$ متغیرهای واقعی دارای حداقل محلی در آرگومان ها هستند $x_ {1} ، \ ldots ، x_ {n$ اگر شیب آن صفر باشد و Hessian آن (ماتریس همه مشتقات دوم) در آن نقطه نیمه قطعی مثبت است. برای ماتریس های قطعی و نیمه قطعی منفی می توان اظهارات مشابهی ارائه کرد.

کواریانس [ ویرایش ]

در آمار ، ماتریس کواریانس از توزیع احتمال چند متغیره همیشه مثبت و نیمه قطعی است. و مثبت قطعی است مگر اینکه یک متغیر عملکرد خطی دقیق دیگران باشد. برعکس ، هر ماتریس نیمه قطعی مثبت ماتریس کواریانس برخی توزیع چند متغیره است.

برنامه افزودنی برای ماتریس های مربع غیر هرمی [ ویرایش ]

تعریف قطعی مثبت را می توان با تعیین هر ماتریس پیچیده تعمیم داد $م$ (به عنوان مثال غیر متقارن واقعی) به عنوان قطعی مثبت اگر $\ displaystyle \ Re \ left (z ^ {*} Mz \ Right)> 0$ برای همه بردارهای پیچیده غیر صفر $z$ ، جایی که ${\ displaystyle \ Re (c)$ قسمت واقعی یک شماره پیچیده را نشان می دهد $ج$ . [15] فقط قسمت هرمیتی ${\ displaystyle {\ tfrac {1} {2}} \ left (M + M ^ {*} \ Right)$ تعیین می کند که آیا ماتریس مثبت قطعی است یا به معنای باریک بالا در بالا ارزیابی می شود. به همین ترتیب ، اگر $ایکس$ و $م$ ما واقعی هستیم $\ displaystyle x ^ {\ textf {T}} Mx> 0$ برای همه بردارهای غیرزرو واقعی $ایکس$ اگر و فقط اگر قسمت متقارن باشد ${\ displaystyle {\ tfrac {1} {2}} \ left (M + M ^ {\ textf {T}} \ Right)$ از نظر باریک قطعی مثبت است. بلافاصله مشخص است که $\ displaystyle x ^ {\ textf {T}} Mx = x_ {i} M_ {ij} x_ {j}$ نسبت به جابجایی M بی حساس است.

در نتیجه ، یک ماتریس واقعی غیر متقارن تنها با مقادیر ویژه مقادیر مثبت نیازی به قطعیت مثبت ندارد. به عنوان مثال ، ماتریس $\ displaystyle M = \ سمت چپ [{\ شروع {smallmatrix} 4 & 9 \\ 1 & 4 \ end smallmatrix} \ Right]$ دارای مقادیر ویژه ای مثبت هنوز قطعی مثبت نیست. به ویژه ارزش منفی از $\ displaystyle x ^ {\ textf {T}} Mx$ با انتخاب به دست می آید $\ displaystyle x = \ سمت چپ [{\ شروع {smallmatrix} -1 \\ 1 \ end {smallmatrix}} \ Right]$ (که eigenveector همراه با مقادیر ویژه منفی قسمت متقارن از است $م$ )

به طور خلاصه ، وجه تمایز قضیه واقعی و پیچیده این است که ، یک اپراتور مثبت محدود در فضای پیچیده هیلبرت لزوماً هرمیتی یا خود متعهد است. ادعای عمومی را می توان با استفاده از هویت قطبی شدن استدلال کرد . این در واقعیت دیگر صادق نیست.

برنامه ها [ ویرایش ]

ماتریس رسانایی گرما [ ویرایش ]

قانون انتقال حرارت فوریه ، شار گرما را ارائه می دهد $ق$ از نظر شیب دما $\ displaystyle g = \ nabla T$ برای رسانه های ناهمسانگرد به عنوان نوشته شده است $\ displaystyle q = -Kg$ ، که در آن

$ک$ ماتریس هدایت حرارتی متقارن است. منفی در قانون فوریه درج شده است تا منعکس کننده این انتظار باشد که گرما همیشه از گرما به سرما جاری می شود. به عبارت دیگر ، از آنجا که شیب دما $گرم$ همیشه از سرما به گرما ، شار گرما اشاره دارد $ق$ انتظار می رود که محصول داخلی منفی داشته باشد $گرم$ به طوری که $\ displaystyle q ^ {\ textf {T}} g <0$ . جایگزینی قانون فوریه سپس این انتظار را به وجود می آورد $\ displaystyle g ^ {\ textf {T}} کیلوگرم> 0$ دلالت بر اینکه ماتریس رسانایی باید قطعی مثبت باشد.

ادامه ماتریس متقارن مشخص

توسط علی رضا نقش نیلچی | سه شنبه بیست و چهارم تیر ۱۳۹۹ | 20:55

مقدمات ویژه [ ویرایش ]

اجازه دهید $م$ , $n \ n n$ ماتریس هرمیتی .

$م$ مثبت و قطعی است اگر و فقط اگر همه ارزشهای ویژه آن مثبت باشد.
$م$ نیمه قطعی مثبت است اگر و فقط اگر تمام مقادیر ویژه آن غیر منفی باشد.
$م$ اگر منفی باشد و فقط اگر تمام مقادیر ویژه آن منفی باشد ، قطعی منفی است
$م$ منفی نیمه قطعی است اگر و فقط اگر همه مقادیر ویژه آن مثبت نیستند.
$م$ نامشخص است اگر و فقط اگر هم مقادیر خاص و منفی مثبت داشته باشد.

اجازه دهید $\ displaystyle P ^ {- 1} DP$ باشد تجارتی ویژه $م$ ، جایی که $پ$ یک ماتریس پیچیده واحد که ردیف هایی تشکیل گردیده اساس orthonormal از بردارهای ویژه از

$م$ و $د$ یک ماتریس مورب واقعی است که مورب اصلی آن حاوی مقادیر ویژه ای است . ماتریکس $م$ ممکن است به عنوان یک ماتریس مورب در نظر گرفته شود

$د$ که در مختصات پایه دوباره بیان شده است $پ$ . به طور خاص ، تغییر یک به یک متغیر ${\ displaystyle y = Pz$ نشان میدهد که $\ displaystyle z ^ {*} Mz}$ برای هر بردار پیچیده واقعی و مثبت است $z$ اگر و تنها اگر $\ displaystyle y ^ {*} Dy}$ برای هر کسی واقعی و مثبت است $ی$ ؛ به عبارت دیگر ، اگر $د$ قطعی مثبت است در مورد ماتریس مورب ، این درست است اگر هر عنصر مورب اصلی - یعنی هر مقادیر ویژه ای از $م$ مثبت است. از آنجا که قضیه طیفی همه مقادیر مهم یک ماتریس هرمیتی را واقعی می داند ، می تواند مثبت بودن مقادیر ویژه را با استفاده از قاعده دکارت در مورد علائم متناوب ، هنگامی که چند جمله ای مشخصه یک ماتریس واقعی ، متقارن بررسی کرد. $م$ موجود است.

خصوصیات [ ویرایش ]

اجازه دهید $م$ $n \ n n$ ماتریس هرمیتی . خواص زیر معادل می باشد $م$ مثبت بودن قطعی:

فرم کنجد مربوط به یک محصول داخلی است

فرم sesquilinear تعریف شده توسط $م$ این عملکرد است $\ displaystyle \ langle \ cdot، \ cdot \ rangle$ از جانب $\ displaystyle \ mathbb {C} ^ {n} \ بار \ mathbb {C} ^ {n}$ به $\ mathbb {C} ^ {n$ به طوری که $\ displaystyle \ langle x، y \ rangle: = y ^ {*} Mx$ برای همه $ایکس$ و $ی$ که در $\ mathbb {C} ^ {n$ ، جایی که $y ^ {*$ پیوند مزدوج است $ی$ . برای هر ماتریس پیچیده $م$ ، این فرم به صورت خطی است $ایکس$ و نیمه تمام در $ی$ . بنابراین، فرم است محصول داخلی در $\ mathbb {C} ^ {n$ اگر و تنها اگر $\ displaystyle \ langle z، z \ rangle$ برای همه غیروزارها واقعی و مثبت است $z$ ؛ این در صورتی است که فقط و فقط اگر $م$ قطعی مثبت است (در واقع ، هر محصول درونی در $\ mathbb {C} ^ {n$ در این مد از یک ماتریس مشخص مثبت هرمیتی ناشی می شود.)

این ماتریس گرم مجموعه ای از بردارهای مستقل خطی است

اجازه دهید $x_ {1} ، \ ldots ، x_ {n$ لیستی از $ن$ بردارهای خطی مستقل از برخی از فضای بردار پیچیده با یک محصول داخلی $\ langle \ cdot ، \ cdot \ rangle$ . می توان تأیید کرد که ماتریس گرام $م$ از آن بردارها تعریف شده توسط $\ displaystyle M_ {ij} = \ langle x_ {i}، x_ {j} \ rangle$ ، همیشه مثبت قطعی است. برعکس ، اگر $م$ قطعاً مثبت است ، یک ترکیب تجسمی دارد $\ displaystyle P ^ {- 1} DP$ جایی که $پ$ واحد است ، $د$ مورب و همه عناصر مورب $\ displaystyle D_ {ii} = \ lambda _ {i}}$ از {\ نمایشگر D} $د$ واقعی و مثبت هستند اجازه دهید $ه$ ماتریس مورب واقعی با ورودی باشد $\ displaystyle E_ {ii} = {\ sqrt {\ lambda _ {i}}}}$ بنابراین $\ displaystyle E ^ {2} = D$ ؛ سپس $\ displaystyle P ^ {- 1} DP = P ^ {*} DP = P ^ {*} EEP = (EP) ^ {*} EP}$ . حالا اجازه می دهیم $x_ {1} ، \ ldots ، x_ {n$ ستون باشد $EP$ . این بردارها بطور خطی مستقل هستند و طبق موارد فوق $م$ ماتریس گرام آنها ، تحت محصول استاندارد داخلی است $\ mathbb {C} ^ {n$ ، برای مثال $\ displaystyle \ langle x_ {i}، x_ {j} \ rangle = x_ {i} ^ {\ ast} x_ {j}$ .

خردسالان اصلی آن همه مثبت هستند

K هفتم منجر جزئی اصلی از یک ماتریس $م$ است تعیین از آن بالا سمت چپ $k \ بار k$ ماتریس فرعی به نظر می رسد که اگر همه این عوامل تعیین کننده مثبت باشند ، یک ماتریس مثبت است. این شرط به عنوان معیار سیلوستر شناخته می شود و یک آزمایش کارآمد از قطعیت مثبت یک ماتریس واقعی متقارن را فراهم می کند. یعنی ، با استفاده از عملیات ردیف ابتدایی ، ماتریس به یک ماتریس مثلثی فوقانی کاهش می یابد ، همانطور که در قسمت اول روش حذف گاوسی ، با مراقبت از حفظ نشانه تعیین کننده آن در طی فرآیند چرخش . از آنجا که ک هفتم منجر جزئی اصلی یک ماتریس مثلثی کالا از عناصر مورب تا آن را به ردیف است $ک$ معیار سیلوستر معادل بررسی این است که آیا عناصر مورب آن همه مثبت است یا خیر. این وضعیت را می توان هر بار که یک ردیف جدید بررسی کرد $ک$ از ماتریس مثلثی بدست می آید.

منبع

https://en.wikipedia.org/wiki/Definite_symmetric_matrix

ماتریس متقارن مشخص

توسط علی رضا نقش نیلچی | سه شنبه بیست و چهارم تیر ۱۳۹۹ | 20:54

سازگاری بین تعاریف واقعی و پیچیده [ ویرایش ]

از آنجا که هر ماتریس واقعی نیز یک ماتریس پیچیده است ، تعاریف "قطعیت" برای این دو کلاس باید موافق باشند.

برای ماتریس های پیچیده ، متداول ترین تعریف می گوید: $م$ مثبت و مشخص است اگر و فقط اگر $\ displaystyle z ^ {*} Mz}$ برای همه بردارهای ستونی پیچیده غیر صفر واقعی و مثبت است $z$ این شرایط دلالت بر این امر دارد $م$ هرمیتی است (یعنی انتقال آن برابر است با ترکیب آن). برای دیدن این موضوع ، ماتریس ها را در نظر بگیرید ${\ displaystyle A = {\ tfrac {1} {2}} \ left (M + M ^ {*} \ Right))$ و $left \ displaystyle B = {\ tfrac {1} {2i}} \ سمت چپ (MM ^ {*} \ سمت راست)}$ ، به طوری که $\ displaystyle M = A + iB$ و $\ displaystyle z ^ {*} Mz = z ^ {*} Az + iz ^ {*} Bz$ . ماتریس

$آ$ و $ب$ بنابراین هرمیتی هستند $\ displaystyle z ^ {*} آز}$ و $\ displaystyle z ^ {*} Bz}$ بطور جداگانه واقعی هستند اگر $\ displaystyle z ^ {*} Mz}$ پس واقعی است $\ displaystyle z ^ {*} Bz}$ باید برای همه صفر باشد $z$ . سپس $ب$ ماتریس صفر است و ${\ displaystyle M = A$ ثابت کرد که $م$ هرمیتی است.

با این تعریف ، یک ماتریس واقعی مثبت مشخص است $م$ هرمیتی ، از این رو متقارن است. و $\ displaystyle z ^ {\ textf {T}} Mz}$ برای همه بردارهای ستون واقعی غیر صفر مثبت است $z$ . با این حال شرط آخر تنها برای این کافی نیست $م$ مثبت و قطعی باشد به عنوان مثال ، اگر

$M = begin \ fill bmatrix} 1 & 1 \\ - 1 & 1 \ end {bmatrix}}،$

سپس برای هر بردار واقعی $z$ با مدخل ها $آ$ و $ب$ ما داریم $\ displaystyle z ^ {\ textf {T}} Mz = (a + b) a + (- a + b) b = a ^ {2} + b ^ {2}}$ ، که همیشه مثبت است اگر $z$ صفر نیست اما اگر $z$ وکتور پیچیده ای است که دارای مدخل است $1$ و $من$ ، یکی می شود

$\ displaystyle z ^ {*} Mz = [1، -i] M [1، i] ^ {\ Texff {T}} = [1 + i، 1-i] [1، i] ^ {\ متنf T}} = 2 + 2i$

که واقعی نیست از این رو، $م$ قطعی مثبت نیست.

از طرف دیگر ، برای یک ماتریس واقعی متقارن $م$ ، شرایط

$\ displaystyle z ^ {\ textf {T}} Mz> 0$ برای همه بردارهای غیرزرو واقعی $z$ " به این معنی است $م$ مثبت به معنای پیچیده است.

نشانه گذاری [ ویرایش ]

اگر یک ماتریس هرمیتی $م$ مثبت است نیمه قطعی ، گاهی می نویسد $M \ succeq 0$ و اگر $م$ مثبت قطعی است که می نویسد $\ displaystyle M \ succ 0$ . برای بیان آن $م$ نیمه قطعی منفی است که می نویسد $\ displaystyle M \ preceq 0$ و به بیان آن $م$ قطعی منفی است که می نویسد $\ displaystyle M \ prec 0$ .

این مفهوم از تجزیه و تحلیل عملکردی ناشی می شود که در آن ماتریس های نیمه مثبت مثبت عملگرهای مثبت را تعریف می کنند .

یک نماد جایگزین رایج است $\ displaystyle M \ geq 0$ $\ displaystyle M> 0$ $\ displaystyle M \ leq 0$ و $display \ نمایشگر M <0$ به ترتیب برای ماتریسهای نیمه قطعی مثبت و مثبت-مثبت ، منفی نیمه قطعی و منفی-قطعی. این ممکن است گیج کننده باشد ، زیرا بعضی اوقات ماتریس های غیر منفی (به ترتیب ، ماتریس های غیرمخرب) نیز از این طریق مشخص می شوند.

مثالها [ ویرایش ]

ماتریس $\ displaystyle I = {\ fill bmatrix 1 & 0 \\ 0 & 1 \ end {bmatrix}}$ قطعی مثبت است (و به همین ترتیب نیمه مثبت قطعی نیز مثبت است). این یک ماتریس متقارن واقعی است ، و برای هر بردار ستونی غیر صفر z با ورودی های واقعی a و b ،
$\ displaystyle z ^ {\ Texff {T}} Iz = {\ آغاز {bmatrix} a & b \ end {bmatrix}} {\ fill bmatrix 1 & 0 \\ 0 & 1 \ end {bmatrix}} {\ fill {bmatrix} a \\ b \ end {bmatrix}} = a ^ {2} + b ^ {2}$ .
به عنوان یک ماتریس پیچیده ، برای هر بردار ستونی غیر صفر z که دارای ورودی های پیچیده a و b است ، مشاهده می شود
$\ displaystyle z ^ {*} Iz = {\ fill {bmatrix} {\ overline {a}} & {\ overline {b}} \ end {bmatrix}} {\ fill bmatrix 1 & 0 \\ 0 & 1 \ end { bmatrix}} {\ fill {bmatrix a \\ b \ end {bmatrix}} = {\ overline {a}} a + {\ overline {b}} b = | a | ^ {2} + | b | ^ 2$ .
در هر صورت ، از آن زمان نتیجه مثبت است $z$ وکتور صفر نیست (یعنی حداقل یکی از آنها $آ$ و $ب$ صفر نیست)
ماتریس متقارن واقعی
$\ displaystyle M = {\ fill bmatrix 2 & -1 & 0 \\ - 1 & 2 & -1 \\ 0 & -1 & 2 \ end bmatrix}}}$
مثبت است- از آنجا که برای هر بردار ستون غیر صفر z با مدخلهای a ، b و c ، داریم
${\ displaystyle {\ شروع {تراز شده} z ^ {\ Texsf {T}} Mz = \ سمت چپ (z ^ {\ Texff {T}} M \ سمت راست) z & = {\ fill bmatrix} (2a-b) & (-a + 2b-c) & (- b + 2c) \ end {bmatrix}} {\ fill bmatrix} a \\ b \\ c \ end {bmatrix} \\ & = (2a-b) a + (-a + 2b-c) b + (- b + 2c) c \\ & = 2a ^ {2} -ba-ab + 2b ^ {2} -cb-bc + 2c ^ {2} \\ & = 2a ^ {2} -2ab + 2b ^ {2} -2bc + 2c ^ {2} \\ & = a ^ {2} + a ^ {2} -2ab + b ^ {2} + b ^ {2} - 2bc + c ^ {2} + c ^ {2} \\ & = a ^ {2} + (ab) ^ {2} + (bc) ^ {2} + c ^ {2} \ end {تراز شده} }$
این نتیجه مجموع مربعات است و بنابراین غیر منفی است. و فقط اگر صفر باشد صفر است $\ displaystyle a = b = c = 0$ ، یعنی وقتی z بردار صفر است.
برای هر ماتریس برگشت پذیر واقعی $آ$ ، محصول $\ displaystyle A ^ {\ textf {T}} A$ یک ماتریس قطعی مثبت است. اثبات ساده این است که برای هر بردار غیر صفر است $z$ ، شرایط $\ displaystyle z ^ {\ textf {T}} A ^ {\ Texf {T}} Az = (Az) ^ {\ Texsf {T}} (Az) = \ | آز \ | ^ {2}> 0 }$ از آنجا که غیرقابل برگشت بودن ماتریس است
$آ$ یعنی که $Az \ neq 0.$
مثال $م$ در بالا نشان می دهد که ماتریسی که در آن برخی از عناصر منفی هستند ممکن است هنوز هم قطعی مثبت باشد. در مقابل ، ماتریسی که ورودی های آن همه مثبت است ، مثلاً مثلاً مثبت نیست
$\ displaystyle N = {\ fill bmatrix 1 & 2 \\ 2 & 1 \ end {bmatrix}}،$
برای کدام ${\ displaystyle {\ fill {bmatrix} -1 & 1 \ end {bmatrix} N {\ fill bmatrix} -1 & 1 \ end {bmatrix}} ^ {\ textf T}} = - - 2 <0$

منبع

https://en.wikipedia.org/wiki/Definite_symmetric_matrix

نمای کلی تجزیه LU

توسط علی رضا نقش نیلچی | سه شنبه بیست و چهارم تیر ۱۳۹۹ | 20:26

فاکتورسازی Cholesky

توسط علی رضا نقش نیلچی | سه شنبه بیست و چهارم تیر ۱۳۹۹ | 20:16

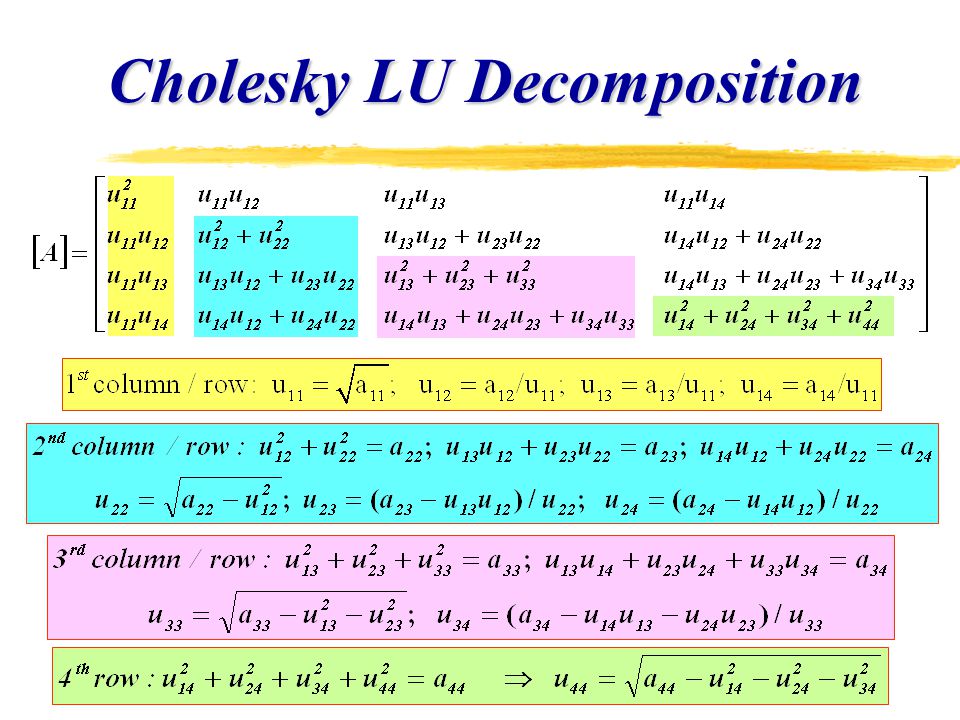
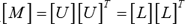تکنیک تجزیه یک ماتریس قطبی مثبت متقارن ( M ) به یک ماتریس مثلثی فوقانی ( U ) و پیوند مزدوج آن ( U ) T به عنوان فاکتورسازی Cholesky شناخته می شود. یعنی . حل عددی معادلات خطی با استفاده از فاکتورسازی Cholesky قابل حل است.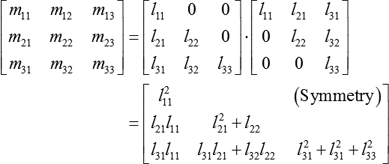

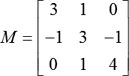نمایندگی کلی تجزیه LU از یک ماتریس 3 × 3 :

مثال:

یک ماتریس مربع را در نظر بگیرید . سپس فاکتورسازی Cholesky (تجزیه) نتیجه می گیرد .

ادامه تجزیه چولسکی

توسط علی رضا نقش نیلچی | دوشنبه بیست و سوم تیر ۱۳۹۹ | 23:17

تجزیه LDL [ ویرایش ]

یک شکل جایگزین ، حذف نیاز به ریشه های مربعی هنگامی که A متقارن باشد ، عامل بندی نامشخص متقارن است [12]

$\ displaystyle {\ fill {تراز شده} \ mathbf {A} = \ mathbf {LDL ^ {\ mathrm {T}} & = {\ fill pmatrix} 1 & 0 & 0 \\ L_ {21} & 1 & 0 \\ L_ {31} & L_ {32} & 1 \\\ end {pmatrix}} {\ fill {pmatrix} D_ {1} & 0 & 0 \\ 0 & D_ {2} & 0 \\ 0 & 0 & D_ {3} \** end {pmatrix}} {\ fill {pmatrix } 1 & L_ {21} & L_ {31} \\ 0 & 1 & L_ {32} \\ 0 & 0 & 1 \\ end {pmatrix}} \\ & = {\ fill pmatrix} D_ {1 && (\ mathrm {متقارن}) \\ L_ {21} D_ {1} & L_ {21} ^ {2} D_ {1} + D_ {2} & \\ L_ {31} D_ {1} & L_ {31} L_ {21} D_ {1} + L_ {32} D_ {2} & L_ {31} ^ {2} D_ {1} + L_ {32} ^ {2} D_ {2} + D_ {3}. \ end {pmatrix}}. \ end {تراز شده} }$

روابط بازگشتی زیر برای ورود D و L اعمال می شود :

$\ displaystyle D_ {j} = A_ {jj} - \ sum _ {k = 1} ^ {j-1} L_ {jk} ^ {2} D_ {k}،$

$left \ displaystyle L_ {ij} = {\ frac {1} {D_ {j}}} \ left (A_ {ij} - \ sum _ {k = 1} ^ {j-1} L_ {ik} L_ {jk D_ {k} \ درست) \ quad {\ متن {برای}} i> j.}$

این کار تا زمانی ادامه می یابد که عناصر مورب تولید شده در D بدون صفر بمانند. تجزیه پس از آن منحصر به فرد است. D و L واقعی اگر واقعی است.

برای ماتریس پیچیده هرمیتی A ، فرمول زیر اعمال می شود:

$\ displaystyle D_ {j} = A_ {jj} - \ sum _ {k = 1} ^ {j-1} L_ {jk} L_ {jk} ^ {*} D_ {k}،}$

$left \ displaystyle L_ {ij} = {\ frac {1} {D_ {j}}} \ left (A_ {ij} - \ sum _ {k = 1} ^ {j-1} L_ {ik} L_ {jk } ^ {*} D_ {k} \ درست) \ quad {\ متن {برای}} i> j.}$

باز هم ، الگوی دسترسی اجازه می دهد تا در صورت دلخواه کل محاسبات در محل انجام شود.

نوع بلوک [ ویرایش ]

هنگامی که در ماتریس نامشخص استفاده می شود ، فاکتورسازی LDL * بدون محور دقیق دقت ناپایدار است. [13] به طور خاص ، عناصر عامل پذیری می توانند خودسرانه رشد کنند. بهبود احتمالی اجرای فاکتورسازی در ماتریسهای زیر بلوک است که معمولاً 2 � 2 است: [14]

$\ displaystyle {\ fill {تراز شده} \ mathbf {A} = \ mathbf {LDL ^ {\ mathrm {T}} & = {\ fill pmatrix} \ mathbf {I} & 0 & 0 \ 0 mathbf {L} _ {21} & \ mathbf {I} & 0 \\\ mathbf {L} _ {31} & \ mathbf {L} _ {32} & \ mathbf {I} \\\ end pmatrix}} {\ fill {pmatrix \ mathbf {D} _ {1} & 0 & 0 \\ 0 & \ mathbf {D} _ {2} & 0 \\ 0 & 0 & \ mathbf {D} _ {3} \** end {pmatrix}} {\ fill {pmatrix} \ mathbf {I} & \ mathbf {L} _ {21} ^ {\ mathrm {T}} & \ mathbf {L} _ {31} ^ {\ mathrm {T}} \\ 0 & \ mathbf {I} & \ mathbf {L} _ {32} ^ {\ mathrm {T} \ \\ 0 & 0 & \ mathbf {I} \\\ end {pmatrix}} \\ & = {\ start pmatrix} \ mathbf {D} _ { 1 }&& (\ mathrm {متقارن) \\\ mathbf {L} _ {21 \ mathbf {D} _ {1} & \ mathbf {L} _ {21} \ mathbf {D} _ {1} \ mathbf {L} _ {21} ^ {\ mathrm {T}} + \ mathbf {D} _ {2} & \\\ mathbf {L} _ {31} \ mathbf {D} _ {1} &\ mathbf {L} _ {31} \ mathbf {D} _ {1} \ mathbf {L} _ {21} ^ {\ mathrm {T}} + \ mathbf {L} _ {32} \ mathbf {D} _ {2} & \ mathbf {L} _ {31} \ mathbf {D} _ {1} \ mathbf {L} _ {31} ^ {\ mathrm {T}} + \ mathbf {L} _ {32} \ mathbf {D} _ {2} \ mathbf {L} _ {32} ^ {\ mathrm {T}} + \ mathbf {D} _ {3} \ end {pmatrix}}، \ end {تراز شده}}}$

که در آن هر عنصر در ماتریس های بالا یک زیرمجاز مربع است. از این ، این روابط بازگشتی مشابه به دنبال دارند:

$\ displaystyle \ mathbf {D} _ {j} = \ mathbf {A} _ {jj} - \ sum _ {k = 1} ^ {j-1} \ mathbf {L} _ {jk} \ mathbf {D _ {k} \ mathbf {L} _ {jk} ^ {\ mathrm {T}}،$

$\ displaystyle \ mathbf {L} _ {ij} = \ left (\ mathbf {A} _ {ij} - \ sum _ {k = 1} ^ {j-1 \ mathbf {L} _ {ik} \ mathbf {D} _ {k} \ mathbf {L} _ {jk} ^ {\ mathrm {T}} \ Right) \ mathbf {D} _ {j} ^ {- 1}.$

این شامل محصولات ماتریس و وارونگی صریح است ، بنابراین اندازه بلوک عملی را محدود می کند.

به روزرسانی تجزیه [ ویرایش ]

وظیفه ای که اغلب در عمل بوجود می آید این است که فرد باید تجزیه Cholesky را به روز کند. در جزییات بیشتر ، یک نفر قبلاً تجزیه Cholesky را محاسبه کرده است

$\ displaystyle \ mathbf {A} = \ mathbf {L} \ mathbf {L} ^ {*}}$ برخی از ماتریس

$\ mathbf {A$ سپس یکی ماتریس را تغییر می دهد

$\ mathbf {A$ به نوعی بگویید $\ tilde {\ mathbf {A}}$ ، و یکی می خواهد تجزیه Cholesky ماتریس به روز شده را محاسبه کند: $\ tilde {\ mathbf {A}}} = {\ tilde {\ mathbf {L}}} {\ tilde {\ mathbf {L}}} ^ {*}$ . حال این سؤال مطرح است که آیا می توان از تجزیه چولسکی استفاده کرد؟

$\ mathbf {A$ که قبل از محاسبه برای تجزیه Cholesky محاسبه شد $\ tilde {\ mathbf {A}}$ .

مرتباً یک به روزرسانی [ ویرایش ]

مورد خاص ، که در آن ماتریس به روز شده است $\ tilde {\ mathbf {A}}$ مربوط به ماتریس است

$\ mathbf {A$ توسط $\ tilde {\ mathbf {A}}} = \ mathbf {A} + \ mathbf x} \ mathbf x} ^ {*}$ ، به عنوان یک به روزرسانی درجه یک شناخته می شود .

در اینجا یک تابع کوچک [15] با نحوی Matlab نوشته شده است که یک بروزرسانی درجه یک را تحقق می بخشد:

تابع  [L] = cholupdate ( L ، x ) 
    n  =  طول ( x )؛
    برای k = 1: n
        r  =  sqrt ( L ( k ،  k ) ^ 2     x ( k ) ^ 2 )؛ 
        c  =  r  /  L ( k ،  k )؛ 
        s  =  x ( k )  /  L ( k ،  k )؛ 
        L ( k ،  k )  =  r ؛
        اگر k 
            L (( k   1 ): n ،  k )  =  ( L (( k   1 ): n ،  k )     s  *  x (( k   1 ): n ))  /  c ؛ 
            x (( k   1 ): n )  =  c  *  x (( k   1 ): n )  -  s  *  L ((k   1 ): n ،  k )؛
        پایان 
پایان    
پایان

رتبه بندی یک نزولی [ ویرایش ]

downdate رتبه یک شبیه به یک رتبه یک به روز رسانی است، به جز که علاوه بر تفریق است جایگزین: $\ tilde {\ mathbf {A}}} = \ mathbf {A} - \ mathbf {x} \ mathbf x} ^ {*}$ . این تنها در صورت ماتریس جدید کار می کند $\ tilde {\ mathbf {A}}$ هنوز قطعی مثبت است

کد برای به روزرسانی درجه یک که در بالا نشان داده شده است به راحتی می تواند برای انجام یک نزولی رتبه یک باشد: یکی فقط نیاز به جایگزینی دو اضافات در انتساب به r و L((k 1):n, k) تفریق دارد.

اضافه کردن و حذف سطرها و ستون ها [ ویرایش ]

در صورت داشتن ماتریس مشخص و متقارن و مثبت $\ displaystyle \ mathbf {A}$ به صورت بلوک به عنوان نشان داده شده است

$\ displaystyle \ mathbf {A = {\ آغاز {pmatrix} \ mathbf {A} _ {11} & \ mathbf {A} _ {13 \\\ mathbf {A} _ {13} ^ {\ mathrm { T}} & \ mathbf {A} _ {33} \\\ end {pmatrix}}$

و عامل بالایی آن Cholesky است

$\ displaystyle \ mathbf {L} = {\ fill {pmatrix \ mathbf {L} _ {11} & \ mathbf {L} _ {13 \\ 0 & \ mathbf {L} _ {33} \** end {pmatrix} ،}$

سپس برای یک ماتریس جدید $\ tilde {\ mathbf {A}}$ ، که همان است $\ displaystyle \ mathbf {A}$ اما با درج ردیف ها و ستون های جدید ،

$\ displaystyle {\ شروع {تراز شده} {\ tilde {\ mathbf {A}}} & = {\ آغاز {pmatrix} \ mathbf {A _ {11} & \ mathbf {A} _ {12} & \ mathbf {A} _ {13} \\\ mathbf {A} _ {12} ^ {\ mathrm {T}} & \ mathbf {A} _ {22 & \ mathbf {A} _ {23} \\\ mathbf A} _ {13} ^ {\ mathrm {T}} & \ mathbf {A} _ {23} ^ {\ mathrm {T}} & \ mathbf {A} _ {33} \** end {pmatrix} } \ end {تراز شده}}}$

ما علاقه مند به یافتن فاکتورسازی Cholesky از $\ tilde {\ mathbf {A}}$ ، که ما آن را صدا می کنیم $\ displaystyle \ tilde {\ mathbf {S}}}$ بدون محاسبه مستقیم کل تجزیه.

$\ displaystyle {\ شروع {تراز شده} {\ tilde {\ mathbf {S}}} & = {\ آغاز {pmatrix} \ mathbf {S} _ {11} & \ mathbf {S} _ {12} & \ mathbf {S} _ {13} \\ 0 & \ mathbf {S} _ {22} & \ mathbf {S} _ {23} \\ 0 & 0 & \ mathbf {S} _ {33 \\\ end {pmatrix}. \ end {تراز شده}}}$

نوشتن $\ displaystyle \ mathbf {A} \ setminus \ mathbf {b}$ برای راه حل

$\ displaystyle \ mathbf {A} \ mathbf {x} = \ mathbf {b$ ، که می توان به راحتی برای ماتریس های مثلثی پیدا کرد ، و $\ displaystyle \ متن {chol}} (\ mathbf {M})}$ برای تجزیه Cholesky از ${\ mathbf M$ روابط زیر را می توان یافت:

$\ displaystyle {\ شروع {تراز شده} \ mathbf {S} _ {11} & = \ mathbf {L} _ {11} ، \\\ mathbf {S} _ {12} & = \ mathbf {L} _ { 11} ^ {\ mathrm {T}} \ setminus \ mathbf {A} _ {12}، \\\ mathbf {S} _ {13} & = = mathbf {L} _ {13}، \\\ mathbf { S} _ {22} & = {\ text {chol}} (\ mathbf {A} _ {22} - \ mathbf {S} _ {12} ^ {\ mathrm {T}} \ mathbf {S} _ 12}) ، \\\ mathbf {S} _ {23} & = \ mathbf {S} _ {22} ^ {\ mathrm {T}} \ setminus (\ mathbf {A} _ {23} - \ mathbf { S} _ {12} ^ {\ mathrm {T}} \ mathbf {S} _ {13})، \\\ mathbf {S} _ {33} & = {\ text {chol}} (\ mathbf {L } _ {33} ^ {\ mathrm {T}} \ mathbf {L} _ {33} - \ mathbf {S} _ {23} ^ {\ mathrm {T}} \ mathbf {S} _ {23}) . \\\ end {تراز شده}}}$

در صورت تنظیم مناسب ابعاد سطر و ستون (از جمله به صفر) ممکن است از این فرمولها برای تعیین فاکتور چولسکی پس از درج سطرها یا ستونها در هر موقعیت استفاده شود. مشکل معکوس ، وقتی که داریم

با تجزیه شناخته شده Cholesky

و آرزو می کنیم فاکتور چولسکی را تعیین کنیم

$\ displaystyle {\ fill {تراز شده} \ mathbf {L} & = {\ fill pmatrix \ mathbf {L} _ {11} & \ mathbf {L} _ {13} \\ 0 & \ mathbf {L} _ {33} \\\ end {pmatrix}} \ end {تراز شده}}$

ماتریس $\ displaystyle \ mathbf {A}$ با حذف ردیف ها و ستون ها ،

$\ displaystyle {\ fill {تراز شده} \ mathbf {A} & = {\ fill pmatrix} \ mathbf {A _ {11} & \ mathbf {A} _ {13} \\\ mathbf {A} _ { 13} ^ {\ mathrm {T}} & \ mathbf {A} _ {33} \\\ end {pmatrix}}، \ end {تراز شده}}$

قوانین زیر را ارائه می دهد:

$\ displaystyle {\ شروع {تراز شده} \ mathbf {L} _ {11} & = \ mathbf {S} _ {11}، \\\ mathbf {L} _ {13} & = \ mathbf {S} _ 13} ، \\\ mathbf {L} _ {33} & = {\ text {chol}} (\ mathbf {S} _ {33} + \ mathbf {S} _ {23} ^ {\ mathrm {T } \ mathbf {S} _ {23}). \ end {تراز شده}}}$

توجه کنید که معادلات فوق که شامل یافتن تجزیه Cholesky یک ماتریس جدید هستند ، همه از این شکل هستند

$\ displaystyle {\ tilde {\ mathbf {A}}} = \ mathbf {A} \ pm \ mathbf {x} \ mathbf {x} ^ {*}}$ ، که به آنها اجازه می دهد تا با استفاده از روشهای به روزرسانی و downdate که به تفصیل در قسمت قبلی شرح داده شده ، محاسبه شوند. [16]

اثبات ماتریسهای نیمه قطعی مثبت [ ویرایش ]

اثبات با محدود کردن استدلال [ ویرایش ]

الگوریتم های فوق نشان می دهد که هر ماتریس مشخص مثبت است $\ mathbf {A$ تجزیه Cholesky است. این نتیجه را می توان با یک استدلال محدود به پرونده نیمه نهایی قطعی مثبت افزایش داد. این استدلال کاملاً سازنده نیست ، یعنی هیچ محاسبه ای صریح برای محاسبه فاکتورهای چولسکی ارائه نمی دهد.

اگر $\ mathbf {A$ هست یک $n \ n n$ ماتریس نیمه قطعی مثبت ، سپس دنباله $\ displaystyle \ left (\ mathbf {A} _ {k} \ Right) _ {k}: = \ left (\ mathbf {A} + {\ frac {1} {k}} \ mathbf {I} _ { n} \ درست) _ {k}}$ متشکل از ماتریس های مثبت مثبت است . (این یک نتیجه فوری مثلاً قضیه نقشه برداری طیفی برای حساب کارکردی چند جمله ای است.) همچنین ،

$\ displaystyle \ mathbf {A} _ {k} \ rightarrow \ mathbf {A} \ quad {\ متن {برای}} \ quad k \ rightarrow \ infty$

در هنجار اپراتور . از مورد قطعی مثبت ، هر کدام

${\ mathbf {A}} _ {k}$ تجزیه Cholesky است $\ displaystyle \ mathbf {A} _ {k} = \ mathbf {L} _ {k} \ mathbf {L} _ {k} ^ {*}}$ . براساس ویژگی هنجار اپراتور ،

$\ displaystyle \ | \ mathbf {L} _ {k} \ | ^ {2} \ geq \ | \ mathbf {L} _ {k} \ mathbf {L} _ {k} ^ {*} \ | = \ | \ mathbf {A} _ {k} \ | \،.$

بنابراین ${\ نمایش صفحه \ سمت چپ (\ mathbf {L} _ {k} \ سمت راست) _ {k}}$ یک مجموعه محدود در فضای Banach اپراتورها است ، بنابراین نسبتاً جمع و جور است (زیرا فضای بردار زیرین متناهی است). در نتیجه ، این یک پیامد همگرایی دارد ، که از آن نیز یاد شده است ${\ نمایش صفحه \ سمت چپ (\ mathbf {L} _ {k} \ سمت راست) _ {k}}$ ، با حد مجاز $\ mathbf {L$ . به راحتی قابل بررسی است که این $\ mathbf {L$ دارای خواص مورد نظر ، یعنی $\ displaystyle \ mathbf {A} = \ mathbf {L} \ mathbf {L} ^ {*}}$ و

$\ mathbf {L$ مثلث پایین با ورودی های مورب غیر منفی است: برای همه $ایکس$ و $ی$ ،

$\ displaystyle \ langle \ mathbf {A} x، y \ rangle = \ left \ langle \ lim \ mathbf {A} _ {k} x، y \ Right \ rangle = \ langle \ lim \ mathbf {L} _ { k} \ mathbf {L} _ {k} ^ {*} x، y \ rangle = \ langle \ mathbf {L} \ mathbf {L} ^ {*} x، y \ rangle \ ،.}$

از این رو، $\ displaystyle \ mathbf {A} = \ mathbf {L} \ mathbf {L} ^ {*}}$ . از آنجا که فضای بردار زیرین محدود است ، تمام توپولوژی های موجود در فضای اپراتورها معادل هستند. بنابراین ${\ نمایش صفحه \ سمت چپ (\ mathbf {L} _ {k} \ سمت راست) _ {k}}$ تمایل دارد

$\ mathbf {L$ به معنای هنجار ${\ نمایش صفحه \ سمت چپ (\ mathbf {L} _ {k} \ سمت راست) _ {k}}$ تمایل دارد $\ mathbf {L$ ورودی این به نوبه خود نشان می دهد که ، از هر یک $\ displaystyle \ mathbf {L} _ {k}}$ مثلث پایین با ورودی های مورب غیر منفی است ، $\ mathbf {L$ هم هست

اثبات تجزیه QR [ ویرایش ]

اجازه دهید $\ mathbf {A$ یک ماتریس نیمه قطعی مثبت هرمی باشد. سپس می توان آن را به عنوان محصولی از ماتریس ریشه مربع آن نوشت ، $\ displaystyle \ mathbf {A} = \ mathbf {B} \ mathbf {B} ^ {*}}$ . اکنون می توان تجزیه QR را نیز اعمال کرد $\ displaystyle \ mathbf {B} ^ {*}}$ ، منجر به $\ displaystyle \ mathbf {B} ^ {*} = \ mathbf {Q} \ mathbf {R}}$ ، جایی که $\ mathbf {Q$ واحد است و $\ mathbf {R$ مثلث فوقانی است درج تجزیه در بازده اصلی برابری

$\ displaystyle A = \ mathbf {B} \ mathbf {B} ^ {*} = (\ mathbf {QR}) ^ {*} \ mathbf {QR} = \ mathbf {R} ^ {*} \ mathbf {Q } ^ {*} \ mathbf {QR} = \ mathbf {R} ^ {*} \ mathbf {R}$ . تنظیمات

$\ displaystyle \ mathbf {L} = \ mathbf {R} ^ {*}$ اثبات را کامل می کند.

تعمیم [ ویرایش ]

فاکتورسازی Cholesky را می توان [با استناد به نیاز ] برای ماتریس (نه لزوما محدود) با ورودی اپراتور تعمیم داد . اجازه دهید

$\ {{\ mathcal {H}} _ {n} \}$ دنباله ای از فضاهای هیلبرت باشید . ماتریس اپراتور را در نظر بگیرید

$\ mathbf {A} = {\ آغاز {bmatrix} \ mathbf {A} _ {11} & \ mathbf {A _ {12} & \ mathbf {A} _ {13} & \؛ \\\ mathbf {A _ {12} ^ {*} & \ mathbf {A} _ {22} & \ mathbf {A} _ {23} & \؛ \\\ mathbf {A} _ {13} ^ {*} & \ mathbf {A} _ {23} ^ {*} & \ mathbf {A} _ {33} & \؛ \\\؛ & \؛ & \؛ & \ ddots \ end {bmatrix}$

اقدام به مبلغ مستقیم

$\ displaystyle {\ mathcal {H}} = \ bigoplus _ {n} {\ mathcal {H}} _ {n،$

جایی که هر کدام

$\ mathbf {A} _ {ij}: {\ mathcal {H}} _ {j} \ rightarrow {\ mathcal {H}} _ {i}$

یک اپراتور محدود است . اگر A مثبت باشد (semidefinite) به این معنا که برای همه k K محدود و برای هر

$\ displaystyle h \ in \ bigoplus _ {n = 1} ^ {k} {\ mathcal {H}} _ {k}،$

ما داریم $\ langle h، \ mathbf {A} h \ rangle \ geq 0$ ، سپس یک ماتریس اپراتور مثلثی L پایین وجود دارد به گونه ای که A = LL *. همچنین می توان ورودی های مورب L را مثبت دانست.

منبع

https://en.wikipedia.org/wiki/Cholesky_decomposition#

مطالب قدیمی تر

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی

ادامه فضای بردار توپولوژیکی

انواع [ ویرایش ]

فضای دوگانه [ ویرایش ]

خواص [ ویرایش ]

خواص حفظ شده توسط اپراتورهای تنظیم شده [ ویرایش ]

ادامه فضای بردار توپولوژیکی

توپولوژی بردار نهایی [ ویرایش ]

فضاهای بردار ضرب [ ویرایش ]

ساختار توپولوژیکی [ ویرایش ]

مفاهیم محلی [ ویرایش ]

فضای بردار توپولوژیکی

فهرست

تعریف [ ویرایش ]

راه های تعریف توپولوژی بردار [ ویرایش ]

مثالها [ ویرایش ]

عملگر خطی محدود

فهرست

اپراتورهای محدود در فضاهای بردار توپولوژیکی [ ویرایش ]

فضاهای بورنولوژیکی [ ویرایش ]

خصوصیات اپراتورهای خطی محدود [ ویرایش ]

عملگرهای خطی محدود شده بین فضاهای نرمال [ ویرایش ]

معادل محدودیت و استمرار [ ویرایش ]

خصوصیات بیشتر [ ویرایش ]

مثالها [ ویرایش ]

اپراتورهای خطی بدون مرز [ ویرایش ]

ویژگی های فضای اپراتورهای خطی محدود [ ویرایش ]

گرانش ساختاری

فهرست

نظریه های مربع ویل [ ویرایش ]

نظریه های چهار مشتق [ ویرایش ]

وحدت سازه با مدل استاندارد [ ویرایش ]

منبع

شعاع طیفی

فهرست

ماتریس [ ویرایش ]

نمودارها [ ویرایش ]

حد بالایی [ ویرایش ]

مرزهای بالا برای شعاع طیفی یک ماتریس [ ویرایش ]

مرزهای بالا برای شعاع طیفی از یک نمودار [ ویرایش ]

دنباله قدرت [ ویرایش ]

قضیه [ ویرایش ]

اثبات قضیه [ ویرایش ]

فرمول گلفند [ ویرایش ]

قضیه [ ویرایش ]

اثبات [ ویرایش ]

نتیجه گیری های گلفند [ ویرایش ]

مثال [ ویرایش ]

عملگرهای خطی محدود [ ویرایش ]

منابع

روش ژاکوبی

فهرست

توضیحات [ ویرایش ]

الگوریتم [ ویرایش ]

همگرایی [ ویرایش ]

مثال [ ویرایش ]

مثال دیگر [ ویرایش ]

مثالی با استفاده از پایتون و نامپی [ ویرایش ]

روش ژاکوبی وزنی [ ویرایش ]

همگرایی در مورد قطعی مثبت متقارن [ ویرایش ]

روش گاوس-سییدل

فهرست

توضیحات [ ویرایش ]

بحث [ ویرایش ]

همگرایی [ ویرایش ]

الگوریتم [ ویرایش ]

مثالها [ ویرایش ]

نمونه ای از نسخه ماتریس [ ویرایش ]

مثال دیگر برای نسخه ماتریس [ ویرایش ]

نمونه ای از نسخه معادله [ ویرایش ]

مثالی با استفاده از Python و NumPy [ ویرایش ]

برنامه ای برای حل خودسرانه شماره. معادلات با استفاده از Matlab [ ویرایش ]

تبدیل ویل

کمیت تغییر شکل [ ویرایش ]

کلیات [ ویرایش ]

تبدیل ویل

فرمول اساسی [ ویرایش ]

در نمایه موقعیت [ ویرایش ]

نقشه معکوس [ ویرایش ]