5-مختصات کروی

توسط علی رضا نقش نیلچی | دوشنبه نهم اسفند ۱۴۰۰ | 12:4

تعمیم [ ویرایش ]

همچنین می توان با استفاده از نسخه اصلاح شده مختصات کروی با بیضی ها در مختصات دکارتی مقابله کرد.

فرض کنید P یک بیضی مشخص شده توسط مجموعه سطح باشد

$ax^{2}+by^{2}+cz^{2}=d.$

مختصات کروی اصلاح شده یک نقطه در P در کنوانسیون ISO (یعنی برای فیزیک: شعاع r ، تمایل θ ، آزیموت φ ) را می توان از مختصات دکارتی آن ( x ، y ، z ) با فرمول به دست آورد.

${\begin{aligned}x&={\frac {1}{\sqrt {a}}}r\sin \theta \,\cos \varphi ,\\y&={\frac {1}{\sqrt {b}}}r\sin \theta \,\sin \varphi ,\\z&={\frac {1}{\sqrt {c}}}r\cos \theta ,\\r^{2}&= ax^{2}+by^{2}+cz^{2}.\end{aligned}}$

یک عنصر حجم بینهایت کوچک توسط

$\mathrm {d} V=\left|{\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}\right|\,dr\,d \theta \,d\varphi ={\frac {1}{\sqrt {abc}}}r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \, \mathrm {d} \varphi ={\frac {1}{\sqrt {abc}}}r^{2}\,\mathrm {d} r\,\mathrm {d} \Omega .$

ضریب ریشه مربع از خاصیت دترمینان می آید که اجازه می دهد یک ثابت از یک ستون خارج شود:

${\begin{vmatrix}ka&b&c\\kd&e&f\\kg&h&i\end{vmatrix}}=k{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}.$

ادغام و تمایز در مختصات کروی [ ویرایش ]

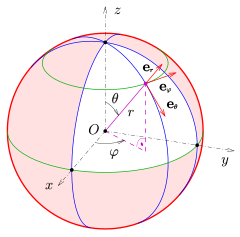
بردارهای واحد در مختصات کروی

معادلات زیر (Iyanaga 1977) فرض می‌کنند که colatitude θ تمایل از محور z (قطبی) است (مبهم است زیرا x ، y ، و z متقابل نرمال هستند)، همانطور که در قرارداد فیزیک مورد بحث قرار گرفت.

عنصر خط برای جابجایی بینهایت کوچک از ( r ، θ ، φ ) به ( r + d r ، θ + d θ ، φ + d φ ) است.

$\mathrm {d} \mathbf {r} =\mathrm {d} r\,{\hat {\mathbf {r} }}+r\,\mathrm {d} \theta \,{\hat { \boldsymbol {\theta }}}+r\sin {\theta }\,\mathrm {d} \varphi \,\mathbf {\hat {\boldsymbol {\varphi }}} ,$

جایی که

${\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \cos \varphi \,{\hat {\mathbf {x} }}+\sin \theta \sin \varphi \,{\hat {\mathbf {y} }}+\cos \theta \,{\hat {\mathbf {z} }},\\{\hat {\boldsymbol {\theta }}}&= \cos \theta \cos \varphi \,{\hat {\mathbf {x} }}+\cos \theta \sin \varphi \,{\hat {\mathbf {y} }}-\sin \theta \, {\hat {\mathbf {z} }},\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi \,{\hat {\mathbf {x} }}+\cos \ varphi \,{\hat {\mathbf {y} }}\end{تراز شده}}$

بردارهای واحد متعامد محلی به ترتیب در جهت افزایش r , θ , و φ هستند و x̂ , ŷ و ẑ بردارهای واحد در مختصات دکارتی هستند. تبدیل خطی به این سه گانه مختصات راست دست یک ماتریس چرخشی است .

$R={\begin{pmatrix}\sin \theta \cos \varphi &\sin \theta \sin \varphi &\cos \theta \\\cos \theta \cos \varphi &\cos \theta \sin \varphi &-\sin \theta \\-\sin \varphi &\cos \varphi &0\end{pmatrix}}.$

این تبدیل از کروی به دکارتی را می دهد، برعکس آن توسط معکوس آن به دست می آید. نکته: ماتریس یک ماتریس متعامد است، یعنی معکوس آن به سادگی جابجایی آن است.

بنابراین، بردارهای واحد دکارتی با بردارهای واحد کروی مرتبط هستند:

${\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}={\begin {bmatrix}\sin \theta \cos \phi &\cos \theta \cos \phi &-\sin \phi \\\sin \theta \sin \phi &\cos \theta \sin \phi &\cos \phi \\\cos \theta &-\sin \theta &0\end{bmatrix}}{\begin{bmatrix}{\boldsymbol {\hat {r}}}\\{\boldsymbol {\hat {\theta }}} \\{\boldsymbol {\hat {\phi }}}\end{bmatrix}}$

شکل کلی فرمول برای اثبات عنصر خط دیفرانسیل، [5] است.

$\mathrm {d} \mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial x_{i}}}\,\mathrm {d} x_{ i}=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|{\frac {\frac {\partial \mathbf {r} }{\partial x_{i}}}{\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|}}\,\mathrm {d} x_{i }=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|\,\mathrm {d} x_{i}\,{\ کلاه {\boldsymbol {x}}}_{i}،$

یعنی تغییر در $\mathbf {r}$ به تغییرات فردی مربوط به تغییرات در مختصات فردی تجزیه می شود.

برای اعمال این مورد در مورد حاضر، باید نحوه محاسبه را محاسبه کرد $\mathbf {r}$ با هر یک از مختصات تغییر می کند. در کنوانسیون های مورد استفاده،

$\mathbf {r} ={\begin{bmatrix}r\sin \theta \,\cos \varphi \\r\sin \theta \,\sin \varphi \\r\cos \theta \end{bmatrix }}.$

بدین ترتیب،

${\frac {\partial \mathbf {r} }{\partial r}}={\begin{bmatrix}\sin \theta \,\cos \varphi \\\sin \theta \,\sin \varphi \\\cos \theta \end{bmatrix}},\quad {\frac {\partial \mathbf {r} }{\partial \theta }}={\begin{bmatrix}r\cos \theta \,\cos \varphi \\r\cos \theta \,\sin \varphi \\-r\sin \theta \end{bmatrix}},\quad {\frac {\partial \mathbf {r} }{\partial \varphi } }={\begin{bmatrix}-r\sin \theta \,\sin \varphi \\r\sin \theta \,\cos \varphi \\0\end{bmatrix}}.$

ضرایب مورد نظر، بزرگی این بردارها هستند: [5]

$\left|{\frac {\partial \mathbf {r} }{\partial r}}\right|=1,\quad \left|{\frac {\partial \mathbf {r} }{\partial \theta }}\right|=r,\quad \left|{\frac {\partial \mathbf {r} }{\partial \varphi }}\right|=r\sin \theta .$

عنصر سطحی که از θ تا θ + d θ و φ تا φ + d φ بر روی یک سطح کروی در شعاع r (ثابت) را پوشانده است.

$\mathrm {d} S_{r}=\left\|{\frac {\partial r{\hat {\mathbf {r} }}}{\partial \theta }}\times {\frac {\ جزئی r{\hat {\mathbf {r} }}}{\partial \varphi }}\right\|\mathrm {d} \theta \,\mathrm {d} \varphi =r^{2}\sin \ تتا \,\ mathrm {d} \theta \,\mathrm {d} \varphi ~.$

بنابراین زاویه جامد دیفرانسیل است

$\mathrm {d} \Omega ={\frac {\mathrm {d} S_{r}}{r^{2}}}=\sin \theta \,\mathrm {d} \theta \,\ ریاضی {d} \varphi .$

عنصر سطح در سطحی با زاویه قطبی θ ثابت (یک مخروط با راس مبدأ) است

$\mathrm {d} S_{\theta }=r\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} r.$

عنصر سطح در سطحی با آزیموت φ ثابت (یک نیمه صفحه عمودی) است

$\mathrm {d} S_{\varphi }=r\,\mathrm {d} r\,\mathrm {d} \theta .$

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی