نقشه های یکنواخت مداوم [ ویرایش ]
نقشه


هر نقشه یکنواخت مداوم 

نقشه های یکنواخت پیوسته توالی های کوشی را به داخل تبدیل می کنند 


نقشه ها و انقباضات مداوم لیپشیتس [ ویرایش ]
مقاله اصلی: تداوم لیپشیتس
با توجه به یک عدد واقعی

هر نقشه مداوم با لیپشیتس به طور یکنواخت مداوم است ، اما عکس العمل به طور کلی درست نیست.
اگر








ایزومتری [ ویرایش ]
نقشه
ایزومتری همیشه م injثر است . تصویر یک مجموعه جمع و جور یا کامل در زیر ایزومتری به ترتیب فشرده یا کامل است. با این حال اگر همسان است پوشا ، سپس تصویر از یک بسته (یا باز) مجموعه نیاز نیست بسته شود (یا باز).
شبه ایزومتری [ ویرایش ]
نقشه


و یک ثابت 



توجه داشته باشید که شبه ایزومتری برای ادامه دار بودن لازم نیست. شبه ایزومتری ها "ساختار در مقیاس بزرگ" فضاهای متریک را مقایسه می کنند. آنها در تئوری گروه هندسی در رابطه با کلمه متریک استفاده می کنند .
مفاهیم معادل سازی فضای متریک [ ویرایش ]
با توجه به دو فضای متریک 

- آنها به نام homeomorphic (توپولوژیکی ریخت) اگر وجود داشته باشد وجود دارد همسانریختی بین آنها (به عنوان مثال، یک پوشا و یکبهیک مداوم در هر دو جهت).
- آنها به نام uniformic (یکنواخت ریخت) اگر وجود داشته باشد وجود دارد ریخت یکنواخت بین آنها (به عنوان مثال، یک پوشا و یکبهیک یکنواخت در هر دو جهت مداوم).
- آنها به نام ایزومتریک اگر وجود داشته باشد وجود دارد دوسویی همسان بین آنها. در این حالت ، دو فضای متریک اساساً یکسان هستند.
- اگر شبه ایزومتری بین آنها وجود داشته باشد ، آنها را شبه ایزومتریک می نامند .
خواص توپولوژیکی [ ویرایش ]
فضاهای متریک پارامپکتاکتیو هستند [7] فضاهای هاوسدورف [8] و از این رو طبیعی هستند (در واقع کاملاً طبیعی هستند). یک پیامد مهم این است که هر فضای متریک پارتیشن های وحدت را می پذیرد و هر تابع با ارزش واقعی پیوسته که در یک زیر مجموعه بسته از یک فضای متریک تعریف شده است ، می تواند به یک نقشه مداوم در کل فضا گسترش یابد (قضیه پسوند Tietze ). همچنین درست است که هر نقشه پیوسته لیپشیتس با ارزش واقعی که در زیرمجموعه ای از یک فضای متریک تعریف شده است ، می تواند به یک نقشه پیوسته لیپشیتس در کل فضا گسترش یابد.
فضاهای متریک ابتدا قابل شمارش هستند زیرا می توان از توپهایی با شعاع منطقی به عنوان پایه محله استفاده کرد.
توپولوژی متریک در یک فضای متریک 



فاصله بین نقاط و مجموعه ها ؛ فاصله هاوسدورف و معیار Gromov [ ویرایش ]
یک روش ساده برای ساختن تابعی که یک نقطه را از یک مجموعه بسته جدا می کند (همانطور که برای یک فضای کاملاً منظم لازم است) در نظر گرفتن فاصله بین نقطه و مجموعه است . اگر








سپس


که به ویژه نشان می دهد که نقشه
با توجه به دو زیر مجموعه 




به طور کلی ، فاصله هاوسدورف
فاصله هاوسدورف




سپس می توان فاصله Gromov – Hausdorff را بین هر دو فضای متریک با در نظر گرفتن حداقل فاصله Hausdorff از نسخه های تعبیه شده ایزومتریک از دو فضا تعریف کرد. با استفاده از این فاصله ، کلاس همه فضاهای متریک جمع و جور در نوع خود به یک فضای متریک تبدیل می شود.
فضاهای متریک محصول [ ویرایش ]
اگر 



و توپولوژی ناشی از آن با توپولوژی محصول موافق است . با معادل سازی هنجارها در ابعاد محدود ، اگر یک معیار معادل بدست آید

به همین ترتیب ، یک محصول قابل شمارش از فضاهای متریک را می توان با استفاده از متریک زیر بدست آورد
یک محصول غیرقابل شمارش از فضاهای متریک لازم نیست قابل اندازه گیری باشد. مثلا،
تداوم مسافت [ ویرایش ]
در مورد یک فضای واحد 



فضاهای متریک کمیت [ ویرایش ]
اگر M یک فضای متریک با متریک است



![[ایکس]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![[y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f637a17dac262ee0fc8d58e31d08ca3ebe5a0fed)
جایی که حداقل از تمام توالی های محدود گرفته می شود

![[q_i] = [p_ {i + 1}] ، i = 1،2 ، \ dots ، n-1](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa921d9eb1c7739ebdea8b30697d4376b5236ea9)
![d '([x] ، [y]) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f0686af91a21fdf1ed41059fa39ffbbe883bd4f)
![[x] = [سال]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a)

معیار ضریب 






![\ overline {f} ([x]) = f (x)](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa40e344823d6033e5b82eaf6f31f3a562c6c9c6)
یک فضای توپولوژیکی ترتیبی است اگر و فقط اگر نصف یک فضای متریک باشد. [9]
تعمیم فضاهای متریک [ ویرایش ]
- هر فضای متریک به صورت طبیعی یک فضای یکنواخت است و هر فضای یکنواختی به طور طبیعی یک فضای توپولوژیک است . بنابراین می توان فضاهای یکنواخت و توپولوژیک را تعمیم فضاهای متریک دانست.
- اگر اولین تعریف از فضای متریک را در بالا در نظر بگیریم و نیاز دوم را آرام کنیم ، به مفاهیم یک فضای شبه سنجی یا یک فضای متریک دررفتگی می رسیم . [10] اگر سوم یا چهارم را حذف کنیم ، به یک فضای نیمه سنجی ، یا یک فضای نیم متری می رسیم .
- اگر تابع فاصله در خط عدد توسعه یافته واقعی مقادیر را بدست آورد
، اما در غیر این صورت هر چهار شرط را برآورده می کند ، سپس آن را یک متریک توسعه یافته و فضای مربوطه را an می نامند
فضای -metric . اگر تابع فاصله در برخی از مجموعه های مناسب (مناسب) مقادیر را بدست آورد (و نابرابری مثلث بر این اساس تنظیم شود) ، ما به مفهوم فوق متری تعمیم یافته خواهیم رسید . [10]
- فضاهای رویکرد ، تعمیم فضاهای متریک ، براساس فاصله از نقطه به نقطه ، به جای فاصله از نقطه به نقطه است.
- فضای تداوم یک کلیت از فضاهای متریک و posets ، که می تواند مورد استفاده قرار گیرد برای متحد کردن مفاهیم فضاهای متریک و دامنه .
- یک فضای متریک جزئی در نظر گرفته شده است تا حداقل تعمیم مفهوم فضای متریک باشد ، به این ترتیب که فاصله هر نقطه از خود دیگر لزوماً صفر نیست. [11]
فضاهای متریک به عنوان دسته های غنی شده [ ویرایش ]
مجموعه سفارش داده شده 
morphism 







- تنظیم
- برای هر
تنظیم
- شکل ظاهری ترکیب
شکل منحصر به فرد در خواهد بود
از نابرابری مثلث داده شده است
- شکل شناسی هویت
مورفيسم منحصر به فرد خواهد بود از اين واقعيت
.
- از آنجا که
یک پیام است ، تمام نمودارهایی که برای یک گروه غنی شده به طور خودکار رفت و آمد می کنند.
مقاله FW Lawvere را که در زیر لیست شده است مشاهده کنید.
همچنین به [ ویرایش ] مراجعه کنید
- مشکل الکساندروف – راسیاس
- دسته فضاهای متریک
- فضای کلاسیک وینر
- انقباض نقشه - عملکرد کاهش فاصله بین تمام نقاط
- واژه نامه هندسه متریک و متریک - واژه نامه ریاضیات
- فضای هیلبرت - فضای محصول داخلی که از نظر متریک کامل است. یک فضای Banach که هنجار آن باعث تولید داخلی می شود (هنجار هویت متوازی الاضلاع را برآورده می کند)
- چهارمین مشکل هیلبرت
- ایزومتری
- تداوم Lipschitz - شکل قوی تداوم یکنواخت
- اندازه گیری (ریاضیات) - تعمیم طول ، مساحت ، حجم و انتگرال
- متریک (ریاضیات) - فاصله تعریف تابع ریاضی
- نقشه متریک
- امضای متریک
- تانسور متریک
- درخت متریک
- نرمال (ریاضیات) - طول در یک فضای بردار
- فضای بردار نرم شده - فضای بردار که در آن فاصله مشخص می شود
- متریک محصول
- فضا (ریاضیات) - مجموعه ای ریاضی با برخی ساختارهای اضافه شده
- نابرابری مثلث - ویژگی هندسه ، همچنین برای تعمیم مفهوم "فاصله" در فضاهای متریک استفاده می شود
- فضای فرا متریک - نوعی از فضای متریک که در آن نابرابری مثلث با نابرابری قوی تر با استفاده از حداکثر به جای جمع جایگزین می شود







![d '([x]، [y]) = \ inf \ {d (p_1، q_1) + d (p_2، q_2) + \ dotsb + d (p_ {n}، q_ {n}) \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b76c4134b02163411e4c3529bd699762f1e35911)
![[p_1] = [x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d73570f663c6c3b07374f267f5fa4bc1135445)
![[q_n] = [سال]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ced6b87b086042c63417641c63edb4cfc5c3d0a1)




![[0،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) با متریک مقدار مطلق ، تمام فضاهای متریک با امتیازات کاملاً زیاد و
با متریک مقدار مطلق ، تمام فضاهای متریک با امتیازات کاملاً زیاد و  به طوری که هر زیر مجموعه از
به طوری که هر زیر مجموعه از  در برخی از اعضای جلد موجود است.
در برخی از اعضای جلد موجود است. جمع و جور است فضاهای مناسب از نظر محلی جمع و جور هستند ، اما عکس العمل به طور کلی درست نیست.
جمع و جور است فضاهای مناسب از نظر محلی جمع و جور هستند ، اما عکس العمل به طور کلی درست نیست. یک نقشه مداوم وجود دارد
یک نقشه مداوم وجود دارد ![f \ colon [0،1] \ به M](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e6120470fdbecbc919951edc1e54d516e5f461) با
با  و
و  . هر مسیری که به فضای متصل متصل است متصل است ، اما برعکس به طور کلی درست نیست.
. هر مسیری که به فضای متصل متصل است متصل است ، اما برعکس به طور کلی درست نیست. یک فضای متریک غیرخالی است و
یک فضای متریک غیرخالی است و سپس
سپس  یک فضای متریک نوک تیز نامیده می شود ، و
یک فضای متریک نوک تیز نامیده می شود ، و یک نقطه برجسته نامیده می شود . توجه داشته باشید که یک فضای متریک اشاره شده فقط یک فضای متریک غیرخالی است که توجه آن به نقطه متمایز آن جلب شده است و هر فضای متریک غیرخالی را می توان به عنوان یک فضای متریک اشاره شده مشاهده کرد. نقطه متمایز گاهی نشان داده می شود
یک نقطه برجسته نامیده می شود . توجه داشته باشید که یک فضای متریک اشاره شده فقط یک فضای متریک غیرخالی است که توجه آن به نقطه متمایز آن جلب شده است و هر فضای متریک غیرخالی را می توان به عنوان یک فضای متریک اشاره شده مشاهده کرد. نقطه متمایز گاهی نشان داده می شود که در
که در ![{\ displaystyle f ^ {- 1} [U]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c2decf23632b393104f53795355291a1224daa4) در باز است
در باز است  دنباله ای در است
دنباله ای در است  همگرا به
همگرا به که در
که در  و هر
و هر 
 داده شده توسط
داده شده توسط  یک فضای متریک کامل است.
یک فضای متریک کامل است. ، همچنین به
، همچنین به  برای نقاط مشخص
برای نقاط مشخص  . به طور کلی
. به طور کلی می تواند با یک تابع جایگزین شود
می تواند با یک تابع جایگزین شود برای نقاط مشخص
برای نقاط مشخص  با محدود کردن دامنه ، به یک فضای متریک تبدیل می شود
با محدود کردن دامنه ، به یک فضای متریک تبدیل می شود  .
. اگر
اگر و
و در غیر این صورت ، یک مثال ساده اما مهم است و می تواند برای همه مجموعه ها اعمال شود. این ، به ویژه ، نشان می دهد که برای هر مجموعه ، همیشه یک فضای متریک مرتبط با آن وجود دارد. با استفاده از این معیار ، هر نقطه یک
در غیر این صورت ، یک مثال ساده اما مهم است و می تواند برای همه مجموعه ها اعمال شود. این ، به ویژه ، نشان می دهد که برای هر مجموعه ، همیشه یک فضای متریک مرتبط با آن وجود دارد. با استفاده از این معیار ، هر نقطه یک  (یعنی آن دسته از توابع که تصویر یک
(یعنی آن دسته از توابع که تصویر یک  برای هر دو عملکرد محدود شده
برای هر دو عملکرد محدود شده  (جایی که
(جایی که  یک
یک  از رئوس
از رئوس  به طول کوتاهترین مسیر اتصال رئوس
به طول کوتاهترین مسیر اتصال رئوس  و
و  ، به عنوان حداقل تعداد حذف نویسه ، درج یا تعویض مورد نیاز برای تغییر تعریف شده است
، به عنوان حداقل تعداد حذف نویسه ، درج یا تعویض مورد نیاز برای تغییر تعریف شده است ![f \ روده بزرگ [0 ، \ ناکافی] \ rightarrow [0 ، \ ناکارآمد)](https://wikimedia.org/api/rest_v1/media/math/render/svg/a77524e64f5e3e6a98c5efe3d925d54bb8d57e8d) به طوری که
به طوری که اگر و تنها اگر
اگر و تنها اگر  ، سپس
، سپس  همچنین یک معیار در است
همچنین یک معیار در است  به یک فضای متریک
به یک فضای متریک معیاری را در تعریف می کند
معیاری را در تعریف می کند  توسط
توسط  .
. (جایی که
(جایی که  یک عدد واقعی است) در مورد
یک عدد واقعی است) در مورد 
 موجود است در
موجود است در ) در یک فضای متریک
) در یک فضای متریک 
 برای همه
برای همه  . به طور معادل ، می توان از تعریف کلی همگرایی موجود در همه فضاهای توپولوژیک استفاده کرد.
. به طور معادل ، می توان از تعریف کلی همگرایی موجود در همه فضاهای توپولوژیک استفاده کرد. به عنوان هر دو
به عنوان هر دو  با
با .
. ، کامل نیستند
، کامل نیستند
 برای همه
برای همه  صفر است اگر و فقط اگر
صفر است اگر و فقط اگر 
 ، موارد زیر صدق می کند:
، موارد زیر صدق می کند: 


 برای هرچی
برای هرچی 





 - مجموعه ای از زیر مجموعه های
- مجموعه ای از زیر مجموعه های - یک عملکرد
- یک عملکرد - یک
- یک 
 توسط این تعریف می شود:
توسط این تعریف می شود:

 سپس
سپس
 آن را نگه می دارد که
آن را نگه می دارد که
 توابع کاموتونی هستند ، یعنی اگر برای همه باشد
توابع کاموتونی هستند ، یعنی اگر برای همه باشد  آن را نگه می دارد که
آن را نگه می دارد که .
.


 است
است  ادغام پذیر سپس از این فرمول زیر اغلب به عنوان Choquet Integral یاد می شود:
ادغام پذیر سپس از این فرمول زیر اغلب به عنوان Choquet Integral یاد می شود:
 .
. به دست آوردن
به دست آوردن ![\ int_0 ^ 1 G ^ {- 1} (x) dx = E [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ef41e8fdfa3cbf7481bed59bf7f1e2cecdf14fb) ،
،![H (x): = 1 _ {[\ alpha ، x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a8465806e65beea0cc178bbc736895749b382cd) به دست آوردن
به دست آوردن 


 یک تابع فوق اضافی برای اعداد واقعی غیر منفی است زیرا مربع از
یک تابع فوق اضافی برای اعداد واقعی غیر منفی است زیرا مربع از همیشه بزرگتر یا مساوی مربع است
همیشه بزرگتر یا مساوی مربع است  . از این رو
. از این رو
 پس از آن هرمتیان غیر منفی هستند
پس از آن هرمتیان غیر منفی هستند  .
. فوق العاده مثبت است (برابر آن مقعر)
فوق العاده مثبت است (برابر آن مقعر)  .
. ، داشتن یک
، داشتن یک 
 ما داریم:
ما داریم:
 ، درصورتیکه
، درصورتیکه 
 ،
،  وجود دارد و برابر است با
وجود دارد و برابر است با  . (ممکن است حد باشد
. (ممکن است حد باشد .)
.) (بنابراین ممکن است حد بی نهایت مثبت باشد: دنباله را در نظر بگیرید
(بنابراین ممکن است حد بی نهایت مثبت باشد: دنباله را در نظر بگیرید  .)
.) علاوه بر این ، شرط
علاوه بر این ، شرط  ممکن است به شرح زیر ضعیف شود:
ممکن است به شرح زیر ضعیف شود:  به شرطی که
به شرطی که  یک عملکرد در حال افزایش است به طوری که انتگرال
یک عملکرد در حال افزایش است به طوری که انتگرال همگرایی می کند (نزدیک بی نهایت).
همگرایی می کند (نزدیک بی نهایت).  حد
حد  وجود دارد و برابر است با
وجود دارد و برابر است با  (ممکن است حد باشد
(ممکن است حد باشد  )
) . از این رو
. از این رو
![f: [0 ، \ infty] \ به [0 ، \ invyy]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed41bd9bc92db1a1891bae992398448b49b6219) با
با  همچنین فرعی است. برای دیدن این ، ابتدا شخص آن را مشاهده می کند
همچنین فرعی است. برای دیدن این ، ابتدا شخص آن را مشاهده می کند . سپس به جمع این مقید نگاه کنید
. سپس به جمع این مقید نگاه کنید ، سرانجام تأیید می کند که f فرعی است.
، سرانجام تأیید می کند که f فرعی است.  است ، با فرض اینکه میانگین تغییر مقدار نمونه کارها صفر باشد و VaR به عنوان ضرر منفی تعریف شود ،
است ، با فرض اینکه میانگین تغییر مقدار نمونه کارها صفر باشد و VaR به عنوان ضرر منفی تعریف شود ،
 معکوس
معکوس 
 آیا موقعیت های فردی واریانس بازدهی دارند و
آیا موقعیت های فردی واریانس بازدهی دارند و  است
است 
![{\ displaystyle \ rho _ {xy} \ in [-1،1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/353fbcfa41e02d7429827c6c90d393321cb4d9ba) و به طور خاص ، برابر است با مجموع مواجهه فردی با خطر در هنگام
و به طور خاص ، برابر است با مجموع مواجهه فردی با خطر در هنگام  که در صورت عدم تأثیر تنوع در ریسک نمونه کارها است.
که در صورت عدم تأثیر تنوع در ریسک نمونه کارها است. یکی است که اگر
یکی است که اگر  از طول-
از طول- ، بنابراین
، بنابراین  فرعی است و از این رو می توان از لما فاکته برای تخمین رشد استفاده کرد
فرعی است و از این رو می توان از لما فاکته برای تخمین رشد استفاده کرد  مجموعه ای غیر خالی از مجموعه ها باشد. سپس
مجموعه ای غیر خالی از مجموعه ها باشد. سپس اگر
اگر برای همه
برای همه 
 اگر
اگر 
 اگر
اگر  .
. هر زمان که
هر زمان که  . سپس
. سپس یک میدان σ روی مجموعه است
یک میدان σ روی مجموعه است -ring در تقاطع های قابل شمارش بسته شده است. در حقیقت
-ring در تقاطع های قابل شمارش بسته شده است. در حقیقت تابعی باشد که بر روی
تابعی باشد که بر روی  با مقادیر در [−∞ ، + ∞] (به
با مقادیر در [−∞ ، + ∞] (به 

 مجموعه های جدا از هم
مجموعه های جدا از هم  مجموعه های جدا از هم جدا
مجموعه های جدا از هم جدا 
 ⊆
⊆


![A_ {n} = \ چپ [n ، n + 1 \ راست]](https://wikimedia.org/api/rest_v1/media/math/render/svg/de0a0470922097f3463ee9b7056d6b5bb54c391f)
 و
و  فضاهای اندازه پذیر باشند ، به این معنی که
فضاهای اندازه پذیر باشند ، به این معنی که  مجموعه های مجهز به
مجموعه های مجهز به و
و  هستند .یک
هستند .یک  تابع اندازه پذیرگفته می شود اگر برای همه
تابع اندازه پذیرگفته می شود اگر برای همه 

 ، جایی که
، جایی که 


 ، یا سایر فضاهای توپولوژیکی ،
، یا سایر فضاهای توپولوژیکی ،  می
می  یک تابع بورل نیز نامیده می شود . توابع پیوسته توابع بورل هستند اما همه توابع بورل پیوسته نیستند. با این حال ، یک تابع قابل اندازه گیری تقریباً یک تابع پیوستهاست. دیدن
یک تابع بورل نیز نامیده می شود . توابع پیوسته توابع بورل هستند اما همه توابع بورل پیوسته نیستند. با این حال ، یک تابع قابل اندازه گیری تقریباً یک تابع پیوستهاست. دیدن  ، به آن بخش بورل گفته می شود .
، به آن بخش بورل گفته می شود . ، که
، که  هست
هست است
است  . توابع اندازه پذیر لبگ در
. توابع اندازه پذیر لبگ در  ،
،  برای همه
برای همه  اندازه پذیر است . این نیز معادل هر یک از است
اندازه پذیر است . این نیز معادل هر یک از است اندازه پذیر برای همه
اندازه پذیر برای همه  است، پیش نمایش هر مجموعه باز قابل اندازه گیری است. توابع پیوسته ، توابع یکنواخت ، توابع پله ای، توابع نیمه پیوسته ، توابع قابل تلفیق با ریمان و توابع تغییر محدود ، همگی از نظر لبگ اندازه پذیر هستند.
است، پیش نمایش هر مجموعه باز قابل اندازه گیری است. توابع پیوسته ، توابع یکنواخت ، توابع پله ای، توابع نیمه پیوسته ، توابع قابل تلفیق با ریمان و توابع تغییر محدود ، همگی از نظر لبگ اندازه پذیر هستند.  اگر قسمتهای حقیقی و موهومی اندازه پذیر باشند اندازه پذیر است.
اگر قسمتهای حقیقی و موهومی اندازه پذیر باشند اندازه پذیر است. و
و توابعاندازه پذیر هستند ، بنابراین ترکیب آنها نیز چنین است
توابعاندازه پذیر هستند ، بنابراین ترکیب آنها نیز چنین است  .
.  توابع اندازه پذیر ، ترکیب آنها است
توابع اندازه پذیر ، ترکیب آنها است نیازی نیست
نیازی نیست اندازه پذیر است مگر اینکه
اندازه پذیر است مگر اینکه . در واقع ، دو عملکرد اندازه پذیر لبگ ممکن است به گونه ای ساخته شود که ترکیب آنها را غیراندازه پذیر لبگ کند.
. در واقع ، دو عملکرد اندازه پذیر لبگ ممکن است به گونه ای ساخته شود که ترکیب آنها را غیراندازه پذیر لبگ کند. اندازه پذیر است ، که
اندازه پذیر است ، که  ،
،  ، می توان یک
، می توان یک 
 مجهز به
مجهز به  غیرقابل اندازه گیری است
غیرقابل اندازه گیری است  ، از آنجا که پیش نمایش هر نقطه در محدوده زیرمجموعه مناسب و غیر خالی از است
، از آنجا که پیش نمایش هر نقطه در محدوده زیرمجموعه مناسب و غیر خالی از است

 . اجازه دهید
. اجازه دهید زیر مجموعه های Borel از R را نشان می دهد . برای هر
زیر مجموعه های Borel از R را نشان می دهد . برای هر و
و  یک
یک 

 . سپس خانواده زیر مجموعه ها
. سپس خانواده زیر مجموعه ها
 محدود به
محدود به 

 یک
یک  با توجه به جبر بورل در R n قابل اندازه گیری است و سپس
با توجه به جبر بورل در R n قابل اندازه گیری است و سپس 
 با توجه به استوانه σ جبر قابل اندازه گیری است
با توجه به استوانه σ جبر قابل اندازه گیری است  (به بالا مراجعه کنید) برای
(به بالا مراجعه کنید) برای 

 در صورتی که سه ویژگی زیر را برآورده کند ، σ -جبر نامیده می شود :
در صورتی که سه ویژگی زیر را برآورده کند ، σ -جبر نامیده می شود :  برای همه A در جبر بورل در R ،
برای همه A در جبر بورل در R ، یک
یک  مجموعه ای از جبرهای σ بر روی فضای X است .
مجموعه ای از جبرهای σ بر روی فضای X است .


 ، بنابراین
، بنابراین



 یا
یا .
. برای
برای و یک
و یک  بودن
بودن  می تواند تعریف کند
می تواند تعریف کند  ، به اصطلاحσ -جبر τ-گذشته ، که در یک
، به اصطلاحσ -جبر τ-گذشته ، که در یک 
![\ sigma (f) = \ sigma \ چپ (\ {f ^ {- 1} ((a_ {1} ، b_ {1}] \ بار \ cdots \ بار (a_ {n} ، b_ {n}])): a_ {i} ، b_ {i} \ in \ mathbb {R} \} \ سمت راست).](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b610e9556a45c7691834d83cca70a6c7a9d21da)
 و
و  دو فضای قابل اندازه گیری باشد. جبر σ برای
دو فضای قابل اندازه گیری باشد. جبر σ برای  ضرب جبری نامیده می شود و توسط آن تعریف می شود
ضرب جبری نامیده می شود و توسط آن تعریف می شود
 یک سیستم π است
یک سیستم π است![{\ mathcal {B}} (\ mathbb {R} ^ {n}) = \ sigma \ سمت چپ (\ چپ \ {(- \ ضعیف ، b_ {1}] \ بار \ cdots \ زمان (- \ ضعیف ، b_) {n}]: b_ {i} \ in \ mathbb {R} \ right \} \ right) = \ sigma \ چپ (\ چپ \ {(a_ {1} ، b_ {1}] \ بار \ cdots \ بار) (a_ {n} ، b_ {n}]: a_ {i} ، b_ {i} \ in \ mathbb {R} \ right \} \ right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a61219d2f359567ce7b87e8079e1ff2e56f68e8)



 به عنوان مجموعه مشترک وجود دارد.
به عنوان مجموعه مشترک وجود دارد.


 کوچکترین σ -جبر است که شامل تمام موارد دیگر است.
کوچکترین σ -جبر است که شامل تمام موارد دیگر است.

 برای همه
برای همه 
 سپس
سپس 
 . اندازه گیری
. اندازه گیری  و هر مجموعه ای از موارد منفی
و هر مجموعه ای از موارد منفی  تعریف کردن:
تعریف کردن:
 به عنوان برتری کل مبالغ بسیاری از آنها باشد.
به عنوان برتری کل مبالغ بسیاری از آنها باشد. در صورت وجود ، اضافه می شود
در صورت وجود ، اضافه می شود  و هر خانواده ای از مجموعه های جدا از هم
و هر خانواده ای از مجموعه های جدا از هم  وضعیت زیر:
وضعیت زیر:



 .
.

 دارای اندازه گیری محدود است ، پس از آن شرط
دارای اندازه گیری محدود است ، پس از آن شرط

 و
و  دو فضای قابل اندازه گیری هستند ، سپس یک تابع
دو فضای قابل اندازه گیری هستند ، سپس یک تابع از
از  . در این تنظیمات ،
. در این تنظیمات ، 






 یک فضای اندازه گیری باشد. مشخص کن
یک فضای اندازه گیری باشد. مشخص کن
![{\ displaystyle [0 ، + \ infty]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f32245981f739c86ea8f68ce89b1ad6807428d35) . (طبق تعریف ،
. (طبق تعریف ، و تمام زیر مجموعه های بورل از
و تمام زیر مجموعه های بورل از  ) در نظر بگیرید
) در نظر بگیرید عملکرد غیر منفی قابل اندازه گیری
عملکرد غیر منفی قابل اندازه گیری![{\ displaystyle s: \ امگا \ به [0 ، + \ ناکارآمد]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fec4adac6249fed9389e7da9a4a7a5490912a42) . برای یک مجموعه
. برای یک مجموعه ، تعریف کردن
، تعریف کردن
 .
.





 به عنوان یک انتگرال نامناسب وجود دارد و می توان آن را محدوم محاسبه کرد ؛ دو برابر
به عنوان یک انتگرال نامناسب وجود دارد و می توان آن را محدوم محاسبه کرد ؛ دو برابر 



 و
و  متناهی است:
متناهی است:



 است ریمان-انتگرال در نمی
است ریمان-انتگرال در نمی ![\ int _ {[0،1]} 1 _ {\ mathbf {Q}} \ ، d \ mu = \ mu (\ mathbf {Q} \ cap [0،1]) = 0 ،](https://wikimedia.org/api/rest_v1/media/math/render/svg/52bfcea8873ad8a9e5a4b9afdf9615db2e3abbae)

![\ int _ {A} f \، d \ mu = \ int _ {[a، b]} f \، d \ mu](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f93c75ee746be8e05f0e6317fda8db6c41a068)
![\ sum _ {k} \ int f_ {k} (x) dx ، \ quad \ int \ چپ [\ sum _ {k} f_ {k} (x) \ right] dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/f68cd6554ec54e9c92baeba89ac3c7523bae3d64)











 تابع ساده ای است که مقدار آن است
تابع ساده ای است که مقدار آن است  هر زمان که
هر زمان که ، برای k یک عدد صحیح غیر منفی کمتر از (بگویید)
، برای k یک عدد صحیح غیر منفی کمتر از (بگویید) . سپس می توان مستقیماً ثابت کرد که
. سپس می توان مستقیماً ثابت کرد که
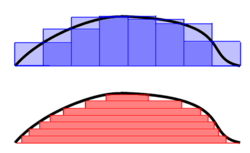

 (در محور x). انتگرال لبگ با برش دادن در امتداد محور y با استفاده از اندازه گیری 1 بعدی Lebesgue برای اندازه گیری "عرض" برش ها بدست می آید.
(در محور x). انتگرال لبگ با برش دادن در امتداد محور y با استفاده از اندازه گیری 1 بعدی Lebesgue برای اندازه گیری "عرض" برش ها بدست می آید.




 تجزیه f به اختلاف دو تابع غیر منفی داده شده توسط است
تجزیه f به اختلاف دو تابع غیر منفی داده شده توسط است



 هنوز هم می توان در مواردی که f و g دارای یک نقطه انقطاع مشترک هستند تعریف شود.
هنوز هم می توان در مواردی که f و g دارای یک نقطه انقطاع مشترک هستند تعریف شود.![{\ displaystyle U (P، f، g) = \ sum _ {i = 1} ^ {n} \، \، [\، g (x_ {i}) - g (x_ {i-1}) \، ] \، \ sup _ {x \ in [x_ {i-1}، x_ {i}]} f (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bcb0bbb9db175769d7860b9d98a9ae1db1a48ac)
![{\ displaystyle L (P، f، g) = \ sum _ {i = 1} ^ {n} \، \، [\، g (x_ {i}) - g (x_ {i-1}) \، ] \، \ inf _ {x \ in [x_ {i-1}، x_ {i}]} f (x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/797c4bd93cc8337923f838ea35a8aef9b35fefe9)

![{\ displaystyle \ lim _ {\ operatorname {mesh} (P) \ تا 0} [\، U (P، f، g) -L (P، f، g) \،] = 0. \ quad}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0fb9c0ebaddaa690918bda4d1a601bfe1d02381)
 که به طور مداوم از هم
که به طور مداوم از هم 
 .
. مورد استفاده در مطالعه
مورد استفاده در مطالعه 


 ، یا برای استفاده
، یا برای استفاده  به عنوان یکپارچه
به عنوان یکپارچه![[a، b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) ، یک "تابع ترجمه"
، یک "تابع ترجمه"  باید تلاقی کند
باید تلاقی کند  دقیقاً یکبار برای هر تغییر در فاصله. سپس یک منطقه "کاوالیر" محدود می شود
دقیقاً یکبار برای هر تغییر در فاصله. سپس یک منطقه "کاوالیر" محدود می شود  ،
،  . پس از آن منطقه منطقه است
. پس از آن منطقه منطقه است جایی که
جایی که  و
و  هستند
هستند  تلاقی کردن
تلاقی کردن 
 از فاصله
از فاصله
![{\ displaystyle S (P، f، g) = \ sum _ {i = 0} ^ {n-1} f (c_ {i}) \ left [g (x_ {i + 1}) - g (x_ { من}) \ راست]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b60856e31ea522340fba3119751286c72478a02d)
 در زیر- i i قرار دارد [ x i ، x i +1 ]. دو عملکرد
در زیر- i i قرار دارد [ x i ، x i +1 ]. دو عملکرد

![{\ displaystyle \ operatorname {E} \ چپ [\ ، \ چپ | f (X) \ راست | \ ، \ راست]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1d4254bc7f459386e9cf4f95c45d7b7822cfe86) متناهی است ، پس تابع چگالی احتمال X مشتق g است و ما داریم
متناهی است ، پس تابع چگالی احتمال X مشتق g است و ما داریم![{\ displaystyle \ operatorname {E} [f (X)] = \ int _ {- \ infty} ^ {\ infty} f (x) g '(x) \، \ mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02c918164beb4c73f48bfc4db0251c4891d81d70)
![{\ displaystyle \ operatorname {E} [f (X)] = \ int _ {- \ infty} ^ {\ infty} f (x) \، \ mathrm {d} g (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c52b0802dcb12f1a5957542fc5d00c8719d22aac)
![{\ displaystyle \ operatorname {E} \ left [X ^ {n} \ right] = \ int _ {- \ infty} ^ {\ infty} x ^ {n} \، \ mathrm {d} g (x). }](https://wikimedia.org/api/rest_v1/media/math/render/svg/55747a21ca454ad3df714b484adc20921de0f2d5)


 .
.
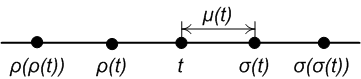
 ، به ترتیب. به طور رسمی:
، به ترتیب. به طور رسمی: (اپراتور شیفت جلو / اپراتور جهش رو به جلو)
(اپراتور شیفت جلو / اپراتور جهش رو به جلو) (اپراتور تغییر عقب / عملگر پرش به عقب)
(اپراتور تغییر عقب / عملگر پرش به عقب)
 و
و  .
.
 ،
، 


 است متراکم
است متراکم است متراکم چپ و راست پراکنده
است متراکم چپ و راست پراکنده است جدا شده
است جدا شده است به سمت چپ پراکنده و متراکم راست
است به سمت چپ پراکنده و متراکم راست ،
، وجود دارد اگر و فقط اگر:
وجود دارد اگر و فقط اگر: یک محله وجود دارد
یک محله وجود دارد 
 که در
که در  سپس
سپس  ؛ مشتق مورد استفاده در
؛ مشتق مورد استفاده در  (
(  ،
، 

 یک مشتق مداوم دارد
یک مشتق مداوم دارد  یکی تنظیم می شود
یکی تنظیم می شود
![{\ mathcal {Z}} '\ {x [z] \} = {\ frac {{\ mathcal {Z}} \ {x [z + 1] \}} {z + 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0eff16581e442c4142fd193357778ff342911e5)

 نشانگر
نشانگر  عملگر تغییر عقب است که در مشخص شده است
عملگر تغییر عقب است که در مشخص شده است 




![f (t) = \ sin (t) ، \ quad t \ in [- \ pi ، \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f5a62642ad4f66510bdde0918bab7caf79c64e6) و {\ displaystyle f (t) = 0}
و {\ displaystyle f (t) = 0} در غیر این صورت.
در غیر این صورت.![f (t) = {\ frac {1} {t}} ، \ quad t \ in [0،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aeff78fa14fae46a25060d2a74afc98bae569d9) و
و  .
. سیگنال در بی نهایت قابل جمع نیست ، اما
سیگنال در بی نهایت قابل جمع نیست ، اما  است).
است).
 و
و  ، سپس برای t = 1 داریم
، سپس برای t = 1 داریم ، و برای t = 2 داریم
، و برای t = 2 داریم .
.

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.