مدلسازی و ابزارهای تجربی با پروفسور مگنس
روش های محاسباتی در مکانیک کوانتومی
در این پست سعی خواهم کرد دو روش محاسباتی را که معمولا برای تجزیه و تحلیل سیستم های کوانتومی استفاده می شود به خواننده آموزش دهم. این روش ها به روش تطبیق و روش مونت کارلو معروف هستند. این روش ها هر کدام مزایا و معایب خاص خود را در سناریوهای مختلف دارند، به همین دلیل است که معتقدم برای خواننده مفید است که هر دوی این روش ها را در کمربند ابزار خود داشته باشند.
اساس همه محاسبات ما در یک سیستم کوانتومی معمولاً بر اساس معادله شرودینگر مستقل از زمان است، بنابراین اجازه دهید ابتدا این معادله را تجزیه و تحلیل کنیم تا ببینیم چگونه می توان از آن در محاسبات استفاده کرد.
ما می توانیم مشتق جزئی دو تابع موج را به صورت تقریبی تقریبی کنیم:
اکنون که معادله ای برای مشتق جزئی دوگانه داریم، می توانیم آن را دوباره وارد معادله شرودینگر کرده و عبارت ها را به صورت زیر مرتب کنیم:
اکنون معادله ای داریم که به ما امکان می دهد هر تابع موجی را با توجه به انرژی و پتانسیل محاسبه کنیم.
روش تطبیق
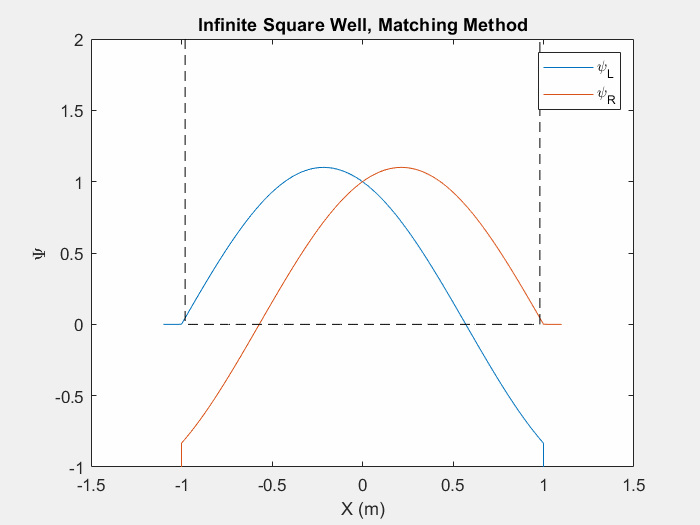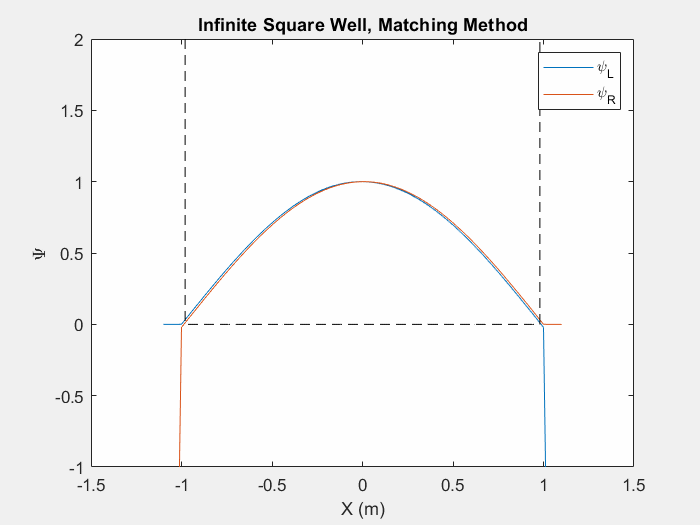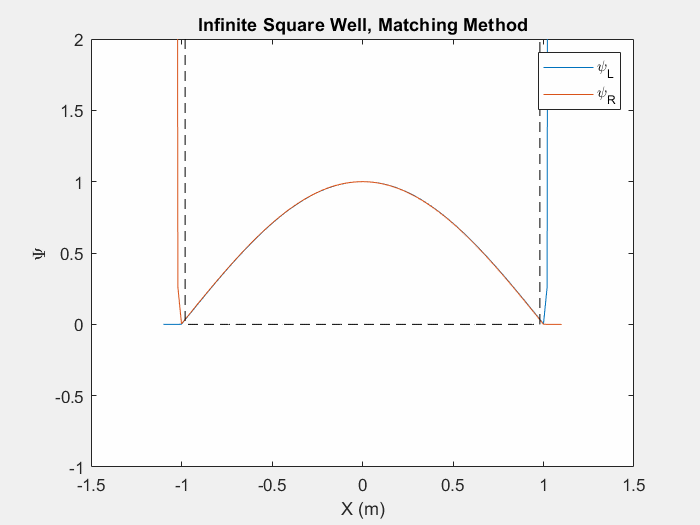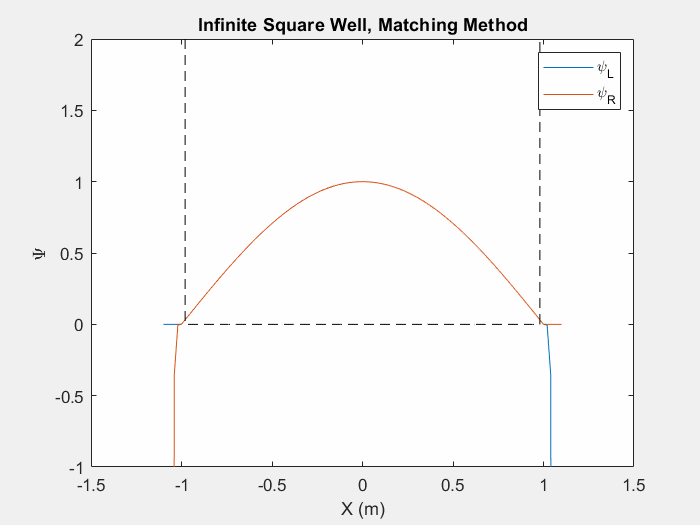
اکنون که میتوانیم یک تابع موج را محاسبه کنیم، باید انرژیهای ویژه مرتبط با یک سیستم را پیدا کنیم تا حالت ویژه را تعیین کنیم. راه های متعددی برای انجام این کار وجود دارد، یکی از آن ها روش تطبیق است که به ویژه برای سیستم های پتانسیل نامتقارن مفید است. هدف تابع تطبیق ایجاد یک تابع موج صاف و پیوسته با ترکیب دو تابع موج است که از گوشه های چپ و راست آرایه پتانسیل تولید می شوند.
شکل (1) - روش تطبیق در داخل یک چاه مربع بی نهایت.
ورودی های تابع روش تطبیق عبارتند از حدس اولیه انرژی، آرایه پتانسیل، اندازه گام فضایی و یک نقطه نمایه سازی که برای بررسی شیب هر تابع موج از آن استفاده خواهیم کرد. برای محاسبه هر تابع موج، شرایط اولیه منحصر به فرد برای جواب های برابری زوج و فرد وجود دارد:
با استفاده از معادله 3 و شرایط اولیه، می توانیم تابع موج اول را با استفاده از حدس انرژی اولیه خود محاسبه کنیم. سپس، این فرآیند را با برگرداندن آرایه پتانسیل و ایجاد تابع موج دوم با همان شرایط اولیه تکرار می کنیم. سپس این تابع موج دوم را برمیگردانیم تا به طور موثر یک آرایه از چپ به راست و یک آرایه دوم از راست به چپ ایجاد کنیم. سپس هر تابع موج را در نقطه نمایه شده نرمال می کنیم تا آنها را قطع کنند.
اکنون ممکن است شیب هر تابع موج را در شاخص محاسبه کنیم. سپس یک تابع تطبیق ثانویه را فراخوانی می کنیم که جهت شیب ها را پیگیری می کند. اگر جهت گیری نسبی هر شیب ثابت باقی بماند، آنگاه مقدار «تغییر در انرژی» ما، که در ادامه اضافه خواهیم کرد، ثابت می ماند. اگر جهت گیری نسبی هر شیب تغییر کند، آنگاه مقدار «تغییر انرژی» ما نصف و نفی می شود. در هر صورت، مقدار «تغییر در انرژی» را به حدس اولیه انرژی اضافه میکنیم، توابع موج چپ و راست را دوباره محاسبه میکنیم و فرآیند را تکرار میکنیم.
این تابع به ما امکان می دهد حالت های ویژه را پیدا کنیم و انرژی های ویژه یک سیستم را بررسی کنیم. زمانی که به حد معینی رسیدیم، مقدار «تغییر انرژی» آنقدر کم خواهد بود که میتوانیم برنامه را متوقف کرده و دو تابع را در نقطه شاخص ادغام کنیم.
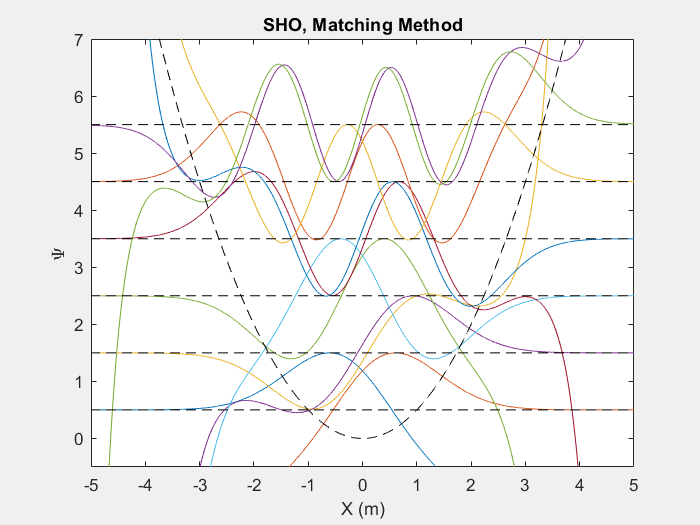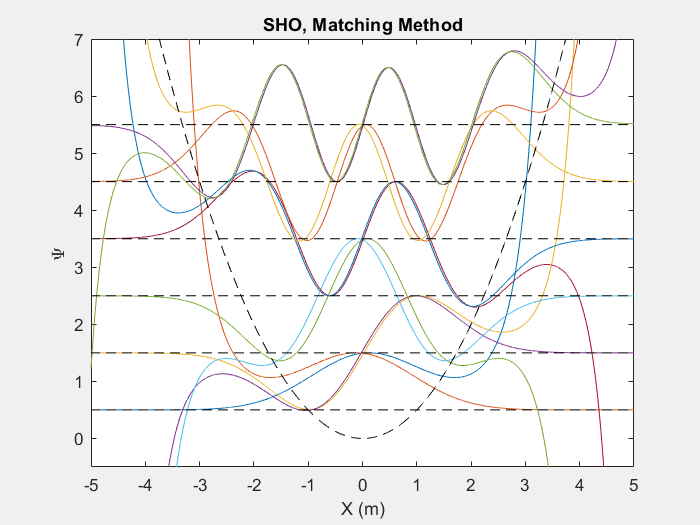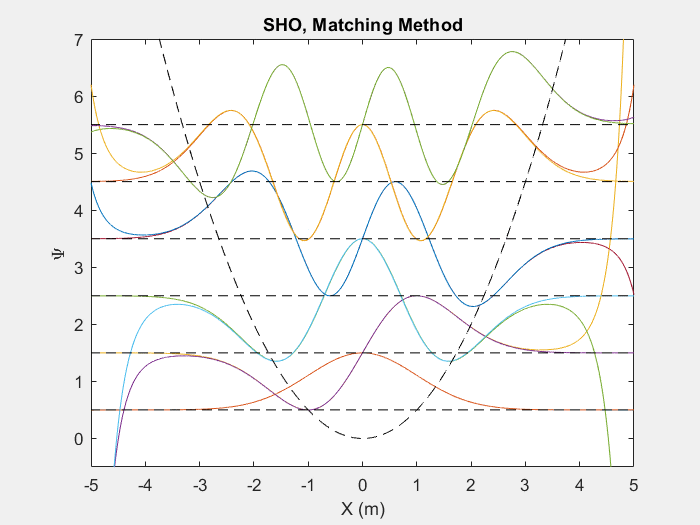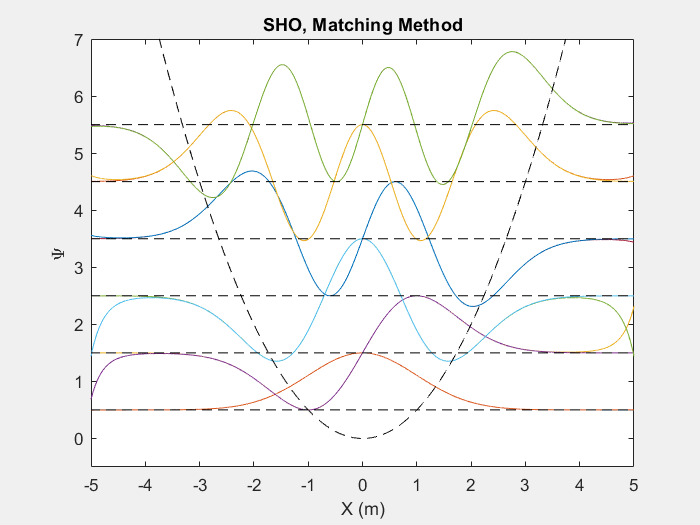
کاربردهای بسیار مفیدی از این روش وجود دارد که یکی از آنها نوسان ساز هارمونیک کوانتومی است. نوسان ساز هارمونیک کوانتومی یک آنالوگ مفید برای بسیاری از پتانسیل های دلخواه است که دارای نقاط تعادل پایدار هستند.
شکل (2) - بالا روش تطبیقی را نشان می دهد که روی 6 سطح انرژی اول یک نوسان ساز هارمونیک کوانتومی اجرا می شود. پایین نتیجه نهایی را نشان می دهد.
شکل (3) - توزیع احتمال 100 سطح انرژی در نتیجه روش تطبیق.
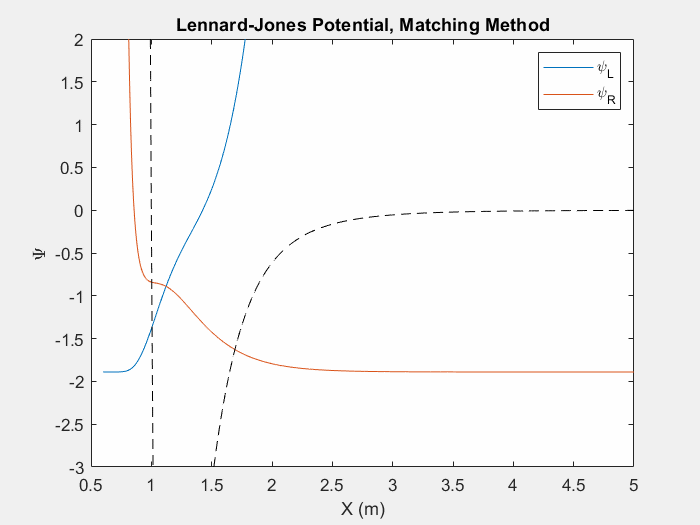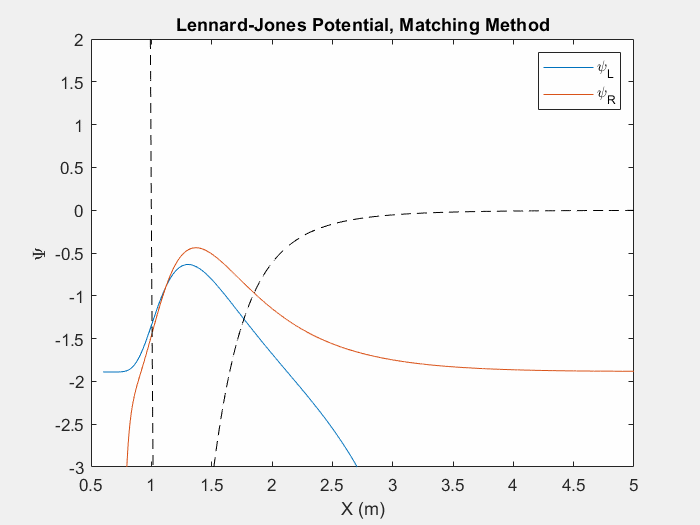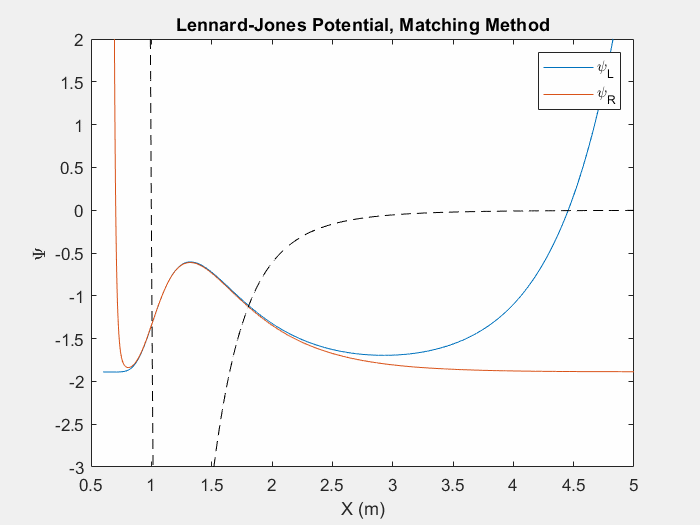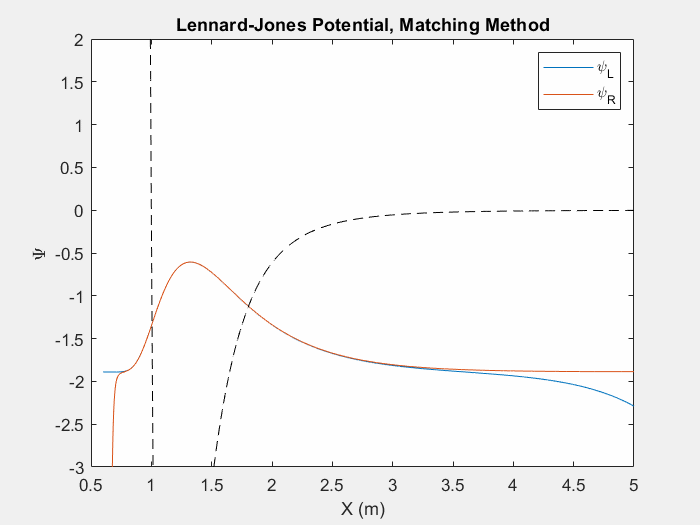
شکل (4) - یکی دیگر از پتانسیل های مفید برای مطالعه، پتانسیل لنارد جونز است. این پتانسیل برای مدل سازی نیروهای واندروالس بین اتم های بی اثر استفاده می شود.
روش مونت کارلو
یکی دیگر از روش های محاسباتی مفید، روش مونت کارلو است. به جای حدس زدن انرژی مانند روش تطبیق، در این روش تابع موج را حدس زده و بر اساس این حدس تکرار میکنیم. ایده روش مونت کارلو این است که ما به طور تصادفی یک سیستم را تغییر می دهیم و فقط تغییراتی را حفظ می کنیم که ما را به راه حلی که انتظارش را داریم نزدیکتر می کند. در مورد مکانیک کوانتومی، این برای تغییر تصادفی تابع موج و حفظ تغییراتی که انرژی سیستم را کاهش می دهد، استفاده می شود.
برای اجرای این رویکرد، ابتدا باید نحوه محاسبه انرژی را با استفاده از رابطه 4 زیر درک کنیم:
برای پیشفرم کردن این انتگرالها در فضای گسسته، میتوانیم از چندین روش مختلف استفاده کنیم، اما برای این فرآیند من از روش انتگرال ذوزنقهای استفاده کردم:
با اعمال این روش بر ضریب و مخرج معادله 4، معادلات زیر به دست می آید:
حال معادله 4 می شود:
اما اکنون در هر دو طرف معادله انرژی داریم. برای حل این مشکل، باید معادله شرودینگر مستقل از زمان (معادله 1) را جایگزین کنیم.
در نهایت برای خلاص شدن از مشتقات جزئی دوگانه، معادله 2 را جایگزین می کنیم و پیدا می کنیم:
این راه حل نهایی است که به ما امکان می دهد انرژی را در هر سیستمی با تابع موج و آرایه پتانسیل محاسبه کنیم.
اکنون که می توانیم انرژی را محاسبه کنیم، می توانیم از روش مونت کارلو استفاده کنیم. این روش در واقع بسیار ساده است. تابعی ایجاد می کنیم که تابع موج را به صورت دلخواه حدس می زند و انرژی این حدس را محاسبه می کند. سپس به طور تصادفی نقطه ای از تابع موج را انتخاب می کنیم و آن را به مقدار تصادفی تغییر می دهیم. سپس انرژی سیستم را دوباره محاسبه می کنیم و اگر انرژی کاهش یافته است، می توانیم آن تغییر تصادفی را حفظ کنیم، در غیر این صورت تغییر را کنار گذاشته و به تابع موج قبلی بر می گردیم. این فرآیند را بارها و بارها تکرار می کنیم تا به نقطه ای برسیم که پس از تعداد مشخصی تلاش، انرژی تغییر نکند. در این مرحله می توانیم فرض کنیم که به وضعیت پایه سیستم بالقوه خود رسیده ایم.
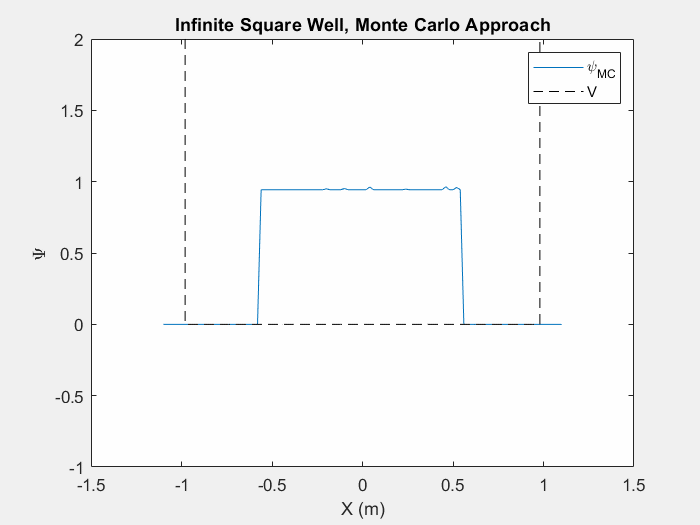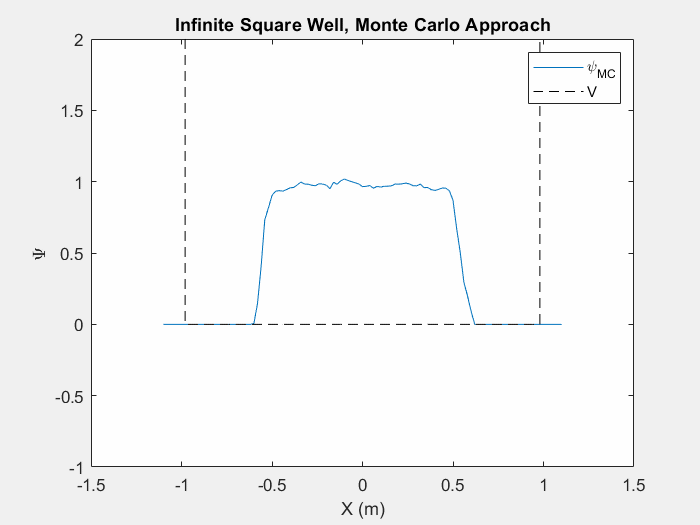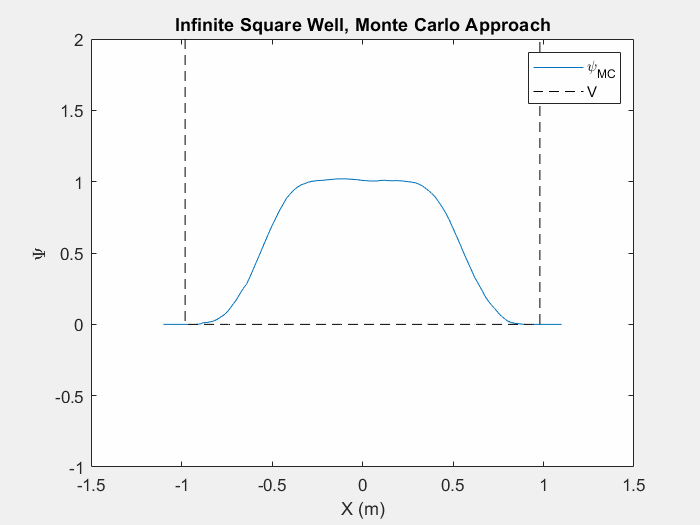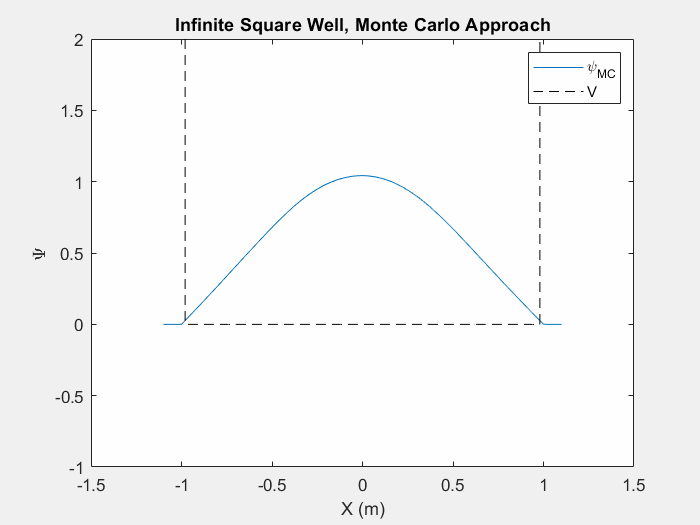
شکل (5) - روش مونت کارلو در چاه مربع بی نهایت. این انیمیشن بیش از 5 میلیون بار تکرار می شود.
شکل (6) - روش مونت کارلو در پتانسیل لنارد جونز. این انیمیشن بیش از 50 میلیون بار تکرار می شود.
معمولاً هنگام استفاده از روش مونت کارلو در یک سیستم پتانسیل جدید، تشخیص اینکه چه زمانی به حالت پایه رسیدهایم بسیار دشوار است، مگر اینکه واقعاً تکرارها را هنگام وقوع تماشا کنیم. همانطور که تابع موج شروع به تغییر کمتر و کمتر می کند، می توانیم فرض کنیم که به حالت پایه نزدیک می شویم. این هنوز یک فرآیند بسیار کند است و بسته به حدس اولیه تابع موج و اندازه گام تغییرات تصادفی شما، ممکن است زمانهای بسیار متفاوتی طول بکشد تا به حالت پایه برسد.
در حالی که روش مونت کارلو به طور قابل توجهی کندتر از روش تطبیق است، اما همچنان در یافتن انرژی حالت پایه یک سیستم دلخواه بسیار مفید است. ما معمولاً به شهود کمی نیاز داریم که هنگام حدس زدن تابع موج اولیه، حالت پایه چگونه به نظر می رسد. تا زمانی که روش مونت کارلو برای مدت زمان کافی اجرا شود، تابع به حالت پایه نزدیک می شود. یکی دیگر از نکات منفی روش مونت کارلو این است که فقط حالت پایه را جستجو می کند. با این حال، روش تطبیق در یافتن سطوح انرژی چندگانه مفید است. این روش در اطراف هر حالت ویژه طنین انداز خواهد شد تا زمانی که حدس انرژی اولیه و مقدار "تغییر انرژی" ما اجازه دهد. به طور کلی، هر دو عملکرد کاربردهای خود را دارند و می توانند در کنار هم بسیار مفید باشند.
به عنوان یک کنار، همچنین باید بگویم که هر دوی این روشها تنها زمانی مفید هستند که ما قبلاً نحوه توصیف پتانسیل یک سیستم را درک کرده باشیم و فقط به دنبال انرژیهای ویژه سیستم مذکور باشیم. در دنیای واقعی، اکثر محققان معمولاً از مشکل معکوس رنج می برند، که در آن ما انرژی های سیستم را می شناسیم اما باید از این اطلاعات برای ساختن پتانسیلی که با این انرژی ها منطبق است استفاده کنیم. اگرچه این روشها ممکن است برای آن محققان مفید نباشند، من هنوز فکر میکنم این روشها ارزشمند هستند، بهویژه برای دانشآموزانی که میخواهند سیستمهایی را مطالعه کنند که ممکن است از قبل بدانیم چگونه توصیف کنیم.
https://pages.vassar.edu/magnes/2019/05/10/computational-methods-in-quantum-mechanics/
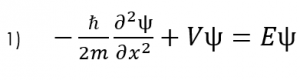
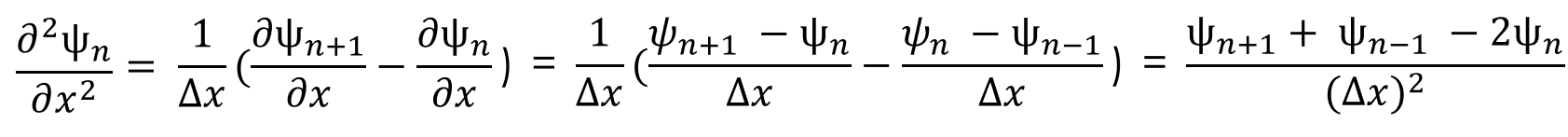
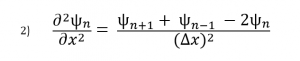
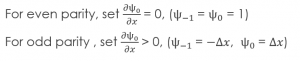


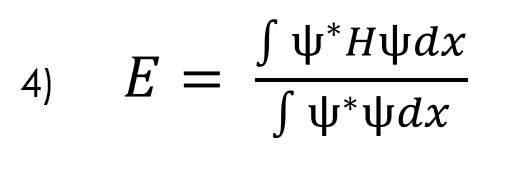
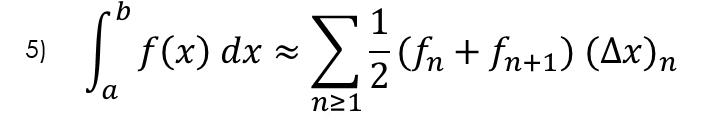


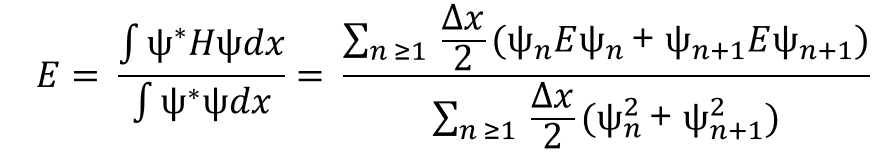



 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.