هنگام انجام ضرب یا یافتن توان یا ریشه اعداد مختلط می توان از فرم اویلر نیز استفاده کرد.

شکل اویلر از عدد مختلط

اتحاد زیر به فرمول اویلر معروف است

e ^i θ = cos θ + i sin θ  

فرمول اویلر شکل قطبی z = re ^i θ را می دهد

توجه داشته باشید

هنگام انجام ضرب یا یافتن توان یا ریشه اعداد مختلط می توان از فرم اویلر نیز استفاده کرد.

مثال 2.22

مدول و آرگومان اصلی اعداد مختلط زیر را بیابید.

(i) √3 + i 

(ii) -√3 + i 

(iii) - √3 - i 

(IV) √3 - i

راه حل

(i) √3 + i

مدول =

از آنجایی که عدد مختلط دارای مقدار اصلی

√3 + i

 در ربع اول است، دارای ارزش اصلی است.

 θ = α = π/6.

بنابراین، مدول و آرگومان اصلی

√3 + i 

به ترتیب 2 و π/6 هستند.

(ii) -√3 + i

مدول = 2 و

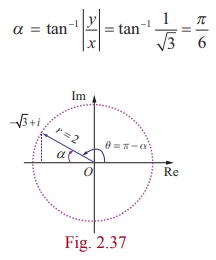
از آنجایی که عدد مختلط

-√3 + i 

در ربع دوم قرار دارد دارای ارزش اصلی است

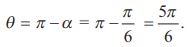
بنابراین مدول و آرگومان اصلی

(ii) -√3 + i

 به ترتیب 2 و 5π/6 هستند.

(iii) - √3 - i

r = 2 و α = π / 6 .

از آنجایی که عدد مختلط

- √3 - i

 در ربع سوم قرار دارد، دارای ارزش اصلی است،

بنابراین، مدول و آرگومان اصلی

- √3 - i

 به ترتیب 2 و -5π/6 هستند.

(IV) √3 - i

r = 2 و α = π/6

از آنجایی که عدد مختلط در ربع چهارم قرار دارد، دارای ارزش اصلی است،

θ = -α = -π/6

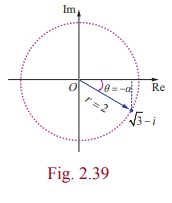
بنابراین، مدول و استدلال اصلی از

√3 - i   2

و

- π/6

هستند.

در هر چهار حالت، مدول مساوی است، اما آرگومان ها به ربعی که عدد مختلط در آن قرار دارد بستگی دارد.

مثال 2.23

عدد مختلط

 -1- i 

1+ i √3

را به شکل قطبی نشان دهید.

راه حل

 (i) فرض کنید

-1- i = r (cosθ + i sinθ )

ما داریم 

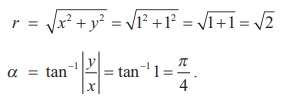
از آنجایی که عدد مختلط -1- i در ربع سوم قرار دارد، دارای ارزش اصلی است،

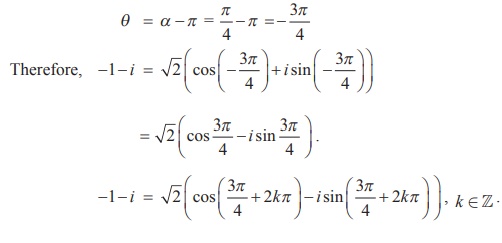
توجه داشته باشید

بسته به مقادیر مختلف k ، اشکال قطبی جایگزین مختلفی را دریافت می کنیم.

(ii) 1+ i√3

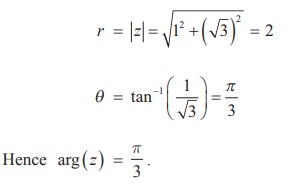
بنابراین، شکل قطبی 1+ i√3 را می توان به صورت نوشتاری نوشت

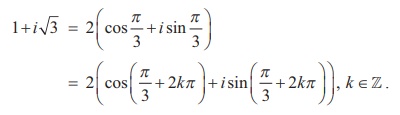
مثال 2.24

آرگومان اصلی Arg z را پیدا کنید، وقتی z = -2 / [ 1+ i √3 ]. 

راه حل

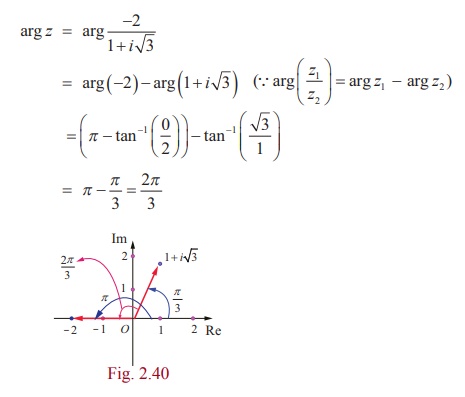
این بدان معناست که یکی از مقادیر arg z 2π/3 است.

از آنجایی که 2π/3 بین -π و π قرار دارد، آرگومان اصلی Arg z 2 π/3 است.

خواص فرم قطبی

فرمول1

اگر z = r (cos θ + i sin θ )، آنگاه z^ -1 =1/ r   (cos θ - i sin θ ) .

اثبات

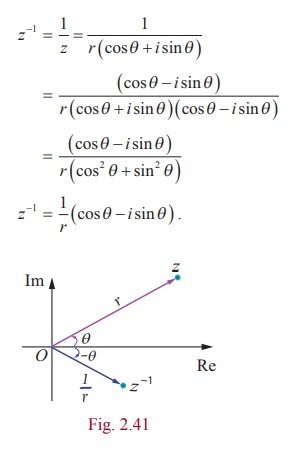
فرمول2

اگر z 1   = r 1 (cos θ 1   + i sin θ 1 ) و  z 2   = r 2 (cos θ 2   + i sin θ 2 ) ،

سپس   z 1 z 2   = r 1 r 2 (cos ( θ 1   + θ 2 ) + i sin ( θ 1   + θ 2 )) .

اثبات

z = r (cos θ 1 + i sin θ 1 ) و  

z  = r (cos θ 2 + i sin θ 2 ) 

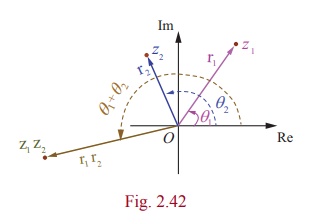
⇒ z 1 z 2   =  r 1 (cos θ 1   + i sin θ 1 ) r 2 (cos θ 2   + i sin θ 2 )

=  r 1 r 2 ((cos θ 1 cos θ 2   - sin θ 1 sin θ 2 ) + i ( sin θ 1 cos θ 2   + sin θ 2   cos θ 1 ))

z 1 z 2   =  r 1 r 2 (cos ( θ 1   + θ 2 ) + i sin ( θ 1   + θ 2 )) .

توجه داشته باشید

 arg ( z 1 z 2 ) = θ 1 + θ 2 = arg ( z 1 ) + arg ( z 2 ) .

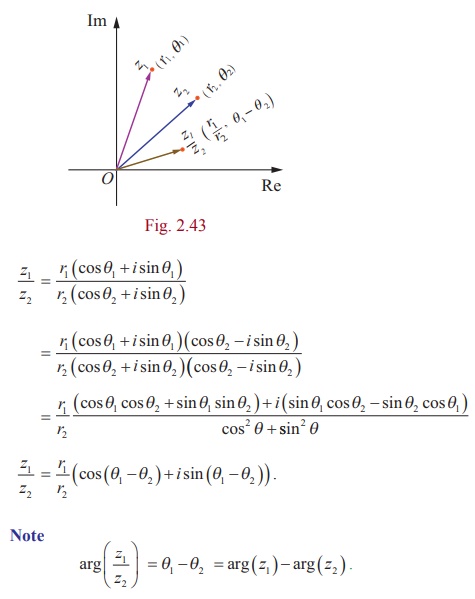
فرمول3

اثبات

با استفاده از شکل قطبی z 1 و z 2 ، داریم 

مثال 2.25

ضرب را 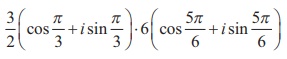  به شکل مستطیل پیدا کنید. 

راه حل

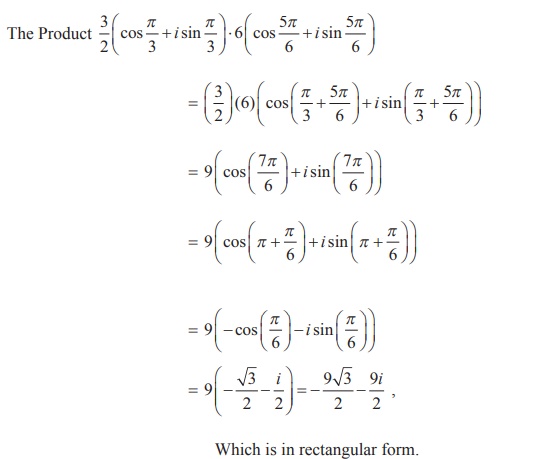
مثال 2.26

ضریب را 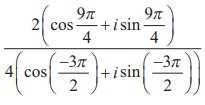  به شکل مستطیل پیدا کنید. 

راه حل

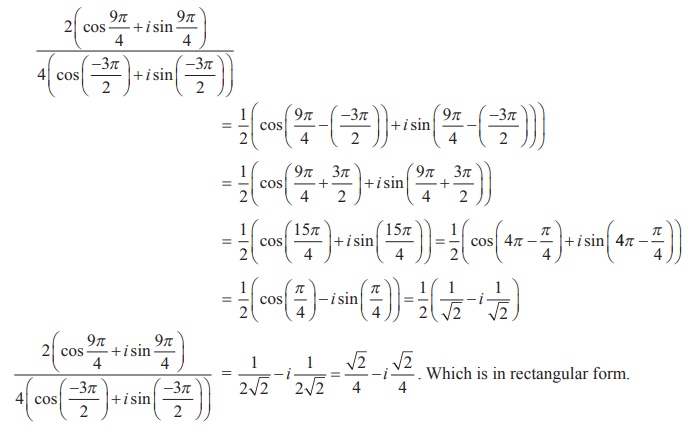
که به شکل مستطیل است.

مثال 2.27

اگر z = x + iy و 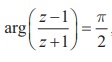 ، نشان دهید که x^ 2 + y ^2 = 1. 

راه حل

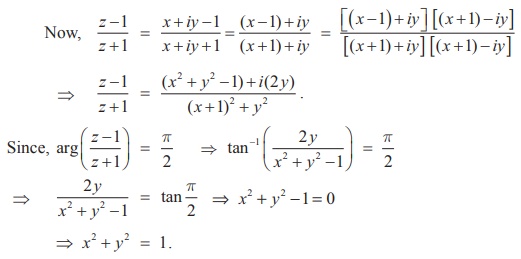
⇒ x^ 2 + y^ 2 =1

منبع

https://www.brainkart.com/article/Euler---s-Form-of-the-complex-number_39103/