ثابت ساز
قضیه ثابت ساز مدار و لم برونساید [ ویرایش ]
مدارها و ثابت ساز ها ارتباط نزدیکی با هم دارند. برای x ثابت در X ، نقشه را در نظر بگیرید



به عبارت دیگر، 







اگر G متناهی باشد، قضیه ثابت ساز مدار، همراه با قضیه لاگرانژ ، به دست می دهد.
به عبارت دیگر طول مدار x برابر ترتیب ثابت ساز آن، ترتیب گروه است. به طور خاص این امر به این معنی است که طول مدار مقسوم علیهای از ترتیب گروه است.
مثال: فرض کنید G گروهی از مرتبه اول p باشد که روی یک مجموعه X با k عنصر عمل می کند. از آنجایی که هر مدار دارای 1 یا p عنصر است، حداقل وجود دارد
این نتیجه به ویژه مفید است زیرا می توان آن را برای شمارش آرگومان ها به کار برد (معمولاً در موقعیت هایی که X نیز محدود است).
نمودار مکعبی با رئوس برچسب گذاری شده
مثال: میتوانیم از قضیه ثابتکننده مدار برای شمارش خودمورفیسمهای یک گراف استفاده کنیم . نمودار مکعبی را مانند تصویر در نظر بگیرید و اجازه دهید G گروه خودمورفیسم آن را نشان دهد . سپس G بر روی مجموعه رئوس {1، 2، ...، 8} عمل میکند، و این عمل گذرا است، همانطور که با ایجاد چرخش در مرکز مکعب مشاهده میشود. بنابراین، با قضیه مدار ثابت ساز،







نتیجه ای که نزدیک به قضیه ثابت ساز مدار است ، لم برونساید است :
که در آن X g مجموعه نقاط ثابت شده توسط g است . این نتیجه عمدتاً زمانی کاربرد دارد که G و X محدود هستند، زمانی که می توان آن را به صورت زیر تفسیر کرد: تعداد مدارها برابر است با میانگین تعداد نقاط ثابت در هر عنصر گروه.
رفع یک گروه G ، مجموعه ای از تفاوت های رسمی محدود G -sets یک حلقه به نام به شکل حلقه های برونساید از G ، که در آن مربوط به مجزای ، ضرب و به ضرب دکارتی .
مثالها [ ویرایش ]
- در عمل بی اهمیت هر گروهGدر هر مجموعهXبا g ⋅ x = x برای همهgدرGو همهxدرX تعریف می شود. یعنی هر عنصر گروهیجایگشت هویت رادرXالقا میکند. [9]
- در هر گروه G ، ضرب چپ یک عمل است G در G : G ⋅ X = GX برای همه گرم ، X در G . این عمل آزاد و متعدی (منظم) است و مبنای اثبات سریع قضیه کیلی را تشکیل می دهد - که هر گروه نسبت به زیر گروهی از گروه متقارن جایگشت های مجموعه G هم شکل است .
- در هر گروه G با زیرگروه H ، ضرب چپ یک عمل است G در مجموعه ای از هممجموعهs G / H : گرم ⋅ ق = گاه برای همه گرم ، در G . به ویژه اگر H حاوی هیچ زیر گروه نرمال حجم قابل توجهی از G این القا ریخت از G به یک زیر گروه از گروه جایگشت از درجه [G: H] .
- در هر گروه G ، صرف یک عمل است G در G : G ⋅ X = gxg -1 . نماد نمایی معمولاً برای نوع عمل راست استفاده می شود: x g = g -1 xg ; ( x g ) h = x gh را برآورده می کند .
- در هر گروه G با زیرگروه H ، صرف یک عمل است G در ترکیبات از H : گرم ⋅ K = GKG -1 برای همه گرم در G و K ترکیبات از H .
- گروه متقارن S n و زیرگروه های آن بر روی مجموعه { 1, …, n } با تغییر عناصر آن عمل می کنند.
- گروه تقارن از یک جسم چند وجهی بر روی مجموعه ای از رئوس که چند وجهی عمل می کند. همچنین روی مجموعه صورت ها یا مجموعه لبه های چند وجهی عمل می کند.
- گروه تقارن هر جسم هندسی روی مجموعه نقاط آن جسم عمل می کند.
- گروه اتومورفیسم یک فضای برداری (یا نمودار ، یا گروه، یا حلقه...) بر روی فضای برداری (یا مجموعه رئوس نمودار، یا گروه، یا حلقه...) عمل می کند.
- گروه خطی عمومی GL( n ، K ) و زیر گروه های آن، به ویژه زیر گروه های Lie آن (شامل گروه خطی ویژه SL( n ، K ) ، گروه متعامد O( n ، K ) ، گروه متعامد خاص SO( n ، K ) ، و گروه ها symplectic SP ( N ، K ) ) هستند گروه های دروغ که عمل در بردار K N. عملیات گروه توسط ضرب ماتریس از گروه با بردار از داده K N .
- گروه خطی عمومی GL( n , Z ) روی Z n با عمل ماتریس طبیعی عمل می کند. مدارهای عمل آن توسط بزرگترین مقسوم علیه مشترک مختصات بردار در Z n طبقه بندی می شوند .
- گروه آفین به عمل انتقالی در نقاط از یک فضای آفین به ، و زیرگروه V از گروه آفین به (این است که، یک فضای برداری) است متعدی و رایگان (این است که، به طور منظم ) اقدام در این نقاط؛ [10] در واقع می توان از این برای ارائه تعریفی از یک فضای وابسته استفاده کرد .
- تصویری خطی گروه PGL ( N + 1، K ) و زیر گروه خود، به خصوص زیر گروه دروغ آن است، که گروه های دروغ که عمل در فضای تصویری P N ( K ). این ضریب عمل گروه خطی کلی در فضای تصویری است. به ویژه قابل توجه PGL(2، K ) است ، تقارن های خط پرتابی، که به شدت 3-گذر است، و نسبت متقاطع را حفظ می کند . گروه موبیوس PGL (2، C ) بسیار جالب توجه است.
- ایزومتری از عمل فضا بر روی مجموعه ای از تصاویر 2D و الگوها، مانند الگوهای تصویر زمینه . تعریف را می توان با مشخص کردن اینکه منظور از تصویر یا الگو، به عنوان مثال، تابعی از موقعیت با مقادیر در مجموعه ای از رنگ ها، دقیق تر می شود. ایزومتریک ها در واقع نمونه ای از گروه افین (عمل) هستند. [ مشکوک - بحث ]
- مجموعه هایی که توسط یک گروه G بر روی آنها اعمال می شود شامل دسته مجموعه های G است که در آنها اشیاء مجموعه های G هستند و مورفیسم ها هممورفیسم های مجموعه G هستند : توابع f : X → Y به گونه ای که g ⋅( f ( x )) = f ( گرم ⋅ X ) برای هر گرم در G .
- گروه گالوا از یک فرمت درست L / K در زمین L عمل می کند اما تنها یک عمل پیش پا افتاده در عناصر از رشته K. گروه های زیر گال (L / K) مربوط به رشته های فرعی L که حاوی K، این است که، زمینه میانی پسوند بین L و K.
- گروه افزایشی اعداد حقیقی ( R , +) بر روی فضای فاز سیستم های " خوب رفتار " در مکانیک کلاسیک (و در سیستم های دینامیکی کلی تر ) با ترجمه زمانی عمل می کند : اگر t در R باشد و x در فاز باشد. فضا، سپس x وضعیتی از سیستم را توصیف می کند، و t + x به عنوان وضعیت سیستم t ثانیه بعد اگر t مثبت باشد یا - t ثانیه قبل اگر t منفی است، تعریف می شود.
- گروه افزودنی از اعداد حقیقی ( R ، +) در مجموعه ای از توابع حقیقی یک متغیر واقعی در شیوه های مختلف عمل می کند، با ( تی ⋅ F ) ( X ) برابر، برای مثال، F ( X + تی ) ، F ( x ) + t , f ( xe t ) , f ( x ) e t , f ( x + t ) e t , یا f ( xe t) + t , اما نه f ( xe t + t ) .
- با توجه به اقدام گروهی از G در X ، ما می توانیم یک عمل ناشی از تعریف G در مجموعه قدرت از X ، با تنظیم گرم ⋅ U = { گرم ⋅ تو : تو ∈ U } برای هر زیر مجموعه U از X و هر گرم در G . برای مثال، در مطالعه عملکرد گروه بزرگ ماتیو در یک مجموعه 24 و در مطالعه تقارن در مدلهای خاصی از هندسههای محدود مفید است .
- چهارگان با هنجار 1 ( versors )، به عنوان یک گروه ضربی، عمل می کنند در R 3 : برای هر چهارگانه مانند Z = COS α / 2 + V گناه α / 2 ، نقشه برداری F ( X ) = Z X Z * است چرخش در جهت خلاف جهت عقربه های ساعت از طریق زاویه α حول محوری که توسط بردار واحد v . z همان چرخش است. کواترنیون ها و چرخش فضایی را ببینید. توجه داشته باشید که این یک عمل وفادار نیست زیرا کواترنیون −1 تمام نقاطی را که در آن قرار داشتند، ترک میکند، همانطور که کواترنیون 1 نیز انجام میدهد.
- با توجه به چپ G -sets
، یک مجموعه G سمت چپ وجود دارد
که عناصر آن نقشه های معادل G هستند
، و با G- action سمت چپ داده شده توسط
(جایی که "
" نشان دهنده ضرب درست در است {\displaystyle g}
). این مجموعه G این ویژگی را دارد که نقاط ثابت آن با نقشه های معادل مطابقت دارند
; به طور کلی، یک شی نمایی در دسته مجموعه های G است .
اقدامات گروهی و گروپوئیدها [ ویرایش ]
مفهوم کنش گروهی را می توان با استفاده از اکشن گروپوئید در زمینه وسیع تری قرار داد 
این گروه اکشن دارای یک مورفیسم p است : G' → G که مورفیسم پوششی گروهوئیدها است . این اجازه می دهد تا یک رابطه بین چنین مورفیسم ها و نقشه های پوششی در توپولوژی برقرار شود.

![{\displaystyle |G\cdot x|=[G\,:\,G_{x}]=|G|/|G_{x}|,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb2cf9bb1f43b44e6798feefb9854929e9dcdc33)



 . کوچکترین مجموعههایی که میتوان روی آنها اعمال وفادار تعریف کرد به ترتیب در اندازههای 5، 12 و 16 هستند.
. کوچکترین مجموعههایی که میتوان روی آنها اعمال وفادار تعریف کرد به ترتیب در اندازههای 5، 12 و 16 هستند. همچنین
همچنین  (به
(به  ) اما دومی روی مجموعه ای با اندازه 2 n صادقانه عمل می کند، در حالی که اولی نمی تواند روی مجموعه ای کوچکتر از خودش صادقانه عمل کند.
) اما دومی روی مجموعه ای با اندازه 2 n صادقانه عمل می کند، در حالی که اولی نمی تواند روی مجموعه ای کوچکتر از خودش صادقانه عمل کند. محدود است
محدود است  بر
بر  توسط ترجمه ها سرگردان است. عمل
توسط ترجمه ها سرگردان است. عمل  محدود است اقدامات سرگردان ارائه شده در بالا نیز به درستی ناپیوسته هستند. از سوی دیگر، عمل از
محدود است اقدامات سرگردان ارائه شده در بالا نیز به درستی ناپیوسته هستند. از سوی دیگر، عمل از بر
بر  داده شده توسط
داده شده توسط  سرگردان و آزاد است اما به درستی ناپیوسته نیست.
سرگردان و آزاد است اما به درستی ناپیوسته نیست.  است
است  .
. 
 :
:

 سپس مدارها
سپس مدارها 
 اگر و فقط اگر چنین است
اگر و فقط اگر چنین است  برای تمام x در X (با توجه به اینکه X خالی نیست).
برای تمام x در X (با توجه به اینکه X خالی نیست). بر خلاف متغیرها (نقاط ثابت) که X G نشان داده می شود : متغیرهای متغیر یک ضریب هستند در حالی که متغیرها یک زیر مجموعه هستند . اصطلاحات و نمادهای متغیر به ویژه در هم شناسی
بر خلاف متغیرها (نقاط ثابت) که X G نشان داده می شود : متغیرهای متغیر یک ضریب هستند در حالی که متغیرها یک زیر مجموعه هستند . اصطلاحات و نمادهای متغیر به ویژه در هم شناسی  مجموعه را نشان می دهد
مجموعه را نشان می دهد  زیر مجموعه Y است گفته می شود ثابت تحت G اگر
زیر مجموعه Y است گفته می شود ثابت تحت G اگر (که معادل است
(که معادل است  ). در آن صورت، G نیز با محدود کردن عمل به Y روی Y عمل میکند . زیر مجموعه Y تحت G ثابت نامیده می شود اگر
). در آن صورت، G نیز با محدود کردن عمل به Y روی Y عمل میکند . زیر مجموعه Y تحت G ثابت نامیده می شود اگر برای همه g در G و Y در Y . هر زیر مجموعه که در زیر ثابت G است ثابت تحت G ، اما نه برعکس.
برای همه g در G و Y در Y . هر زیر مجموعه که در زیر ثابت G است ثابت تحت G ، اما نه برعکس. به طوری که
به طوری که  برای همه
برای همه  مجموعه همه x نشان داده می شود
مجموعه همه x نشان داده می شود و به نام G-ویژگیهای از X . هنگامی که X است
و به نام G-ویژگیهای از X . هنگامی که X است  گفته می شود که " X یک نقطه ثابت از g " یا این که " g رفع X ". برای هر x در X ،زیر گروه پایدار ساز ازGبا توجه بهX(همچنین به نامگروه همسانی و یاگروه کوچک
گفته می شود که " X یک نقطه ثابت از g " یا این که " g رفع X ". برای هر x در X ،زیر گروه پایدار ساز ازGبا توجه بهX(همچنین به نامگروه همسانی و یاگروه کوچک
 با
با  سپس دو گروه پایدار ساز
سپس دو گروه پایدار ساز  مرتبط هستند توسط
مرتبط هستند توسط  اثبات: طبق تعریف،
اثبات: طبق تعریف،  اگر و تنها اگر
اگر و تنها اگر  اعمال کردن
اعمال کردن  به هر دو طرف این برابری بازده
به هر دو طرف این برابری بازده  به این معنا که،
به این معنا که،  یک شمول متضاد به طور مشابه با گرفتن دنبال می شود
یک شمول متضاد به طور مشابه با گرفتن دنبال می شود  و با فرض
و با فرض 
 کلاس مزدوج H را نشان می دهد . سپس مدار O دارای نوع است
کلاس مزدوج H را نشان می دهد . سپس مدار O دارای نوع است













 یک
یک  و
و  اشیاء باشد
اشیاء باشد  به یک شیء همضرب می گویند
به یک شیء همضرب می گویند  نوشته شده است
نوشته شده است  یا
یا  یا گاهی اوقات به سادگی
یا گاهی اوقات به سادگی  در صورت وجود همریختی
در صورت وجود همریختی  و
و  ارضای
ارضای  و هرگونه همریختی
و هرگونه همریختی  و
و  یک همریختی منحصر به فرد وجود دارد
یک همریختی منحصر به فرد وجود دارد  به طوری که
به طوری که  و
و  یعنی نمودار زیر
یعنی نمودار زیر 
 ساخت این نمودار رفت و آمد ممکن است نشان داده شود
ساخت این نمودار رفت و آمد ممکن است نشان داده شود 

 یا
یا ![{\displaystyle \left[f_{1},f_{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad50929aab7cbf67b44632c8309dc398e3ff76dc) همریختی ها
همریختی ها  و
و 
 همضرب خانواده
همضرب خانواده  یک شی است
یک شی است  همراه با مجموعه ای از
همراه با مجموعه ای از  به طوری که برای هر شی
به طوری که برای هر شی  یک همریختی منحصر به فرد وجود دارد
یک همریختی منحصر به فرد وجود دارد  به طوری که
به طوری که  یعنی نمودار زیر برای هر کدام
یعنی نمودار زیر برای هر کدام  :
:
 اغلب نشان داده می شود
اغلب نشان داده می شود  یا
یا 
 برای نشان دادن وابستگی آن به فرد
برای نشان دادن وابستگی آن به فرد  س
س به
به  به طور کلی یک همضرب خواهد داشت، اما اگر داشته باشد، پس همضرب به معنای قوی منحصر به فرد است: اگر
به طور کلی یک همضرب خواهد داشت، اما اگر داشته باشد، پس همضرب به معنای قوی منحصر به فرد است: اگر  و
و  دو همضرب خانواده هستند
دو همضرب خانواده هستند  به طوری که
به طوری که  برای هر
برای هر  تابع
تابع  و به هر همریختی
و به هر همریختی  . سپس همضرب
. سپس همضرب که در
که در  از شی
از شی  که در
که در  .
. . همضرب خانواده
. همضرب خانواده به عنوان
به عنوان  مجموعه ای از تمام همریختی ها را نشان می دهد
مجموعه ای از تمام همریختی ها را نشان می دهد  به
به  که در
که در 



 به تنظیم پیوسته است. محدودیت ها را حفظ می کند (یک همضرب در
به تنظیم پیوسته است. محدودیت ها را حفظ می کند (یک همضرب در ، سپس همضرب اشیاء
، سپس همضرب اشیاء  اغلب با نشان داده می شود
اغلب با نشان داده می شود  . فرض کنید همه هم ضربs محدود در وجود C ، تابعگر ها هم ضرب اند همانطور که در بالا انتخاب شده است، و 0 نشان دهنده
. فرض کنید همه هم ضربs محدود در وجود C ، تابعگر ها هم ضرب اند همانطور که در بالا انتخاب شده است، و 0 نشان دهنده 


 ، سپس ما یک همریختی منحصر به فرد داریم
، سپس ما یک همریختی منحصر به فرد داریم  (از آنجا که
(از آنجا که  . از آنجا که
. از آنجا که مانند پاراگراف قبل بنابراین ما همریختی داریم
مانند پاراگراف قبل بنابراین ما همریختی داریم و
و  ، که توسط آن یک همریختی متعارف را استنباط می کنیم
، که توسط آن یک همریختی متعارف را استنباط می کنیم  . این ممکن است با القاء به یک همریختی متعارف از هر همضرب محدود به ضرب مربوطه گسترش یابد. این همریختی به طور کلی لازم نیست یک یکریختی باشد. در دورهای آن مناسب است
. این ممکن است با القاء به یک همریختی متعارف از هر همضرب محدود به ضرب مربوطه گسترش یابد. این همریختی به طور کلی لازم نیست یک یکریختی باشد. در دورهای آن مناسب است  به عنوان مجموعه اعداد حقیقی، سپس حاصلضرب مستقیم
به عنوان مجموعه اعداد حقیقی، سپس حاصلضرب مستقیم  فقط ضرب دکارتی است
فقط ضرب دکارتی است  .
. .
. .
. یک ندارد
یک ندارد  . این به این حقیقیت بستگی دارد که ضرب مستقیم
. این به این حقیقیت بستگی دارد که ضرب مستقیم  برای هر ساختار جبری
برای هر ساختار جبری  ،
،  ، و
، و  برای هر ساختار جبری
برای هر ساختار جبری  .
. .
.
 .
. متعارف
متعارف  . مجموع مستقیم و حاصلضرب مستقیم برای اندیس های نامتناهی یکریخت نیستند، جایی که عناصر یک مجموع مستقیم برای همه صفر هستند اما برای تعداد متناهی از ورودی ها. آنها در مفهوم
. مجموع مستقیم و حاصلضرب مستقیم برای اندیس های نامتناهی یکریخت نیستند، جایی که عناصر یک مجموع مستقیم برای همه صفر هستند اما برای تعداد متناهی از ورودی ها. آنها در مفهوم  و
و ، حاصلضرب مستقیم بی نهایت و مجموع مستقیم اعداد حقیقی. فقط دنباله هایی با تعداد متناهی از عناصر غیر صفر در Y هستند . به عنوان مثال، (1،0،0،0،...) در Y است اما (1،1،1،1،...) نیست. هر دوی این دنباله ها در ضرب مستقیم X هستند . در واقع، Y یک زیر مجموعه مناسب از X است (یعنی Y ⊂ X ).
، حاصلضرب مستقیم بی نهایت و مجموع مستقیم اعداد حقیقی. فقط دنباله هایی با تعداد متناهی از عناصر غیر صفر در Y هستند . به عنوان مثال، (1،0،0،0،...) در Y است اما (1،1،1،1،...) نیست. هر دوی این دنباله ها در ضرب مستقیم X هستند . در واقع، Y یک زیر مجموعه مناسب از X است (یعنی Y ⊂ X ). 


 با خودش ارتباطی ندارد (1،2) و (2،1).
با خودش ارتباطی ندارد (1،2) و (2،1). ،
، به i ام جزء آن g i .
به i ام جزء آن g i . و
و  ، می گوییم X یک ضرب مستقیم داخلی A و B است ، در حالی که اگر A و B فرعی نباشند، می گوییم که این یک ضرب مستقیم خارجی است.
، می گوییم X یک ضرب مستقیم داخلی A و B است ، در حالی که اگر A و B فرعی نباشند، می گوییم که این یک ضرب مستقیم خارجی است.




 .
.
 و
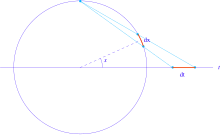
و  فاصله p مربوط به q تا مرکز دیسک است،
فاصله p مربوط به q تا مرکز دیسک است، فاصله بین ص و س ،
فاصله بین ص و س ، شعاع دایره مرزی دیسک و
شعاع دایره مرزی دیسک و  است
است  جایی که
جایی که  است
است  بین مبدا و نقطه قرار دارد
بین مبدا و نقطه قرار دارد  (یعنی دو نقطه در یک شعاع هستند، زاویه قطبی یکسانی دارند و
(یعنی دو نقطه در یک شعاع هستند، زاویه قطبی یکسانی دارند و ، فاصله هذلولی آنها است
، فاصله هذلولی آنها است . این به فرمول قبلی کاهش می یابد اگر
. این به فرمول قبلی کاهش می یابد اگر .
. دارای.)
دارای.)

 نشان دهنده هنجار اقلیدسی معمول است. سپس تابع فاصله است
نشان دهنده هنجار اقلیدسی معمول است. سپس تابع فاصله است



 که بدون پیچش است، یعنی معادله ماتریس را برآورده می کند
که بدون پیچش است، یعنی معادله ماتریس را برآورده می کند  . حل این معادله برای
. حل این معادله برای



 در مدل کلاین
در مدل کلاین در مدل دیسک پوانکاره
در مدل دیسک پوانکاره و فرمول ها تبدیل می شوند
و فرمول ها تبدیل می شوند  بنابراین نقاط ثابت هستند.
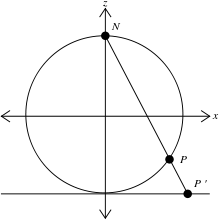
بنابراین نقاط ثابت هستند. یک بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل دیسک کلاین با:
یک بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل دیسک کلاین با:
 هنجار کمتر از یک نشان دهنده نقطه ای از مدل بلترامی-کلاین است، نقطه متناظر مدل دیسک پوانکاره به صورت زیر به دست می آید:
هنجار کمتر از یک نشان دهنده نقطه ای از مدل بلترامی-کلاین است، نقطه متناظر مدل دیسک پوانکاره به صورت زیر به دست می آید:

 در مدل نیمه هواپیما
در مدل نیمه هواپیما  در مدل دیسک
در مدل دیسک




![{\displaystyle {\begin{aligned}x^{2}+y^{2}&{}+{\frac {v_{1}(u_{2}^{2}+v_{2}^{2} +1)-v_{2}(u_{1}^{2}+v_{1}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}} x\\[8pt]&{}+{\frac {u_{2}(u_{1}^{2}+v_{1}^{2}+1)-u_{1}(u_{2}^ {2}+v_{2}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}}y+1=0\,.\end{تراز شده}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f65eb0e73ee28b703a59b3fdfcc8eb28facd52a6)


 )
)

































 .
. ،
، .
.













 که i و i + 1 را با هم عوض کنید .
که i و i + 1 را با هم عوض کنید .  تولید S N به روابط زیر است:
تولید S N به روابط زیر است: 
 برای |ij|>1}
برای |ij|>1} ، و
، و
 .
.

 مربوط به جابجایی غیر پیش پا افتاده، و
مربوط به جابجایی غیر پیش پا افتاده، و  به دلیل پوشش استثنایی 3 برابری) همسانی گروه متقارن را تغییر نمی دهد. پدیده های گروه متناوب پدیده های گروه متقارن را به دست می دهند - نقشه
به دلیل پوشش استثنایی 3 برابری) همسانی گروه متقارن را تغییر نمی دهد. پدیده های گروه متناوب پدیده های گروه متقارن را به دست می دهند - نقشه  گسترش می یابد به
گسترش می یابد به  و پوشش های سه گانه A 6 و A 7 به پوشش های سه گانه S 6 و S 7 گسترش می یابند - اما اینها همسان نیستند - نقشه \
و پوشش های سه گانه A 6 و A 7 به پوشش های سه گانه S 6 و S 7 گسترش می یابند - اما اینها همسان نیستند - نقشه \ جابجایی S 4 را تغییر نمی دهد و پوشش های سه گانه نیز با همسانی مطابقت ندارند.
جابجایی S 4 را تغییر نمی دهد و پوشش های سه گانه نیز با همسانی مطابقت ندارند.


 تعریف شده بر روی یک
تعریف شده بر روی یک  نمادها شامل
نمادها شامل  (
( است
است  .
. ،
،  ،
،  ،
،  ، و
، و  .
.  سپس نام ممکن است به اختصار باشد
سپس نام ممکن است به اختصار باشد  ،
،  ، یا
، یا  .
.  و
و  (
(  ). گروه S N است
). گروه S N است  . این بخش اساسی از اثبات
. این بخش اساسی از اثبات  وجود دارد
وجود دارد 






 ، این ویژگی اغلب برای به دست آوردن
، این ویژگی اغلب برای به دست آوردن 

 جابجایی (غیر مجاور).
جابجایی (غیر مجاور).





 ، تغییر پایه
، تغییر پایه  یک
یک  در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.