ادامه نوار موبیوس

باند Möbius با مرز گرد [ ویرایش ]

لبه ، یا مرز ، یک نوار Möbius همومورف (معادل توپولوژیک) به یک دایره است . تحت تعبیه معمول نوارها در فضای اقلیدسی ، مانند بالا ، مرز یک دایره واقعی نیست. با این وجود می توان نوار Möbius را در سه بعد تعبیه کرد تا مرز یک دایره کامل باشد که در بعضی از هواپیما قرار دارد. به عنوان مثال ، شکلهای 307 ، 308 و 309 "هندسه و تخیل" را ببینید. [13]

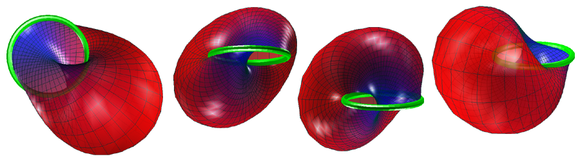
تعبیه هندسی بسیار بیشتر با یک بطری Klein حداقل غوطه ور در 3 کره آغاز می شود ، همانطور که Blaine Lawson کشف کرد. سپس نیمی از این بطری کلاین را می گیریم تا یک باند Möbius در 3-کره تعبیه شده (حوزه واحد در 4 فضا) بدست آوریم. نتیجه آن گاه به نام "سودانی مبیوس باند" خوانده می شود ، [14] که در آن "سودانی" به کشور سودان اطلاق نمی شود بلکه نام دو توپولوژیست به نام سو گودمن و دانیل آسیموف است. همانطور که در شکل زیر مشاهده می شود ، اعمال پیش بینی استریو باند سودان ، آن را در فضای سه بعدی قرار می دهد - نسخه ای به دلیل جورج فرانسیس را می توان در اینجا یافت .

از بطری Klein مینیمال لاوسون تعبیه باند را به درون 3- S S 3 می گیریم ، به عنوان زیرمجموعه ای از C 2 در نظر گرفته می شود ، که از نظر هندسی همانند R 4 است . ما زوایای η ، φ را به اعداد پیچیده z 1 و z 2 از طریق نقشه برداری می کنیم

$z_ {1} = \ sin \ eta \، e ^ {i \ varphi$

$z_ {2} = \ cos \ eta \، e ^ {i \ varphi / 2.$

در اینجا پارامتر η از 0 تا π اجرا می شود و φ از 0 تا 2 π اجرا می شود . از سال | z 1 | 2 + | z 2 | 2 = 1 ، سطح تعبیه شده کاملاً در S 3 قرار دارد . مرز نوار توسط | z 2 | = 1 (مربوط به η = 0 ، π ) ، که به وضوح دایره ای بر روی کره 3 است.

برای به دست آوردن تعبیه نوار Möbius در R 3 یکی از نقشه های S 3 تا R 3 را از طریق یک طرح ریزی استریوگرافی انجام می دهد . نکته طرح ریزی می تواند هر نقطه بر روی S 3 است که بر روی نوار موبیوس تعبیه شده دروغ است (این قوانین از تمام نقاط طرح معمول) است. یک انتخاب ممکن است $\ چپ \ {1 / {\ sqrt {2}} ، i / {\ sqrt {2}} \ Right \$ . پیش بینی های استریوگرافی نقشه ها را به دور دایره ها می کشد و مرز دایره ای نوار را حفظ می کند. نتیجه ، تعبیه صاف نوار Möbius به R 3 با لبه دایره ای و بدون تقاطع خود است.

باند سودانی مبیوس در سه حوزه S 3 از نظر هندسی یک دسته فیبر بر روی یک دایره بزرگ است که الیاف آن نیم دایره ای عالی است. متقارن ترین تصویر از طرح ریزی استریوگرافی این باند به R 3 با استفاده از یک نقطه طرح ریزی که بر روی آن دایره بزرگ قرار دارد که از قسمت میانی هر یک از نیم دایره ها قرار دارد ، بدست می آید. هر انتخاب از چنین نقطه طرح ریزی منجر به تصویری می شود که متناسب با سایرین باشد. اما از آنجا که چنین نقطه پیش بینی بر روی باند Möbius نهفته است ، دو جنبه تصویر به طور قابل توجهی با مورد تفاوت دارد (تصویر بالا) که در آن نقطه در باند نیست: 1) تصویر در R 3گروه کامل Möbius نیست ، بلکه گروهی است که یک امتیاز از آن خارج شده است (از خط اصلی آن). و 2) تصویر بدون مرز است - و هرچه از منشأ R 3 دورتر شود ، به طور فزاینده ای به هواپیما نزدیک می شود. با این حال ، این نسخه از تصویر stereographic دارای یک گروه از 4 تقارن در R 3 (آن را با کلاین 4 گروه ایزومورفیک است ) ، در مقایسه با نسخه محدود شده نشان داده شده در بالا با داشتن گروه تقارن خود ، گروه منحصر به فرد از نظم 2. (اگر همه تقارن ها و فقط ایزومترهای حفظ کننده جهت گیری R 3 مجاز هستند ، تعداد تقارنها در هر مورد دو برابر می شود.)

اما از لحاظ هندسی متقارن ترین نسخه باند اصلی سودانی مبیوس در سه حوزه S 3 است ، جایی که گروه کامل تقارن آن برای گروه Lie O (2) از نظر همسان است. با داشتن یک کاردینالیت بی نهایت (از پیوستار ) ، این به مراتب بزرگتر از گروه تقارن هرگونه تعبیه احتمالی باند مبیوس در R 3 است .

هندسه پروژه ای [ ویرایش ]

با استفاده از هندسه پروژکتور ، باند Möbius باز می تواند به عنوان مجموعه ای از راه حل های یک معادله چند جمله ای توصیف شود. اضافه کردن یک نابرابری چند جملهای منجر به باند بسته Möbius می شود. این باند Möbius به هندسه بسته های خط و عملیات منفجر شدن در هندسه جبری مربوط می شود .

خط پیش بینی واقعی $\ displaystyle \ mathbf {RP} ^ {1}}$ مجموعه است $\ displaystyle \ mathbf {R} ^ {2} \ setminus \ {(0،0) \}$ پوسته پوسته شدن مدول یعنی یک نکته در $\ displaystyle \ mathbf {RP} ^ {1}}$ یک کلاس هم ارزی فرم است

$\ displaystyle [A: B] = \ {(\ lambda A، \ lambda B): \ lambda \ in \ mathbf {R} \ setminus \ {0 \} \}.$

هر کلاس هم ارزی ${\ نمایشگر [A: B]$ با $\ displaystyle B \ neq 0$ یک نماینده منحصر به فرد دارد که مختصات دوم آن 1 است ${\ نمایش صفحه نمایش (A / B ، 1)}$ . این نقاط کپی از خط اقلیدسی را تشکیل می دهند $\ displaystyle \ mathbf {R} ^ {1}}$ . با این حال ، کلاس هم ارزی از ${\ نمایشگر [1: 0]$ چنین نماینده ای ندارد این نکته اضافی مانند بی نهایت نامعلوم رفتار می کند\ $\ displaystyle \ mathbf {RP} ^ {1}}$ از نظر توپولوژیکی همان دایره است $S ^ {1$ . مزیت $\ displaystyle \ mathbf {RP} ^ {1}}$ بیش از دایره این است که برخی از اشیاء هندسی از لحاظ معادلات ساده تر دارند $آ$ و $ب$ . این مورد برای گروه Mbibius است.

اجرای یک باند M bandbius باز توسط مجموعه داده شده است

$\ displaystyle M = \ {((x، y)، [A: B]) \ in \ mathbf {R} ^ {2} \ Times \ mathbf {RP} ^ {1}: Ax = By \.$

اگر خط را حذف کنیم \ نمایشگر x = 0 $x = 0$ از جانب $م$ (یا در واقع هر خط) ، پس از آن زیر مجموعه می تواند در فضای اقلیدسی تعبیه شود $\ mathbf {R} ^ 3$ . حذف این خط مجموعه را می دهد

${\ displaystyle {\ شروع {تراز شده} M '& = \ {((x ، y) ، [A: B]) \ in \ mathbf {R} ^ {2} \ Times \ mathbf {RP} ^ {1} : Ax = By، \ B \ neq 0 \} \\ & = \ {(x، y، m) \ in \ mathbf {R} ^ {3}: mx = y \}، \ end {تراز شده}}$

جایی که $م$ مطابق با $A / B$ .

باند بسته Möbius بسته به عنوان یک مجموعه مشابه وجود دارد ، اما با یک نابرابری اضافی برای ایجاد یک مرز:

$\ displaystyle N = \ {((x، y)، [A: B]) \ in \ mathbf {R} ^ {2} \ Times \ mathbf {RP} ^ {1}: Ax = By، \ x ^ 2} + y ^ {2} \ leq 1 \}.$

مرز $ن$ مجموعه تمام امتیازات با است $x ^ 2 + y ^ 2 = 1$ . هندسه از $ن$ بسیار شبیه به $م$ بنابراین ما روی آن تمرکز خواهیم کرد $م$ در ادامه

هندسه از $م$ را می توان از نظر منشأ خطوط توصیف کرد. هر خط از طریق مبدا در $\ mathbf {R} ^ 2$ مجموعه راه حل یک معادله است $ax \ نمایشگر تبر + توسط = 0$ . چه موقع مجموعه راه حل تغییر نمی کند $(الف ، ب)$ نجات می یابد ، بنابراین خط فقط به کلاس هم ارزی بستگی دارد ${\ نمایشگر [A: B]$ . یعنی خطوط از طریق مبدأ پارامتر می شوند $\ displaystyle \ mathbf {RP} ^ {1}}$ . علاوه بر این ، هر نکته $(x ، y)$ که در $\ mathbf {R} ^ 2$ ، بجز $(۰))$ ، از طریق منشاء ، به طور خاص ، خط تعریف شده توسط آن ، در یک خط منحصر به فرد قرار دارد ${\ displaystyle [-y: x]$ . نکته ${\ displaystyle (x، y) = (0،0)$ اما ، در هر خط از خاستگاه نهفته است. برای این نقطه ، معادله $Ax \ displaystyle Ax + By = 0$ انحطاط به $0 = 0$ . این همیشه درست است ، بنابراین هر ${\ نمایشگر [A: B]$ یک راه حل است در نتیجه مجموعه $م$ ممکن است به عنوان اتحادیه جداکننده مجموعه خطوط از طریق مبدأ توصیف شود. این همان اتحادیه خطوط از طریق مبدأ است ، به جز اینکه شامل یک نسخه از مبداء برای هر خط است. این نسخه های اضافی مبدأ نسخه ای از آن هستند $\ displaystyle \ mathbf {RP} ^ {1}}$ و حلقه مرکزی گروه مبیوس را تشکیل می دهند. این خط ها حكم گروه مبیوس را توصیف می كنند. این دیدگاه در $م$ این نمایشگاه هر دو به عنوان کل فضای بسته خط تاکولوژیکی است ${\ mathcal {O}} (- 1)$ بر $\ displaystyle \ mathbf {RP} ^ {1}}$ و همچنین منفجر شدن منشا در $\ mathbf {R} ^ 2$ .

برای دیدن نیمه پیچ در $م$ ، با این نکته شروع کنید $(1،0)$ که در $\ mathbf {R} ^ 2$ . این مربوط به یک نکته منحصر به فرد است $م$ ، برای مثال $\ displaystyle P = ((1،0) ، [0: 1])}$ . نیم دایره خلاف جهت عقربه ساعت را بکشید تا مسیری به وجود بیاید $م$ داده شده توسط $\ displaystyle \ gamma (t) = ((\ \ cos (2 \ pi t))، \ sin (2 \ pi t))، [- \ sin (2 \ pi t)، \ cos (2 \ pi t)] )}$ . مسیر متوقف می شود $\ displaystyle t = 1/2$ ، که در آن نقطه می دهد $\ displaystyle Q = ((- 1،0) ، [0: 1])}$ . بجز $پ$ و $س$ ، هر نقطه از مسیر از طریق منشا در یک خط متفاوت قرار دارد. از این رو $\ گاما (t)$ یک بار به دور دایره مرکزی سفر می کند $م$ . با این حال ، در حالی که $پ$ و $س$ در همان خط حكم قرار دارند ، آنها در طرف مقابل خاستگاه قرار دارند. این تغییر علائم جلوه جبری نیمه پیچ و تاب است.