بارسلون یکی از بهترین مقاصد برای سفرهای تحصیلی دبیرستان است، حتی بیشتر برای سفرهای هنری. این یک شهر جادویی و تقریباً باطنی است که در آن شگفتیها، بازیگوشی و رنگ را میتوان در هر گوشه و در هر خیابان مشاهده کرد، به خصوص در خیابانهایی - در واقع بسیاری - که آثار معمار کاتالانی آنتون گائودی در آن ظاهر میشود.
گائودی شهر بارسلونا را با کارهای دیوانه وار خود، با بی نظمی آشکار و تخیل بیش از حد، گلدوزی کرد. آثاری که تصادفی به نظر میرسند و میتوانند با فرمهای طبیعی بدون هیچ قاعدهای و بدون هیچ انسجامی ترکیب شده باشند. این حداقل برداشت یک چشم سطحی و ناکافی است! در واقع، گائودی با علم و دقت فراوان میسازد. ساخت و سازهای او تشریفات ریاضی و هندسی را تراوش می کند که اگر نگاه با اولین ضربه راضی نباشد آشکار می شود. در بارسلونا، ریاضیات در هر گوشهای است: در طاقهای سهموی پر زرق و برق کالج سانتا ترزا، کازا میلا و در سهمیها و طاقهای طاقها و سقفهای تقریباً تمام آثار گائودی (میتوانیم برخی از اینها را تحسین کنیم. نمونههایی در عکسهای همراه با این مقاله، توسط گلوریا کروچه، دانشآموز 4B از Istituto Statale d'Arte of Monza).
معمار اساساً از دو منحنی ریاضی استفاده می کند: سهمی و خط لوله و هر ترکیب ممکن بین این دو. بیایید به ویژگیها، تفاوتها و پتانسیلهای آن نگاهی بیندازیم و به طور خاص به دو مثال اشاره کنیم: کالج خواهران ترزیان و ساگرادا فامیلیا. دو معماری که اشکال ریاضی متفاوتی را با شکوه تمام ارائه می دهند.

کلیسای جامع دریا و مدلهای ثابت استفاده شده توسط گائودی (زنجیرههای وارونه)
سهمی و خط سیر در واقع دو مکان هندسی هستند. نام آنها به نمودارهای مربوط به آنچه در ریاضیات ما توابع می گوییم، اشاره دارد که با نوشتن: y = f(x) قابل بیان است. آنها همچنین دو پیکربندی با ثبات عالی از نقطه نظر تعادل هستند که حتی - اگر با هم ترکیب شوند - مقاومت در برابر استرس را افزایش می دهند.
نوآوری بزرگی که گائودی ارائه کرد، ساخت مدلهای استاتیک، از طریق استفاده ترکیبی از این دو منحنی بود که او با طراحی و ساخت وارونه آنها، پایداری آنها را کنترل کرد. فقط پس از تکمیل تحقیقات آنها را صاف کرد و از آنها استفاده کرد. راستش را میتوان در مطالعات مهندس پولنی که در اواخر قرن هجدهم در جریان بازسازی گنبد سنت پیتر از کاتناری برای کنترل پایداری دندهها استفاده کرد، نمونههایی برای این عمل یافت. از گنبد. پولنی همچنین از مدلهای وارونه استفاده کرد، همانطور که گائودی بعداً در مطالعات ساخت - به عنوان مثال - Sagrada Famiglia و Güell Chapel انجام داد. معمار کاتالانی با طناب هایی مدل هایی می سازد که کیسه های شن را به آن آویزان می کند. بسته به ترتیب آنها، رشته ها پیکربندی یک سهمی (اگر کیسه ها به طور یکنواخت در امتداد خط توزیع شده باشند، یعنی اگر کیسه ها از یک صفحه افقی یکسان باشند) یا یک طناب (اگر کیسه ها به طور یکنواخت در امتداد توزیع شده باشند) به خود می گیرند. خود منحنی).
در این سفر، در میان خیابانها و بناهای تاریخی شهر بارسلون، نمیتوان پلههای باشکوهی را که گائودی در کاخهایش و
در خانواده ساگرادا، وصیتنامه فرهنگی او ساخته، فراموش کرد. پلههای دسترسی به برجهای کلیسای جامع نمونهای باشکوه از هلیکوئید کمی مخروطی شکل را تشکیل میدهد که از نظر ادراکی - هم از بالا و هم از پایین - به عنوان یک مارپیچ لگاریتمی باشکوه خوانده میشود. تفاوت، تقریباً عرفانی و با تعبیری کمی عاشقانه، این است که (از بالا مشاهده می شود) مارپیچ براق و براق است، از پایین، ناهموار و ناهموار است که گویی می خواهد زیر راحتی "جاده سرازیری" را فریبنده کند. و جذاب است و می توان بدون زحمت سفر کرد در حالی که یک "جاده سربالایی" خسته کننده است و اصلاً جذاب نیست ... همه به راحتی قابل درک هستند به شرطی که با دقت زیاد نگاه کنید و مشاهده کنید.

طاق نماهای پارک گوئل و راهرو کالج ترزین
بدیهی است که یک منبع پایان ناپذیر الهام برای گائودی، اشکال طبیعی و رشد آنها هستند.
از من پرسیدند که چرا ستونهای شیبدار درست میکنی، من به آنها پاسخ دادم: «به همان دلیل که مسافر خسته وقتی میایستد، به چوب شیبدار تکیه میدهد، زیرا اگر آن را در جهت عمودی قرار میداد، آرام نمیگرفت». :
نمی توان لیست تمام معماری های موجود در بارسلونا و حاوی اشکال ریاضی یا هندسی را انجام داد. با قدم زدن در پارک گوئل، میتوانید مسیرهای پیچ در پیچی را تحسین کنید که با پیکربندی زمین و تپهها با تونلها، تکیهگاهها و حتی طاقهای باشکوه سازگار هستند. طبیعی است که تعجب کنیم که چگونه همه اینها می توانند در تعادل باشند. یک بار دیگر پاسخ را خود معمار به ما ارائه می دهد که می گوید: "یک ضرب المثل باستانی می گوید: divide et impera (تقسیم کن و پیروز خواهی شد). باید به گونه ای تلوتلو خورده شود که زمینی که به صورت پلکانی وزن دارد به نفع خود لوله هایی باشد که منشور را با سبدها خالی می کنند تا باعث ایجاد فشار مورب نشود و در عوض وزن عمودی مناسب ایجاد شود. با طاقها انجام میشود: به جای چند تکیهگاه و طاقهای بزرگ، تکیهگاههای زیادی مورد نیاز است که طاقها را به قطعات کوچک تقسیم میکنند، با هدف اجتناب از تقویتکنندههایی که مانع ساخت و ساز میشوند: مفهوم درختی است که تکیه میدهد، همه در ساگرادا وجود دارد. فامیلیا کسانی که حس سازندگی دارند و میخواهند با انتزاع علمی جبران کنند، بیهوده تلاش میکنند":
کل پارک گوئل با سازههای باربری مانند تکیهگاههای طبیعی برای حمایت و نابودی نیروهای جانبی "بذر شده است". "رابطه بین المان باربر و تکیه گاه، با توجه به ارتفاع و در صورت ساخت بسیار ساده، از قبل ثابت شده است. لازم است عناصر بیرون زده با عناصر ورودی مجدد ترکیب شوند، تا اطمینان حاصل شود که هر عنصر محدب، یعنی در نور کامل قرار می گیرد، یک عنصر مقعر، یعنی یک سایه، باید در جزئیات خود دقیق باشد، زیرا آنچه اهمیت دارد این است: منطقه سایه دار ممکن است هیچ جزئیاتی نداشته باشد.
در این بازدید ما حتی نمیتوانیم تراسهای خانهها (باتلو، میلا...) را فراموش کنیم که با دودکشهای رنگارنگ و نمادین و سیستمهای هوادهی ساخته شده از طریق اشکال هندسی مانند پارابولوئیدها و هایپربولوئیدها غنی شدهاند." پارابولوئید پدر تمام هندسه است - گائودی به شاگردانش توضیح می دهد - زیرا در آن برآمدگی های موازی (متعامد یا مایل) و شعاعی (قطبی) وجود دارد. با طرح ریزی شعاعی) و ثابت کردن زاویه به جای متغیر (اگر یک ژنراتور را به دور سیستم مقابل بچرخانید، و آن را در یک شیب ثابت نگه دارید، بیضی را به دست می آورید)
. به خصوص آثار گائودی، میتوان گفت که این فقط مربوط به گائودی نیست. کلیسایی که کاملاً توسط مردم و برای مردم ساخته شده و خواستار آن بودند و فقط مردم بر آن اقتدار داشتند. همانطور که گفته شد هیچ تأثیر معماری دیگری وجود نداشت و این باعث می شود که آن را به بهترین نمونه از به اصطلاح گوتیک کاتالان تبدیل کند. حاملان سنگ، باستایکسوس ها، روز به روز - تحت هدایت تحسین برانگیز مونتاگوت - کلیسای خود را ساخته بودند. "برنگور مونتاگوت - فالکونز در رمان تاریخی خود "کلیسای جامع دریا" می نویسد - محاسبه کرده بود که دقیقا در چه نقطه ای کلید باید طوری قرار می گرفت که: دنده های قوس ها کاملا به هم وصل شوند. او روزها با طناب و بند بین ده ستون مثلثی کشیده بود، از داربست شاقول انداخته بود و طناب ها و طناب هایی کشیده بود که از پایه های روی زمین تا آخرین داربست می رفت. روزها روی کاغذها خط خطی کرده بود، خراشیده بود تا دوباره روی آنها بنویسد. اگر کلید دقیقاً در محل قرار نمیگرفت، تلاش طاقها را پشتیبانی نمیکرد و اپید در معرض خطر فروریختن قرار میگرفت. سرانجام پس از هزاران محاسبه و بی نهایت نقشه، نقطه دقیقی را روی سکوی آخرین داربست مشخص کرده بود. اینجا بود که کلید باید نه یک اینچ جلوتر و نه یک اینچ جلوتر قرار می گرفت.»

شومینه های خانه های Battlò و Milà
در پایان، لازم است تمدن بزرگی را به یاد بیاوریم که شهر بارسلون در فئودالیسم کامل به بردگانی که موفق به فرار، پناه بردن به دیوارهای آن و کار آزادانه برای یک سال کامل می شدند، آزادی اعطا کرد.
این حس تمدن و آزادی را هنوز می توان امروز در خیابان های آن حس کرد، جایی که شهروندان آرام و نادیده از سراسر جهان در آن قدم می زنند، با رنگ های هر نقطه از جهان تقریباً به معماری چند رنگی که زینت می بخشد جان می بخشد - وجود ندارد. حتی در صورت لزوم وجود ندارد - شهری که قبلاً با نور خود می درخشد و همچنین زیبایی نور ریاضی را منعکس می کند.
| تمثیل |
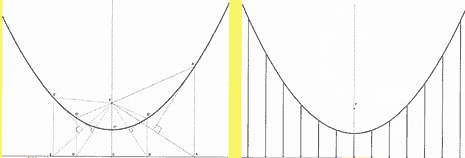
سهمی را به عنوان "مکان هندسی نقاطی که از یک نقطه و یک خط مستقیم فاصله دارند" می شناسیم. نقطه فوکوس و خط مستقیم نامیده می شود. برای توضیح این اصطلاحات، انجام یک بررسی مصنوعی در رابطه با تولید سهمی که به عنوان خطی که از تقاطع یک مخروط دایره ای نامعین با صفحه ای موازی با یکی از خطوط توصیف کننده سطح مخروط به دست می آید، تعریف می شود مفید خواهد بود. (این خطوط را خطوط مولد می نامند).
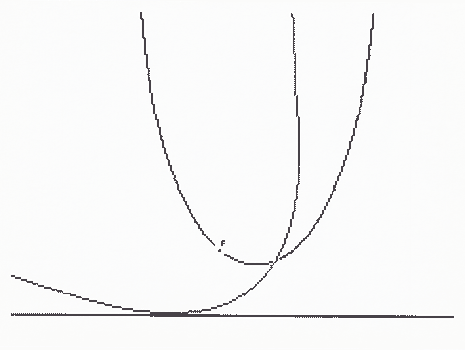
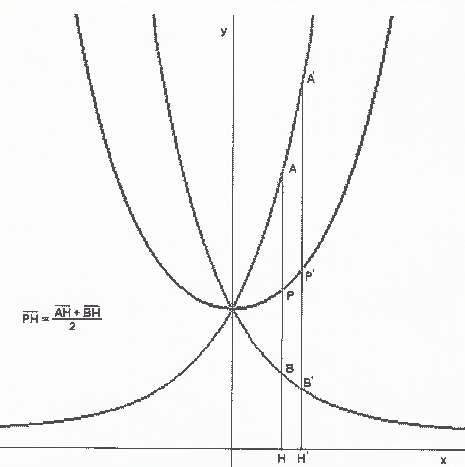
شکل 1 و شکل 2 از سهمی می توان منحنی دیگری را به صورت هندسی توصیف کرد: کاتناری. اجازه دهید سهمی را در امتداد یک خط مستقیم ترجمه و بچرخانیم. تمرکز مخروطی، در طول این تبدیل، کاتناری را توصیف می کند. به همین دلیل است که کاتناری به عنوان "غلت" سهمی تعریف می شود: یکی از غلت های مخروطی!
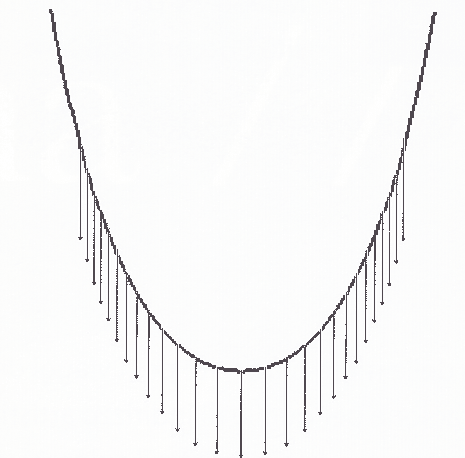
شکل 3 کاتینری از نظر تعادل دارای یک خاصیت بسیار مهم است: در معرض بار قرار گرفتن، وزن را به طور یکنواخت در امتداد منحنی توزیع می کند (هر نقطه تحت یک وزن قرار می گیرد!).
شکل 4 بدیهی است که پایداری در صورت استفاده از منحنی به دست آمده از ترکیب یک سهمی و یک خط لوله با هم تقویت می شود (این همان چیزی است که اغلب در پیکربندی پل های معلق اتفاق می افتد).
شکل 5 https://matematica.unibocconi.eu/articoli/matematica-barcellona |
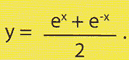
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.