توسط علی رضا نقش نیلچی
| جمعه بیست و هفتم خرداد ۱۴۰۱ | 22:33
- ما امروز بخش جدیدی را شروع می کنیم: حساب تغییرات. ما کمی در مورد میزبانی حساب تغییرات بحث می کنیم. چه چیزی متفاوت است؟ چرا ما به یک پارامتر متغیر نیاز داریم... و شرط را برای ماکزیمم کردن یک کمیت انتگرال اثبات می کنیم. نتیجه به معادلات اویلر معروف است.
- در نهایت از معادلات اویلر برای اثبات اینکه کوتاه ترین مسیر بین دو خط توسط یک خط مستقیم داده می شود استفاده می کنیم.
17.1 واقعاً حساب تغییرات چیست؟ 17.2 مسئله سریعترین فاصله یک شی 17.3 ما به یک پارامتر تغییر نیاز داریم. 17.4 معادلات اویلر: حذف مقدار انتگرال 17.5 مثال: کوتاهترین فاصله بین دو نقطه در صفحه دو بعدی
در چند سخنرانی اخیر، چندین حرکت کلاسیک را مورد بحث قرار دادیم و از مکانیک نیوتنی استفاده کردیم تا بفهمیم چگونه یک سیستم با زمان تکامل مییابد. همانطور که قبلاً بحث کردیم، قانون نیوتن یک قانون فیزیکی است و حق آن ثابت شده است. اما زمانی که دینامیک پیچیده می شود، اعمال قوانین نیوتن آسان نیست. روش های جایگزین در این زمینه مورد نیاز است.
یک روش جایگزین برای رسیدن به معادله حرکتی که توسط قانون نیوتن ارائه شده است، معادلات لاگران است. معادلات لاگرانژ بر اساس حساب تغییرات است.
محاسبات تغییرات اساساً راهی برای یافتن شرایط برای به حداقل رساندن یک کمیت معین که می تواند به عنوان یک انتگرال قابل بیان باشد، در اختیار ما قرار می دهد. اساساً شرایطی را برای به حداقل رساندن کمیت های فیزیکی پیدا می کنیم مانند: زمان، طول و غیره.
17.1 واقعاً حساب تغییرات چیست؟
مبحث حساب تغییرات یک مسئله در ریاضیات با سابقه طولانی است. ما می خواهیم شرایطی را برای به حداقل رساندن یک مقدار مشخص دریابیم. بدیهی است که از آنجایی که narure ترجیح می دهد مقادیر خاصی را از بین ببرد، این امر در زمینه های مختلف، از علوم بنیادی گرفته تا کاربردهای مالی، کاربرد دارد.
آیا نمیدانستیم که میتوانیم با در نظر گرفتن مشتق آن تابع با توجه به پارامتر تغییر و صفر کردن مشتق، مقدار را در مسئله خاص به حداقل برسانیم. خب..... بله، اما در اینجا ما قصد داریم توابع نه چندان ساده ای مانند f(x)، بلکه تابع هایی را در نظر بگیریم که می توان آنها را به صورت انتگرال روی برخی از متغیرها نوشت. بعداً در این مورد به تفصیل صحبت خواهیم کرد.
قبل از اینکه به جزئیات بپردازیم، اجازه دهید در مورد مشکلات تاریخی که منجر به توسعه این رشته حساب تنوع شده است صحبت کنیم.
17.2 مسئله سریعترین فاصله یک شی:
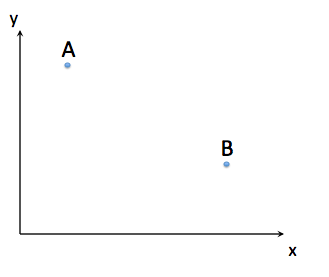
در یک میدان ثابت، مسیر بین دو نقطه را پیدا کنید. نقطه A و B، که به ذره اجازه می دهد در کمترین زمان حرکت کند. برنولی این مشکل را مطرح کرده است. چگونه پاسخی برای این مشکل پیدا کنیم؟ این مشکل به عنوان probelm Brachistochrone شناخته می شود. (در یونانی براکیستوس کوتاهترین و کرون زمان است) --- (تاریخ طولانی در مورد انتشار این مشکل در سال 1696 وجود دارد، پس از اینکه برنولی مشکل را ارائه کرد، پاسخ توسط نیوتن، برنولی (برادر برنولی که مشکل را ارائه کرد، ارسال شد. ) لایب نیتس و غیره ....
بعداً مشکلات دیگری به وجود آمد که در آن به حداقل رساندن یک کمیت انتگرال خاص مهم است. به عنوان مثال، در اپتیک، نور مسیر سریعترین زمان را طی می کند (که به عنوان اصل فرما شناخته می شود ). این یافته منجر به قوانین بازتاب و شکست شد.
بیایید در مورد مشکل کوتاه ترین فاصله صحبت کنیم، زیرا تجسم آن آسان تر است. کوتاه ترین فاصله بین دو نقطه چقدر است؟ خوب .... حالا شما جواب را می دانید ... اما تصور کنید ما نمی دانستیم ... چگونه آن را پیدا کنیم؟ این سوال مهم دیگری است که منجر به توسعه رشته حسابان تغییرات شد.
بیایید به مسئله کوتاهترین فاصله در یک صفحه دو بعدی فکر کنیم.
بیایید ببینیم چگونه می توانیم y(x) را پیدا کنیم، به طوری که فاصله بین دو نقطه در امتداد y(x) به حداقل برسد. بیایید معادله ای برای y(x) بنویسیم و سپس ببینیم چگونه می توانیم آن را به حداقل برسانیم.
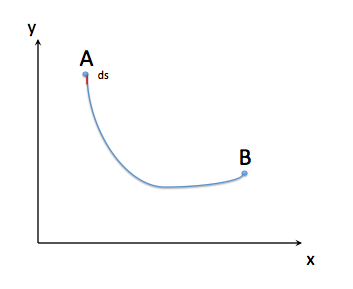
بیایید فاصله عنصری در طول یک مسیر تصادفی را ds بنویسیم که می تواند به صورت زیر نوشته شود:
بنابراین مجموع فاصله خواهد بود.
بنابراین، اکنون معادله ای برای فاصله کل بین دو نقطه A و B داریم. می خواهیم y(x) را پیدا کنیم، که فاصله s را به حداقل می رساند. چگونه آن را در فرمول بندی ریاضی قرار دهیم. ما فاصله را به عنوان تابعی از هیچ پارامتری نداریم، تا بتوانیم پارامتر را تنظیم کنیم تا فاصله را به حداقل برسانیم. به عبارت دیگر، اگر یک پارامتر داشتیم، میتوانیم فاصله کل دو نقطه را به عنوان تابعی از پارامتر بنویسیم و سپس مشتق کمیتی را که میخواهیم کمینه کنیم نسبت به این پارامتر گرفته و آن را به صفر
17.3 ما به یک پارامتر تنوع نیاز داریم.
پارامتر چه کاری انجام می دهد؟ پارامتری را معرفی می کنیم که بتوانیم کمیت انتگرال را در همسایگی تابع بهینه جستجو کنیم. به عنوان مثال، اگر مسئله کوتاهترین فاصله باشد، همه مسیرهای ممکن را جستجو میکنیم (که با یک پارامتر تغییر میکنند) و سپس به دنبال مسیری میگردیم که کوتاهترین فاصله را میدهد.
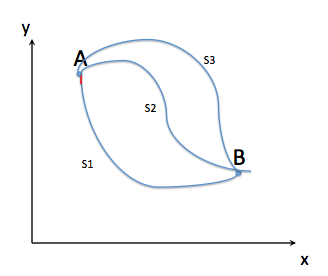
شما می توانید این وضعیت را به صورت ریاضی به صورت زیر نشان دهید.
در شکل بالا S1، S2، S3 سه فاصله کل ممکن است. مانند عاقلانه، میتوانیم مسیر را تغییر دهیم و به دنبال منحنی باشیم که حداقل S را میدهد.
اجازه دهید این وضعیت را در فرمولهای ریاضی قرار دهیم.
اساسا، y(alpha، x) تمام توابع ممکن را به عنوان یک نمایش پارامتریک ارائه می دهد. با تغییر پارامتر alpha، تمام اشکال ممکن توابع y(alpha,x) را پوشش می دهیم.
تابعفقط بین دو نقطه x1 و x2 تعریف می شود.
یک تابع صاف بین دو نقطه انتهایی
است. برای alpha=0 تابع صحیح را بدست می آوریم.
17.4 معادلات اویلر: حذف کمیت انتگرال
اکنون با استفاده از این تعریف با پارامتر تغییرات، می توانیم کمیت انتگرال را تعریف کنیم، مانند فاصله. بیایید کمیت انتگرال را J بنامیم.----------------(17.1)
تعریف کرده ایم:
حال با جایگزینی اینها در معادله. (17.1):
--------------(17.2)
برای ساده سازی قسمت دوم، می توانیم از انتگرال توسط قطعات استفاده کنیم،
بنابراین جمله اول در معادلات بالا به صفر می رسد، زیرا ما تابع متغیر را برای رفتن به صفر در نقاط پایانی انتخاب کردیم.
سپس داریم:--------------(17.3)
با ترکیب معادلات (17.2) و (17.3)، به دست می آید:
بنابراین، شرط را برای منتهی کردن کمیت انتگرال J به صورت زیر بدست می آوریم،------------ (17.4)
این معادله به معادله اویلر معروف است که شرط لازم برای به حداکثر رساندن J است.
اکنون شرایط را برای ماکزیمم کردن J می دانیم، با این حال، در مورد چگونگی تعریف J، x، y، y و غیره صحبت نکرده ایم.
برای اعمال معادلات اویلر، باید متغیر مستقل x را شناسایی کنیم و تابع باید باشد. به حداقل رساند.
بیایید چند مثال بزنیم:
17.5 مثال: کوتاه ترین فاصله بین دو نقطه در صفحه دو بعدی
اکنون می خواهیم از معادله اویلر برای یافتن فاصله بین دو نقطه در یک صفحه استفاده کنیم.
برای اعمال معادلات اویلر، باید مسئله را تعریف کنیم. مقداری که باید به حداقل برسد فاصله است. بیایید فاصله را به عنوان یک کمیت انتگرال بنویسیم.
طول عنصری 2 بعدی است را می توان به صورت زیر نوشت:
طول کل بین دو نقطه پس از آن خواهد بود،
حال بیایید از معادلات اویلر برای به حداقل رساندن s استفاده کنیم. با مقایسه با اثبات فوق معادلات اویلر:
بیایید از معادلات اویلر استفاده کنیم:
ما در بالا ثابت کردیم که کوتاه ترین مسیر بین دو نقطه را می توان به صورت y=mx+c نوشت که می دانیم یک خط مستقیم است. ما اساساً از معادله اویلر برای اثبات شرایط شناخته شده در اینجا استفاده کرده ایم. ما می دانستیم که کوتاه ترین مسیر بین دو نقطه در یک صفحه یک خط مستقیم است.
https://www2.physics.siu.edu/people/jayasekera/teaching/310/310_Lec17.html
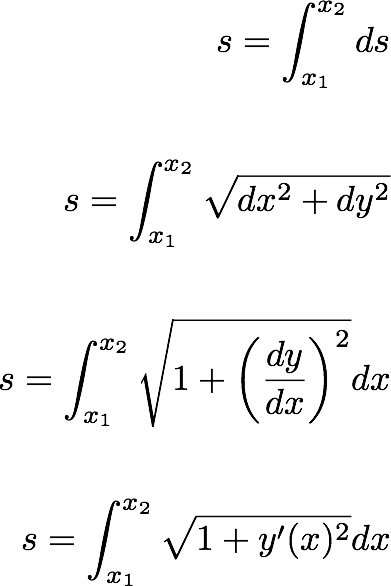
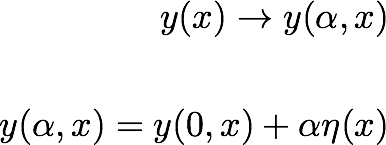
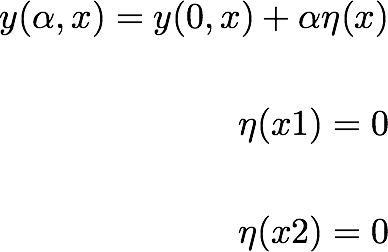
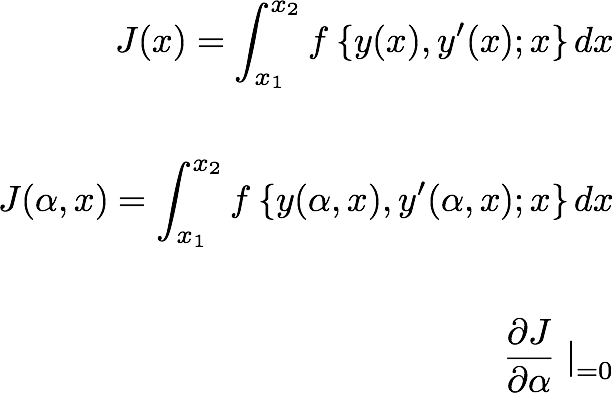
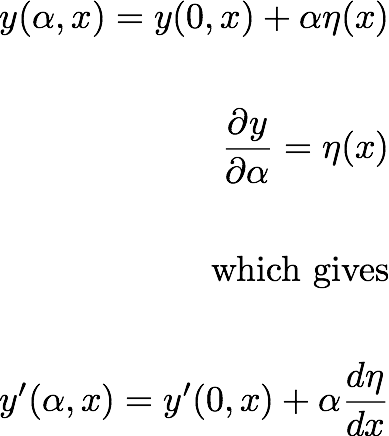
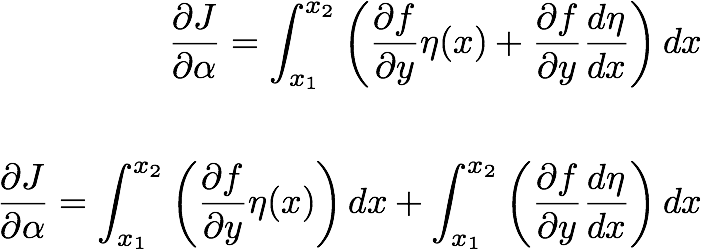
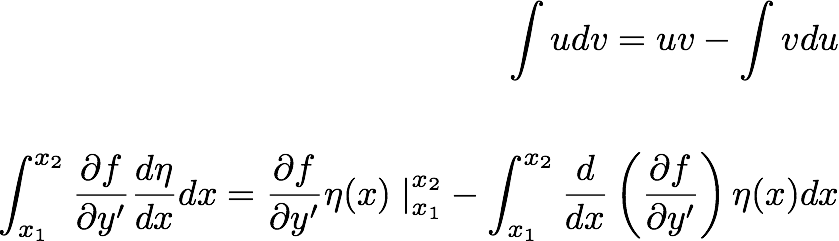
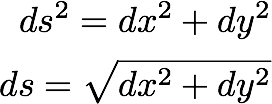
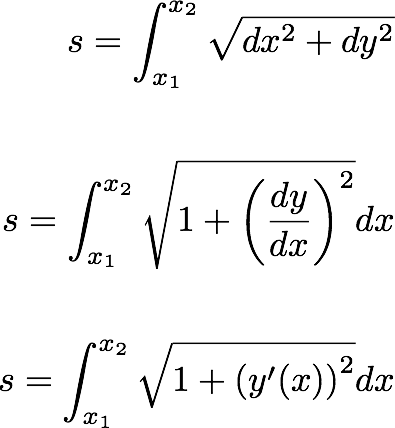
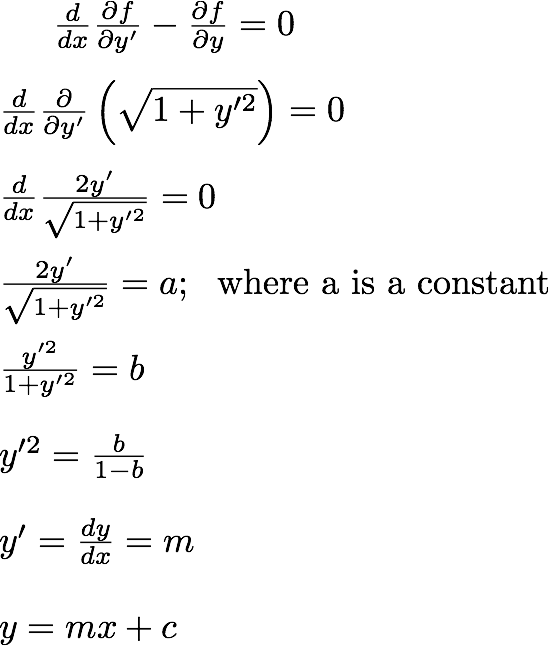
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.