ریاضیات

مقدمه و تعریف تبدیل لاپلاس، توابع رانندگی غیر استاندارد، حل از حوزه جبر. مثال های تبدیل لاپلاس، f(t)=1، f(t)=t. مثال های تبدیل لاپلاس f(t)= e t و f(t)= sin(2t). تبدیل لاپلاس یک عملگر خطی است، یک مثال، یک خطای کتاب در ویرایش هفتم، جدول کوچک تبدیل ها. لاپلاس هستی را تبدیل می‌کند، مثالی از تبدیل یک تابع تعریف‌شده تکه‌ای. لاپلاس مثال را با استفاده از خطی بودن تبدیل تبدیل می کند

در مدل مرتبه دوم خطی برای سیستم های فنر/جرم و مدار الکتریکی سری، سمت راست معادلات

یک "تابع محرک" است که مقداری نیروی خارجی f(t) یا یک ولتاژ تحت تاثیر E(t) را نشان می دهد. عملکردهای انتقال پیوسته تکه ای غیر معمول نیستند. به عنوان مثال، عملکرد انتقال را می توان به صورت گرافیکی با یکی از موارد زیر توصیف کرد:

ما هیچ روش مستقیمی برای حل مشکلات از این نوع نداریم. مشکلات را اغلب می توان با روش های تبدیل حل کرد و موردی که ما روی آن تمرکز خواهیم کرد تبدیل لاپلاس است.

تا زمانی که به درس 5 واحد V نرسیم، هیچ معادله دیفرانسیل را به این روش حل نمی کنیم. قبل از آن، باید یاد بگیریم که چگونه تبدیل و همچنین تبدیل معکوس توابع مختلف را ایجاد کنیم. تصویر زیر نحوه حل معادلات را نشان می دهد. برای بقیه این بخش و همچنین سه بخش بعدی، نحوه تبدیل و یافتن تبدیل معکوس توابع (فلش های کناری در تصویر) را یاد خواهیم گرفت.

از روش تبدیل لاپلاس می توان برای حل سیستم معادلات نیز استفاده کرد. 

Def: تبدیل لاپلاس : اگر f تابعی باشد که برای . 

توجه داشته باشید که تابعی از s است. یعنی L {f(t)}=F(s).

به نماد آشنای بزرگ کردن برای نشان دادن یک ضد مشتق توجه کنید.

مثال یافتن L {1}.

راه حل:

اگر M{Af(x)+Bg(x)}=AM{f(x)}+BM{g(x)} یک عملگر M خطی باشد.

توجه داشته باشید که تبدیل لاپلاس یک عملگر خطی است زیرا انتگرال خطی است:

مثال 1. L {t+2} را پیدا کنید

بعد از اینکه خودتان آن را امتحان کردید 

مثال 2. L {e 2t } را پیدا کنید (آسان تر!)

 بعد از اینکه خودتان آن را امتحان کردید 

یک سوال طبیعی مطرح می شود، به خصوص که یک تابع ساده برای یافتن تبدیل لاپلاس خود به محاسبه پیچیده نیاز دارد. آیا تبدیل لاپلاس همیشه برای یک تابع وجود دارد؟

Def: مرتبه نمایی اگر ثابت های C، M>0 و T>0 وجود
داشته باشد به تابع f از مرتبه نمایی C گفته می شود به طوری که برای همه t>T.

اگر f تابع افزایشی باشد، مرتبه نمایی C>0 بودن به این معنی است که نمودار f سریعتر از نمودار Me Ct برای t>T رشد نمی کند.

اگر f تابع نزولی باشد، مرتبه نمایی C<0 بودن به این معنی است که نمودار f زیر نمودار Me Ct برای t>T قرار دارد.

قضیه: شرایط کافی برای وجود اگر f(t) به صورت تکه ای پیوسته روی [0، بی نهایت) و از مرتبه نمایی C برای t>T باشد، آنگاه L {f(t)} برای s>C وجود دارد.

اثبات در این کتاب است و بر این تکیه دارد که نشان دهد انتگرالی که تبدیل لاپلاس را نشان می دهد همگرا است اگر از مرتبه نمایی C باشد. این نیاز به مقایسه انتگرال نشان دهنده تبدیل و انتگرال Me Ct دارد.

توجه داشته باشید که L {f(t)} برای f(t)=1/t یا f(t)=exp(t ^2 ) وجود ندارد. 

مثال نشان دهید که L {t n }=n!/s n+1 .

راه حل: با u=t n و du=nt n-1 ، dv=e -st و v=-e -st /s با استفاده از انتگرال توسط قطعات،

قسمت اول این را می توان با n+1 کاربرد قانون L'Hopital صفر نشان داد . 

حالا باید ارزیابی کنیم

همین روند ادامه خواهد داشت و آخرین انتگرال L {1}=1/s را از مثال قبل نشان می‌دهد.

مثال یافتن L {sin(kt)}

L {sin(kt)}=

انتگرال در مرحله اول توسط قطعات با u=sin(kt)، du=kcos(kt)، dv=e -st dt، v=-(1/s)e -st بود.

قسمت u*v=0 از sin(0)=0. با انتگرال باقی مانده ادامه دهید:

L{sin(kt)}=

ادغام در مرحله اول توسط قطعات با u=cos(kt)، du=-ksin(kt)، dv=e -st ، v=-(1/s)e -st بود.

قسمت u*v k/s 2 است (اگر حد را در بی نهایت محاسبه کنید، صفر است. cos(0) و e 0 هر دو 1 هستند، بنابراین ما –(-1) داریم.

مشکل اکنون در این مرحله است:

.

این معادله را می توان برای انتگرال مورد نظر حل کرد:

بنابراین می بینیم که L {sin(kt)}= .

به عنوان یک تکلیف، از شما خواسته می شود که L {cos(kt)} را انجام دهید. شبیه.

جدول زیر لیست بسیار کوتاهی از تبدیل های لاپلاس رایج است:

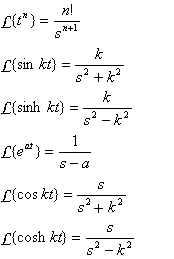
همانطور که مثال زیر نشان می دهد، توابع تعریف شده به صورت تکه ای دارای تبدیل لاپلاس هستند:

مثال تبدیل لاپلاس f(t) را پیدا کنید که در آن

راه حل:

از آنجایی که تابع به صورت تکه ای تعریف شده است، به سه انتگرال نگاه می کنیم:

نیازی به حفظ نمودار تبدیل نیست. می‌خواهم از این جلسه با یک مرور کلی، تعریف تبدیل، و برخی مهارت‌های یکپارچه‌سازی از کلاس حساب دیفرانسیل و انتگرال را مرور کنید.

وقتی چند قانون برای تبدیل ها بدانیم، می توانیم از خطی بودن تبدیل لاپلاس برای حل مسائل به راحتی استفاده کنیم.

مثال L {f(t)}که در آن f(t)=3t 2 +sint را پیدا کنید

راه حل:

L {3t 2 }=3(2!)/s 3 و L {sint}=1/(s 2 +1)، بنابراین داریم

L {3t 2 +sint }= 

حالا شما یکی را امتحان کنید:

مثال 3. L {f(t)} را پیدا کنید که در آن f(t)= t-7-cosht

منبع

http://donrmath.net/difeq/unit_5/lesson1/u5l1a.html