مقدمه [ ویرایش ]

انتگرال یک تابع مثبت f بین محدوده a و b را می توان به عنوان منطقه زیر نمودار f تعبیر کرد . این کار برای عملکردهای آشنا مانند چند جمله ای آسان است ، اما برای عملکردهای عجیب و غریب تر چیست؟ به طور کلی ، "ناحیه زیر منحنی" برای کدام کلاس از توابع معنی می دهد؟ پاسخ به این سؤال از اهمیت نظری و عملی بسیار برخوردار است.

به عنوان بخشی از یک حرکت کلی به سمت سخت گیری در ریاضیات در قرن نوزدهم ، ریاضیدانان کوشیدند محاسبات انتگرال را در یک پایه محکم قرار دهند. جدایی ناپذیر ریمان -proposed توسط برنهارد ریمان (1826-1866) -is تلاش گسترده موفق به ارائه چنین پایه و اساس. تعریف ریمان با ساختن دنباله ای از مناطق به راحتی محاسبه می شود که به انتگرال یک عملکرد معین همگرا می شوند. این تعریف به این معنی موفقیت آمیز است که جواب بسیاری از مشکلات از قبل حل شده را می دهد و برای بسیاری از مشکلات دیگر نتایج مفیدی را ارائه می دهد.

با این حال ، ادغام ریمان با در نظر گرفتن محدودیت توالی توابع ، تعامل خوبی ندارد ، و تجزیه و تحلیل چنین فرآیندهای محدود کننده را دشوار می کند. این مهم است ، به عنوان مثال ، در مطالعه سریال فوریه ، تبدیل فوریه و مباحث دیگر. انتگرال لبگ بهتر قادر به توصیف چگونگی و زمان امکان محدود کردن زیر علامت انتگرال است (از طریق قضیه همگرایی یکتایی قدرتمند و قضیه همگرایی تحت سلطه ).

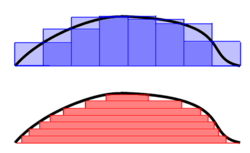
در حالی که انتگرال ریمان مساحت زیر منحنی را خارج از مستطیل های عمودی می داند ، تعریف لبگ دال های افقی را در نظر می گیرد که لزوما فقط مستطیل نیستند ، و بنابراین انعطاف پذیر تر است. به همین دلیل ، تعریف Lebesgue امکان محاسبه انتگرال ها برای یک کلاس گسترده تر از توابع را ممکن می سازد. به عنوان مثال ، عملکرد Dirichlet ، که 0 است که در آن استدلال آن غیر منطقی و 1 در غیر این صورت است ، دارای انتگرال لبگ است ، اما انتگرال Riemann ندارد. علاوه بر این ، انتگرال لبگاز این عملکرد صفر است ، که با این تصور موافق است که هنگام انتخاب یک عدد واقعی به طور یکنواخت به طور تصادفی از فاصله واحد ، احتمال انتخاب یک عدد منطقی باید صفر باشد.

لسبز در نامه ای به پل مونتل رویکرد خود برای ادغام را خلاصه کرد :

باید مبلغ مشخصی را بپردازم که در جیبم جمع کردم. قبض ها و سکه ها را از جیبم می گیرم و به منظور یافتن آنها ، تا زمانی که به جمع کل نرسم ، به طلبکار می دهم. این انتگرال ریمان است. اما من می توانم متفاوت عمل کنم. بعد از اینکه کلیه پول را از جیب خود برداشت کردم ، صورتحساب و سکه را طبق مقادیر یکسان سفارش می دهم و سپس چندین پشته یکی پس از دیگری به طلبکار می پردازم. این انتگرال من است.

-  منبع : ( Siggmund-Schultze 2008 )

بینش این است که باید بتواند مقادیر یک عملکرد را آزادانه مرتب کند و در عین حال ارزش انتگرال را حفظ کند. این فرآیند بازآرایی می تواند یک عملکرد بسیار آسیب شناختی را از منظر ادغام به یک "خوب" تبدیل کند ، و بنابراین اجازه می دهد چنین کارکردهای آسیب شناختی یکپارچه شوند.

تفسیر شهودی [ ویرایش ]

ادغام ریمان-داربوکس (به رنگ آبی) و ادغام لسبز (به رنگ قرمز).

برای درک برخی روشهای مختلف در مورد ادغام ، بگذارید تصور کنیم که می خواهیم حجم کوه (بالاتر از سطح دریا) پیدا کنیم.

رویکرد ریمان - داربوکس

پایه کوه را به صورت مربع 1 متر تقسیم کنید. ارتفاع کوه را در مرکز هر مربع اندازه بگیرید. حجم بر روی یک مربع شبکه واحد حدود 1 متر است 2 × (ارتفاع آن مربع است)، بنابراین حجم کل 1 متر است 2 برابر مجموع ارتفاعات.

رویکرد لبگ

نقشه کانتور کوه را بکشید ، جایی که کانتورهای مجاور از فاصله 1 متری از یکدیگر قرار دارند. حجم زمینی که یک کانتور منفرد در آن قرار دارد تقریباً 1 متر مربع است (مساحت کانتور) ، بنابراین حجم کل مبلغ این مناطق برابر 1 متر است.

Folland اختلاف بین رویکردهای ریمان و لبگ را خلاصه می کند: "برای محاسبه انتگرال ریمان از f ، یک قسمت دامنه [ a ، b ] را به زیر شاخه ها تقسیم می کند" ، در حالی که در انتگرب لبگ ، "یکی از قسمت های واقعی در واقع تقسیم بندی F است. "" [1]

به سمت تعریف رسمی [ ویرایش ]

یک عملکرد قابل اندازه گیری همراه با مجموعه نشان داده شده است\ displaystyle \ {x | f (x)> t \}(در محور x) انتگرال لبگ با برش در امتداد محور y ، با استفاده از اندازه گیری 1 بعدی Lebesgue برای اندازه گیری "عرض" برش ها بدست می آید.

برای تعریف انتگرال لبگ نیاز به مفهوم رسمی از یک اندازه گیری که، تقریبا، همکاران به هر مجموعه از اعداد حقیقی نامنفی تعداد μ ( ) به نمایندگی از "اندازه" از . این مفهوم "اندازه" باید با طول معمول یک بازه یا اتحاد ناپیوستگی فواصل مطابقت داشته باشد. فرض کنید f  :: → ℝ + تابعی با ارزش واقعی غیر منفی است. با استفاده از "پارتیشن بندی وسیعی از F " فلسفه، انتگرال F باید مجموع بیش از تی از منطقه ابتدایی موجود در نوار افقی نازک بین Y = Tو y = t - dt . این منطقه ابتدایی درست است

\ mu \ سمت چپ (\ {x \ میانه (x)> t \} \ راست) \ ، dt.

اجازه دهید

f ^ {*} (t) = \ mu \ left (\ {x \ mid f (x)> t \} \ Right).

انتگراللبگ از f با تعریف [2]

\ int f \، d \ mu = \ int _ {0} ^ {\ infty} f ^ {*} (t) \، dt

جایی که انتگرال سمت راست یک انتگرال نادرست ریمان است . توجه داشته باشید که F * غیر منفی کاهش عملکرد است، و در نتیجه تا جدایی ناپذیر ریمان نامناسب به خوبی تعریف شده با ارزش در فاصله [0، ∞] . برای یک کلاس مناسب از توابع ( توابع قابل اندازه گیری ) ، این انتگرال لبگ را تعریف می کند.

یک ژنرال (لزوما مثبت نیست) اندازه گیری عملکرد F لبسگو انتگرال است اگر منطقه بین نمودار F و X محور است محدود:

\ int | f | \، d \ mu <+ \ infty.

در این حالت ، مانند پرونده ریمانی ، انتگرال تفاوت بین منطقه بالای x -axis و منطقه زیر x -axis است:

\ int f \، d \ mu = \ int f ^ {+} \، d \ mu - \ int f ^ {-} \، d \ mu

جایی کهf = f ^ {+} - f ^ {-}تجزیه f به تفاوت دو عملکرد غیر منفی است که توسط

\ displaystyle {\ آغاز {هماهنگ شده} {3} f ^ {+} (x) & = \ max \ {f (x) ، 0 \} & {} = {} & {\ شروع {موارد} f (x ) ، & {\ text {اگر} f (x)> 0 ، \\ 0 ، و {\ متن {در غیر این صورت}} \ end {موارد} \ \\ f ^ {-} (x) & = \ max \ {-f (x) ، 0 \} & {} = {} & {\ شروع {موارد} -f (x) ، و {\ متن {اگر}} f (x) <0 ، \\ 0 ، و \ متن {در غیر این صورت.}} \ end {موارد}} \ پایان {تراز وسط}}}

منبع

https://en.wikipedia.org/wiki/Lebesgue_integration