یافتن روز رستاخیز یک سال [ ویرایش ]

ابتدا روز قرن را لنگر بزنید. برای اهداف روز رستاخیز ، یک قرن با '00 آغاز می شود و با '99 پایان می یابد. جدول زیر روز لنگر قرون 1800-1899 ، 1900-1999 ، 2000-2099 و 2100-22199 را نشان می دهد.

قرنروز لنگرحفظیفهرست (روز هفته)
1800-1899جمعه-5 (پنج روز)
1900-1999چهار شنبهما روز به روز
(بیشتر افراد زنده در آن قرن متولد شدند)		3 (سه شنبه)
2000-2099سهشنبهY-Tue-K یا Twos-day
( Y2K در رأس این قرن بود)		2 (دوشنبه)
2100–2199یکشنبهبیست و یک روز یکشنبه است
(2100 شروع قرن بعدی است)		0 (غیر روز)

بعد ، روز رستاخیز سال را پیدا کنید. برای انجام این کار مطابق Conway:

  1. تقسیم دو رقم آخر سال (پاسخ این Y ) 12 و اجازه دهید باشد کف از خارج قسمت .
  2. بگذارید b باقی مانده از همان مقدار باشد.
  3. آن باقیمانده را با 4 تقسیم کرده و بگذارید c قسمت کف باشد.
  4. بگذارید d از جمع سه عدد باشد ( d = a + b + c ). (مجدداً در اینجا امکان تقسیم بر هفت و تعداد باقیمانده وجود دارد. این عدد همانطور که باید باشد معادل جمع دو رقم آخر سال است که بصورت جمعی به علاوه کف آن رقم های جمعی تقسیم بر چهار تقسیم می شود.)
  5. برای دریافت روز رستاخیز سال تعداد روزهای مشخص شده ( d یا باقی مانده d/7 ) را از روز لنگر حساب کنید.

\ fill {matrix left \ left ({\ left \ lfloor {\ frac {y} 12}} \ Right \ rfloor + y \ bmod 12+ \ left \ lfloor {\ frac {y \ bmod 12 12 {4} \ right \ rfloor} \ Right) \ bmod 7+ \ rm {anchor} = \ rm {روز رستاخیز} \ end {ماتریس}

مثلاً برای قرن بیستم 1966:

\ شروع ماتریس} \ سمت چپ ({\ چپ \ lfloor {\ frac {66} 12}} \ Right \ rfloor + 66 \ bmod 12+ \ left \ lfloor {\ frac {66 \ bmod 12} {4} \ right \ rfloor} \ right) \ bmod 7+ \ rm {چهارشنبه} & = & & سمت چپ (5 + 6 + 1 \ سمت راست) \ bmod 7+ \ rm {چهارشنبه} \\ \ & = = & \ rm {دوشنبه } \ end {ماتریس

همانطور که در گلوله 4 در بالا توضیح داده شده است ، این معادل است:

\ شروع {ماتریس} \ چپ (66 + + \ چپ \ lfloor {\ frac {66} {4}} \ Right \ rfloor} \ Right) \ bmod 7+ \ rm {چهارشنبه} & = & \ چپ (66+ 16 \ درست) \ bmod 7+ \ rm {چهارشنبه} \\ \ & = & \ rm {دوشنبه} \ پایان {ماتریس

بنابراین روز رستاخیز در سال 1966 روز دوشنبه سقوط کرد.

به همین ترتیب ، روز رستاخیز در سال 2005 دوشنبه است:

\ سمت چپ ({\ چپ \ lfloor {\ frac {5} 12}} \ Right \ rfloor + 5 \ bmod 12+ \ left \ lfloor {\ frac {5 \ bmod 12} {4}} \ Right \ rfloor} \ درست) \ bmod 7+ \ rm {سه شنبه} = \ rm {دوشنبه

چرا کار می کند [ ویرایش ]

قانون رستاخیز

محاسبه روز رستاخیز بطور موثر تعداد روزهای بین هر تاریخ معین در سال پایه و همان تاریخ در سال جاری را محاسبه می کند ، سپس با استفاده از مدول باقیمانده 7. هنگامی که هر دو تاریخ بعد از روز جهش (در صورت وجود) می آیند ، تفاوت در این است. فقط 365 y + y/4 (دور تا دور). اما 365 برابر 1 + 7 52 52 است ، بنابراین پس از گرفتن باقیمانده درست می شویم

\ سمت چپ (y + \ left \ lfloor \ frac {y} 4} \ Right \ rfloor \ Right) \ bmod 7.

اگر راحت باشید مقادیر زیادی از y را با 4 و 7 تقسیم کنید ، فرمول ساده تری می دهد . برای مثال می توانیم محاسبه کنیم

\ سمت چپ (66 + \ چپ \ lfloor \ frac {66} 4} \ Right \ rfloor \ Right) \ bmod 7 = (66 + 16) \ bmod 7 = 82 \ bmod 7 = 5

که همان جواب را در مثال بالا می دهد.

جایی که 12 وارد می شود این است که الگوی ( y + ⌊ y/4 ⌋) mod 7 تقریباً هر 12 سال یکبار تکرار می شود. پس از 12 سال، ما (12 + 12/4 ) وزارت دفاع 7 = 15 مد 7 = 1 . اگر y را با y mod 12 جایگزین کنیم ، این روز اضافی را دور می کنیم. اما با اضافه کردن تماس در ⌊ Y/12 ⌋ جبران برای این خطا، به فرمول نهایی.

روش "عجیب + 11" [ ویرایش ]

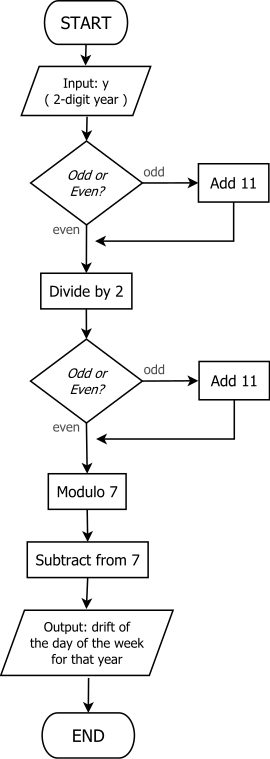
یک نمودار نمودار ساده که روش OD + 11 را نشان می دهد.

روش ساده ای برای پیدا کردن روز رستاخیز سال در سال 2010 توسط چمبرلین فونگ و مایکل K. والترز کشف شد ، [9] و در مقاله آنها ارسال شده به هفتمین کنگره بین المللی ریاضیات صنعتی و کاربردی (2011) شرح داده شده است. روش "عجیب + 11" نامیده می شود ، برای محاسبات معادل [9] است

\ سمت چپ (y + \ left \ lfloor \ frac {y} 4} \ Right \ rfloor \ Right) \ bmod 7.

از نظر محاسبات ذهنی بسیار مناسب است ، زیرا نیازی به تقسیم بر 4 یا 12 ندارد و به دلیل استفاده مکرر از آن از قانون "عجیب + 11" ، به راحتی می توان آن را به خاطر سپرد.

تمدید این روز برای رسیدن به روز رستاخیز ، این روش اغلب به عنوان جمع آوری یک T در حال اجرا در شش مرحله به شرح زیر توصیف می شود:

  1. بگذارید T دو رقم آخر سال باشد.
  2. اگر T عجیب است ، 11 را اضافه کنید.
  3. حالا بگذارید T = T/2 .
  4. اگر T عجیب است ، 11 را اضافه کنید.
  5. حالا اجازه دهید T = 7 - ( T mod 7) .
  6. تعداد رو به جلو T روز از روز لنگر قرن برای دریافت به روز قیامت به سال جاری است.

به عنوان مثال ، استفاده از این روش در سال 2005 ، مراحل زیر بیان می شود:

  1. T = 5
  2. T = 5 + 11 = 16 (اضافه کردن 11 به دلیل T عجیب است)
  3. T = 16/2 = 8
  4. T = 8 (از T حتیهیچ کاری نکنید)
  5. T = 7 - (8 مود 7) = 7 - 1 = 6
  6. روز رستاخیز برای 2005 = 6 + سه شنبه = دوشنبه

فرمول صریح روش عجیب و غریب 11:

{\ displaystyle 7- \ left [{\ frac {y + 11 (y \، {\ bmod {2}})} {2}} + 11 \ left ({\ frac {y + 11 (y \، {\ bmod {2}})} {2}} {\ bmod {2}} \ Right) \ Right] \ bmod {7}}.

اگرچه این عبارت بسیار دلهره آور و پیچیده به نظر می رسد ، در واقع ساده است [9] به دلیل یک زیر بیان مشترک y + 11 ( y mod 2)/2 که فقط باید یک بار محاسبه شود.