ریاضیات

آمار
طرح کلی آمارشناسان واژه نامه نشانه گذاری مجلات لیست موضوعات مقالات  پورتال ریاضی دسته بندی
v تی ه

توزیع نرمال ، بسیار معمول چگالی احتمال ، چون مفید از قضیه حد مرکزی .

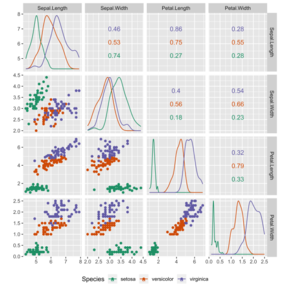
توطئه های پراکندگی در آمار توصیفی برای نشان دادن روابط مشاهده شده بین متغیرهای مختلف استفاده می شود ، در اینجا با استفاده از مجموعه داده های گل آیریس .

آمار رشته ای است که مربوط به جمع آوری ، سازماندهی ، تجزیه و تحلیل ، تفسیر و ارائه داده ها است. [1] [2] [3] در استفاده از آمار برای یک مشکل علمی ، صنعتی یا اجتماعی ، معمولی است که با یک جمعیت آماری یا یک مدل آماری که مورد بررسی قرار می گیرد ، شروع شود. جمعیت می تواند گروههای متنوعی از افراد یا اشیاء مانند "همه افرادی که در یک کشور زندگی می کنند" یا "هر اتمی که بلور را تشکیل می دهد" باشد. آمار به هر جنبه ای از داده ها ، از جمله برنامه ریزی برای جمع آوری داده ها از نظر طراحی نظرسنجی ها و آزمایش ها می پردازد. [4] به واژه نامه احتمالات و آمار مراجعه کنید .

هنگامی که داده های سرشماری را نمی توان جمع آوری کرد ، آمارشناسان با تهیه طرح های آزمایشی خاص و نمونه های پیمایشی داده ها را جمع آوری می کنند . نمونه گیری نماینده اطمینان می دهد که استنباط ها و نتیجه گیری می تواند به طور معقول از نمونه به کل جامعه گسترش یابد. یک مطالعه تجربی شامل اندازه گیری سیستم مورد بررسی ، دستکاری در سیستم و سپس انجام اندازه گیری های اضافی با استفاده از همین روش برای تعیین اینکه آیا این دستکاری مقادیر اندازه گیری ها را تغییر داده است یا خیر. در مقابل ، یک مطالعه مشاهده ای دستکاری آزمایشی را شامل نمی شود.

دو روش آماری اصلی در تجزیه و تحلیل داده ها به کار می رود : آمار توصیفی ، که خلاصه داده ها از یک نمونه با استفاده از شاخص هایی مانند میانگین یا انحراف استاندارد و آمار استنباطی است که نتیجه گیری از داده هایی که در معرض تغییر تصادفی هستند (به عنوان مثال ، خطاهای مشاهده ، تغییر نمونه) [5] آمار توصیفی اغلب به دو مجموعه از خصوصیات توزیع (نمونه یا جمعیت) مربوط می شود: تمایل اصلی (یا موقعیت مکانی ) به دنبال توصیف مقدار اصلی یا معمولی توزیع است ، در حالی که پراکندگی (یاتغییرپذیری ) میزان توزیع اعضای توزیع از مرکز آن و یکدیگر را مشخص می کند. استنباط در آمار ریاضی در چارچوب نظریه احتمال انجام می شود ، که به تجزیه و تحلیل پدیده های تصادفی می پردازد.

یک روش آماری استاندارد شامل آزمایش رابطه بین دو مجموعه داده آماری یا مجموعه داده ها و داده های مصنوعی است که از یک مدل ایده آل تهیه شده است. فرضیه ای برای رابطه آماری بین دو مجموعه داده ارائه شده است ، و این به عنوان جایگزینی برای یک فرضیه تهی ایده آل از هیچ ارتباطی بین دو مجموعه داده مقایسه می شود. رد یا عدم پذیرش فرضیه تهی با استفاده از تستهای آماری انجام می شود که با توجه به داده هایی که در این آزمون استفاده می شود ، می توان حس اثبات غلط بودن را اثبات کرد. با استفاده از یک فرضیه تهی ، دو اشکال اساسی خطا تشخیص داده می شود: خطاهای نوع I (فرضیه تهی به طور دروغی با دادن "مثبت کاذب" رد می شود) و خطاهای نوع II(فرضیه تهی رد نمی شود و رابطه واقعی بین جمعیت از دست دادن دادن "منفی کاذب" از دست می رود). [6] مشکلات چندگانه با این چهارچوب همراه است: اعم از اندازه کافی نمونه تا مشخص کردن یک فرضیه تهی کافی. [ نیاز به استناد ]

فرآیندهای اندازه گیری تولید داده های آماری نیز در معرض خطا هستند. بسیاری از این خطاها به صورت تصادفی (نویز) یا سیستماتیک ( تعصب ) طبقه بندی می شوند ، اما انواع دیگر خطاها (مانند اشتباه ، مانند وقتی که یک تحلیلگر واحد نادرست را گزارش می دهد) نیز می تواند رخ دهد. وجود داده های مفقود شده یا سانسور ممکن است منجر به تخمین های مغرضانه شود و تکنیک های خاصی برای رفع این مشکلات ایجاد شده است.

اولین مقاله ها در مورد احتمال و آمار ، روش های آماری که از تئوری احتمال گرفته شده اند ، مربوط به ریاضیدانان و رمزنگاران عرب است ، به ویژه آل خلیل (717-786) [7] و الکندی (801-873). [8] [9] در قرن 18th ، آمار نیز شروع به جلب توجه شدید از حساب کرد . در سالهای اخیر ، آمارها بیشتر به نرم افزارهای آماری متکی بوده اند تا بتوانند از این تست ها مانند تجزیه و تحلیل توصیفی استفاده کنند. [10]

فهرست

• 1مقدمه
  • 1.1آمار ریاضی
• 2تاریخچه
• 3داده های آماری
  • 3.1جمع آوری داده ها
  • 3.2انواع داده ها
• 4روش آماری
  • 4.1آمار توصیفی
  • 4.2آمار استنباطی
  • 4.3تجزیه و تحلیل داده های اکتشافی
• 5سوء استفاده
  • 5.1تفسیر نادرست: همبستگی
• 6برنامه کاربردی
  • 6.1آمار کاربردی ، آمار نظری و آمار ریاضی
  • 6.2یادگیری ماشین و داده کاوی
  • 6.3آمار در جامعه
  • 6.4محاسبه آماری
  • 6.5آمار مربوط به ریاضیات یا هنرهاست
• 7رشته تخصصی
• 8همچنین ببینید
• 9مرجع
• 10مطالعه بیشتر
• 11پیوند خارجی

مقدمه [ ویرایش ]

مقاله اصلی: خلاصه آمار

آمار یک بدنه ریاضی از علم است که به جمع آوری ، تحلیل ، تفسیر یا توضیح و ارائه داده ها ، [11] یا به عنوان شاخه ای از ریاضیات مربوط می شود . [12] بعضی ها آمار را یک علم ریاضی مجزا می دانند تا یک شاخه از ریاضیات. در حالی که بسیاری از تحقیقات علمی از داده ها استفاده می کنند ، آمار مربوط به استفاده از داده ها در زمینه عدم اطمینان و تصمیم گیری در مواجهه با عدم اطمینان است. [13] [14]

در استفاده از آمار برای یک مشکل ، معمول است که با یک جمعیت یا فرایندی که مورد مطالعه قرار می گیرد ، شروع شود. جمعیت ها می توانند موضوعات متنوعی مانند "همه افراد ساکن در یک کشور" یا "هر اتمی که بلور را تشکیل می دهد" باشد. در حالت ایده آل ، آمارشناسان اطلاعات مربوط به کل جمعیت (عملیاتی به نام سرشماری ) را گردآوری می کنند . این ممکن است توسط مؤسسات آماری دولتی سازماندهی شود. می توان از آمار توصیفی برای جمع بندی داده های جمعیت استفاده کرد. توصیف کنندگان عددی شامل میانگین و انحراف استاندارد برای انواع داده های مداوم (مانند درآمد) هستند ، در حالی که فراوانی و درصد از نظر توصیف داده های دسته ای (مانند آموزش) مفیدتر هستند .

هنگامی که سرشماری امکان پذیر نیست ، یک زیر مجموعه انتخاب شده از جمعیت به نام نمونه مورد مطالعه قرار می گیرد. هنگامی که نمونه ای که نماینده جمعیت باشد مشخص می شود ، داده ها برای اعضای نمونه در یک محیط مشاهده یا تجربی جمع آوری می شود. باز هم می توان از آمار توصیفی برای جمع بندی داده های نمونه استفاده کرد. اما ، ترسیم نمونه مورد عنصر تصادفی قرار گرفته است ، از این رو توصیفهای عددی تعیین شده از نمونه نیز به دلیل عدم اطمینان است. آمار استنباطی هنوز نتیجه گیری معنی دار در مورد کل جمعیت ، استنباط می شودلازم است. این از الگوهای موجود در داده های نمونه برای جلب استنباط در مورد جمعیت ارائه شده استفاده می کند و تصادفی بودن آن را تشکیل می دهد. این استنتاج ها ممکن است به صورت زیر باشد: پاسخ دادن به سؤالات بله / خیر در مورد داده ها ( آزمایش فرضیه ) ، برآورد ویژگی های عددی داده ها ( برآورد ) ، توصیف ارتباطات درون داده ها ( همبستگی ) و مدل سازی روابط درون داده ها (مثلاً استفاده از تحلیل رگرسیون ). استنتاج می تواند به پیش بینی ، پیش بینی و تخمین مقادیر غیرقابل محافظت یا با جمعیت مورد مطالعه در ارتباط باشد یا گسترش یابد . این می تواند شامل برون یابی و درون یابی باشداز سری های زمانی و یا داده های فضایی ، و همچنین می تواند شامل داده کاوی .

آمار ریاضی [ ویرایش ]

مقاله اصلی: آمار ریاضی

آمار ریاضی کاربرد ریاضیات به آمار است. تکنیک های ریاضی مورد استفاده برای این شامل تجزیه و تحلیل ریاضی ، جبر خطی ، آنالیز تصادفی ، معادلات دیفرانسیل و نظریه احتمال اندازه گیری- نظری است . [15] [16]

تاریخچه [ ویرایش ]

Gerolamo Cardano ، پیشگام ریاضیات احتمال است.

مقالات اصلی: تاریخچه آمار و بنیانگذاران آمار

نخستین نوشته ها در مورد احتمال و آمار مربوط به ریاضیدانان و رمزنگاران عرب است ، در دوره طلایی اسلامی بین قرن هشتم و سیزدهم. آل خلیل (717-786) کتاب پیام های رمزنگاری را که شامل اولین استفاده از ترکیب ها و ترکیب ها است ، نوشت تا تمام کلمات عربی ممکن را با و بدون مصوت ها فهرست کند. [7] اولین کتاب در زمینه آمار ، نسخه خطی رساله قرن نهم در کشف رمزنگاری پیام های رمزنگاری است ، که توسط محقق عرب الکندی نوشته شده است(801-873). الكندی در كتاب خود شرح مفصلی در مورد چگونگی استفاده از آمار و تحلیل فراوانی برای رمزگشایی پیام های رمزگذاری شده ارائه داد . این متن پایه و اساس آمار و رمزنگاری را پایه گذاری کرده است . [8] [9] همچنین ال كندی نخستین استفاده از استنباط آماری را به دست آورد ، در حالی كه او و بعدا رمزنگاران عرب روشهای آماری اولیه را برای رمزگشایی پیام های رمزگذاری شده ایجاد كردند. ابن عدلان (1187 - 1168) بعداً در استفاده از اندازه نمونه در تجزیه و تحلیل فرکانس نقش مهمی را ایفا کرد . [7]

نخستین مقاله در مورد آمار اروپا به سال 1663 باز می گردد ، با انتشار مشاهدات طبیعی و سیاسی درباره لوایح مرگ و میر توسط جان گروت . [17] برنامه های اولیه تفکر آماری حول نیاز کشورها برای پایه گذاری سیاست های دموگرافیک و اقتصادی ، از این رو آمارشناسی آن تغییر یافته است . دامنه رشته آمار در اوایل قرن نوزدهم گسترش یافته است تا شامل جمع آوری و تجزیه و تحلیل داده ها بطور کلی باشد. امروز ، آمار به طور گسترده در دولت ، تجارت و علوم طبیعی و اجتماعی به کار می رود.

مبانی ریاضیات آمارهای مدرن در قرن 17 با توسعه تئوری احتمال توسط Gerolamo Cardano ، Blaise Pascal و Pierre Fermat گذاشته شد . نظریه احتمال ریاضی ناشی از مطالعه بازی های شانس است ، اگرچه مفهوم احتمال قبلاً در قانون قرون وسطایی و توسط فیلسوفانی چون خوان کاراموئل مورد بررسی قرار گرفته است . [18] روش حداقل مربعات برای اولین بار توسط توصیف شد آدرین-ماری لژاندر در 1805.

کارل پیرسون ، بنیانگذار آمار ریاضی.

زمینه مدرن آمار در اواخر قرن نوزدهم و اوایل قرن بیستم در سه مرحله پدید آمده است. [19] موج اول ، در اواخر قرن ، با کار فرانسیس گالتون و کارل پیرسون انجام شد ، که آمار را به یک رشته ریاضی سختگیرانه تبدیل می کردند که برای تجزیه و تحلیل استفاده می شد ، نه فقط در علم ، بلکه در صنعت و سیاست نیز. . مشارکتهای گالتون شامل معرفی مفاهیم انحراف استاندارد ، همبستگی ، تحلیل رگرسیون و کاربرد این روشها در بررسی انواع ویژگیهای انسانی قد ، وزن ، طول مژه در بین دیگران است. [20] پیرسون توسعهضریب همبستگی پیرسون گشتاوری ، تعریف به عنوان یک محصول-لحظه، [21] روش گشتاورها برای اتصالات از توزیع به نمونه و توزیع پیرسون ، در میان بسیاری چیزهای دیگر. [22] گالتون و پیرسون Biometrika را به عنوان اولین ژورنال آمار ریاضی و زیست آمار (که پس از آن بیومتری خوانده می شد) تأسیس کردند ، و دومی اولین بخش آمار دانشگاه جهان را در کالج دانشگاه لندن تأسیس کرد . [23]

رونالد فیشر اصطلاح فرضیه تهی را در طول آزمایش چای مزه چینی ابداع كرد ، كه "هرگز اثبات و یا اثبات نشده ، اما احتمالاً در جریان آزمایش رد شده است". [24] [25]

موج دوم دهه 1910 و 20 توسط ویلیام سیالی گاست آغاز شد و در بینش رونالد فیشر که کتابهای درسی را برای تعریف رشته دانشگاهی در دانشگاه های سراسر جهان نوشت ، به اوج خود رسید . مهمترین نشریات فیشر مقاله اصلی او در سال 1918 با عنوان "همبستگی بین اقوام با فرض مندلیان وراثت بود (که اولین نفری بود که از اصطلاح آماری ، واریانس استفاده کرد ) ، کار کلاسیک وی در سال 1925 روشهای آماری برای کارگران تحقیق و 1935 او با طراحی آزمایشها ، [26] [27] [28] جایی که او طراحی دقیق آزمایش را انجام دادمدل ها. او سرچشمه مفاهیم کفایت ، آمار کمکی ، تبعیض آمیز خطی فیشر و اطلاعات فیشر بود . [29] در کتاب خود در سال 1930 نظریه ژنتیکی انتخاب طبیعی ، او از آماری برای مفاهیم مختلف بیولوژیکی مانند اصل فیشر [30] استفاده کرد (که AWF ادواردز آن را "احتمالاً مشهورترین برهان در زیست شناسی تکاملی " نامید) و فراری فیشر ، [31] ] [32] [33] [34] [35] [36] یک مفهوم درانتخاب جنسی در مورد تأثیر مثبت فراری بازخورد که در تکامل دیده می شود .

موج نهایی ، که عمدتاً از پالایش و گسترش تحولات قبلی دیده می شد ، ناشی از همکاری مشترک بین اگون پیرسون و جرزی نیممن در دهه 1930 بود. آنها مفاهیم خطای " نوع دوم " ، قدرت آزمایش و فواصل اطمینان را معرفی کردند . جرزی نایمن در سال 1934 نشان داد که نمونه گیری تصادفی طبقه ای به طور کلی روش بهتری برای تخمین از نمونه گیری هدفمند (سهمیه) است. [37]

امروزه از روشهای آماری در کلیه زمینه هایی که شامل تصمیم گیری است ، برای انجام استنباط دقیق از مجموعه داده های جمع آوری شده و تصمیم گیری در مواجهه با عدم اطمینان براساس روش آماری استفاده می شود. استفاده از رایانه های مدرن باعث تسریع در محاسبات آماری در مقیاس بزرگ شده و همچنین روشهای جدیدی را امکان پذیر ساخته است که عملی نیستند. آمار همچنان منطقه ای از تحقیقات فعال به عنوان مثال در مورد مسئله چگونگی تجزیه و تحلیل داده های بزرگ است . [38]

منبع

https://en.wikipedia.org/wiki/Statistics