مقالاتی در مورد
الکترومغناطیس
سلونوئید

این مقاله معادلات در نظریه الکترومغناطیس را خلاصه می‌کند .

تعاریف

[ ویرایش ]

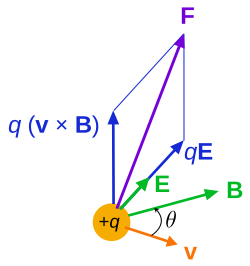
نیروی لورنتس وارد بر یک ذره باردار (با بار q ) در حال حرکت (سرعت v )، که به عنوان تعریف میدان E و میدان B استفاده می‌شود .

در اینجا از اندیس‌های e و m برای تمایز بین بارهای الکتریکی و مغناطیسی استفاده می‌شود . تعاریف تک‌قطبی‌ها از نظر تئوری مورد توجه هستند، اگرچه دوقطبی‌های مغناطیسی واقعی را می‌توان با استفاده از قدرت قطب‌ها توصیف کرد. دو واحد ممکن برای قدرت تک‌قطبی وجود دارد، Wb (وبر) و A m (آمپر متر). تجزیه و تحلیل ابعادی نشان می‌دهد که بارهای مغناطیسی با q m (Wb) = μ 0 q m (Am) مرتبط هستند.

مقادیر اولیه

[ ویرایش ]

تعداد (نام/نام‌های رایج)نماد/نمادهای (رایج)واحدهای SIابعاد
بار الکتریکیq e ، q ، QC = همانطور که[من][تی]
قدرت تک‌قطبی ، بار مغناطیسیq متر ، g ، pWb یا Am[L] 2 [M][T] −2 [I] −1 (Wb)

[من][ل] (هستم)

کمیت‌های الکتریکی

[ ویرایش ]

توزیع پیوسته بار. چگالی بار حجمی ρ مقدار بار در واحد حجم (مکعب)، چگالی بار سطحی σ مقدار بار در واحد سطح (دایره) با عمود بر واحد بیرونی n̂ ، d گشتاور دوقطبی بین دو بار نقطه‌ای است ، چگالی حجمی اینها چگالی قطبش P است . بردار موقعیت r نقطه‌ای برای محاسبه میدان الکتریکی است؛ r′ نقطه‌ای در جسم باردار است.

برخلاف قیاس قوی بین گرانش (کلاسیک) و الکترواستاتیک ، هیچ «مرکز بار» یا «مرکز جاذبه الکترواستاتیکی» مشابهی وجود ندارد. [ نیازمند منبع ]

حمل و نقل الکتریکی

تعداد (نام/نام‌های رایج)نماد/نمادهای (رایج)تعریف معادلهواحدهای SIابعاد
چگالی بار خطی، سطحی و حجمیλ e برای خطی، σ e برای سطح، ρ e برای حجم.{\displaystyle q_{e}=\int \lambda _{e}\mathrm {d} \ell }

{\displaystyle q_{e}=\iint \sigma _{e}\mathrm {d} S}

{\displaystyle q_{e}=\iiint \rho _{e}\mathrm {d} V}

C m − n ، n = 1، 2، 3[I][T][L] − n
ظرفیتC{\displaystyle C={\mathrm {d} q \over \mathrm {d} V}\,\!}

V = ولتاژ، نه حجم.

F = CV −1[اول] ۲ [ت] ۴ [ل] −۲ [م] −۱
جریان الکتریکیI\displaystyle I={\mathrm {d} q \over \mathrm {d} t}\,\!}A[I]
چگالی جریان الکتریکیجی{\displaystyle I=\mathbf {J} \cdot \mathrm {d} \mathbf {S} }یک متر مربع (A m −2)[اول][ل] −۲
چگالی جریان جابجاییجی دی\displaystyle \mathbf {J} _{\mathrm {d} }={\partial \mathbf {D} \over \partial t}=\varepsilon _{0}\left({\partial \mathbf {E} \over \partial t}\right)\,\!}یک متر مربع (A m −2)[اول][ل] −۲
چگالی جریان همرفتیجی سی{\displaystyle \mathbf {J} _{\mathrm {c} }=\rho \mathbf {v} \,\!}یک متر مربع (A m −2)[اول][ل] −۲