از ویکیپدیا، دانشنامه آزاد

در فیزیک و شیمی، عدد کوانتومی اسپین یک عدد کوانتومی ( s تعیین شده) است که تکانه زاویه ای ذاتی (یا تکانه زاویه ای اسپین یا به سادگی اسپین ) یک الکترون یا ذره دیگر را توصیف می کند . این مقدار برای همه ذرات یک نوع مانند s = یکسان است1/2برای همه الکترون ها این یک عدد صحیح برای همه بوزون ها مانند فوتون ها و یک عدد نیمه فرد صحیح برای همه فرمیون ها مانند الکترون ها و پروتون ها است .

جزء اسپین در امتداد یک محور مشخص شده توسط عدد کوانتومی مغناطیسی اسپین که به طور معمول m s نوشته می شود، به دست می آید . [1] [2] مقدار m s جزء تکانه زاویه‌ای اسپین است، بر حسب واحد کاهش ثابت پلانک ħ ، موازی با یک جهت معین (که معمولاً محور z نامگذاری می‌شود ). می تواند مقادیری از + s تا - s را در افزایش عدد صحیح بگیرد. برای یک الکترون، m s می تواند + باشد+1/2یا -+1/2.

نامگذاری [ ویرایش ]

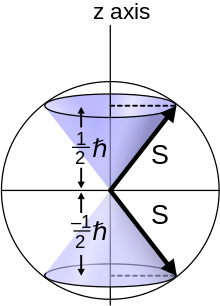
طرح ریزی کوانتومی S به z برای نیم ذرات اسپین

عبارت عدد کوانتومی اسپین به تکانه زاویه ای اسپین کوانتیزه شده اشاره دارد . نماد s برای عدد کوانتومی اسپین استفاده می شود و m s به عنوان عدد کوانتومی مغناطیسی اسپین [3] یا به عنوان مولفه z اسپین s z توصیف می شود . [4]

هم اسپین کل و هم مولفه z اسپین کوانتیزه می شوند که منجر به دو عدد کوانتومی اسپین و آهنربای اسپین می شود. [5] عدد کوانتومی اسپین (کل) تنها یک مقدار برای هر ذره بنیادی دارد. برخی از کتب مقدماتی شیمی، m s را به عنوان عدد کوانتومی اسپین توصیف می کنند ، [6] [7] و s به دلیل مقدار آن ذکر نشده است.1/2خاصیت ثابت الکترون است. برخی حتی از متغیر s به جای m s استفاده می کنند . [5]

دو عدد کوانتومی اسپینی {\displaystyle s}و{\displaystyle m_{s}}آنالوگ‌های تکانه زاویه‌ای چرخشی دو عدد کوانتومی تکانه زاویه‌ای مداری هستند {\displaystyle l}و{\displaystyle m_{l}}. [8] : 152 

اعداد کوانتومی اسپین برای سیستم های اسپین های جفت شده، مانند اتم هایی که ممکن است بیش از یک الکترون داشته باشند، نیز کاربرد دارند. نمادهای با حروف بزرگ استفاده می شود: S برای کل چرخش الکترونیکی، و m S یا M S برای جزء z -axis. یک جفت الکترون در حالت منفرد اسپین دارای S = 0، و یک جفت در حالت سه گانه دارای S = 1، با mS = -1، 0 یا +1 است. اعداد کوانتومی اسپین هسته ای به طور متعارف I برای اسپین و m I یا M I برای مولفه z -axis نوشته می شوند.

نام "اسپین" از چرخش هندسی الکترون حول یک محور گرفته شده است، همانطور که توسط Uhlenbeck و Goudsmit پیشنهاد شده است . با این حال، این تصویر ساده به سرعت متوجه شد که از نظر فیزیکی غیرواقعی است، زیرا نیاز به چرخش الکترون‌ها سریع‌تر از سرعت نور دارد. [9] بنابراین با توصیف مکانیکی کوانتومی انتزاعی تر جایگزین شد.

تاریخچه [ ویرایش ]

همچنین ببینید: اسپین (فیزیک) § تاریخ

در طول دوره بین 1916 و 1925، پیشرفت های زیادی در مورد آرایش الکترون ها در جدول تناوبی انجام شد . به منظور توضیح اثر زیمن در اتم بور، سامرفلد پیشنهاد کرد که الکترون‌ها بر اساس سه عدد کوانتومی، n، k و m هستند که اندازه مدار، شکل مدار و جهت را توصیف می‌کنند. که مدار در آن اشاره می کرد. [10] ایروینگ لانگمویر در مقاله خود در سال 1919 در مورد الکترون ها در پوسته آنها توضیح داده بود، "ریدبرگ اشاره کرده است که این اعداد از سری به دست آمده اند{\displaystyle N=2(1+2^{2}+2^{2}+3^{2}+3^{2}+4^{2})}. عامل دو یک تقارن دو برابری اساسی را برای همه اتم‌های پایدار نشان می‌دهد.» [11] این{\displaystyle 2n^{2}}این پیکربندی توسط ادموند استونر در اکتبر 1924 در مقاله‌اش «توزیع الکترون‌ها در میان سطوح اتمی» که در مجله فیلسوفیک منتشر شد، پذیرفته شد .

موفقیت کیفی طرح اعداد کوانتومی سامرفلد در توضیح اثر زیمن در قدرت میدان مغناطیسی ضعیف، اثر غیرعادی زیمن، شکست خورد . در دسامبر 1924، ولفگانگ پائولی نشان داد که تکانه زاویه ای الکترون هسته با اثری که قبلاً فرض شده بود، ارتباطی ندارد. [12] : 563  در عوض او پیشنهاد کرد که فقط الکترون های "نور" بیرونی تکانه زاویه ای را تعیین می کنند و او فرض کرد که این به یک عدد کوانتومی چهارم با دو مقدار نیاز دارد. [13] این چهارمین عدد کوانتومی به عدد کوانتومی مغناطیسی اسپین تبدیل شد.

اسپین الکترون [ ویرایش ]

نوشتار اصلی: اسپین (فیزیک)

یک چرخش

- 1 /2

ذره با یک عدد کوانتومی تکانه زاویه ای برای اسپین s = مشخص می شود

 1 /2.

در حل معادله شرودینگر-پائولی ، تکانه زاویه ای بر اساس این عدد کوانتیزه می شود، به طوری که بزرگی تکانه زاویه ای اسپینی برابر است با

{\displaystyle \|{\mathbf {S}}\|=\hbar {\sqrt {s(s+1)}}={\tfrac {\sqrt {3}}{2}}\ \hbar ~.}

ساختار ظریف طیف هیدروژن به صورت یک دوتایی مشاهده می شود که مربوط به دو احتمال برای مولفه z تکانه زاویه ای است، که در آن برای هر جهت معین z :

{\displaystyle s_{z}=\pm {\tfrac {1}{2}}\hbar ~.}

که حل آن فقط دو مولفه z ممکن برای الکترون دارد. در الکترون، دو جهت اسپین مختلف، گاهی اوقات «اسپین به بالا» یا «اسپین پایین» نامیده می‌شوند.

خاصیت اسپینی یک الکترون باعث ایجاد گشتاور مغناطیسی می شود که لازمه چهارمین عدد کوانتومی بود.

بردار گشتاور مغناطیسی یک اسپین الکترون به صورت زیر بدست می آید:

{\displaystyle \ {\boldsymbol {\mu }}_{\text{s}}=-{\frac {e}{\ 2m\ }}\ g_{\text{s}}\ {\mathbf {S} }\ }

جایی که{\displaystyle -e}بار الکترون است ،{\displaystyle m}جرم الکترون است و{\displaystyle g_{\text{s}}}ضریب g اسپین الکترون است که تقریباً 2.0023 است. طرح ریزی محور z آن توسط عدد کوانتومی مغناطیسی اسپینی به دست می آید{\displaystyle m_{\text{s}}}مطابق با:

{\displaystyle \mu _{z}=-m_{\text{s}}\ g_{\text{s}}\ \mu _{\mathsf {B}}=\pm {\tfrac {1}{2 }}\ g_{\text{s}}\ \mu _{\mathsf {B}}\ }

جایی که {\displaystyle \ \mu _{\mathsf {B}}\ }مگنتون بور است .

وقتی اتم ها دارای تعداد زوج الکترون باشند، اسپین هر الکترون در هر اوربیتال جهت گیری مخالف همسایه(های) بلافصل خود دارد. با این حال، بسیاری از اتم‌ها دارای تعداد فرد الکترون یا آرایش الکترون‌هایی هستند که در آن تعداد جهت‌گیری «اسپین به بالا» و «اسپین به پایین» نامساوی است. گفته می شود که این اتم ها یا الکترون ها دارای اسپین های جفت نشده ای هستند که در رزونانس اسپین الکترون شناسایی می شوند .

اسپین هسته ای [ ویرایش ]

هسته های اتمی نیز دارای اسپین هستند. اسپین هسته ای I یک ویژگی ثابت هر هسته است و ممکن است یک عدد صحیح یا یک عدد نیمه صحیح باشد. مولفه m I اسپین هسته ای موازی با محور z می تواند مقادیر (2 I + 1) I , I –1, ..., –I داشته باشد . به عنوان مثال، یک هسته 14 N دارای I = 1 است، به طوری که 3 جهت ممکن نسبت به محور z وجود دارد که مربوط به حالات mI = +1، 0 و -1 است. [14]

اسپین های I هسته های مختلف با استفاده از مدل پوسته هسته ای تفسیر می شوند . هسته‌های زوج با تعداد پروتون‌ها و نوترون‌های زوج، مانند 12 C و 16 O ، دارای اسپین صفر هستند. هسته های عدد جرمی فرد دارای اسپین های نیمه صحیح هستند، مانند3/ 2 برای 7 لی ، 1 /2برای 13 درجه سانتیگراد و5/ 2 برای 17 O ، معمولاً مربوط به تکانه زاویه ای آخرین نوکلئون اضافه شده است. هسته های فرد و فرد با اعداد فرد پروتون و نوترون دارای اسپین های صحیح هستند ، مانند 3 برای 10 B و 1 برای 14 N. [15] مقادیر اسپین هسته ای برای یک ایزوتوپ معین در فهرست ایزوتوپ ها برای هر عنصر یافت می شود. (به ایزوتوپ های اکسیژن ، ایزوتوپ های آلومینیوم و غیره و غیره مراجعه کنید)

تشخیص چرخش [ ویرایش ]

هنگامی که خطوط طیف هیدروژن با وضوح بسیار بالا مورد بررسی قرار می گیرند، مشخص می شود که آنها دوتایی با فاصله نزدیک هستند. این شکاف ساختار ظریف نامیده می شود و یکی از اولین شواهد تجربی برای اسپین الکترون بود. مشاهده مستقیم تکانه زاویه ای ذاتی الکترون در آزمایش استرن-گرلاخ به دست آمد .

آزمایش استرن-گرلاخ [ ویرایش ]

مقاله اصلی: آزمایش استرن-گرلاخ

نظریه کوانتیزاسیون فضایی گشتاور اسپین تکانه الکترونهای اتمهای واقع در میدان مغناطیسی نیاز به اثبات تجربی داشت. در سال 1922 (دو سال قبل از اینکه توصیف نظری اسپین ایجاد شود) اتو استرن و والتر گرلاخ در آزمایشی که انجام دادند آن را مشاهده کردند.

اتم های نقره با استفاده از یک کوره الکتریکی در خلاء تبخیر شدند. با استفاده از شکاف‌های نازک، اتم‌ها به یک پرتو مسطح هدایت شدند و پرتو قبل از برخورد با یک صفحه فلزی از طریق یک میدان مغناطیسی همگن فرستاده شد. قوانین فیزیک کلاسیک پیش بینی می کند که مجموعه اتم های نقره متراکم روی صفحه باید یک خط جامد نازک به شکل پرتو اصلی تشکیل دهد. با این حال، میدان مغناطیسی همگن باعث شد پرتو در دو جهت جداگانه تقسیم شود و دو خط روی صفحه فلزی ایجاد شود.

این پدیده را می توان با کوانتیزه فضایی گشتاور اسپین تکانه توضیح داد. در اتم ها، الکترون ها به گونه ای جفت می شوند که یکی به سمت بالا و دیگری به سمت پایین می چرخد ​​و تأثیر اسپین آنها بر عملکرد اتم به عنوان یک کل خنثی می شود. اما در لایه ظرفیت اتم‌های نقره، یک الکترون وجود دارد که اسپین آن نامتعادل باقی می‌ماند.

اسپین نامتعادل گشتاور مغناطیسی اسپینی ایجاد می کند و باعث می شود الکترون مانند یک آهنربای بسیار کوچک عمل کند. همانطور که اتم ها از میدان مغناطیسی همگن عبور می کنند، گشتاور نیرو در میدان مغناطیسی بر دوقطبی الکترون تأثیر می گذارد تا جایی که موقعیت آن با جهت میدان قوی تر مطابقت داشته باشد. سپس اتم بسته به مقدار اسپین الکترون ظرفیت، مقدار مشخصی به سمت میدان مغناطیسی قوی‌تر یا دور از آن کشیده می‌شود. وقتی اسپین الکترون + باشد+ 1 /2اتم از میدان قوی‌تر دور می‌شود و وقتی اسپین − است+ 1 /2اتم به سمت آن حرکت می کند. بنابراین، پرتو اتم‌های نقره در حین حرکت در میدان مغناطیسی همگن، بر اساس اسپین الکترون ظرفیت هر اتم، شکافته می‌شود.

در سال 1927 فیپس و تیلور آزمایش مشابهی را با استفاده از اتم های هیدروژن با نتایج مشابه انجام دادند. بعداً دانشمندان آزمایشاتی را با استفاده از اتم های دیگری که فقط یک الکترون در لایه ظرفیت خود دارند انجام دادند: ( مس ، طلا ، سدیم ، پتاسیم ). هر بار دو خط روی صفحه فلزی تشکیل می شد.

هسته اتم نیز ممکن است دارای اسپین باشد، اما پروتون ها و نوترون ها بسیار سنگین تر از الکترون ها هستند (حدود 1836 برابر)، و گشتاور دوقطبی مغناطیسی با جرم نسبت عکس دارد. بنابراین تکانه دوقطبی مغناطیسی هسته ای بسیار کوچکتر از کل اتم است. این دوقطبی مغناطیسی کوچک بعدها توسط استرن، فریش و ایسترمن اندازه گیری شد.

رزونانس پارامغناطیسی الکترون [ ویرایش ]

برای اتم‌ها یا مولکول‌های دارای الکترون جفت نشده، انتقال‌هایی در یک میدان مغناطیسی نیز قابل مشاهده است که در آن فقط عدد کوانتومی اسپین تغییر می‌کند، بدون تغییر در اوربیتال الکترونی یا سایر اعداد کوانتومی. این روش رزونانس پارامغناطیس الکترون (EPR) یا رزونانس اسپین الکترون (ESR) است که برای مطالعه رادیکال‌های آزاد استفاده می‌شود . از آنجایی که فقط برهمکنش مغناطیسی اسپین تغییر می کند، تغییر انرژی بسیار کمتر از انتقال بین اوربیتال ها است و طیف ها در ناحیه مایکروویو مشاهده می شوند .

ارتباط با بردارهای اسپین [ ویرایش ]

برای حل معادله پاولی غیرنسبیتی یا معادله دیراک نسبیتی ، تکانه زاویه ای کوانتیزه شده (به عدد کوانتومی تکانه زاویه ای مراجعه کنید ) را می توان به صورت زیر نوشت:

{\displaystyle \Vert \mathbf {s} \Vert ={\sqrt {s\,(s+1)\,}}\,\hbar }

جایی که

با توجه به جهت دلخواه z (معمولاً توسط یک میدان مغناطیسی خارجی تعیین می شود) spin z -projection توسط

{\displaystyle s_{z}=m_{s}\,\hbar }

که در آن m s عدد کوانتومی اسپین مغناطیسی است که از −s تا + s در مراحل یک متغیر است. این 2  s + 1 مقدار متفاوت m s ایجاد می کند .

مقادیر مجاز برای s اعداد صحیح غیر منفی یا اعداد نیمه صحیح هستند . فرمیون ها دارای مقادیر نیمه صحیح هستند، از جمله الکترون ، پروتون و نوترون که همگی دارای s = + هستند. + 1 /2. بوزون هایی مانند فوتون و همه مزون ها دارای مقادیر اسپین عدد صحیح هستند.

جبر [ ویرایش ]

نظریه جبری اسپین کپی کربنی از تکانه زاویه ای در نظریه مکانیک کوانتومی است . [16] اول از همه، اسپین رابطه کموتاسیون اساسی را برآورده می کند :

{\displaystyle \ [S_{i},S_{j}]=i\ \hbar \\epsilon _{ijk}\ S_{k}\ ,}

{\displaystyle \ \left[S_{i},S^{2}\right]=0\ }جایی که {\displaystyle \ \epsilon _{ijk}\ }نماد (ضد متقارن) Levi-Civita است . این بدان معنی است که به دلیل محدودیت اصل عدم قطعیت ، شناخت دو مختصات اسپین به طور همزمان غیرممکن است .

بعد، بردارهای ویژه از {\displaystyle \ S^{2}\ }و {\displaystyle \ S_{z}\ }ارضا کردن:

{\displaystyle \ S^{2}\ |s,m_{s}\rangle ={\hbar }^{2}\ s(s+1)\ |s,m_{s}\rangle \ }

{\displaystyle \ S_{z}\ |s,m_{s}\rangle =\hbar \ m_{s}\ |s,m_{s}\rangle \ }

{\displaystyle \ S_{\pm }\ |s,m_{s}\rangle =\hbar \ {\sqrt {s(s+1)-m_{s}(m_{s}\pm 1)\ }} \;|s,m_{s}\pm 1\rangle \ }

جایی که {\displaystyle \ S_{\pm }=S_{x}\pm iS_{y}\ }عملگرهای نردبانی (یا "بالا بردن" و "پایین آوردن") هستند .

سطوح انرژی از معادله دیراک [ ویرایش ]

در سال 1928، پل دیراک معادله موج نسبیتی را ایجاد کرد که اکنون معادله دیراک نامیده می شود ، که گشتاور مغناطیسی اسپین را به درستی پیش بینی می کرد و در همان زمان الکترون را به عنوان یک ذره نقطه مانند در نظر می گرفت. حل معادله دیراک برای سطوح انرژی یک الکترون در اتم هیدروژن، هر چهار عدد کوانتومی شامل s به طور طبیعی رخ داده و به خوبی با آزمایش مطابقت دارد.

اسپین کل یک اتم یا مولکول [ ویرایش ]

برای برخی از اتم ها، اسپین های چندین الکترون جفت نشده ( s 1 ، s 2 ، ...) با هم جفت می شوند تا یک عدد کوانتومی اسپین کل S را تشکیل دهند . [17] [18] این امر به ویژه در اتم‌های سبک (یا در مولکول‌هایی که فقط از اتم‌های سبک تشکیل شده‌اند) اتفاق می‌افتد، زمانی که جفت شدن مدار اسپین در مقایسه با جفت بین اسپین‌ها یا جفت شدن بین گشتاور زاویه‌ای مداری ضعیف است ، وضعیتی که به نام جفت شدن L S شناخته می‌شود . L و S ثابت حرکت هستند . در اینجا L کل عدد کوانتومی تکانه زاویه ای مداری است . [18]

برای اتم هایی با S به خوبی تعریف شده ، تعدد یک حالت به صورت 2 S + 1 تعریف می شود . این برابر است با تعداد مقادیر مختلف ممکن از کل (مدار به علاوه اسپین) تکانه زاویه ای J برای یک ترکیب معین ( L ، S )، مشروط بر اینکه S ≤ L (مورد معمولی). به عنوان مثال، اگر S = 1 باشد، سه حالت وجود دارد که یک سه گانه را تشکیل می دهند . مقادیر ویژه S z برای این سه حالت +1ħ، 0 و -1ħ هستند . [17] واژه نماد حالت اتمی مقادیر L ، S و J را نشان می دهد .

به عنوان مثال، حالت های پایه هر دو اتم اکسیژن و مولکول دی اکسیژن دارای دو الکترون جفت نشده هستند و بنابراین حالت های سه گانه هستند. حالت اتمی با عبارت نماد 3 P و حالت مولکولی با عبارت نماد 3 Σ توصیف می شود-
g.

همچنین ببینید [ ویرایش ]

منابع

https://en.wikipedia.org/wiki/Spin_quantum_number