3-کاردیوئید
خواص متریک [ ویرایش ]
برای کاردیوئید همانطور که در بالا تعریف شده است، فرمول های زیر وجود دارد:
- مساحت
،
- طول کمان
و
- شعاع انحنا .
شواهد این اظهارات در هر دو مورد از نمایش قطبی کاردیوئید استفاده می کنند. برای فرمول های مناسب به سیستم مختصات قطبی (طول قوس) و سیستم مختصات قطبی (مساحت) مراجعه کنید.
اثبات فرمول مساحت
اثبات فرمول طول قوس
اثبات شعاع انحنا
شعاع انحنا

برای کاردیوئید
.
خواص [ ویرایش ]
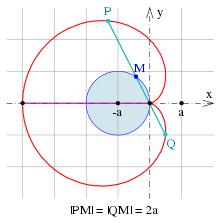
آکورد یک کاردیوئید
آکورد از طریق قله [ ویرایش ]
C1
آکوردهای از طریق کاسپ کاردیوئید طول یکسانی دارند
C2
نقاط میانی آکوردها از طریق کاسپ در محیط دایره مولد ثابت قرار دارند (تصویر را ببینید) .
اثبات C1 [ ویرایش ]
نقاط
اثبات برای C2 [ ویرایش ]
برای اثبات از نمایش در صفحه مختلط (به بالا مراجعه کنید) استفاده می شود. برای امتیازات

نقطه وسط آکوردپس



کاردیوئید به عنوان منحنی معکوس سهمی [ ویرایش ]

کاردیوئید تولید شده از وارونگی یک سهمی در سراسر دایره واحد (خطوط)
نوشتار اصلی: هندسه معکوس
کاردیوئید منحنی معکوس سهمی است که کانون آن در مرکز وارونگی است (نمودار را ببینید)
برای مثال نشان داده شده در نمودار، دایره های مولد دارای شعاع هستند



نکته: هر منحنی معکوس سهمی کاردیوئید نیست. به عنوان مثال، اگر سهمی در دایرهای که مرکز آن در راس سهمی قرار دارد معکوس شود ، نتیجه یک سیسوئید از Diocles است .
کاردیوئید به عنوان پاکت مداد دایره ای [ ویرایش ]

کاردیوئید به عنوان پاکت مداد دایره ای
در بخش قبل، اگر مماس های سهمی را معکوس کنیم، مدادی از دایره در مرکز وارونگی (منشا) به دست می آید. بررسی دقیق نشان می دهد: نقاط میانی دایره ها در محیط دایره مولد ثابت قرار دارند. (دایره مولد منحنی معکوس جهت سهمی است.)
این ویژگی باعث ایجاد روش ساده زیر برای کشیدن یک کاردیوئید می شود:
- یک دایره انتخاب کنید
و یک نکته
در محیط آن،
- رسم دایره های حاوی
با مراکز روی
، و
- پاکت این دایره ها را بکشید.
اثبات با شرایط پاکت
پاکت مداد منحنی های تلویحی داده شده






اجازه دهید











کاردیوئید به عنوان پاکت مداد خطوط [ ویرایش ]

کاردیوئید به عنوان پاکت یک مداد از خطوط
یک روش مشابه و ساده برای کشیدن کاردیوئید از یک مداد خطوط استفاده می کند . این به دلیل L. Cremona است :
- یک دایره بکشید، محیط آن را به قسمت های مساوی تقسیم کنید
نقاط (تصویر) و آنها را به طور متوالی شماره گذاری کنید.
- آکوردها را بکشید:
. (یعنی نقطه دوم با سرعت دو برابر حرکت می کند.)
- پاکت این آکوردها کاردیوئید است.

نسل کرمونا از یک کاردیوئید
اثبات [ ویرایش ]
در نظر زیر از فرمول های مثلثاتی استفاده می شود





معادله مماس کاردیوئید با نمایش قطبی r = 2 (1 + cos 𝜑 ) [ ویرایش ]
از نمایش پارامتریک
یکی بردار معمولی را دریافت می کند

با کمک فرمول های مثلثاتی و تقسیم بعدی بر
معادله وتر دایره با نقطه میانی ( 1, 0 ) و شعاع 3 [ ویرایش ]
برای معادله خط مقطعی که از دو نقطه می گذرد
با کمک فرمول های مثلثاتی و تقسیم بعدی بر



![{\displaystyle \rho (\varphi )={\frac {\left[r(\varphi )^{2}+{\dot {r}}(\varphi )^{2}\right]^{3/2 }}{r(\varphi )^{2}+2{\dot {r}}(\varphi )^{2}-r(\varphi ){\ddot {r}}(\varphi )}}\ . }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e7cf0dc8bbc7c290a5046d1002a3ad215646126)
![{\displaystyle \rho (\varphi )=\cdots ={\frac {\left[16a^{2}\sin ^{2}{\frac {\varphi }{2}}\right]^{\frac { 3}{2}}}{24a^{2}\sin ^{2}{\frac {\varphi }{2}}}}={\frac {8}{3}}a\sin {\frac { \varphi }{2}}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93226b1c859be822160a3403fd366ef703eb1db4)







 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.